混凝土面板堆石坝中高趾墙结构应力计算分析

谢 浩，刘斯宏，王柳江，黄明坤，张 媛

（河海大学水工结构研究所，江苏 南京 210098）

0 前 言

混凝土面板堆石坝设计中，通常采用混凝土高趾墙的方式来弥补地形、地质条件的缺陷或处理与岸边相邻水工建筑物合理衔接问题[1]。SL228—2013《混凝土面板堆石坝设计规范》中定义趾墙为: “布置在趾板线上和面板连接的混凝土挡墙”，这表明高趾墙兼有趾板和挡土墙的双重作用。近年来，采用高趾墙的面板堆石坝工程不断增多，陆希等[2]通过材料力学法分析了公伯峡面板堆石坝高趾墙的应力状态及安全系数；沈振中等[3]采用三维非线性动力有限元方法，研究了海甸峡水电站面板堆石坝高趾墙的动力变形特性，论证了高趾墙在地震工况下的安全性；李振纲[4]以吉音水利枢纽工程为例通过三维有限元静动力分析表明了高趾墙作为非受力结构的垂直防渗体的可行性。本文采用材料力学法和三维整体有限元两种方法计算某工程高趾墙的结构应力，并对两种方法进行对比分析。

1 某工程高趾墙方案设计

某水电工程以发电为主，水库正常蓄水时上游水位340.0 m，下游水位260.0 m，最大坝高90.5 m，水库总库容5.42亿m3，电站装机容量230 MW，保证出力69.4 MW，多年平均发电量10.5858亿kW·h。工程枢纽主要由混凝土面板堆石坝、高趾墙、左岸岸坡式溢洪道、右岸泄洪排沙洞、引水发电系统及地面厂房等建筑物组成。

工程坝趾处河谷呈不对称 “V”形，左岸近河床存在宽100～140 m、坡角10°～15°的较平缓坡地，缓坡后山坡地形坡角30°～35°。右岸山坡地形坡角35°～45°。河谷底宽170 m～180 m，河床面高程263.00～271.00 m，设计正常蓄水位处河谷宽370～380 m。为了弥补趾板线地形、地质条件的缺陷并协调解决坝肩溢洪道的布置，本工程采用半重力式高趾墙。墙体总长172.5 m，最大墙高为62 m。高趾墙与坝体连接断面及剖面如图1所示，图中1-1、2-2、3-3分别对应墙后溢洪道的起始段、最高点和渐变段。

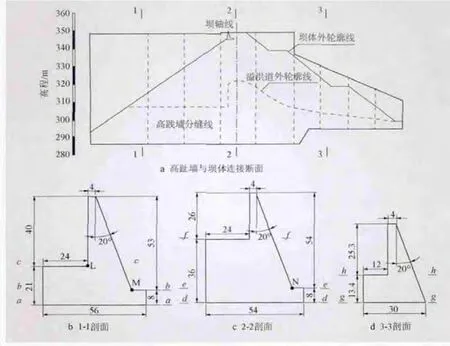
图1 高趾墙与坝体连接断面及剖面示意（单位:m）

2 材料力学法计算分析

本文对高趾墙的应力变形进行计算分析，计算工况与荷载见表1。

表1 计算工况与荷载

用材料力学法计算高趾墙的应力是一种常用的方法。其基本思想是假定高趾墙计算截面上的垂直正应力σz呈直线分布，通过平衡条件推算出墙体内任何一点的应力分量和主应力[5]，因此计算截面最大应力应位于左右两侧边缘，计算简图见图2。

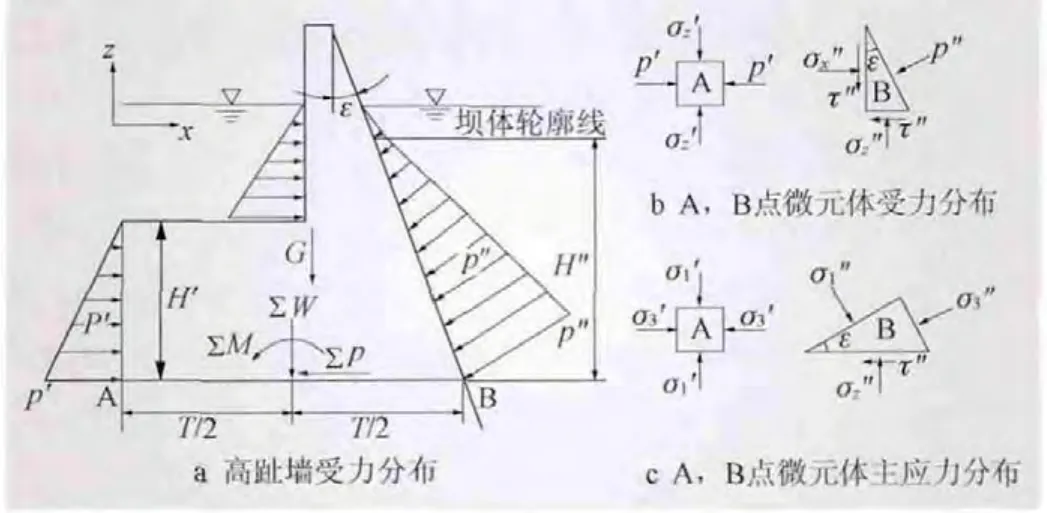
图2 高趾墙受力分析

由材料力学偏心受压公式可计算出左右边缘的竖向正应力。

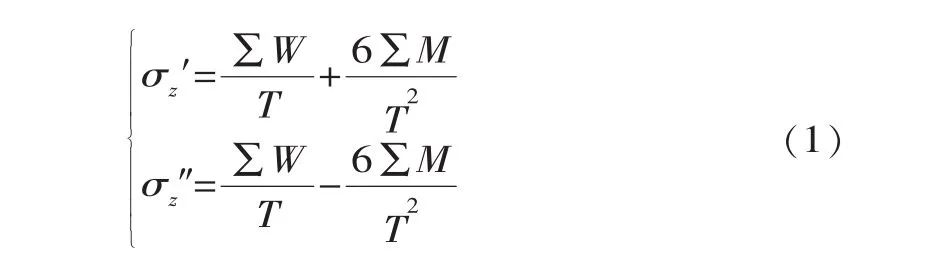
式中，σz′为左边缘A点竖向正应力；σz″为右边缘B点竖向正应力；ΣW为作用在计算截面以上全部荷载的铅直分力总和；ΣM为作用在计算截面以上全部荷载对截面形心的力矩总和；T为计算截面沿坝轴方向的宽度。

近似认为左右边界上所受的土压力垂直于高趾墙面，由材料力学法可知，主应力作用面上无剪应力，故左右趾墙面为主应力面之一。取图2b、2c所示的微元体，由作用在高趾墙面微元体上力的平衡条件ΣFz=0可得，边缘主应力为

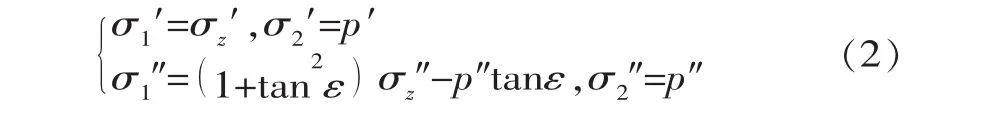
式中，p′为趾墙左边缘A点所受的土压力强度；p″为趾墙右边缘B点所受的土压力强度。

因面板堆石坝主要以无粘性的堆石为主，高趾墙又是一个刚性结构，故按照库伦土压力理论计算主动土压力[6-8]:

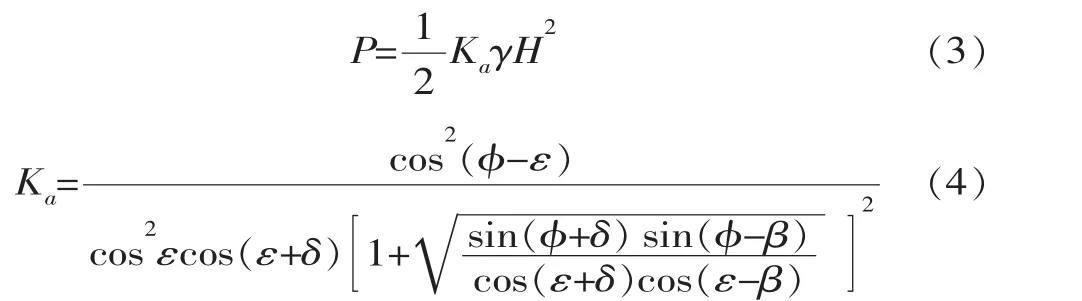
式中，Ka为主动土压力系数；γ、φ分别为填土的重度、内摩擦角；ε为墙背与铅直线的夹角；δ为墙摩擦角；β为填土表面与水平面的夹角。本文取堆石区 γ=20.9 kN/m3，φ=40°，δ=20°。 考虑最危险的截面，如图 1 中的 a-a、b-b、c-c、d-d、e-e、f-f、g-g、h-h共7个计算截面，边缘主应力计算结果如表2所示:

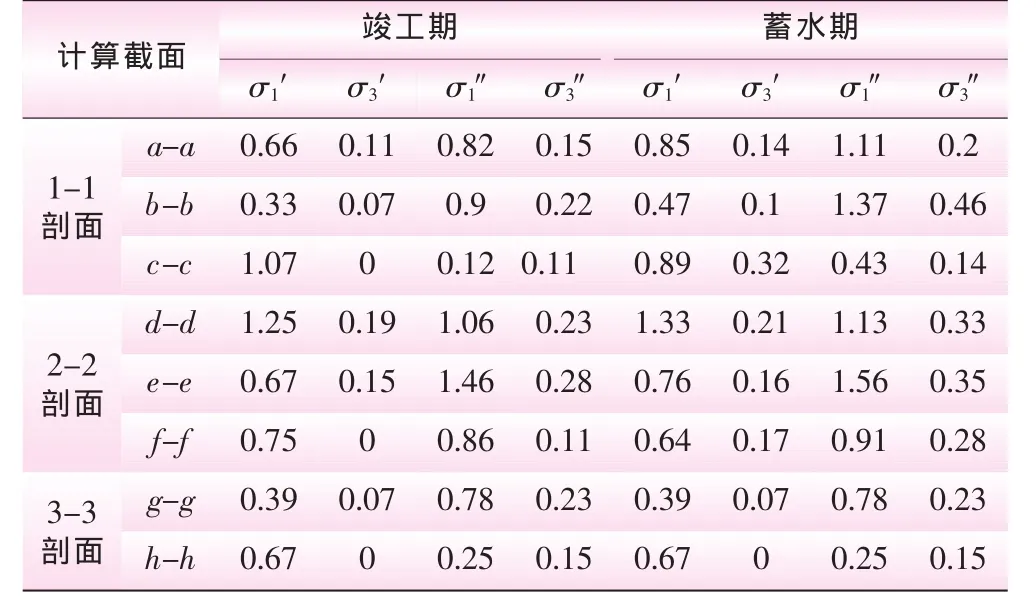
表2 边缘主应力计算结果（材料力学法）MPa

根据计算结果，竣工期和蓄水期最大主应力均位于2-2剖面的e-e截面右边缘，大小是1.46 MPa和1.56 MPa，由此可知，该处为整个高趾墙的最危险点。除趾墙底面大主应力超过1.0 MPa外，其余部位均在1.0 MPa以内，整个趾墙内没有出现拉应力区。蓄水期1-1、2-2剖面的各部位应力均较竣工期增加，而3-3剖面则与竣工期一致，这是因为蓄水期下游水位为260 m，低于高趾墙底面高程287 m。

3 有限元法计算分析

由于高趾墙垂直于坝轴线方向，材料力学法没有计入沿上下游方向承受的水压力，且无法考虑不同高趾墙墙体分块之间的相互作用。 《混凝土面板堆石坝设计规范》 中规定:“100 m以上的 1、2级高坝坝体应力和变形宜用有限元法计算”，故对高趾墙进行三维有限元计算分析。建立有限元模型如图3所示，共有21121个单元，23383个节点，其中高趾墙部分有2564单元，3295节点。模型材料参数见表3，其中土石材料本构关系采用邓肯E-B模型，强弱风化基岩和混凝土材料采用线弹性模型。

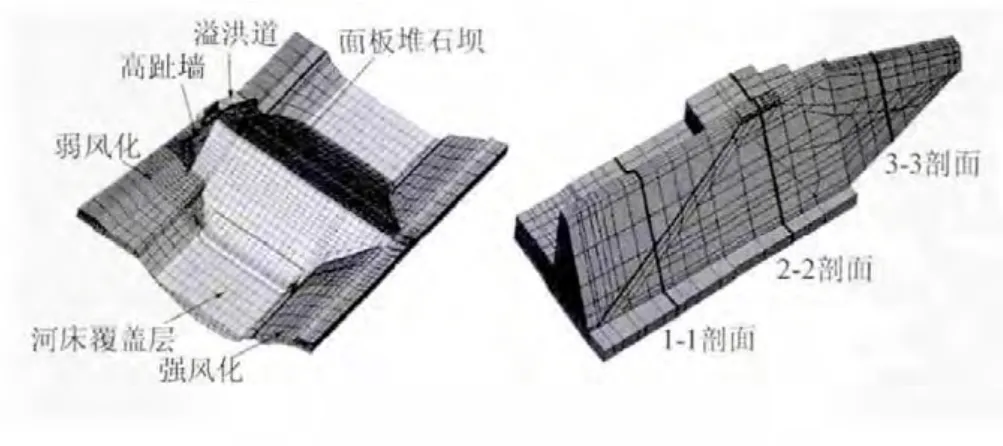
图3 三维有限元网格

施加荷载时，首先模拟天然坝基覆盖层求得初始应力，然后模拟高趾墙和溢洪道的浇筑，再按高程逐层分级填筑坝体，最后是面板，完全真实地模拟工程的施工顺序，以保证计算结果真实有效。有限元法高趾墙结构应力计算结果如表4所示。

根据计算结果可知，整体上无论是竣工期还是蓄水期，高趾墙底部的应力高于上部，但均不大于2 MPa，满足高趾墙混凝土的抗压强度；局部上，1-1、2-2剖面高趾墙与坝体相接面的底端转折处有少量的应力集中 （如图1b中的M点和图1c中的N点），是整个高趾墙的最大主应力分布点。对比两种工况的结果可知，高趾墙1-1剖面蓄水后受到水压力的作用，大主应力较竣工期增大，但也减小了cc截面左边缘的应力集中 （如图1b中的L点），这是由于蓄水后左侧水压力大于右侧水压力；2-2剖面竣工期下部的应力分布与蓄水期大致相似，只是蓄水期应力稍大；3-3剖面竣工期和蓄水期的应力分布情况基本一致。

4 材料力学法与有限元法的对比分析

图4为用有限元法计算的高趾墙大主应力分布，可知，用材料力学法和有限元法计算的高趾墙内大主应力分布大致相同，特点是:①最大主应力均位于高趾墙与坝体相接面的底端转折处；②类似于重力式挡土墙，高趾墙自上而下大主应力逐渐增大；由于坝体一侧土压力的作用，越深入坝体一侧，高趾墙底面的大主应力越大；③蓄水后高趾墙内各处大主应力均有不同程度的增加，但局部由于水压力的作用，应力集中现象得到缓和。

高趾墙内小主应力均在-0.5～0.5 MPa以内，在混凝土的抗拉强度以内，最小值均位于高趾墙顶端或左侧平台顶端。但两种方法的计算结果略有差异，材料力学法的结果表明趾墙内不存在拉应力区，而有限元法的小主应力最小值虽也位于同样的位置，但有较小的拉应力。这是因为材料力学法考虑的是平面应变问题，没有考虑上下游方向水荷载的影响，而小主应力的方向刚好较接近于上下游方向；另外，材料力学法假定计算截面上应力呈线性分布，而从有限元的结果来看，高趾墙下部1/4～1/3范围内并无此规律，故此假定并不完全成立。

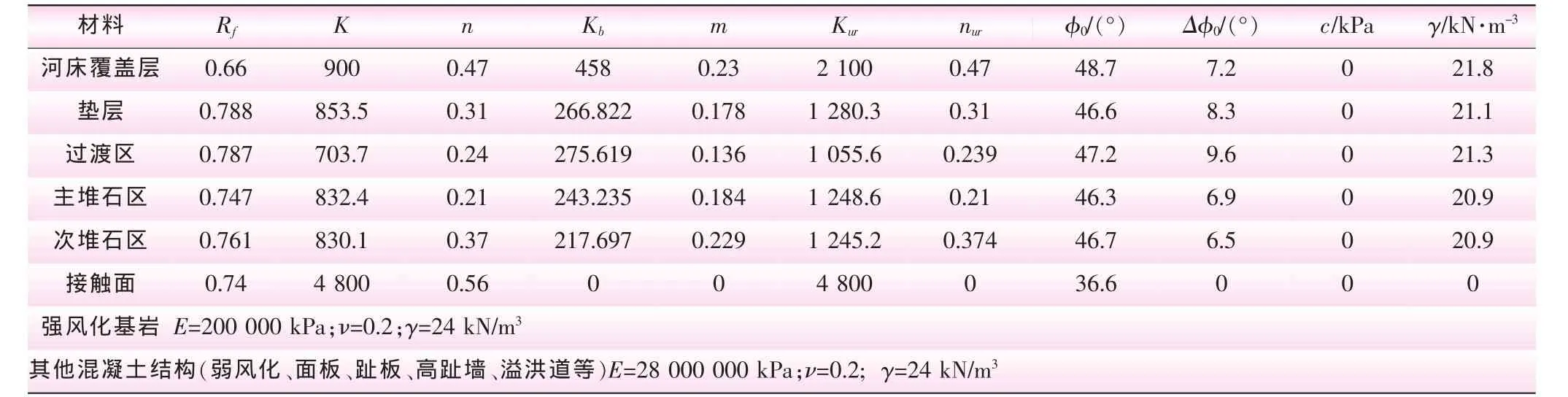
表3 材料参数

表4 边缘主应力计算结果（有限元法）MPa

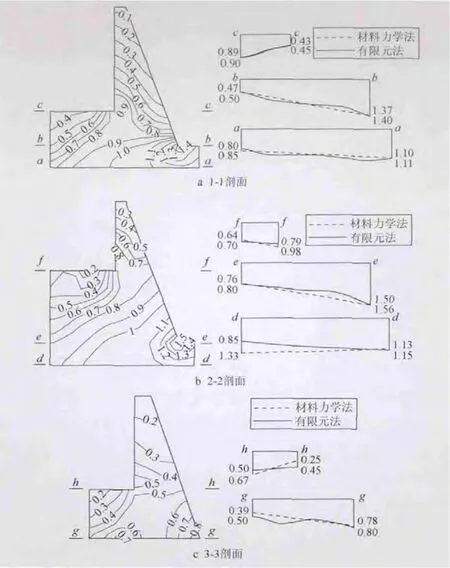
图4 蓄水期有限元计算结构大主应力分布及两种计算结果对比 （单位:kPa）

5 结论

本文对某混凝土面板堆石坝的高趾墙结构进行应力计算，通过采用材料力学法和有限元法对比分析可知:

（1）高趾墙的大主应力位于高趾墙与坝体相接面的底端转折处，该处存在轻微的应力集中现象，但最大应力不超过2 MPa，满足混凝土的抗压强度要求。

（2）高趾墙的顶端和左侧平台存在局部拉应力区，小主应力值在-0.5～0.5 MPa以内，满足混凝土的抗拉强度要求。

（3）材料力学法计算简便、快捷，得出的边缘大主应力值与有限元法接近，结构下部1/4～1/3以上应力分布规律与有限元法结果类似，表明高趾墙结构设计采用材料力学法计算可行，但由于存在平面问题的局限性，且无法考虑上下游水压力和高趾墙分块以及其他荷载影响，得出的小主应力不一定准确，故对重要工程应进一步用有限元法校核。

［1］安盛勋.混凝土面板堆石坝潜没式混凝土高趾墙设计［J］.西北水电，2009（2）:18-21.

［2］陆希，安盛勋，陈念水，等.公伯峡面板堆石坝右岸高趾墙设计［J］.水力发电，2004，30（8）:38-40.

［3］沈振中，迟世春，陈剑.混凝土面板堆石坝高趾墙动力性态计算研究［J］.水电能源科学，2005（2）:73-75.

［4］李振纲.吉音水利枢纽工程混凝土面板坝高趾墙设计 ［J］.水力发电，2011，37（10）:44-47.

［5］陈胜宏，陈敏林，赖国伟.水工建筑物 ［M］.北京:中国水利水电出版社，2004.

［6］侍倩.土力学［M］.武汉:武汉大学出版社，2004.

［7］SL 379—2007 水工挡土墙设计规范［S］.

［8］GB 50007—2002 建筑地基基础设计规范［S］.

［9］SL 228—2013 混凝土面板堆石坝设计规范［S］.