基于多元回归分析的大伙房水库径流中长期预报

王 琪，张亭亭，游海林，常 静，曹永强

（辽宁师范大学城市与环境学院，辽宁 大连 116029）

0 引 言

随着人口增长与社会发展，水资源已成为影响人类21世纪生存与发展的一个重要因素。正确及时的中长期水文预报[1]，能够使人们在解决防洪与抗旱、蓄水与弃水及各部门用水之间矛盾时及早采取措施进行统筹安排，并使综合效益达到最大化。因此，水文中长期预报在水资源合理配置与充分利用方面具有重要参考价值，积极开展其研究是非常有必要的。

目前，应用较广的中长期水文统计预报方法主要有多元分析与时间序列分析[2]。大量研究发现，在中长期水文预报中，关键预报因子的选择和优化是提高预报精度的关键[3-4]。大伙房水库[5]位于浑河中上游，抚顺市东部郊区，是一座集防洪、工业及城市供水、灌溉、发电、养鱼等综合利用项目的大型水利枢纽工程。大伙房水库控制流域面积5437 km3，总库容21.87×108m3。在缓解浑太地区水资源供需矛盾、提供辽宁省中部地区工业与生活用水及环境用水、解决该地区工农业用水短缺问题上，具有重要作用[6]。

因此，本文依据预报因子选取原则和相关物理机制，筛选出10个大伙房水库年径流的影响因子，采用主成分分析法和Logistic方程多元回归法，拟建立中长期预报模型，并进行外推检验以探究其预报精度，力争为该水库防洪、灌溉、发电、供水提供有价值的参考依据。

1 研究方法简介

回归分析是水文预报中最常用的方法之一，其主要思路是:分析影响预报因子的各种因素，依据一定的规则，选择其中一个或几个重要的因素作为影响因子，搜集预报因子与影响因子的历史资料，并按此资料确定含参数的关系解析式，采用优化方法求解参数，利用模型进行预测[7-8]。

水文预报的影响因子众多，本文采用主成分回归方法，该方法是在不损失或减少损失原有信息的前提下，将原来多个彼此相关的指标转换成新的少数几个彼此独立的综合指标，体现降维思想[9]。径流预报总是受限于一定自然条件和社会经济、技术水平，在整个时间进程，呈阻尼增长。鉴于此特点，可以近似用生态学中的Logistic曲线来描述径流预报的变化过程。

2 多元回归预报模型构建

2.1 主成分推求

根据预报因子的选取原则[10-12]、物理考察[13-14]和统计分析[15]，本文最终选取10项大伙房年径流影响因子。即，x1为当年1月太阳黑子数；x2为前一年年平均太阳黑子数；x3为前一年东太平洋副高面积指数；x4为前一年11、12月东太平洋副高强度指数；x5为前一年年平均南方涛动值；x6为前一年亚洲极涡强度指数；x7为前一年西太平洋年均海温；x8为沈阳700 hPa当年2月19日时位势高；x9为当年4月入库径流量；x10为前一年降水量。基于1956年～2000年 （共计45a）10项统计数据资料，应用SPSS统计分析软件[16]进行主成分分析，求出相关矩阵的特征根λ、单个因子的方差贡献率e及累计方差贡献率E （见表1）。

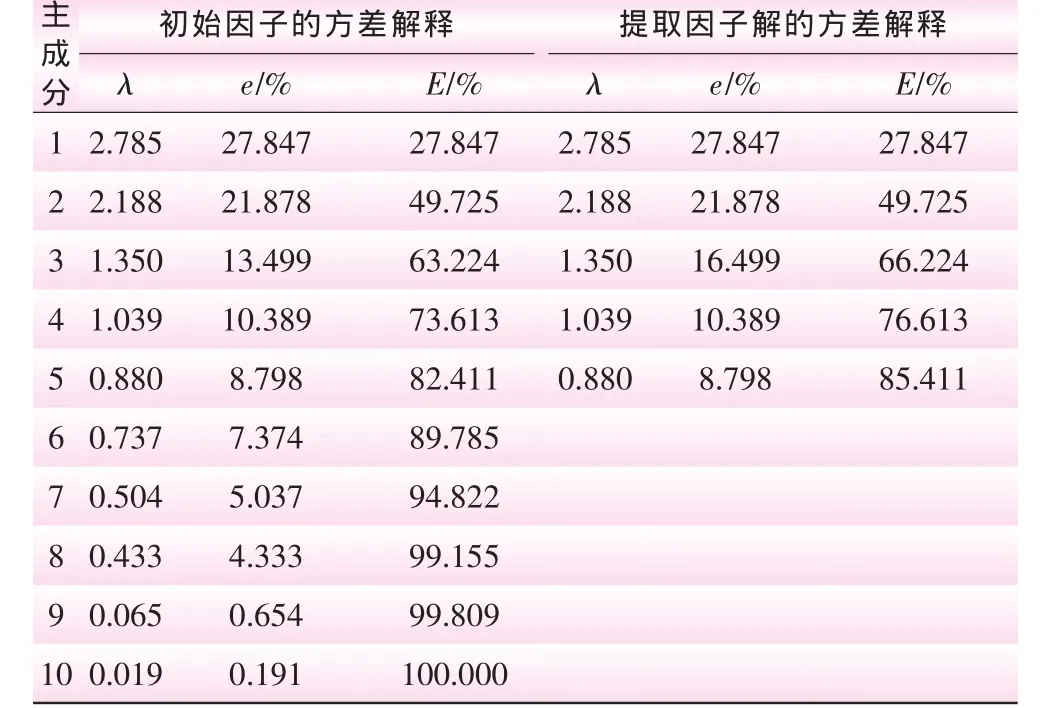
表1 因子分析解释总变量

由表1可知，第一个因子的特征根λ1=2.785，解释10个原始变量总方差的27.847%，累计方差贡献率为27.847%；第二个因子特征根λ2=2.188，解释10个原始变量总方差的21.878%，累计方差贡献率为49.725%；依次类推。第二部分提取因子解的方差解释描述了提取后的因子对总方差的解释情况。这里根据取累计方差贡献率大于等于85%的原则确定提取因子的个数。由表1可以得到，λ1=2.785，λ2=2.188，λ3=1.350，λ4=1.039，λ5=0.880，E=e1+e2+e3+e4+e5=85.411%。也就是说，5个因子共解释10个原始变量总方差的85.411%，大于85%，能够较好地解释总体情况，故取提取因子数k=5。表2为利用回归法估计的因子得分系数。

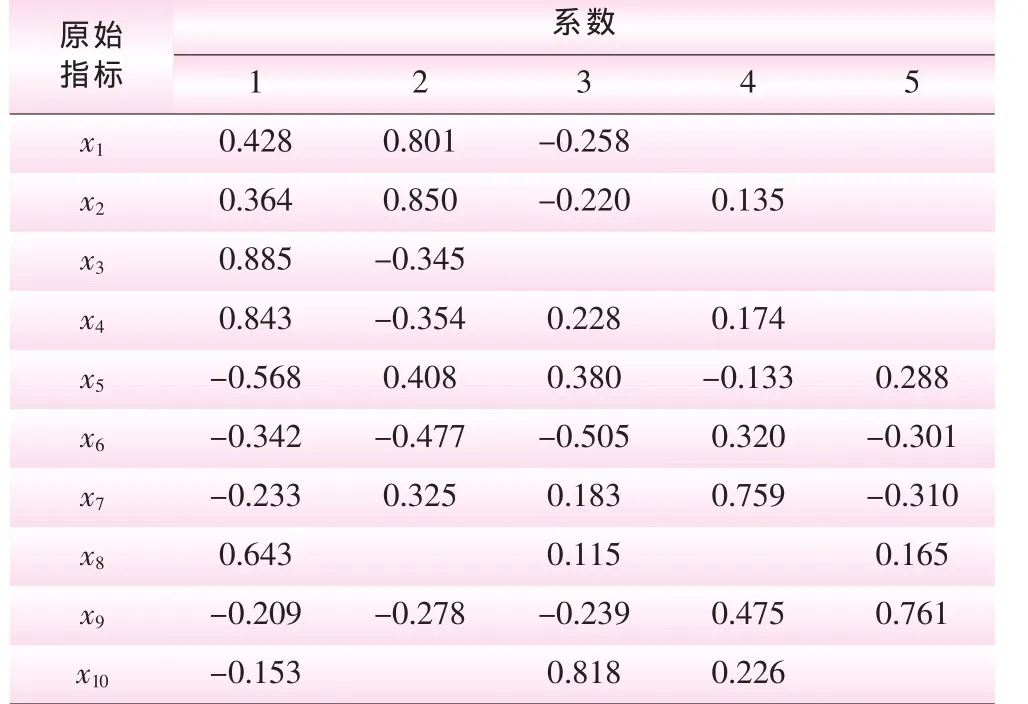
表2 因子得分的系数矩阵

由表2可知，10个原始指标 （x1，…，x10）与前5个主成分 （综合因子z1、z2、z3、z4、z5）的关系

2.2 综合因子的Logistic方程拟合

应用SPSS统计分析软件对综合因子z～z5的计算值用logistic曲线[17-20]拟合（t为时间），求得；

2.3 模型的构建

对大伙房年径流量 （Y）及综合因子z进行多元线性回归分析，得到模型回归系数 （如表3）。

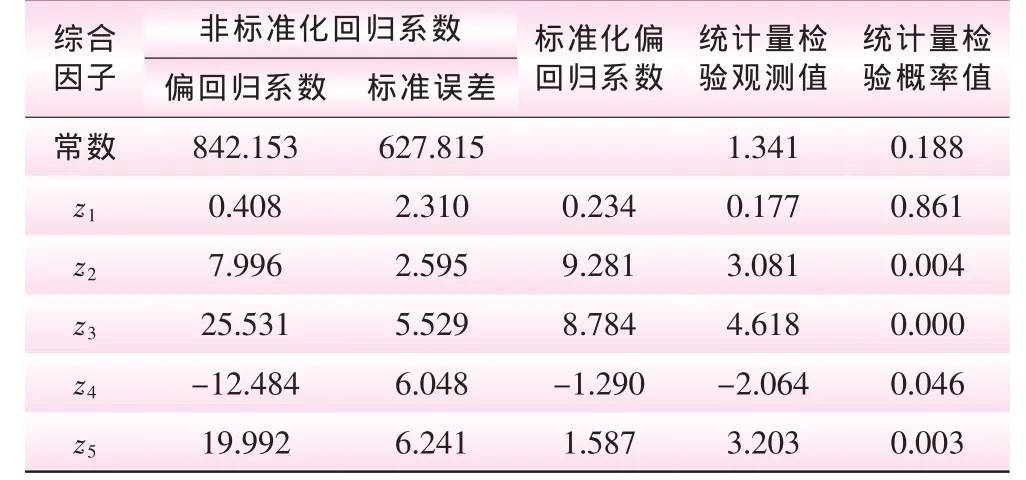
表3 回归系数

建立如下多元回归模型:Y=842.153+0.408z1+7.996z2+25.531z3-12.484z4+19.992z5。

3 预报模型的检验

为了对回归效果进行定量判断，拟对回归效果进行检验。本文采用复相关系数法[19，21]对回归效果进行检验，最终得复相关系数值R=0.815，证明回归效果是显著的。

对样本年限内的年径流量进行预报拟合，基于主成分分析和Logistic方程多元回归模型的大伙房水库预报模型对大伙房水库年径流量的拟合情况较好。大伙房水库径流模拟相对误差计算结果见表4。

从表4可以看出，年径流模拟值与实际值之间的相对误差在小于等于允许误差20%的年份有29年，占总年份的64.4%。根据SL 250—2000《水文情报预报规范》，预报精度等级达到丙级，预报精度较好，参考SL 250—2000中的精度评定标准认为该模型可以用于参考性预报。

4 结 论

（1）基于预报因子的选取原则、物理考察和统计分析，本文最终选取10项大伙房年径流影响因子。在此基础上，本文采用主成分分析法将10项影响因子转换成5个彼此独立的新的综合指标，从而减少变量数量，抓住主要矛盾，简化变量之间的关系，使原有指标获得综合的方差信息。此外，由于径流预报总是受限于一定的自然条件和社会经济技术水平，因此在整个时间进程中，其变化往往呈现阻尼增长。针对这一特征，本文选用生态学中的Logistic曲线来近似描述径流预报的变化过程，从而建立基于主成分分析和Logistic方程多元回归方法的大伙房水库径流中长期预报模型。

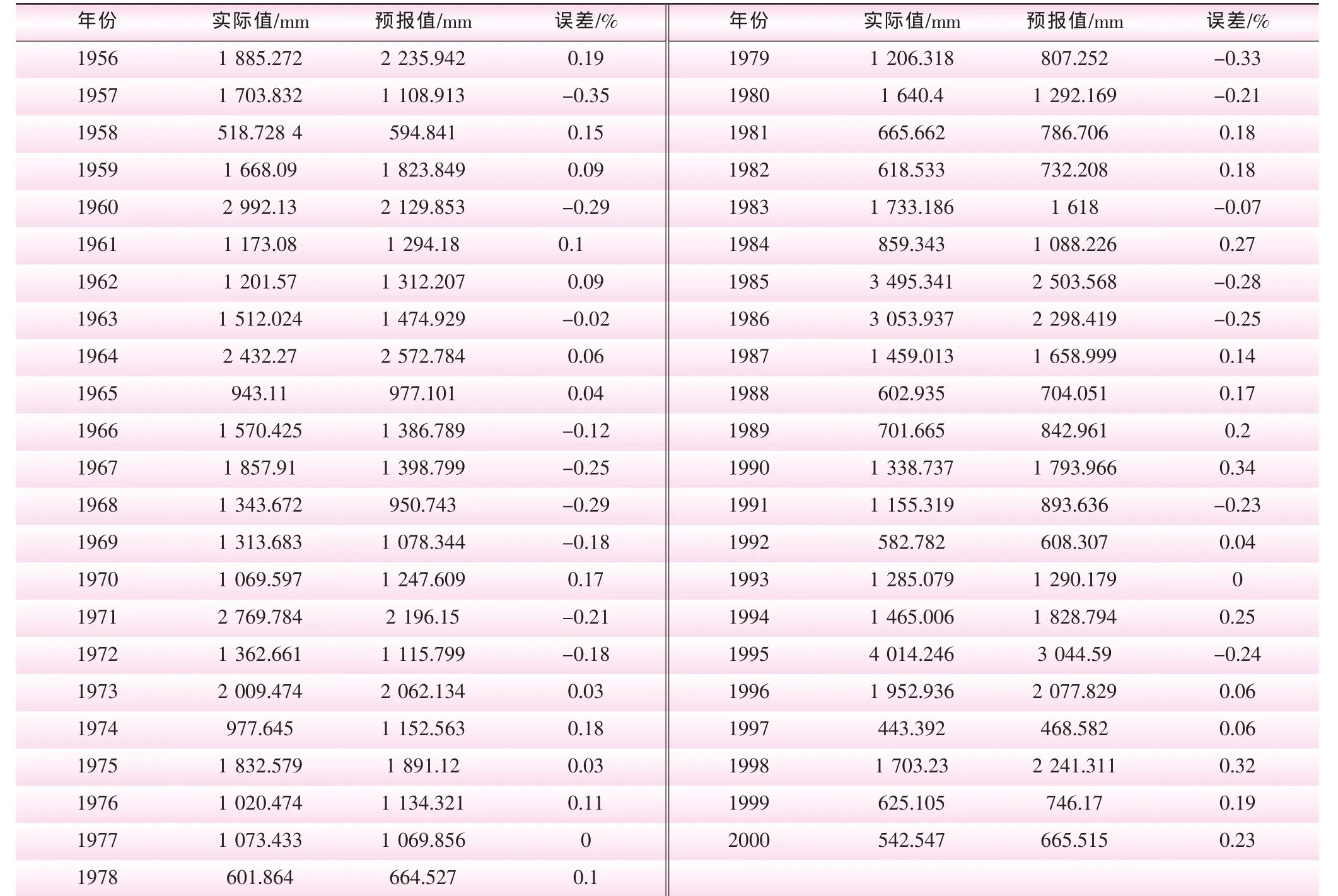
表4 大伙房水库径流模拟相对误差计算

（2）建立的大伙房水库径流中长期预报模型的拟合结果表明，该模型具有较高的精确度，可以较好地预测大伙房水库2000年之后的径流量。

［1］李博，李克锋，王莉.嘉陵江中游段中长期径流预报研究［J］.水力发电，2011，37（8）:7-10.

［2］杨旭，栾继河，冯国章.中长期水文预报研究评述与展望［J］.西北农业大学学报，2000，28（6）:103-207.

［3］朱之葵，王峨生，李慰如.模糊数学法在水库长期径流预报中的应用［J］.水力发电，1993（4）:15-19.

［4］冯小冲.水库中长期水文预报模型研究［D］.南京:南京水利科学研究院，2010.

［5］辽宁省大伙房水库管理局.大伙房水库调度工作手册［M］.抚顺:辽宁省大伙房水库管理局，2008.

［6］董艳萍.大伙房径流中长期预报及引水调度方式研究［D］.大连:大连理工大学，2008.

［7］姚宜斌，陶本藻，施闯.稳健回归分析及其应用研究［J］.大地测量与地球动力学，2002，22（2）:16-19.

［8］王志良，邱林，梁川，等.作物需水量与气温关系的模糊回归分析［J］.华北水利水电学院学报，2001，22（4）:4-6.

［9］徐建华.计量地理学［M］.北京:高等教育出版社，2006:95-100.

［10］汤成友，官学文，张世明.现代中长期水文预报方法及其应用［M］.北京:中国水利水电出版社，2008.

［11］王本德.水文中长期预报模糊数学方法［J］.大连:大连理工大学出版社，1992.

［12］游海林.大伙房水库径流中长期预报方法应用研究［D］.大连:辽宁师范大学，2010.

［13］汤成友，官学文，张世明.现代中长期水文预报方法及其应用［M］.北京:中国水利水电出版社，2008.

［14］孙树青.长江三峡中长期水文预报研究［D］.湖南:长沙理工大学,2007.

［15］张丽霞.新疆塔城地区农九师中小河流中长期预报问题的研究［D］.乌鲁木齐:新疆农业大学，2006.

［16］薛薇.基于SPSS的数据分析［M］.北京:中国人民大学出版社，2006:283-284.

［17］姜永，李德新.Logistic方程的灰色建模法 ［J］.福建农林大学学报: 自然科版，2004，12（4）:535-537.

［18］Menon A,Bhandarkar S.Predicting polymorphic transformation curves using a logistic equation ［J］.International Journal of Pharmaceutics,2004,286（1/2）:125-129.

［19］Jensen A L Simple density-dependent matrix model forpopulation projection［J］.Ecological Modeling,1995,77（1）:43-48.

［20］Sadkowski A.On the application of the logistic differential equation in electrochemical dynamics［J］.Journal of Electroanalytical Chemistry,2000,486（1）:92-94.

［21］叶守泽，詹道江.工程水文学［M］.北京:中国水利水电出版社，2000.