例谈2013年高考物理卷对科学方法的考查

吴 强

（山东省泰山中学，山东 泰安 271000）

随着新课程的改革和新课程高考的推进，新课程高考出现了“突出主干、体现方法、回归经典、强化能力”的特点.尤其是2013年高考更加突出了对科学方法的考查，下面笔者对2013年高考中出现的以物理科学方法为载体的考题进行分析.以期对2014年备考的广大师生有所助益.

1 2013年全国新课标卷对科学方法的考查

2013年全国新课标卷Ⅰ，突出了对理想化方法、对称法、等效法、图像法的考查；2013年全国新课标卷Ⅱ，突出了对理想化方法、对称法、等效法、图像法、临界法、假设法、隔离法的考查.具体情况，可分别见表1和表2.

表1

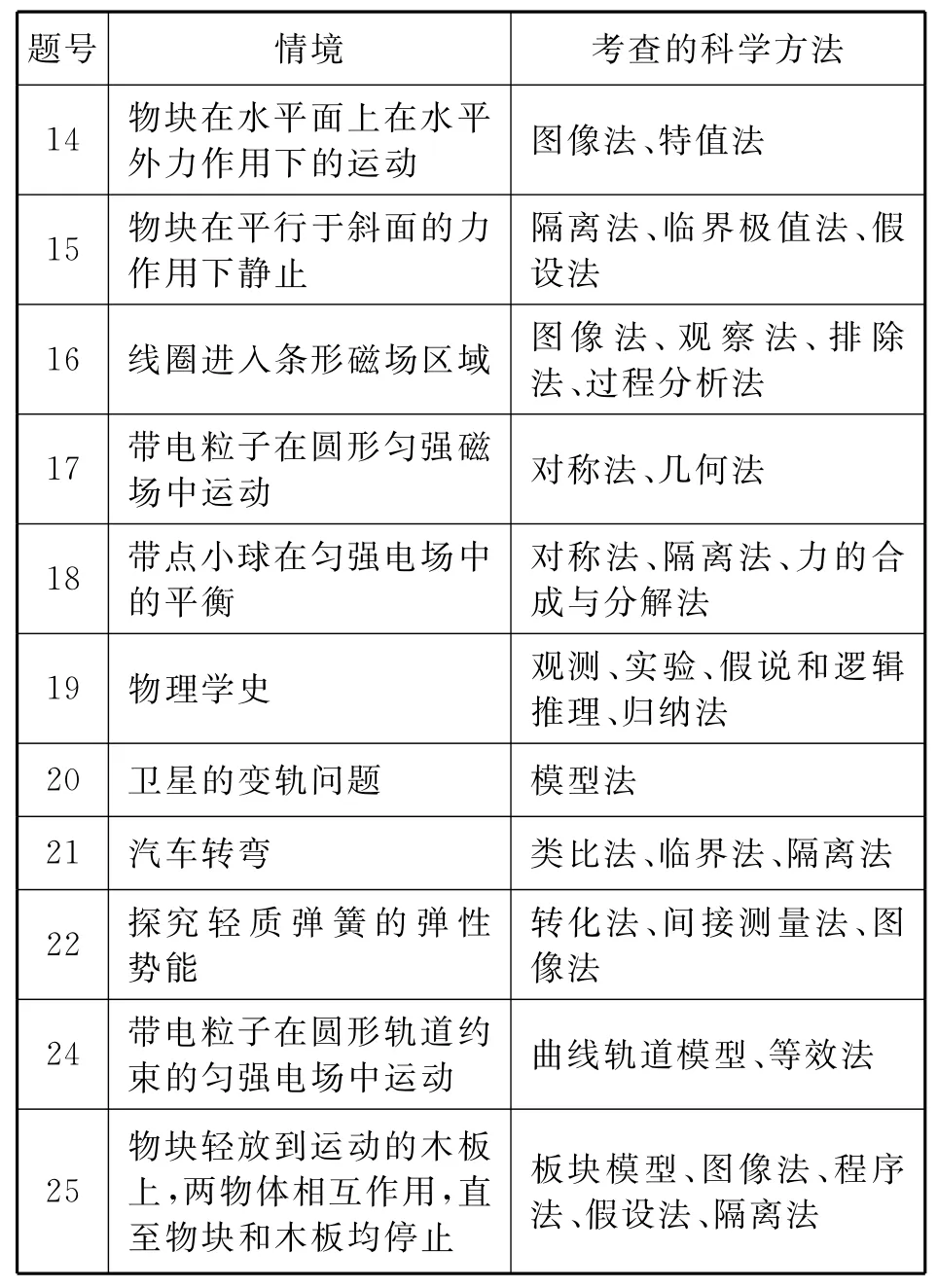
表2

2 对试题中科学方法考查的剖析

2.1 极限法

所谓极限分析法，就是把问题推到极端状态下或特殊状态下进行分析的方法，关键是考虑将问题推向什么极端，即应选择变量，所选择的变量要在变化过程中存在极值或临界值，然后从极大和极小或极左和极右的极端状态出发，分析问题的变化规律，并依此做出科学的推理分析，从而给出判断或导出一般结论，实现问题解决.

图1

例1.（2013年山东卷第22题）如图1所示，一质量m＝0.4kg的小物块，以v0＝2m／s的初速度，在与斜面成某一角度的拉力F作用下，沿斜面向上做匀加速运动，经t＝2s的时间物块由A点运动到E点，A、E两点间的距离L＝10m.已知斜面倾角θ＝30°，物块与斜面之间的动摩擦因数，重力加速度g取10m／s2.

（1）求物块加速度的大小及到达E点时速度的大小.

（2）拉力F与斜面夹角多大时，拉力F最小？拉力F的最小值是多少？

解析：（1）设物块加速度的大小为a，到达E点时速度的大小为v，由运动学公式得

联立（1）、（2）式得

a＝3m／s2. （3）

v＝8m／s. （4）

（2）物块在斜面向上做匀加速直线运动，若假设加速度为零，则系统处于平衡状态.则此时，物块在4个力作用下做匀速直线运动.

如图2所示，同一接触面的弹力与摩擦力方向相互垂直，当动摩擦因数μ不变时，弹力FN与摩擦力Ff的合力F'的方向与FN的夹角为β＝arctanμ.当弹力FN增大或减小时，摩擦力Ff也按比例增大或减小，两力的合力大小增大或减小但其方向不变.

图2

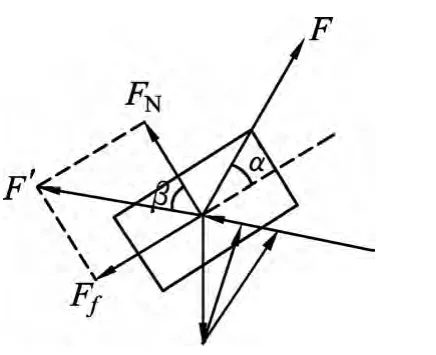
图3

图4

物体受重力、拉力F及弹力FN和摩擦力Ff的合力F'作用下平衡，如图3所示.设F与斜面方向的夹角为α，则α＝β＝arctanμ＝30°时，拉力F最小.

设物块所受支持力为FN，所受摩擦力为Ff，拉力与斜面间的夹角为α，受力分析如图4所示，由牛顿第二定律得

联立（5）～（7）式得

点评：本题设置了单一物体的单一过程问题，考查了匀加速直线运动的基本规律和求解动力学问题的基本方法.解决本题采用了极小值的方法，令加速度变化到最小为0，则转化为平衡态，利用弹力和滑动摩擦力的特点，将4力平衡问题转化为3力平衡问题，利用图解法迅速得到出现极小值的条件，还考查了极限法、转化法、图解法、正交分解法.解决本题也可以选择常规方法，在受多个力的情况下，以运动方向建立直角坐标系，应用正交分解法求出所求量的表达式，再利用数学方法求得极值.

2.2 对称法

对称法就是根据某些物理情境中的几何图形、物理现象、物理规律、物理过程的对称性进行命题、解题的一种科学方法.一般来说利用对称法解题可以按如下步骤进行.

（1）审视物理情境，选取研究对象.在仔细审题的基础上，选取恰当的研究对象，如运动的物体、运动的某一过程或某一状态.通过题目的背景、条件、设问，深刻剖析物理现象及过程，建立清晰的物理情境.

（2）缜密分析研究对象的性质（包括图形、图像以及所处的物理环境，如接触面情况，场的分布等等），运动特点（包括运动轨迹、运动过程）及规律（包括过程规律、状态规律以及前后过程和状态间的联系等等）.

（3）寻找研究对象的对称性特点，在已有经验的基础上通过直觉思维，或借助对称原理的启发进行联想类比，来分析挖掘研究对象在某些属性上或运动过程、规律的变化上的对称性.这是解题的关键环节.

（4）利用对称性的特点，依据物理规律列方程，求解得出物理结果.

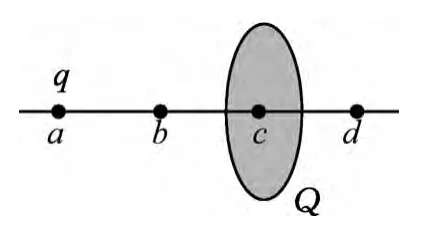
图5

例2.（2013年新课标卷Ⅰ第15题）如图5所示，一半径为R的圆盘上均匀分布着电荷量为Q的电荷，在垂直于圆盘且过圆心c的轴线上有a、b、d3个点，a和b、b和c、c和d间的距离均为R，在a点处有一电荷量为q的固定点电荷.已知b点处的场强为零，则d点处场强的大小为（k为静电力常量）

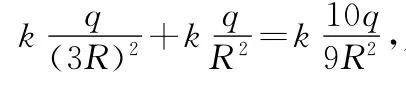
点评：本题考查了点电荷的场强的计算方法和场强的叠加原理.带电圆盘在其对称点b、d两点处产生的电场强度大小相等方向相反.这里以关于面的对称性命题，利用了对称法来解决问题.

2.3 微元法

微元法是指人们在处理问题时，将其研究对象或物理过程分解为若干微小的“元对象”或“元过程”，由于每个“元对象”或“元过程”遵循相同的规律，所以只需分析某个“元对象”或“元过程”，然后再将“元对象”或“元过程”进行必要的数学方法或物理思想处理，进而使问题求解的符合科学思维方法.

“微元法”作为高中物理的一个重要思想方法，在应用于处理物理问题时，其解题思路可概括为：① 选取微元用以量化元研究对象或元研究过程；② 视元研究对象或元研究过程为恒定，运用相应的规律给出待求量对应的微元表达式；③ 在微元表达式的定义域内给以叠加演算，进而求得待求量.选取“微元”，将瞬时变化问题转化为平均变化或恒定不变的问题，再利用数学中的“微积分”知识，将平均变化或恒定不变的问题转化为瞬时变化问题，这样实现了化繁为简，顺利地解决问题.

图6

例3.（2013 年 新 课标Ⅰ卷第25题）如图6所示，两条平行导轨所在平面与水平地面的夹角为θ，间距为L.导轨上端接有一平行板电容器，电容为C.导轨处于匀强磁场中，磁感应强度大小为E.方向垂直于导轨平面.在导轨上放置质量为m的金属棒，棒可沿导轨下滑，且在下滑过程中保持与导轨垂直并良好接触.已知金属棒与导轨之间的动摩擦因数为μ，重力加速度大小为g.忽略所有电阻，让金属棒从导轨上端由静止开始下滑，求：

（1）电容器极板上积累的电荷量与金属棒速度大小的关系；

（2）金属棒的速度大小随时间变化的关系.

解析：（1）设金属棒下滑的速度大小为v，则感应电动势为

平行板电容器两极板之间的电势差为

设此时电容器极板上积累的电荷量为Q，按定义有

联立（1）～（3）式得

（2）设金属棒的速度大小为v时经历的时间为t，通过金属棒的电流为i.金属棒受到的磁场的作用力方向沿导轨向上，大小为

设在时间间隔（t，t＋Δt）内流经金属棒的电荷量为ΔQ，则按定义有

ΔQ也是平行板电容器在时间间隔（t，t＋Δt）内增加的电荷量.由（4）式得

式中，Δv为金属棒的速度变化量.按定义有

而金属棒所受到的摩擦力方向斜向上，大小为

式中，N是金属棒对于导轨的正压力的大小，有

金属棒在时刻t的加速度方向沿斜面向下，设其大小为a，根据牛顿第二定律有

联立（5）～（11）式得

由（12）式及题设可知，金属棒做初速度为零的匀加速运动.t时刻金属棒的速度大小为

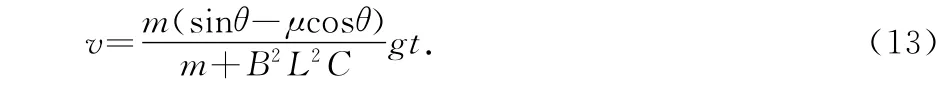
点评：导体棒做切割磁感线运动，导体棒等效为电源给电容器充电，利用微元法选取导体棒运动过程中某一元过程为研究对象，证明导体棒做的是初速度为零的匀加速直线运动，进而得到金属棒的速度大小随时间变化的关系.考查了电磁感应与动力学结合的综合问题，考查了考生的分析受力、运动、电路、过程的能力以及综合解决问题的能力.

2.4 控制变量法

控制变量法就是在研究多因素的问题时，把多因素的问题转化成多个单因素的问题.每次只改变其中的某一个因素，而控制其余几个因素不变，从而研究被改变的这个因素对事物的影响，然后分别加以研究最后再综合实现问题解决的方法.

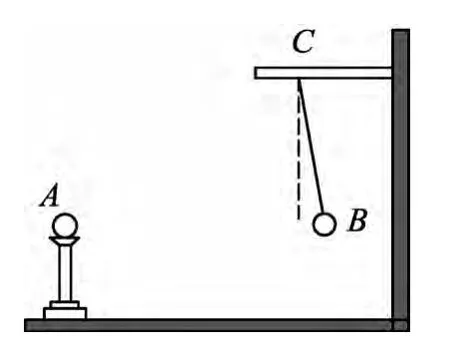
图7

例4.［2013年高考四川理综卷第8题（1）］在探究两电荷间相互作用力的大小与哪些因素有关的实验中，一学生猜想可能与两电荷的间距和带电荷量有关.他选用带正电的小球A和E，A球放在可移动的底座上，E球用绝缘丝线悬挂于玻璃棒C点，如图7所示.

实验时，先保持两电荷量不变，使A球从远处逐渐向E球靠近，观察到两球距离越小，E球悬线的偏角越大；再保持两球的距离不变，改变小球所带的电荷量，观察到电荷量越大，E球悬线的偏角越大.

实验表明，两电荷之间的相互作用力，随其距离的__________而增大，随其所带电荷量______________而增大.此学生在探究中应用的科学方法是__________（选填：“累积法”、“等效替代法”、“控制变量法”、“或演绎法”）

答案：减小；增大；控制变量法.

点评：本题考查了教科书中的演示实验，通过控制变量法来研究两电荷间相互作用力的大小与哪些因素有关，教科书中验证牛顿运动定律、探究电阻定律、探究单摆的运动测重力加速度等实验中都用到了控制变量法.

2.5 转化法

转化方法是问题解决的一种常见的、重要的策略方法，它蕴含着极其丰富的内容，如新旧知识间的转化，研究对象间的转化，未知向已知的转化，特殊与一般的转化，曲线运动向直线运动之间的转化等等.

在物理量的测量中，有些特征、过程或物理量的直接观测难以实现，这时可以把所要观测的变量转化成容易间接观察和测量的物理量，常用的转化方式有以下几种.

（1）物理量间的转化.把不易测量的量转化为容易测量的量.

（2）能量之间的转化.从一种形式转化为另一种形式或从一个物体转移到另一个物体上，在转化或转移的过程中能量的总量保持不变.

（3）动量之间的转化.从一个物体转移到另一个物体上，在转移的过程中动量的总量保持不变.

（4）图线之间的转化.两个物理量间的关系有很多不是一次函数关系，若直接以这两个物理量为坐标轴，所画出的图像不是直线，这样不利于发现这两个物理量间的关系，为此，通过物理量转化将图像由曲线转化为直线.

例5.（2013年全国新课标理综Ⅱ卷第22题）某学生利用下述装置对轻质弹簧的弹性势能进行探究：一轻质弹簧放置在光滑水平桌面上，弹簧左端固定，右端与一小球接触而不固连；弹簧处于原长时，小球恰好桌面边缘，如图8（a）所示.向左推小球，使弹簧压缩一段距离后由静止释放；小球离开桌面后落到水平地面.通过测量和计算.可求得弹簧被压缩后的弹性势能.回答下列问题：

图8

（1）本实验中可认为，弹簧被压缩后的弹性势能Ep与小球抛出时的动能Ek相等.已知重力加速度大小为g.为求得Ek，至少需要测量下列物理量中的（填正确答案标号）.

（A）小球的质量.

（B）小球抛出点到落地点的水平距离s.

（C）桌面到地面的高度h.

（D）弹簧的压缩量Δx.

（E）弹簧原长l0.

（2）用所选取的测量量和已知量表示Ek，得Ek＝

解析：要探究弹簧的弹性势能，依据题目的设置，弹簧的弹性势能先转化为小球抛出时的动能，为了计算小球的动能应转化为测量小球的质量和小球抛出时的初速度，要测小球抛出时的初速度，应转化为测小球做平抛运动的高度和水平距离.

（1）根据小球的动能表达式和平抛运动规律，得小球抛出时的动能根据平抛运动规律有h＝?解得?.故需要测量小球的质量m、小球抛出点到落地点的水平距离s和桌面到地面的高度h，选项（A）、（B）、（C）正确.

（2）见上述（1）中的解析.

（3）由图像可知，s与Δx成正比，设图像斜率为k，则s＝kΔx，弹性势能Ep与动能Ek的关系为故，即弹簧的弹性势能与Δx的二次方成正比.当h不变时，m增大，k就减小；当m不变时，h增大，k就增大.

点评：在探究弹簧的弹性势能的实验中利用了3次转化才达到了目的，首先转化为测量小球抛出时的动能，然后转化为测量小球的质量和抛出时的速度，最后转化为测小球做平抛运动的高度和水平距离.通过转化把难以测量的物理量转化为易于测量的物理量，还考查了利用数学方法处理物理问题的能力.

在高考命题中，考查物理科学方法已成为必然，常规的物理科学方法有，如观察实验、比较分类、分析综合、归纳演绎、理想化、类比、假说、数学方法等等.这些方法属程序性知识，认知心理学家指出，陈述性知识必须和程序性知识相结合，才能形成分析问题和解决问题的能力.因此，这就要求教师在平常的教学中，除了要把知识讲解透彻，更要关注物理学的科学方法.只有做到知识与方法的并进、统一，将科学方法自然、流畅、显性地呈现给学生，才能在物理教学过程中培养学生的能力，更好地落实新课程的三维目标.

1 张宪魁.物理科学方法因素判定原理［J］.物理教师，2012（11）：1-2.