“Wf＝－μmgl”全程等效意义及应用

帅厚梅 李庆国

（江苏省扬州市新华中学，江苏 扬州 225009）

在对物理过程的分析过程中，我们可以总结出一些结论或规律，这些结论或规律具有一定的普遍性和灵活应用性，若将其应用到相关问题中，可以使解题更为方便、快捷.下面笔者就对“Wf＝-μmgl”这一结论进行分析讨论，呈现其等效意义及在解题中的应用.

1 对Wf＝－μmgl的证明

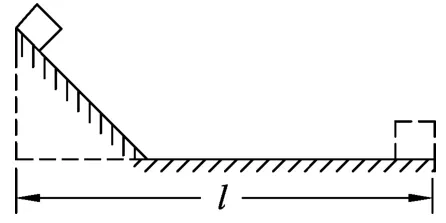
图1

如图1所示，一个质量为m的物体沿斜面滑下，并紧接着在水平面上滑行一段距离，测得初末位置间的水平位移为l，斜面与水平面对物体的动摩擦因数相同都为μ，重力加速度为g，不考虑物体滑至斜面底端的碰撞作用，可以证明这一运动过程中滑动摩擦力所做的功为Wf＝-μmgl.

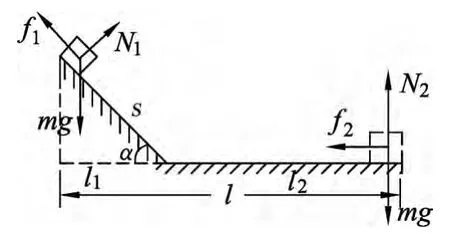
图2

证明：如图2所示，设斜面的夹角为α，斜面的长度为s，物体沿斜面运动所对应的水平位移为l1，物体沿水平面运动的位移为l2.物体沿斜面运动的过程中所受滑动摩擦力f1的大小为f1＝μN1＝μmgcosα，f1做的功W1为W1＝-f1s＝-μmgscosα＝-μmgl1.物体沿水平面运动的过程中所受滑动摩擦力f2的大小为f2＝μN2＝μmg，f2做的功W2为W2＝-f2l2＝-μmgl2.整个过程中，滑动摩擦力做的总功为W＝W1＋W2＝-μmg（l1＋l2）＝-μmgl.

2 对Wf＝－μmgl的理解

（1）成立条件：物体在垂直接触面上只受支持力和重力（或重力垂直于接触面的分力），若物体在平行于接触面方向上除摩擦力外还受其他力，结论仍然成立.

（2）l的含义：起点与终点的水平距离，不是物体通过的路程.即滑动摩擦力所做的功与斜面的倾角无关，而与整个运动过程中所对应水平位移有关.

（3）μmg的含义：不是物体在斜面上运动时滑动摩擦力的大小，因为物体在斜面上运动时滑动摩擦力为μmgcosα，并且当倾角变化时摩擦力也会随之变化.μmg可以看作是物体在水平面上运动时滑动摩擦力的大小.

图3

（4）等效：物体在全程中滑动摩擦力所做的功，从效果上看，相当于物体在长为l的水平面上运动过程中滑动摩擦力所做的功.即可以将图2全程中滑动摩擦力所做的功等效成物体在水平面上运动相同水平位移时滑动摩擦力所做的功，如图3所示.只要全程所对应的水平位移相同，则全程滑动摩擦力所做的功相同.

3 对Wf＝－μmgl的应用

下面笔者通过几道典型例题来对Wf＝-μmgl这一结论进行具体应用.

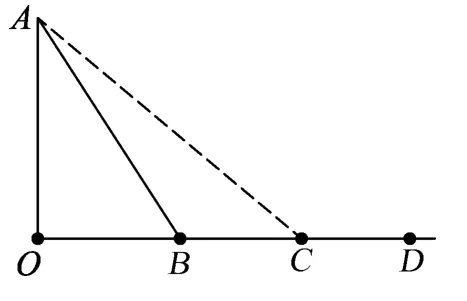
图4

例1.如图4所示，OD是一水平面，AE为一斜面，一质点由A点静止释放，沿斜面AE滑下，最后停在D点，不考虑物体滑至斜面底端的碰撞作用，若斜面改为AC（仅倾角变化），仍从A点由静止释放，则最终停在水平面OD上的（设物体与斜面间的动摩擦因数处处相等）

（A）D点右侧. （B）D点左侧.

（C）D点. （D）无法确定.

解析：若用动能定理求解，则沿两种斜面运动过程中重力所做的功相同，关键是求滑动摩擦力所做的功.斜面倾角发生变化、斜面上的滑动摩擦力发生变化、斜面长度发生变化、水平面长度发生变化.既有斜面上的运动，又有水平面上的运动，还得分段写方程，需要设定的未知量比较多，这些令许多学生“望而生畏”.若利用Wf＝-μmgl这一结论，求全程滑动摩擦力所做的功相当于求物体在OD水平面上运动相同水平位移时滑动摩擦力所做的功，则可使解题思路变得较为简单、清晰.

设A点的竖直高度为h，质点从斜面AE由静止滑下停在D点，所对应的水平位移为l1，则根据动能定理和Wf＝-μmgl这一结论可得mgh-μmgl1＝0-0（A点和D点的速度为0，即初末位置的动能为0）.若质点从斜面AC由静止滑下至最终停下来，设所对应的水平位移为l2，则有mgh-μmgl1＝0-0.比较两个方程可知l1＝l2，即质点最终仍然停在水平面上的D点，正确选项为（C）.

变式：如图4所示，物体以初速度v0，从D点出发沿DEA滑到顶点A点时速度恰好为0.若斜面改为AC，让该物体从D点出发沿DCA滑到顶点A点时速度也恰好为0，则物体具有的初速度为（设物体与路面间的动摩擦因数处处相等且不为0）

（A）大于v0. （B）等于v0.

（C）小于v0. （D）取决于斜面的倾角.

解析：变式与例1是类似的，若利用Wf＝-μmgl这一结论可以简化解题过程，提高解题效率.设A点的竖直高度为h，物体从D点出发沿DEA滑到顶点A，所对应的水平位移为l，则根据动能定理和Wf＝-μmgl这一结论可得-mgh-μmgl＝0-.若物体从D点出发沿DCA滑到顶点A，其所对应的水平位移仍为l，设初速度为v，则有-mgh-μmgl＝0-比较两个方程式可知v＝v0，正确选项为（B）.

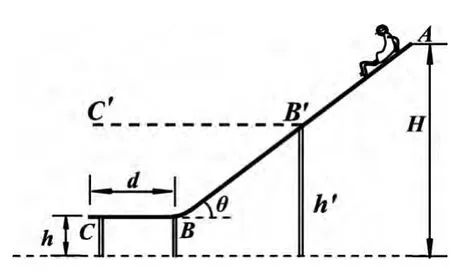
图5

例2.水上滑梯可简化成如图5所示的模型：倾角为θ＝37°斜滑道AE和水平滑道EC平滑连接，起点A距水面的高度H＝7.0m，EC长d＝2.0m，端点C距水面的高度h＝1.0m.一质量m＝50kg的运动员从滑道起点A点无初速地自由滑下，运动员与AE、EC间的动摩擦因数均为μ＝0.10.（取重力加速度g＝10m／s2，cos37°＝0.8，sin37°＝0.6，运动员在运动过程中可视为质点）.

（1）求运动员沿AE下滑时加速度的大小a；

（2）求运动员从A滑到C的过程中克服摩擦力所做的功W和到达C点时速度的大小v；

（3）保持水平滑道端点在同一竖直线上，调节水平滑道高度h和长度d到图中E'C'位置时，运动员从滑梯平抛到水面的水平位移最大，求此时滑道E'C'距水面的高度h'.

解析：（1）a＝gsinθ-μgcosθ＝5.2m／s2.

对于第（2）问，用常规方法需要分段求摩擦力所做的功，列式过程比较麻烦，而根据Wf＝-μmgl这一结论可知，运动员从A滑到C的过程中克服摩擦力所做的功W为W＝μmg（＋d） ＝500J，一个方程即可解决问题.再根据动能定理有mg（H-h）-W＝mv2-0，可得v＝10m／s.

对于第（3）问，要表示出运动员从滑梯平抛到水面的水平位移，则必须先表示出运动员到达C点的速度.根据教学经验，多数学生都能想到用动能定理求到达C点的速度，但就是对求“保持水平滑道端点在同一竖直线上，调节水平滑道高度h和长度d”这一过程中滑动摩擦力所做的功感到“束手无策”，因为学生感到这一变化过程得分段进行分析，而每一段的位移又在发生变化，表示起来比较麻烦，从而导致此问求不出来.若利用Wf＝-μmgl这一结论，滑动摩擦力所做的功只与水平位移有关，由题目中“保持水平滑道端点在同一竖直线上”可知，调节水平滑道高度h和长度d并不影响运动员在整个滑道上所对应的水平位移，因此在整个滑道上运动过程中克服摩擦力所做的功仍为第（2）问所求的W.则根据动能定理可以求出C点的速度为

图6

例3.如图6所示，一个滑雪运动员从左侧斜坡距离坡底竖直高度H1＝8m的高处由静止自由滑下，以坡底为零势能参考面，当下滑到距离坡底h1高处时，运动员的动能和势能恰好相等，到坡底后运动员又靠惯性冲上右侧斜坡，当上滑到距离坡底h2高处时，运动员的动能和势能再次相等，最后上滑的最大高度H2＝4m，全程运动员通过的水平距离为l＝20m，运动员与斜坡间的动摩擦因数处处相等，不计经过坡底时的机械能损失.在此过程中，下列说法正确的是

（A）h1＜4m，h2＞2m.

（B）滑雪板与雪面的动摩擦因数为0.2.

（C）滑雪运动员到达右侧最高处后可能不再返回.

（D）滑雪运动员从右侧返回再次冲上左侧斜坡的最大高度为2m.

解析：本题正确选项为（A）、（B），可以证明滑雪运动员到达右侧最高处后能够返回，这里重点讨论（B）、（D）两个选项.运动员从左侧斜坡由静止下滑运动至右侧斜坡的最大高度处，这一过程中，根据动能定理和Wf＝-μmgl这一结论即可得mg（H1-H2）-μmgl＝0-0.由此得μ＝代入数据得μ＝0.2，因此（B）选项正确.

考虑到Wf＝-μmgl这一结论，全程中滑动摩擦力所做的功可等效成物体在水平面上运动相同水平位移时滑动摩擦力所做的功.因此，如图7所示，运动员从A处（H＝8m处）无论沿倾角多大的斜面滑下，都能上滑到E处（H＝4m处）且速度为0.即此运动员可以沿着如图7所示的ACE、ADE、AEE等不同路径运动，重力和滑动摩擦力所做的功都相同.假设运动员沿着不同的路径返回到达左侧斜坡H3＝2m高处（如图中粗虚线所示高度），重力所做的功相同，而运动所对应的水平位移并不相同，即这一返回过程中滑动摩擦力所做的功并不相同，根据动能定理可知，运动员到达左侧斜坡H3＝2m高处的速度并不相同，即滑雪运动员从右侧返回再次冲上左侧斜坡的最大高度并不一定为2m（若α＞θ则到达不了2m高度，若α＜θ能到达2m高度以上，若α＝θ刚好到达2m高度）.因此（D）选项不正确.若不用Wf＝-μmgl这一结论，则很难通过列方程来判断（D）选项的正误.

在高中物理中经常会出现涉及斜面与平面相结合的题目，而且往往会涉及到滑动摩擦力做功，如果教师在教学过程中能够引导学生灵活运用Wf＝-μmgl这一结论，无疑可以拓宽学生的解题思路，简化解题过程，提高解题速度，从而提高学生的物理成绩.

其实，只要在平时教学过程中多思考、多分析、多总结，就会发现有许多像“Wf＝-μmgl”这一类书本上没有但又很实用的结论，例如，“平抛运动速度的反向延长线与水平位移的交点为水平位移的中点”、“不计重力带电粒子沿着半径方向射入圆形磁场必沿着半径方向射出圆形磁场”等等.充分、灵活应用这些结论，可以提高教师的教学效率及学生的学习效率，使“教与学”达到“事半功倍”的效果.