基于重力辅助导航误差分析的自适应介入匹配算法

文超斌，王跃钢，郭志斌，田 琦，左朝阳，滕红磊

（1. 第二炮兵工程大学，304教研室，西安 710025；2. 中国人民解放军96124部队，通化 134000）

基于重力辅助导航误差分析的自适应介入匹配算法

文超斌1,2，王跃钢1，郭志斌1，田 琦1，左朝阳1，滕红磊1

（1. 第二炮兵工程大学，304教研室，西安 710025；2. 中国人民解放军96124部队，通化 134000）

针对现有重力导航匹配算法受测量误差和非测量误差影响匹配精度、匹配率较低而导致实践应用困难的不足，通过理论分析算法误差源，提出了一种自适应介入匹配算法。该算法通过判断等值点的特征空间特性以及最近距离和阀值的关系，对惯导位置参数进行自适应修正，极大提高了算法匹配率、搜索效率、实时性的效果。仿真实验结果表明，经自适应处理，可使算法最优匹配率达到89.6%，定位误差保持在500～700 m，重力图分辨率(1')降至25%左右。

重力辅助导航; 高斯样条插值; 重力误差补偿; 导航模型

现有海洋重力异常场分辨率已经达到2′×2′，进一步插值精细化处理可达1′×1′，海洋重力仪的测量精度达到1 mGal，这给较高精度重力辅助导航提供了可能性[1]。重力匹配基本思路就是通过某种匹配策略实现由惯性导航系统指示的导航系统位置到导航系统真实位置的最优逼近，按照算法设计原理可分为序列相关匹配方法和递推滤波方法两种，序列相关匹配方法主要包括最近等值线迭代算法（ICCP），相关极值分析算法两大类[2-4]，经过近几年的发展各类匹配算法获得了巨大的发展。但针对各类匹配算法匹配误差和误匹配成因的分析并不多，并且由于测量误差和非测量误差的影响重力匹配算法总存在误差[5-9]，这样在利用匹配算法获得匹配参数后就要通过相应的方法来判断该估计参数的精度、有效性，进而判断匹配参数是否可以用来修正惯导参数，避免盲目修正，关于这一方面的研究较少。所以，本文建立了重力辅助导航算法误匹配产生的理论模型，探究了误匹配产生的本质原因，给出了相应的理论说明，提出了一种自适介入匹配算法。该算法自适应决定重力辅助导航模块是否介入惯性导航系统，从而最终提高重力辅助惯性导航算法的定位计算误差。

1 重力辅助导航误差分析

1.1 理论建模

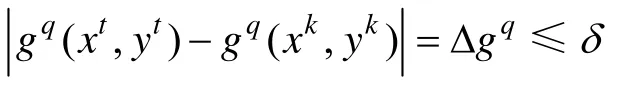
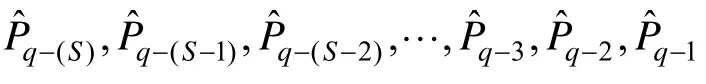
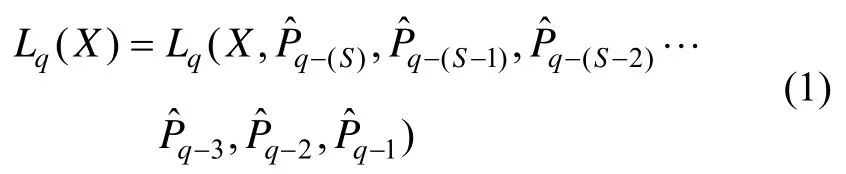
为书写方便上式简记为：

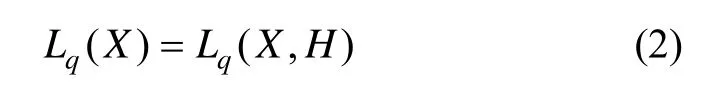
用H表示： Pˆq-(S),P ˆq-(S-1), P ˆq-(S-2),…,Pˆq-3,Pˆq-2,Pˆq-1。这样连续重力参考图 的任意点 依据式(2)可映射为空间中的一个点，同时定义 RKq为重力辅助匹配算法的特征空间。如前述定义和公理1所述，Φqc中任意点与参考图子图 Xqiq的距离，依相似性度可定义为式(3)：

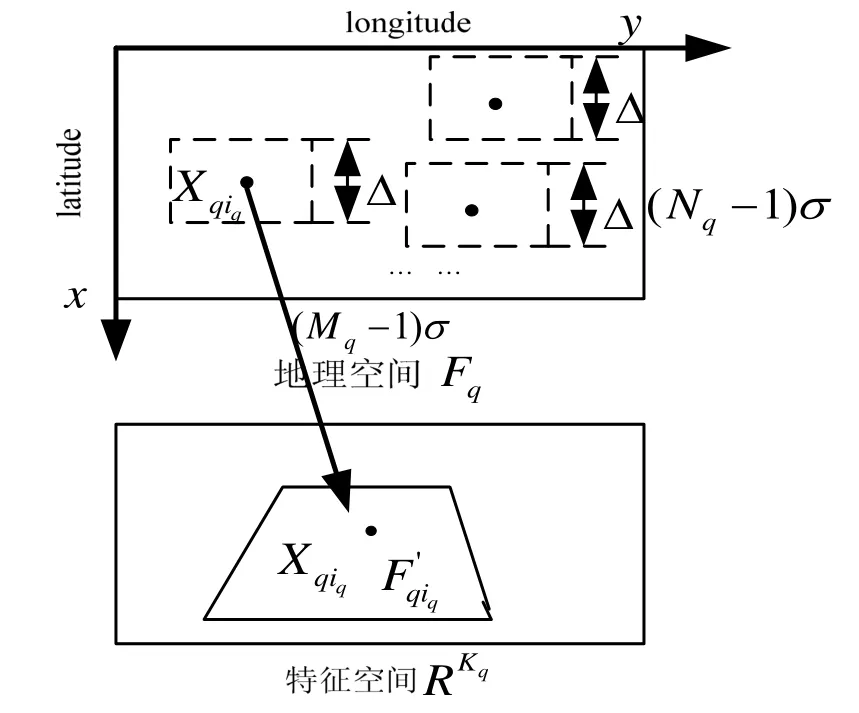
图1 地理空间映射为特征空间示意图Fig.1 Area in geographical space is mapped to feature space

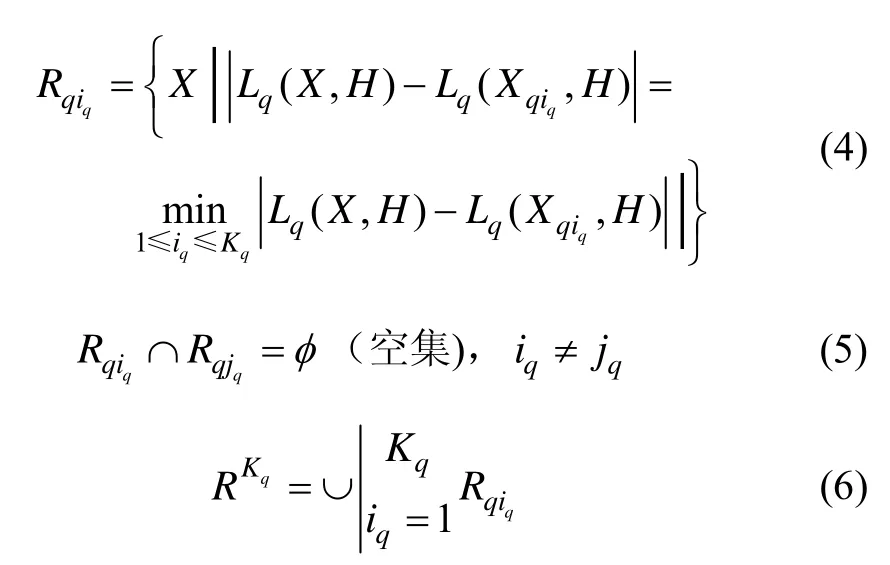
若第q个惯导系统给出的未校正测量点 Pq∈ Rqiq，则匹配算法会判定 Xr= Xqiq。这样，重力辅助导航匹配算法可以统一看成是通过确定实时图在特征空间中的位置来确定在地理空间 Fq中的位置的过程。

1.2 无测量误差情况

如图1示，设工程实践中重力匹配算法经、纬度绝对误差超过Δ(根据具体的应用背景对匹配精度的要求确定)时认为误匹配结果不可用，在地理空间 Fq中分别以参考图子图 Xq1,Xq2,…,Xq(Kq-1),XqKq为中心，以Δ为边长，作矩形 Fqiq，称 Fqiq为 Xqiq的邻域，且：

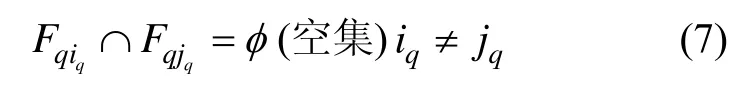
① 真实位置点 Xr∈ Fqiq，若有：

则一定有 Xr= Xqiq，此时 Xqiq距离 Fq的边界为0.5Δ，系统匹配误差为0.5Δ。

② 真实位置点 Xr∈ Fqiq，若有：

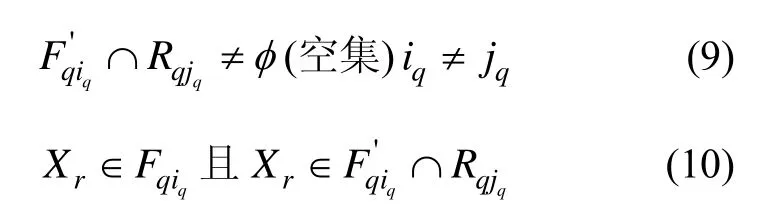
匹配算法可能会误判定 Pq= Xqjq，此时 Xqiq距离 Fq的边界为0.5Δ系统匹配误差大于0.5Δ。以上这样的误匹配是在实时图没有测量误差的条件下出现的，定义为非测量误差引起的误差，该误差是由匹配算法计算过程、求解方法、运算手段、适配区域的重力图数字特性引起的[10]。

1.3 有测量误差情况

实际重力测量值和载体真实位置点对应的实际重力值总存在测量误差，称实际重力值计算得到的等值点按定义1所述对应的参考图为 Xqiq(iq= 1,2… Kq)，同样离散参考图区域 Φqd内按照同样准则确定了个等值点，称 Φqd中的个等值点为参考图的子图，记为(iq= 1,2,… ,)。

重力测量误差足够大时对真实位置点 Xr∈ Fqiq，利用带有测量误差的重力值进行计算辨识载体的真实位置∈，且与 Xqiq的距离大于误差Δ时这样肯定会出现测量误差引起的误匹配。以上这样的误匹配定义为测量误差引起的，该误差是由重力实时测量数据的垂直扰动误差补偿技术、水平加速度扰动、厄特弗斯效应、由于补偿产生的二级畸变误差，以及为了将测量数据和重力图数据统一到一个平面而进行的延拓、递归误差引起的[12]。

2 重力辅助导航自适应介入算法

2.1 自适应介入原理

设第q个由惯导系统给出的未经校正测量位置点Pq对应的经过重力辅助导航匹配后的估计点为，在地理空间中寻找与对应的等值点参考子图记为Xqiq，根据重力辅助匹配算法的基本原理有= Xqiq， Xqiq在特征空间 RKq中的判决域为 Rqiq；在地理空间 Fq中的邻域为 Fqiq， Fqiq映射为 RKq中的超曲面：

① 由1.2节关于无重力测量误差情况下误差产生的原因分析可知若有：

则不会出现无重力测量误差情况下的误匹配。

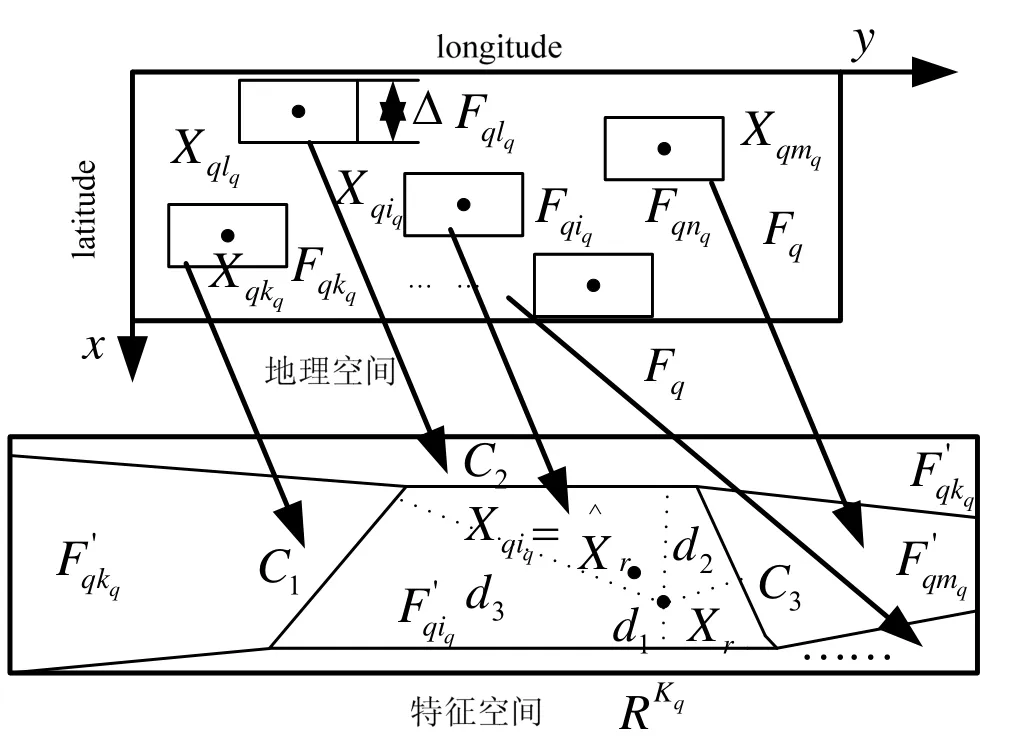
图2 测量误差引起误匹配示意图Fig.2 Mismatch caused by measure errors

则有：

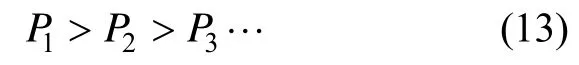
故载体的真实位置 Xr跨越分界面 C1,C2,C3…的概率主要取决于 P1。而 P1的值取决于 d1， d1越大跨越的可能性就越小，d1越小跨越的可能性就越大。同时结合式(11)知，若真实位置 Xr跨越分界面 C1,C2,C3…，利用带有测量误差的重力值进行计算估计值与真实位置点 Xr将属于不同的特征子空间，这样会出现测量误差引起的误匹配。所以说 d1越大跨越的误匹配可能性就越小， d1越小跨越的误匹配可能性就越大。

由此可依照式(3)，定义式(14)为等值点参考子图Xqiq的最近距离 d1，利用最近距离 d1可定量的反应误匹配发生的定性特征，同时刻画出由于测量误差引起误匹配的程度，进而可通过数值实验得到式(14)确定的最近距离 d1与匹配概率之间的关系曲线；然后将重力辅助导航完全匹配时对应的最近距离最小值作为最近距离的阈值，利用该阈值就可自适应确定重力辅助匹配算法是否介入惯性导航。

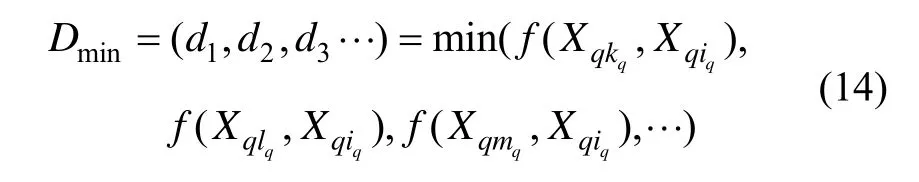
2.2 自适应介入算法流程

依据上述重力导航算法自适应介入原理可知重力辅助匹配算法自适应介入算法的流程如下叙述：

① 利用正常重力辅助算法计算得到重力辅助导航中第q个由惯导系统给出的未经校正测量位置点 Pq对应的经过重力辅助导航匹配后的测量位置点。

③ 求出 Xqiq在特征空间 RKq中的判决域 Rqiq，Xqiq在地理空间 Fq中的邻域 Fqiq映射为 RKq中的超曲面。判断与 Rqiq的关系，若⊂ Rqjq则转④，否则 q = q+1转①；

④ 寻找 Xqiq周围（绕其一周）距离等值点参考子图Xqiq最近的等值点参考子图 Xqkq,Xqlq,Xqmq…，利用式(14)计算等值点参考子图 Xqiq与周围子图 Xqkq, Xqlq,Xqmq,…,的最小距离 Dmin，当 Dmin＞ Γ时转⑤，否则 q = q+1转①；

上述参数Γ 为重力辅助导航算法具体重力测量误差情况下，为使特定匹配导航算法达到相应的匹配误差而通过实验得到的最小距离 Dmin的阈值，可根据重力测量误差的界限情况，通过实验得到最短距离 Dmin与匹配概率之间的关系曲线；然后按照实际应用对匹配概率的要求确定阈值Γ。

3 仿真试验与分析

本文采用第二炮兵工程大学惯性导航实验室基于MATLAB软件自行开发研制的惯性导航轨迹生成软件生成仿真需要的真实航迹和惯导指示航迹，其中重力异常数据使用经度范围118°～119°，纬度范围37°～38°的真实数据，该重力异常场的三维图如图3所示。重力图分辨率为1'×1'，对于经度,纬度计算误差超过一个重力图分辨率的情况即认为是误匹配[13]；惯导指示航迹的误差源有惯导初始位置误差、常值漂移和随机噪声 3种，初始位置误差为 0.01°，常值漂移误差为0.01 (°)/h；随机噪声为均值为0，标准差为0.001 (°)/h的高斯分布白噪声，按照3.2节所示重力辅助导航算法自适应介入流程进行匹配计算。重力仪的实时量测数据是利用真实航迹在重力数据库中的采样值分别叠加0.4 mGal、0.6 mGal、0.8 mGal的随机量测噪声获取。本文首先在上述重力测量误差情况下，分别针对自适应相关极值和自适应ICCP重力辅助导航匹配算法，研究得到了最短距离 Dmin与匹配概率之间的关系曲线，然后对比分析了典型相关极值和ICCP重力辅助导航匹配算法在本文所述自适应规则引入前后算法的匹配率和经纬度误差变化情况。

任取图3所示重力异常场中的50个点作为载体起始位置，由惯性导航轨迹生成器软件生成仿真需要的50组真实航迹和惯导指示航迹，而后在阈值Γ分别为10 m, 20 m, 30 m, …, 300 m，利用本文2.4节所述的自适应相关极值和自适应ICCP重力辅助导航算法对惯导指示航迹进行修正，得到如图4所示最短阈值和与匹配概率的关系曲线。曲线表明匹配概率伴随着最近距离Γ的增大而增大，在Γ =250 m以后本文叙述的两类自适算法匹配概率大于80%。

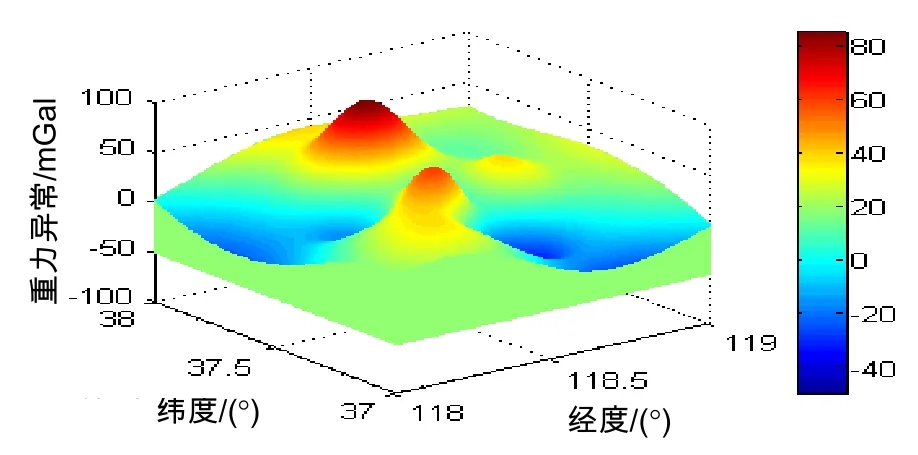
图3 重力异常场三维图Fig.3 3D map of gravity anomaly field

为了进一步分析本文自适应匹配算法的效能，在阈值Γ =227 m的情况下，表1给出了自适应机理引入前后50组重力辅助匹配导航数据匹配概率以及平均误差的统计结果。分析表格数据可知，当取阈值Γ =227 m时，自适应重力辅助算法比原来传统算法的匹配概率大幅度提高，测量平均误差变为原来的1/4到1/2左右，相关极值和ICCP算法在重力测量噪声为0.4 MGal时经纬度最优匹配率分别为85.3%和89.6%；平均误差分别为527 m和496 m。可见：由于匹配算法的自适处理可使算法能够保持在0.004°～0.006°(约500～700 m)左右的经纬度误差值，因此可将惯导配率提高了近30%，经纬度误差降至重力图分辨率1'(0.016°)的25%左右。

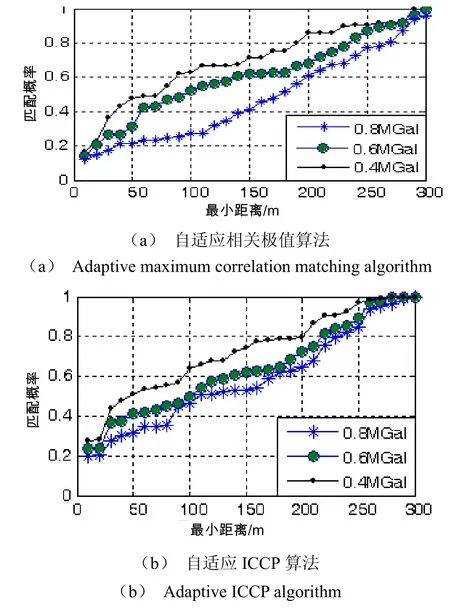
图4 最近距离阀值与匹配概率的关系曲线Fig.4 Relationship curve between proximate distance and matching probability

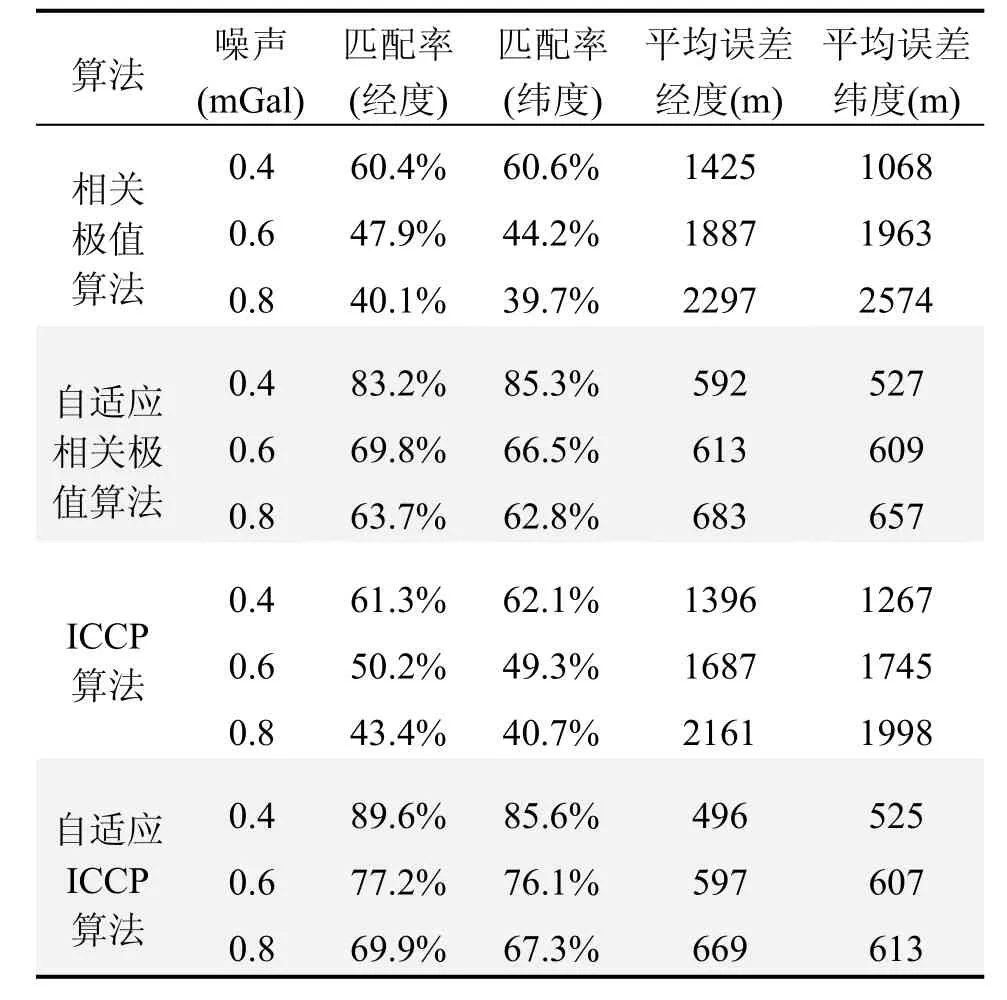
表1 匹配算法的匹配结果对比(阈值Γ =227 m)Tab.1 Matching results comparison of the algorithms (threshold value Γ =227 m)

4 结 论

本文从重力辅助导航误差差生的定性定量分析入手，通过定义不同的特征区间进行特征区域相似性划分,给出了重力辅助匹配算法引入整个惯性导航系统的自适应确定原理、方法及具体运算公式，最终实现了传统重力辅助匹配算法的自适应化，克服了盲操作问题。理论分析和计算机仿真试验都证明该方法能够有效地提高重力辅助导航算法的匹配率和精度。

References)

[1] Wang H B, Wang Y, Fang J. Simulation research on a minimum root-mean-square error rotation-fitting algorithm for gravity matching navigation[J]. Science China Earth Sciences, 2012, 55(1): 90-97.

[2] 李姗姗，吴晓平，马彪. 水下重力异常相关极值匹配算法[J]. 测绘学报，2011，40(4)：464-470.

Li S S, Wu X P, Ma B. Correlative extremum matching algorithm using underwater gravity anomalies[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 464- 470.

[3] Chen Y, Xiu C B, Luo J. The simulation of ICCP algorithm in the gravity aided navigation[J]. Second International Conference on Intelligent Networks and Intelligent Systems, 2009: 25, 62-65.

[4] Yuan G N, Zhang H W, Yuan K F. A combinational underwater aided navigation algorithm based on TERCOM/ICCP and Kalman filter[J]. IEEE Journal of Sciences and Optimization, 2011, 23(1): 952-955.

[5] Senobari M S. New results in airborne vector gravimetry using strapdown INS/GNSS[J]. J Geoid, 2010, 84: 277-291.

[6] 郭秋英，徐遵义. 水下重力辅助导航中重力测量误差改正研究[J]. 地球物理学进展，2012，27(3)：1274-1279.

Guo Q Y, Xu Z Y. Study on error correction of gravity surveying in underwater gravity aided navigation system [J]. Progress In Geophysics, 2012, 27(3): 1274-1279.

[7] 李胜全，欧阳永忠，常国宾. 惯性导航系统重力扰动矢量补偿技术[J]. 中国惯性技术学报，2012，20(4): 410-414.

LI Sheng-quan, OUYANG Yong-zhong, CHANG Guo-bin. Compensation technology of gravity disturbance vector in inertial navigation system[J]. Journal of Chinese Inertial Techno- logy, 2012, 20(4): 410-414.

[8] Dransfield M, ZENG Y. Airborne gravity gradiometry: Terrain corrections and elevation error[J]. Geophysics, 2009, 74(5): 137-142.

[9] 骆迪，刘展，李曼，张旺. 重力校正中存在的若干问题[J]. 地球物理学进展，2013，28(1)：111-121.

LUO D, LIU Z, ZHANG W. Several issues in gravity correction[J]. Chinese Journal of Scientific Instrument, 2013, 28(1): 111-121.

[10] 童余德，边少锋，蒋东方.基于高斯样条函数的局部重力异常场解析重构. [J].测绘学报, 2012，41(5)：756-760.

TONG Yu-de, BIAO Shao-feng, JIANG Dong-fang. The recon- struction of local gravity anomaly field based on spline function[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5)：756-760.

[11] Mcphail S. Autosub6000: A deep diving long range AUV [J]. Journal of Bionic Engineering, 2009, 6: 55-62.

[12] Markiel J N, Grejner-Brzezinska D, Toth C, et al. Underwater mapping and navigation: Applications of 3D feature extraction algorithms to 3D sonar datasets[C] //Institute of Navigation - International Technical Meeting. 2010. vol.1: 618-628.

[13] Siouris G M. Gravity modeling in aerospace applications [J]. Aerospace Science and Technology, 2009, 13(6): 301-315.

Adaptive intervention matching algorithm based on gravity aided navigation error analysis

WEN Chao-bin1,2, WANG Yue-gang1, GUO Zhi-bin1, TIAN Qi1, ZUO Zhao-yang1, TENG Hong-lei1
(1. 304 Unit, The Second Artillery Engineering University, Xi’an 710025, China; 2. Unit 96124 of the Chinese People’s Liberation Army, Tonghua 134000, China)

Traditional gravity aided matching algorithms are difficult to apply since its matching precision and matching proportion are too low due to being influenced by measurement and no-measurement errors. To solve this problem, an adaptive intervention matching algorithm is proposed by theoretically analyzing its error source. By adjusting the features space of equal point and the relationship between threshold value and closest range, the algorithm can adaptively correct INS position parameters, which greatly improves the searching efficiency, matching probability and real-time calculation speed. Simulation experiment results show that, after processing by this adaptation procedure, the optimal matching probability is increased to 89.6%, the positioning accuracy error is within 500～700 m, and the gravity map resolution (1') is reduced by 75%.

gravity aided navigation; error analysis; matching algorithm; adaptive

联 系 人：王跃钢（1958—），男，教授，博士生导师。E-mail：weijing123@126.com

1005-6734(2014)04-0514-05

10.13695/j.cnki.12-1222/o3.2014.04.017

U666.1

A

2014-03-28；

2014-07-15

国防预研（103030203）

文超斌（1986—），男，博士研究生，从事导航、制导与控制研究。E-mail：weijing123@126.com