球面单形平方根无迹粒子滤波在拖曳合成孔径声纳组合导航中的应用

李厚全，刘莫尘，伍志海，李伟刚

（1. 海军潜艇学院，青岛 266044；2. 海军航空工程学院，烟台 264000；3. 山东农业大学，泰安 271018）

球面单形平方根无迹粒子滤波在拖曳合成孔径声纳组合导航中的应用

李厚全1，2，刘莫尘3，伍志海1，李伟刚1

（1. 海军潜艇学院，青岛 266044；2. 海军航空工程学院，烟台 264000；3. 山东农业大学，泰安 271018）

惯性导航设备修正回波数据作为合成孔径声纳（SAS）运动补偿的一种重要方法，其中的关键技术是研究和利用高精度的滤波算法以及组合导航系统为运动补偿提供导航数据信息。在标准粒子滤波算法的基础上进行改进，提出了一种球面单形平方根无迹粒子滤波算法（SS-SRUPF），并将之应用于SINS、多普勒计程仪（DVL）组成的水下组合导航系统，输出的导航数据再传输给SAS成像系统。仿真结果表明，SS-SRUPF算法可将一个合成孔径时间内的组合导航位置均方误差精度提高到 0.013 m，小于SAS距离向分辨力0.019 m，满足SAS运动补偿的要求。

合成孔径声纳；组合导航；粒子滤波；运动补偿

SAS的运动补偿通常可采用基于惯性测量系统的运动补偿和基于回波数据的运动补偿两种方法。基于惯性测量系统的运动补偿的关键技术之一是利用高精度水下组合导航方法对安装在拖体上的 SAS进行实时的姿态测量和运动误差估计。导航系统测量并给出SAS姿态和位置，计算给出平均理想直线航迹[1]，以确保运动补偿相对此理想航迹进行，根据测量数据计算出阵元相位中心的实际位置，然后补偿掉实际位置相对理想直线航迹的偏差[2]。水下拖曳式合成孔径通常包含三个子系统：拖曳子系统、信号处理子系统、显控子系统。其中，拖曳子系统包括绞车、沉鱼和拖体。拖体内包含声纳子系统、导航子系统和数据采集与处理子系统，拖体内的配置见图1。SAS导航系统配置包括SINS、声学多普勒计程仪和深度计。正是基于上述SAS导航子系统的导航方案，研究了由SINS、声学多普勒计程仪以及高精度石英深度计等设备组成的的姿态和位移测量组合导航系统。

当导航姿态误差角较大时，组合导航系统方程采用非线性方程更为精确，因此采用四元数法建立大姿态误差角下SINS/DVL组合导航系统方程。系统方程的滤波算法即成为一高维非线性系统滤波问题。

粒子滤波算法（PF）是近些年备受关注的一种处理非线性问题的贝叶斯状态估计算法，在导航系统中已有诸多报道[3-7]。它通过带有归一化权重的粒子集来近似表示后验概率密度[8-9]，采用扩展卡尔曼滤波（EKF）、无迹卡尔曼滤波（UKF）等算法结合最新观测值产生建议密度分布[10-11]的方法解决粒子退化问题都存在弊端，如EKF只能精确到一阶近似，UKF无迹粒子滤波（UPF）对高维滤波问题计算量偏大。

从降低计算量、提高系统估计精度的角度出发，将UPF算法进行改进，提出了一种球面单形平方根无迹粒子滤波算法（SS-SRUPF），并应用于大姿态误差角情况下基于四元数法的SINS/DVL组合导航系统，仿真结果表明，提出的SS-SRUPF算法相比常规UPF算法大大降低了计算量，提高了系统估计精度。

1 SAS运动估计的导航系统方程

SAS所用拖体内的配置[12-13]如图1所示，拖体长约4.4 m，线列阵长约2 m。导航方案采用SINS、DVL和深度计组合。对于SAS影响最大的主要是水平面内信息（侧摆和偏航角）的影响，横滚角对InSAS（干涉合成孔径）影响较大。因此，水平面内的导航信息对SAS可采用组合导航模式，深度方向采用深度计测量。

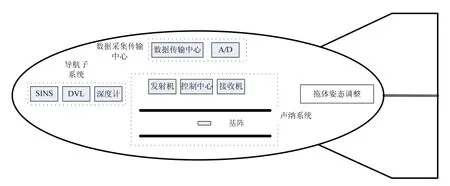
图1 导航系统在SAS拖体系统中的配置Fig.1 Navigation system in the towfish of SAS

针对上述设计的SAS导航方案，组合导航系统采用四元数法建立SINS/DVL系统误差方程[14]，系统状态方程和观测方程建立如下：

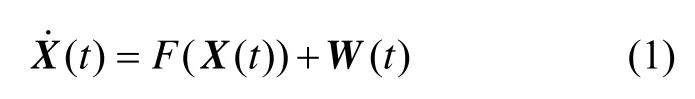
上述系统状态方程中，状态变量为：

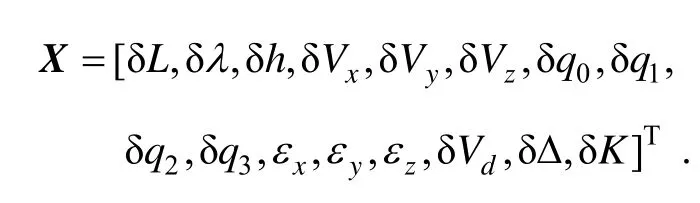
式中，δL、δλ、δh分别为纬度、经度、高度误差；δVx、δVy、δVz分别为相应的速度误差；δ q0、δ q1、δ q2、δ q3为计算四元数与真实四元数的差；εx、εy、εz为SINS的系统随机误差；δVd是DVL采用底跟踪模式时的观测误差，主要是指速度偏移误差，δK为刻度系数误差，δΔ偏流角误差。

将SINS计算出的系统速度误差与DVL测速误差之差作为系统的量测值，得系统的量测方程为：

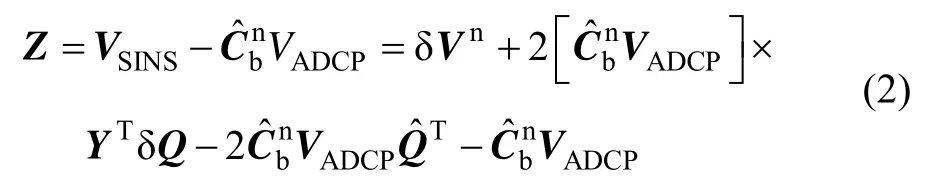
2 SS-SRUPF算法

一般离散非线性系统可表述如下：

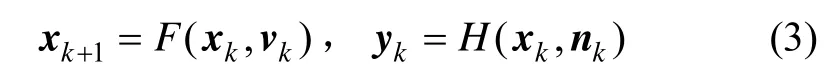
式中， xk为状态向量；vk为系统噪声，其方差为 Pv；nk为量测噪声，其方差为 Pn。

对于上述系统，提出了球面单形平方根无迹粒子滤波算法（SS-SRUPF），该算法选用SS-SRUKF作为粒子滤波算法的建议密度，其参加计算的sigma点约为 UPF算法中 UKF所用 sigma点数量的一半，且SR-UKF本身也比UKF计算效率也有较大的提升。

SS-SRUPF详细算法如下：

①初始化： k=0

从先验分布 p(x0)中采样粒子集，i =1,…, Ns。并设为如下初始条件：

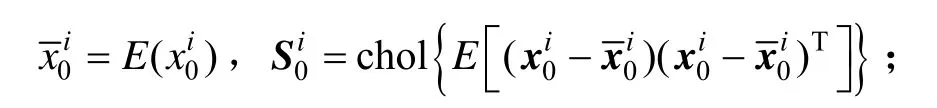
② 对于 k-1测量时刻计算 sigma点，选取权值W0，且满足 0 ≤ W0≤ 1。确定权值序列，满足：Wl=(1 - W0)(n +1)， l = 1,… ,n+1。

初始化sigma点向量序列：

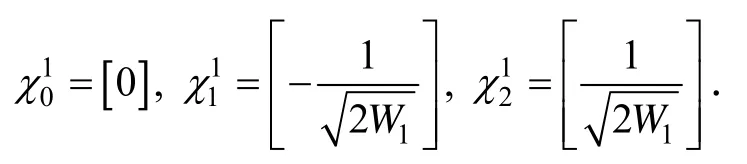
迭代计算sigma点向量，扩展维数 j =2,… ,n：

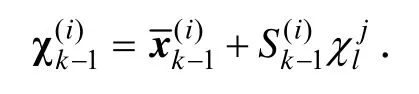
式中，

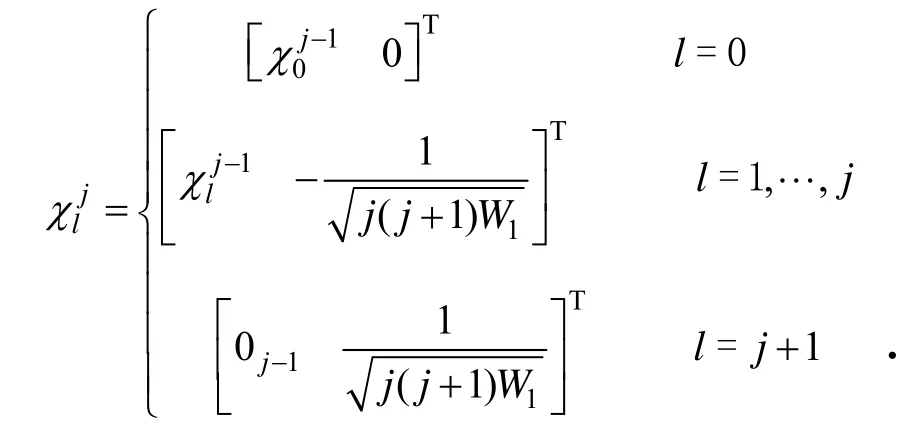
SS-SRUKF时间更新方程：

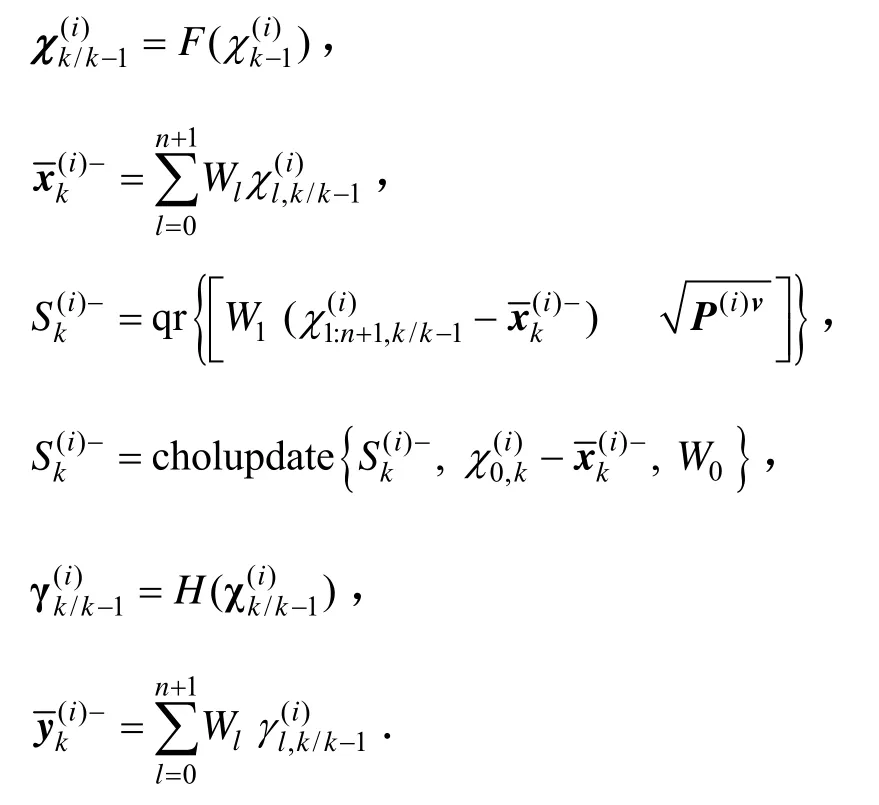
SS-SRUKF量测更新方程如下：

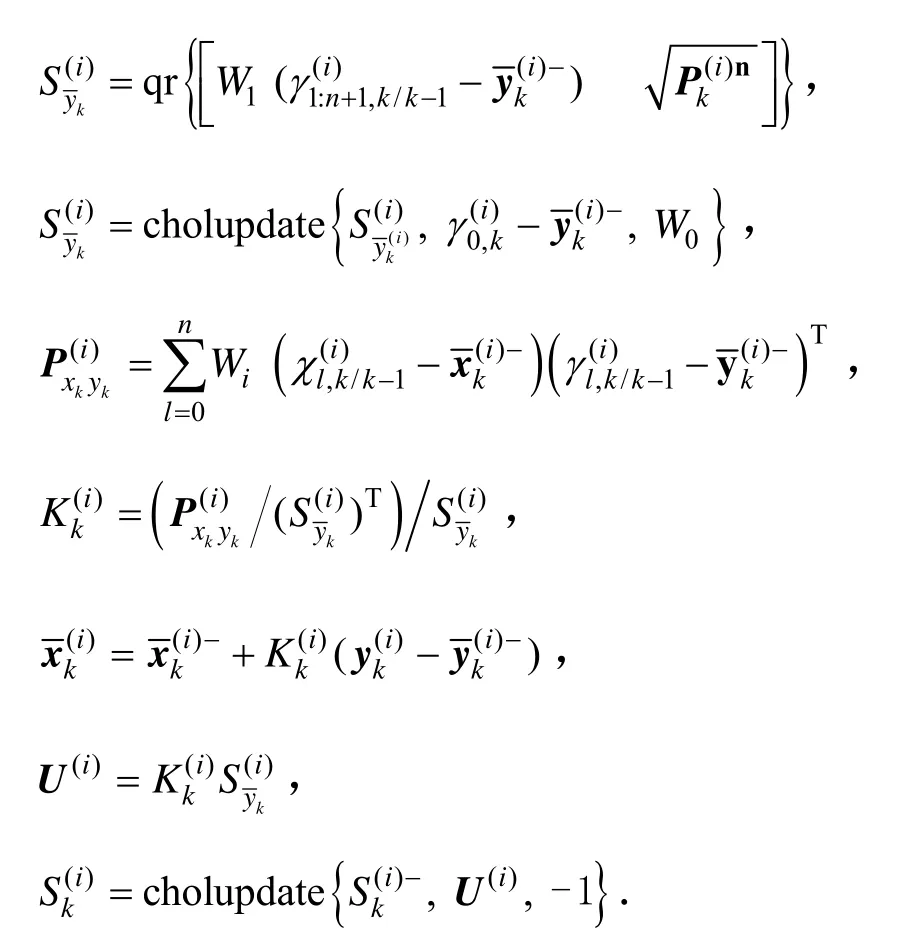
式中，Pv为过程噪声向量， Pn为测量噪声向量。

③ 以SS-SRUKF得到的状态估计和方差为建议密度分布，从中采样 Ns个粒子：

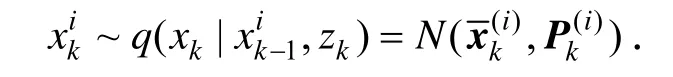
④ 重采样：

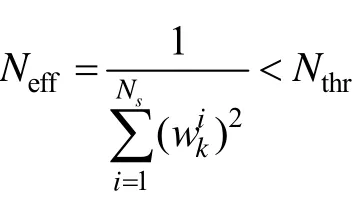
⑤ 状态输出和方差：

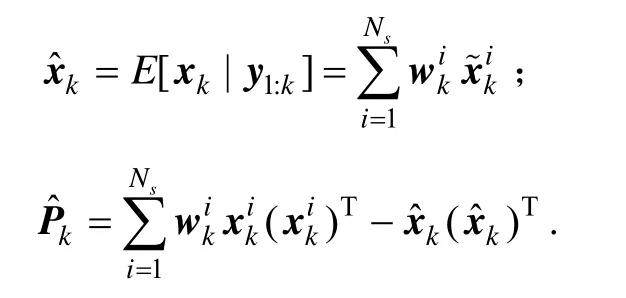
上述过程为SS-SRUPF的完整算法，采样得到的每个粒子传递均值和方差信息，采用的算法为 n+ 2球面单形sigma点的UKF算法。为验证SS-SRUPF算法的优越性，第3部分进行了仿真算法验证。

3 SS-SRUPF仿真与分析

SAS由舰船牵引在水下运动，其运动规律用速度方程和姿态角表达如下[7]：

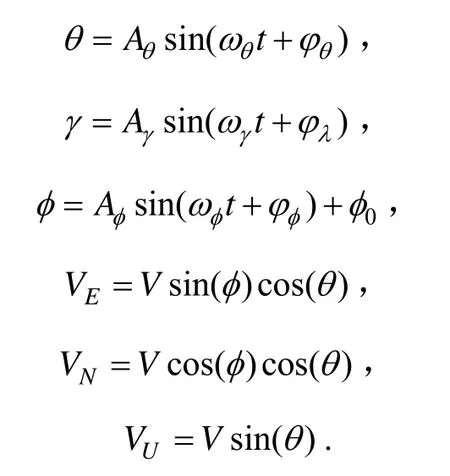
其中，VE、VN、VU分别为东北天坐标系下的速度分量；V为SAS所在载体轴向速度设定为3 m/s；θ、γ、φ为SAS载体纵倾角、横滚角和方位角；ωθ、ωγ、ωφ为姿态角角频率，其相应周期分别设为12 s、6 s、10 s；Aθ、Aγ、Aφ为姿态角摇摆幅度，分别设为6°、4°、3°；φθ、φλ、φφ分别为姿态角初始相位，均设为45°，φ0为SAS初始航向设为45°。SINS陀螺常值漂移0.1 (°)/h，加速度计常值漂移± 500 μg；DVL测速误差垂直测速误差0.6%，水平速度误差0.2%。初始经度120°，纬度60°。

为验证所提出算法的性能，依据SAS水下试验方案，在同一仿真条件下，分别采用SS-SRUPF以及PF、UPF三种算法对SINS/DVL导航系统方程进行滤波处理。在CPU为AMD 4核 2.0 GHz，内存为2.0GB的PC机上，分别对三种算法进行50次蒙特卡洛仿真，选取粒子数目1200。

仿真结果如图2、图3、图4以及表1所示。由图中结果可以看出，SS-SRUPF算法滤波精度高于标准粒子滤波算法（PF）和UPF算法，由此看见粒子滤波算法中建议密度的合理选择对提升粒子滤波的性能有着至关重要的作用，仿真结果与前面的理论分析完好的吻合。SS-SRUPF与UPF相比，滤波精度提高，且计算效率较UPF算法提高一倍。

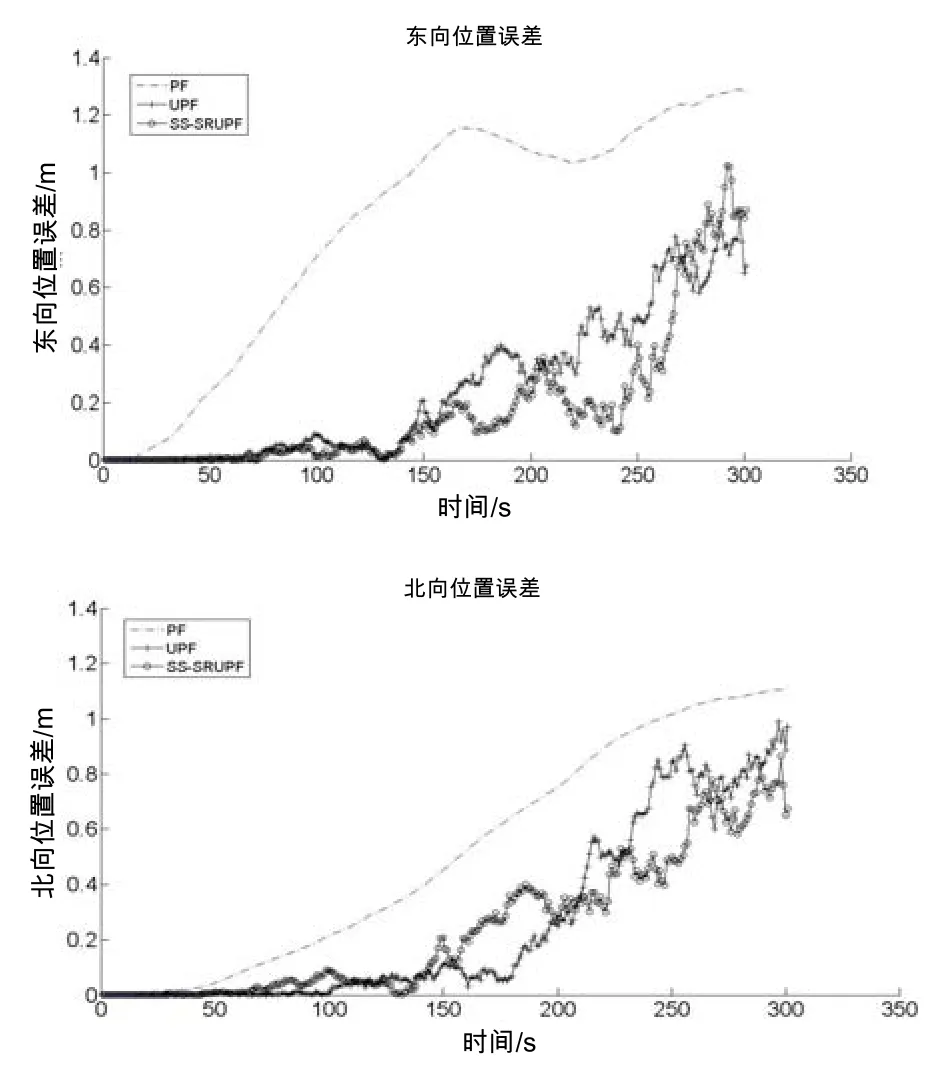
图2 位置误差Fig.2 Position error

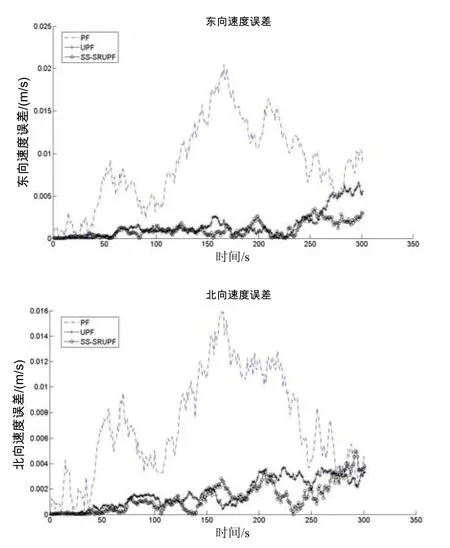
图3 速度误差Fig.3 Velocity error

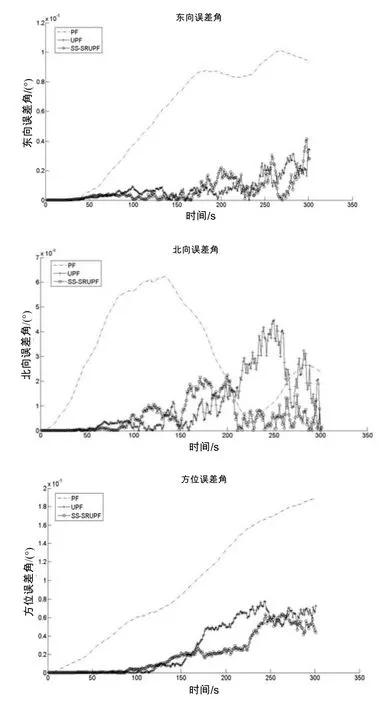
图4 方向误差角Fig.4 Attitude angle error

表1 PF、UPF以及SS-SRUPF估计精度Tab.1 Precision comparing among PF, UPF and SS-SRUPF algorithms

由表1水平面内位置估计精度可以计算得到PF、 UPF以及SS-SRUPF的航路估计（航速3 m/s）误差精度分别达到航程的0.19%、0.14%、0.13%。此外，偏流角的误差估计精度，三种算法都在0.1°以内。

对于系统参数如表2所示的SAS成像系统，经计算其距离向分辨力为：

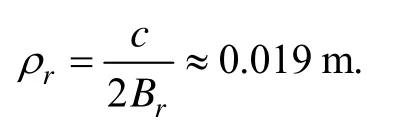
其中，c表示水声传播速度， Br为信号带宽。

一个合成孔径时间为：

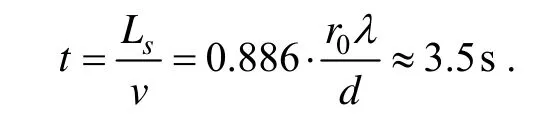
其中， r0为成像距离，λ为波长，d为声纳基阵宽度。

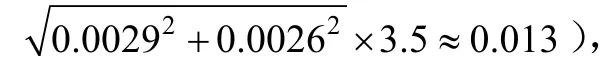
表2 系统仿真参数Tab.2 System and simulation parameters

4 结 论

针对非线性导航系统误差方程的滤波为一高维非线性滤波问题，改进提出的采用球面单形平方根无迹粒子滤波算法，相比UPF算法和PF算法能够有效提高组合导航系统的估计精度，计算效率也比UPF大大提高，其滤波精度完全满足合成孔径声纳运动补偿对导航数据的要求，为合成孔径声纳运动补偿提供了数据和技术支持。

（References）：

[1] 张远彪，朱三文. 多子阵合成孔径声纳空变运动补偿[J].计算机应用，2014，34(S1)：352-355.

ZHANG Yuan-biao, ZHU San-wen. Space-variant motion compensation for multi-element synthetic aperture sonar[J]. Journal of Computer Applications, 2014, 34(S1): 352-355.

[2] Hayes M P, Gough P T. Synthetic aperture sonar: A review of current status[J]. IEEE J. Oceanic Eng., 2009, 34(3): 207-224.

[3] Ali J, Mirza M R U B. Performance comparison among some nonlinear filters for a low cost SINS/GPS integrated solution[J]. Nonlinear Dynamics, 2010, 61(3): 491-502.

[4] 熊剑，郭杭，熊智，等. GPS/INS 组合导航系统中的高斯粒子滤波混和算法[J]. 中国惯性技术学报，2012，20(2)：596-600.

XIONG Jian, GUO Hang, XIONG Zhi, et al. Gaussian particle filtering hybrid algorithm for GPS/INS integrated navigation system[J]. Journal of Chinese Inertial Technology, 2012, 20(2): 596-600.

[5] Scharcanski J, Oliveira A B, Cavalcanti P G, Yari Y. A particle filtering approach for vehicular tracking adaptive to occlusions[J]. IEEE Transactions on Vehicular Technology, 2011, 60(2): 381-389.

[6] Jacques G, Tashfeen K, Umar I, et al. Enhanced MEMSIMU/odometer/GPS integration using mixture particle filter[J]. GPS Solutions, 2011, 15(3): 239-252.

[7] 吴鑫辉，黄高明，高俊. 未知噪声统计下多模型概率假设密度粒子滤波算法[J]. 控制与决策，2014，29(2)：1-6.

WU Xin-hui, HUANG Gao-ming, GAO Jun. Multiplemodel probability hypothesis density filter for multi-target tracking without the statistics of noise parameters[J]. Control and Decision, 2014, 29(2): 1-6.

[8] Stordal A S, Karlsen H A, Nævdal G, et AL. Bridging the ensemble Kalman filter and particle filters: the adaptive Gaussian mixture filter[J]. Computational Geosciences, 2011, 15(2): 293-305.

[9] Kim J, Vaddi S S, Menon P K, Ohlmeyer E J. Comparison between nonlinear filtering techniques for spiraling ballistic missile state estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 313- 328.

[10] Stordal A S, Karlsen H A, Nævdal G, et al. Bridging the ensemble Kalman filter and particle filters: the adaptive Gaussian mixture filter[J]. Computational Geosciences, 2011, 15(2): 293-305.

[11] Julier S J. The spherical simplex unscented transformation [C]//Proc Amer Control Conf, 2003, vol.3: 2430-2430.

[12] 张森，唐劲松，陈鸣，等. 干涉合成孔径声纳海试样机研制与试验[J]. 声学技术，2012，31(2): 167-173.

ZHANG Sen, TANG Jing-song, CHEN Ming, et al. Development and sea trial of interferometric synthetic aperture sonar[J]. Technical Acoustics, 2012, 31(2): 167-173.

[13] Zhang Sen, Tang Jingsong. Image autocoregistration and interferogram estimation using extended COMET-EXIP method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(12): 4204-4218.

[14] 李厚全，李 恒，唐劲松，等. Unscented粒子滤波算法在合成孔径声纳组合导航中的应用研究[J]. 海军工程大学学报，2010，22(3)：26-31.

LI Hou-quan, LI Heng, TANG Jin-song et al. The research of Unscented particle filter used in the navigation of SAS[J]. Journal of Naval University of Engineering, 2010, 22(3): 26-31.

Spherical simplex square-root unscented particle filter used in integrated navigation system of synthetic aperture sonar

LI Hou-quan1,2, LIU Mo-chen3, WU Zhi-hai1, LI Wei-gang1
(1. Navy Submarine Academy, Qingdao 266044, China; 2. Naval Aeronautical Engineering Institute, Yantai 264000, China; 3. Shandong Agricultural University, Taian 271018, China)

In motion compensation of synthetic aperture sonar(SAS), one of important methods is using inertial navigation system to correct the echo data. In this paper, a high-precision filter algorithm and integrated navigation system were studied and utilized for providing navigation data to realize the motion compensation. A new algorithm, i.e. spherical simplex square root unscented particle filter(SS-SRUPF), is proposed and applied into the integrated SINS/DVL navigation system. The navigation data from the integrated system is then transferred to the SAS imaging system. Simulation results indicate that the integrated navigation precision in a synthetic aperture time is increased to 0.013 m(RMS) which is smaller than the SAS range differentiability of 0.019 m, and the computation efficiency is more than twice the UPF’s, meeting the motion compensation requirement of SAS.

synthetic aperture sonar; inertial navigation; particle filter; motion compensation

李厚全（1981—），男，博士，讲师，从事组合导航、水声信号处理研究。E-mail： lhqqtxy@163.com

1005-6734(2014)04-0531-05

10.13695/j.cnki.12-1222/o3.2014.04.020

U675.7

A

2014-04-25；

2014-07-24

国家高技术研究发展计划（863计划）（2007AA091101）；中国博士后基金资助（2014M552658）