基于自适应卡尔曼滤波的简化地磁定轨
2014-10-21吴云华康国华
郁 丰,华 冰,吴云华,康国华
(南京航空航天大学 航天学院,南京 210016)
基于自适应卡尔曼滤波的简化地磁定轨
郁 丰,华 冰,吴云华,康国华
(南京航空航天大学 航天学院,南京 210016)
地磁定轨对追求低成本、高功能密度比的微小卫星具有较重要的价值,但是目前地磁定轨尚存在计算量大、易受各类误差影响导致精度过低等不足。在分析轨道动力学方程误差量级的基础上,建立了简化的状态转移矩阵,根据地磁模型分析了地磁强度随着阶次变高,梯度显著变小的特点,提出了高阶截断的简化地磁测量方程;将复杂的磁强计测量误差近似建模成随机游走形式,用多项式对磁强计误差估计值进行实时拟合去噪,并辨识出磁强计误差的变化特征作为自适应卡尔曼滤波器的调节依据,提高了弱可观测地磁定轨的性能。数学仿真证明了简化地磁定轨模型的有效性,自适应滤波器能够更精确地实现定轨计算,定位精度约为6 km,测速精度约为4 m/s。
自主导航;地磁定轨;国际地磁参考场;自适应卡尔曼滤波器
随着航天技术的飞速发展,微小卫星自主定轨已经成为卫星轨道测量领域的发展方向。地磁导航是一种特别适合近地微小卫星的中低精度定轨方法[1]。由于近地轨道上有丰富的地磁场资源,并且地磁场可以采用高斯球谐函数来描述,磁场的强度与方向能表示为卫星位置的函数[2],所以可用磁测的方法对卫星进行自主定轨。目前微小卫星普遍安装三轴磁强计作为星上的定姿敏感器,如果能够将磁强计复用作定轨传感器,能进一步满足微小卫星轻质量、小功耗、高可靠性和低成本的要求。
自从美国Cornell大学的学者首先提出测量地球磁场来确定卫星轨道的概念以来,已经有较多文献讨论了地磁定轨技术。一般采用地磁场的模或者磁场矢量,并结合卡尔曼滤波技术实现了定轨计算,文献[3]建立了地磁定轨的基本方法。为进一步解决地磁定轨精度低的不足,文献[4-6]提出了地磁场信息结合太阳或者星光矢量来提高定位精度的方法,仿真研究表明效果明显;另一方面,地磁定轨精度低导致了 EKF在一阶线性截断时误差较大,文献[7-10]采用UKF/PF算法改善了定轨计算的性能。上述方法较少讨论磁强计测量误差等因素导致的定轨性能下降的问题,文献[11]探讨了在标定磁强计零偏与比例因子误差条件下的定轨方法。
本文分析了地磁模型高阶项梯度显著减小的特点,提出了地磁模型截断高阶项保留低阶项来建立测量方程的方法,同时考虑到地磁定轨精度相对较低,并且卡尔曼滤波器能持续修正轨道参数,所以忽略了中心引力 1‰及以下的项,建立了简化地磁定轨的数学模型,一定程度上降低了计算复杂度;另一方面,地磁定轨是一个弱可观测性系统,磁强计测量误差会导致较大定轨误差,所以本文将误差成分复杂的磁场测量误差作为待估计项,并近似建模成随机游走形式,然后在轨统计磁场测量误差的变化率作为自适应滤波器的调节依据,提高了在时变磁场测量误差条件下的地磁定轨精度。
1 简化地磁定轨模型
1.1 地磁定轨的状态方程
采用卫星轨道动力学方程作为地磁定轨的状态方程,本文在地球固联坐标系中描述卫星轨道动力学方程,从而简化后续测量方程的建模,若用户需要地心惯性系中的定轨参数,可通过地固系与惯性系之间的坐标转换得到。由于地磁定轨精度相对较低,所以在诸多的摄动力中仅考虑 J2摄动项,则轨道预报模型如下:

式中,μ为地球引力常数, J2为二阶的带谐项系数,Re为地球的参考半径,ω为地球的自转角速度,f为其余摄动力。
采用扩展卡尔曼滤波器实现定轨计算需要对状态方程线性化得到线性干扰方程,由于基于卡尔曼滤波器的定轨过程是采用观测值不断修正的过程,待估状态量的改正值已经较小,同时考虑到两次修正间隔的定轨弧段很短,并且地磁定轨的精度相对较低,所以对状态转移矩阵进行简化。根据数量级估算,忽略近地轨道上不大于中心引力 1‰的项,在计算状态转移矩阵时的轨道动力学模型可以简化成:
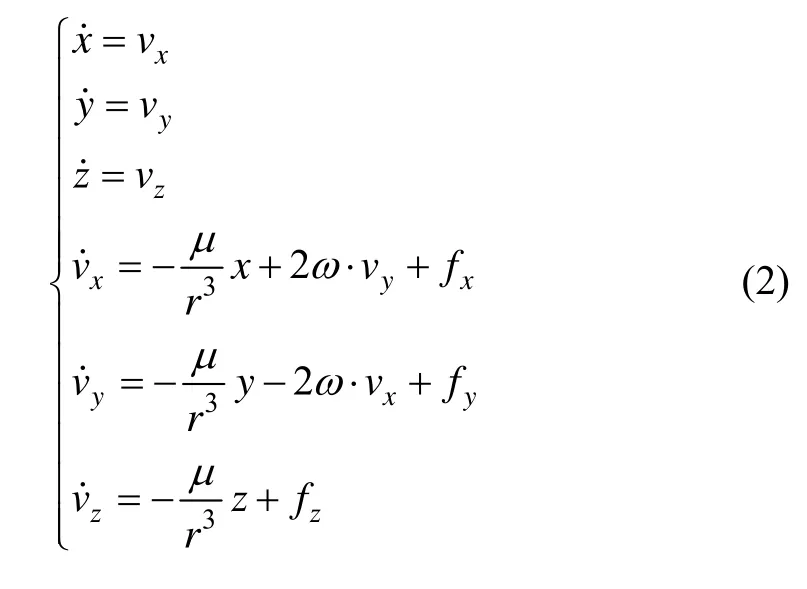
经过泰勒级数展开并保留一阶项,并对该方程离散化,得到离散型线性干扰方程式:
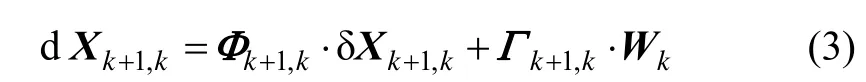
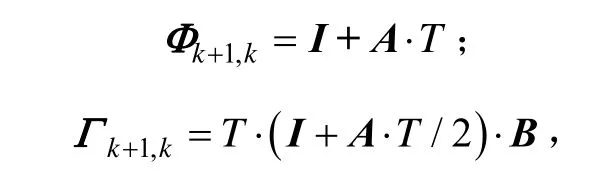
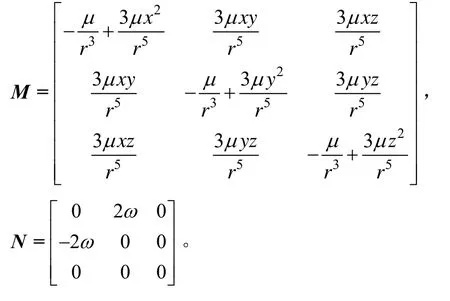
1.2 地磁定轨的测量方程
地磁场常采用国际参考地球磁场模型(IGRF)描述,磁位势的函数为:
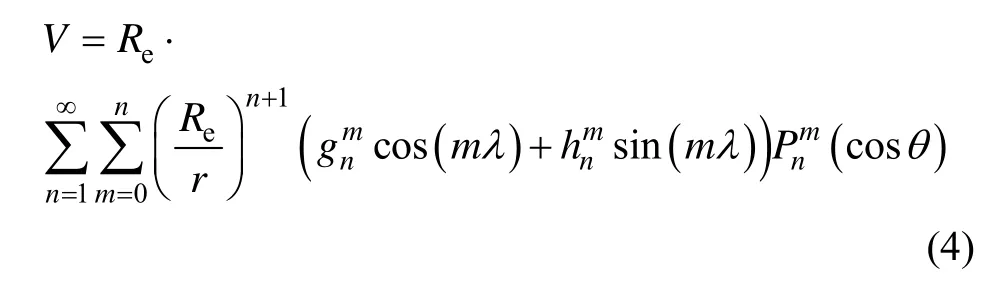
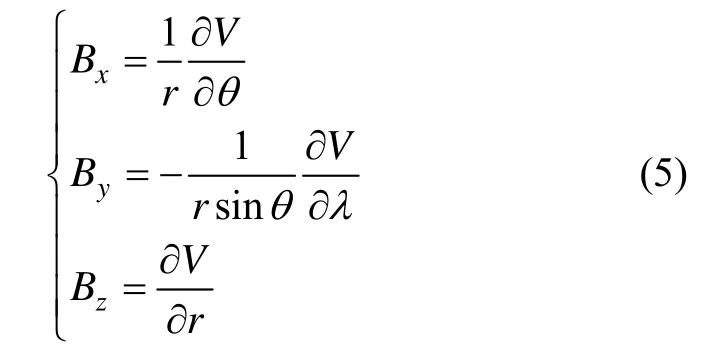
由于微小卫星的姿态测量精度有限,所以采用磁场强度的模作为观测值,这样卫星定轨计算不依赖卫星的姿态,更方便星上使用,则测量方程有:
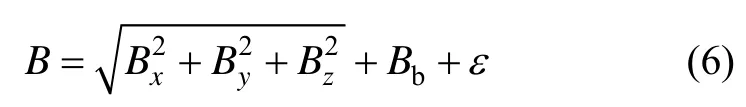
式中,ε为测量噪声,磁强计该部分误差并不大,例如某型卫星用磁强计噪声为数nT, Bb为磁强计测量的偏置误差,该误差包含磁强计三轴合成的标定因子误差、磁强计零偏、软磁周期磁化导致的测量误差等,由于这些误差项很难在地面实验室条件下精确的测量,或者也并不是一成不变的,所以很难精确建模,但是这些误差会受在轨地磁场变化或者磁强计的工作时间而缓慢改变,从而影响地磁定轨的精度。所以将 Bb扩充到状态方程中,并将其建模成随机游动形式来近似:

线性化得到相应的干扰方程为:

同样对测量方程线性化,得到测量方程的线性干扰方程,则有:
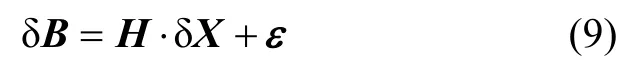
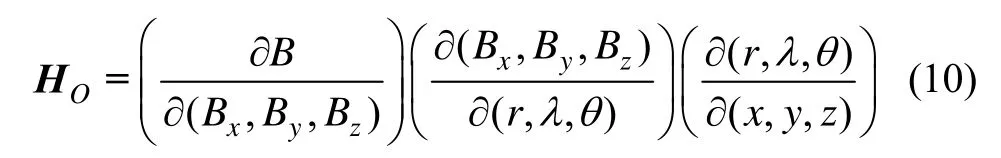
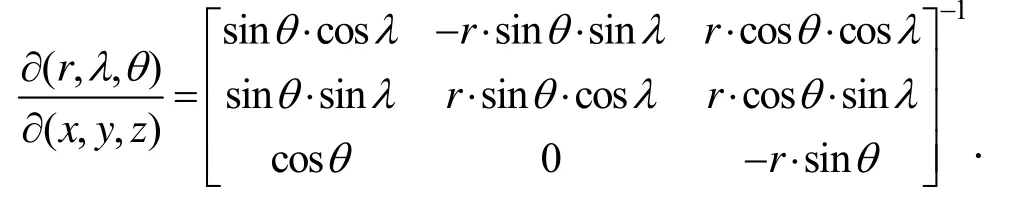
对式(10)中的第 2个偏微分矩阵进行研究分析表明,随着磁场模型的阶次越高,不但对应的磁场强度越小,而且其位置梯度变化也越小,所以磁场模型的高阶偏微分项对轨道精密修正的作用也越小;另一方面,利用磁场模型低阶项估计出大部分轨道误差后,剩余轨道误差导致的磁场模型高阶项对应的磁场强度差异是可以近似忽略的。同时,磁场模型阶次越高,该阶的计算量也越大,所以为节约星上运算量可以考虑该偏微分矩阵的计算仅考虑磁场模型低阶项,则有:
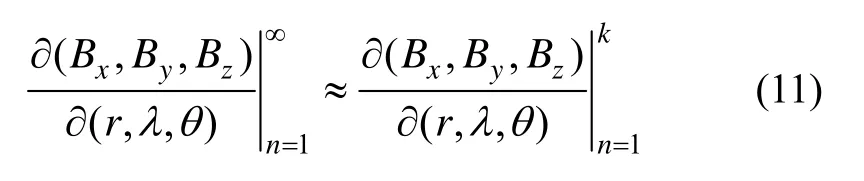
式中,k为低阶截断阶次。
2 自适应卡尔曼滤波器的设计
根据第1节中的简化地磁定轨模型,采用扩展卡尔曼滤波器即可实现轨道估计。但是地磁场定轨是一个弱可观测系统,所以当磁强计存在测量误差并且不能准确在轨估计时,会导致定轨精度的下降。根据式(7)可知,磁强计误差建模成随机游走的形式是一定精度的近似,并且很难进行高精度的建模,拟对 Bb的估计值进行实时检测与判断,当 Bb偏离常值时适当放大相应的动态噪声,从而更置信于测量值,得到对 Bb更准确的估计,当 Bb更表现出常值特征时适当减小相应的动态噪声,从而更置信于状态预报值,通过这样的自适应方法的处理,能进一步改善地磁定轨的精度。为消除 Bb的估计误差对 Bb数据特征检测与判别的影响,首先利用一系列进行多项式拟合,
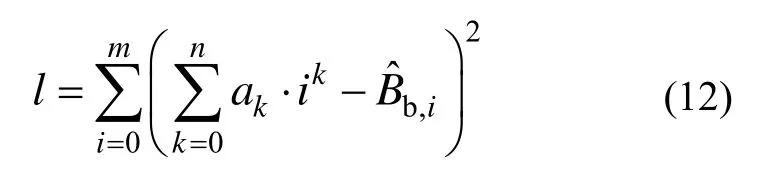
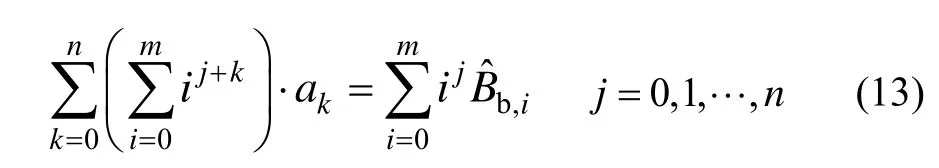
利用求得的拟合系数计算得到当前的 Bb的拟合值,利用一系列的平滑后的后,前后做差判断Bb的数据变化趋势,
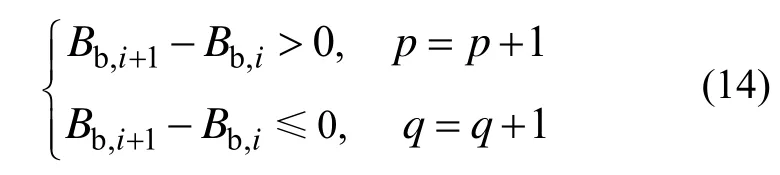
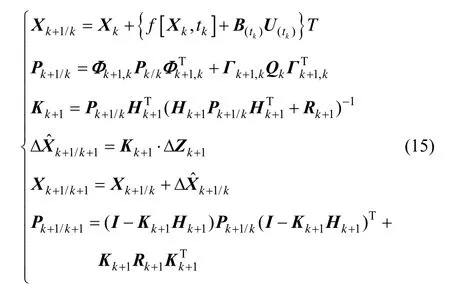
3 仿真与验证
首先开展地磁导航测量方程对应的线性干扰方程采用低阶地磁模型的可行性论证分析,设置两条相近轨道,并让其初始时刻在相同的位置,经过一段时间飞行后,两者位置差异约为14 km,如图1中的横坐标所示。图1中的1号曲线指的是地磁模型均取到4阶时,两地的地磁强度差异;图1中的2号曲线指的是地磁模型的5~10阶对应的两地磁场强度差异。由此可见,两地的位置差异导致的地磁强度差异主要体现在低阶项上,仿真表明随着阶次变高,磁场强度的梯度越小,所以求取测量线性干扰方程的观测矩阵时可以仅考虑地磁模型的低阶项,忽略掉计算更耗时、估计作用并不大的高阶项,经过卡尔曼滤波的序贯修正,即可估计出大部分定轨误差。不同阶数的地磁模型的位置梯度差异比较本文不再罗列。值得指出的是,地磁场高阶项本身并不小,选取2条轨道中的1条,并计算10阶与4阶的地磁场强度差,达到数百至上千(如图2所示),说明在测量方程线性化过程中计算地磁场强度的预报值 Bˆ时是不能忽略地磁模型高阶项的。
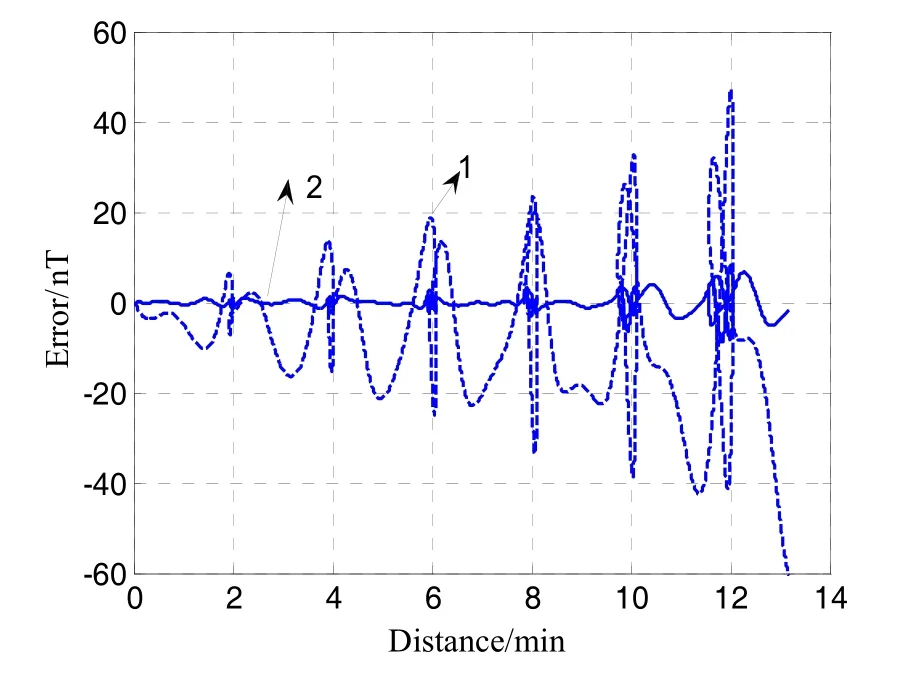
图1 地磁强度差与位置差的关系Fig.1 Geomagnetic intensity difference and position error
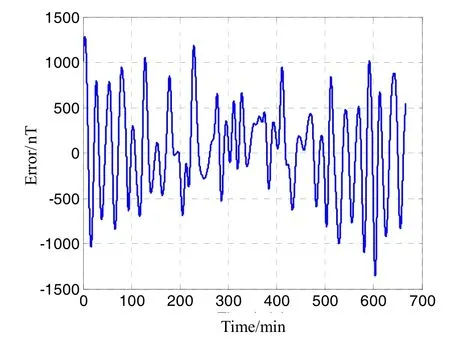
图2 某轨道的高阶地磁强度(5~10)Fig.2 Geomagnetic intensity of high order
然后利用仿真来研究简化模型与传统模型的轨道测量的性能分析,在标准轨道的模拟中,摄动力利用量级为[1E-7,0.5E-7,0.8E-7] N/kg,以轨道周期为周期的正弦函数来近似模拟,对应的滤波器Q值设置为1E-12,标准轨道初值为[6800 km 0 km 0 km 0 m/s 4000 m/s 6696 m/s],滤波器初值为[6 800 018 m -2119 m 2800 m 0.1 m/s 3999.8 m/s 6696.1 m/s],磁场真值采用IGRF10阶模型,磁强计测量误差包括300 nT的零偏,并认为其为随机游走的形式,其驱动噪声为0.01 nT/s,滤波器中对应的Q值设置为1 ,磁强计噪声为5 nT(1σ)。将传统方法与本文的简化方法仿真并比较,结果如图3、图4所示。
由图3、图4可知,两个方法在滤波器稳定后的精度是相当的,也证明了本文设计方法的正确性,在滤波收敛过程中简化方法比传统方法略差。综合来说本文可以减少5~10阶地磁模型的雅克比矩阵的计算,状态转移矩阵也更简洁,减少了星上计算量并最终实现了类似精度。
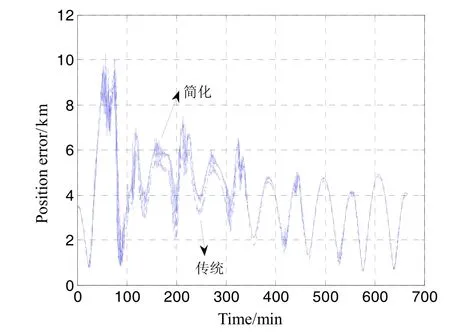
图3 简化与传统模型的定位误差Fig.3 Positioning errors of simplified & traditional model
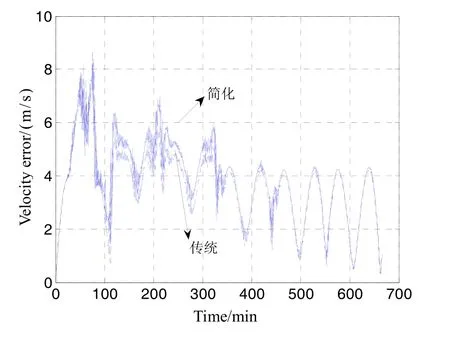
图4 简化与传统模型的测速误差Fig.4 Speed measuring errors of simplified & traditional model
最后分析论证自适应卡尔曼滤波在地磁定轨估计的作用,在前述仿真条件的基础上,进一步设定环境磁场30000 nT时导致的软磁磁化误差为30 nT,并假定软磁材料没有饱和,磁强计标定因子误差导致的测量误差如图5所示。由图5可见,仿真的磁强计误差在环境磁场30 000 nT以内则较小,25 000 nT以上时磁强计误差逐渐显著变大。设置3组滤波器,其中两组滤波器是常规的卡尔曼滤波器,其中Q值分别设置为1和8两个定值,对应图中的曲线分别为1和2,自适应滤波器的多项式拟合采用线性拟合,待拟合数据系列的长度设置为 100,用于判断数据变化趋势的数据序列长度为20,为简便和更好的说明效果,自适应滤波中的Q值动态地选择1和8两种值,判断阈值κ选为13,对应的滤波曲线为3。
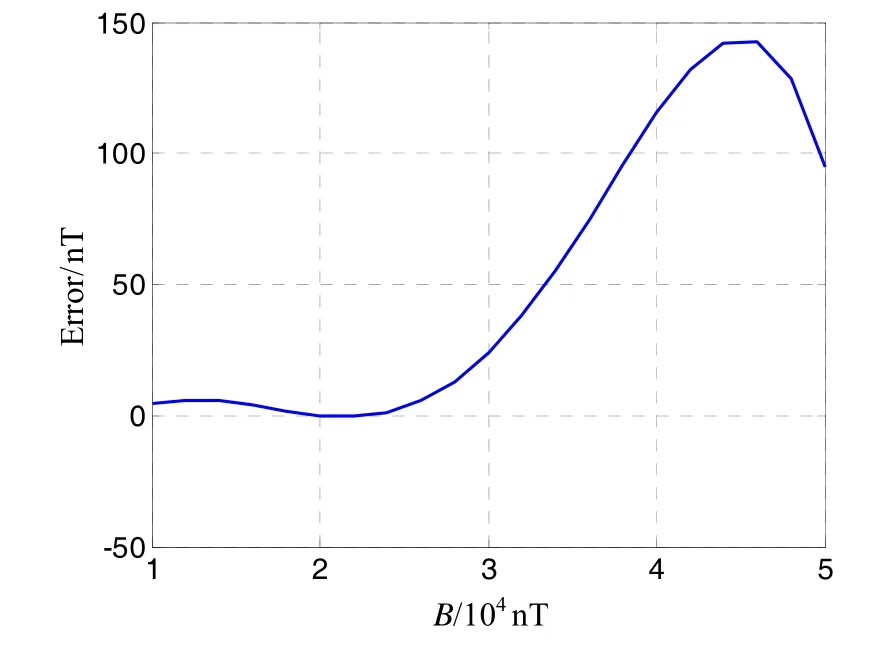
图5 模拟的磁强计标定因子误差Fig.5 Simulated error of magnetometer calibration factor

图6 自适应滤波与常规滤波器的定位精度Fig.6 Positioning errors of adaptive filtering and EKF
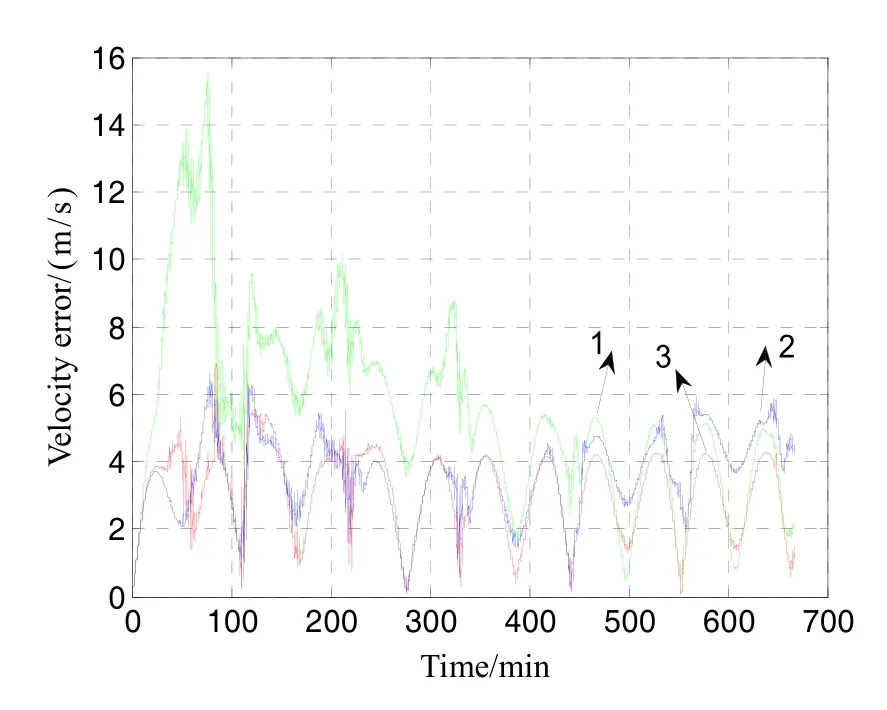
图7 自适应滤波与常规滤波器的测速精度Fig.7 Speed measuring errors of adaptive filtering and EKF
从图6、图7中可以看出,当Q较小时,滤波收敛过程中振荡较大,最大定位误差达18 km和16 m/s,而Q较大和自适应滤波器在收敛过程中没有出现大的振荡过程;当滤波器收敛稳定后,Q较大时对应的2号曲线的定位与测速误差最大,1号曲线次之。而自适应滤波器在整个定轨过程中,无论是收敛性能还是稳态精度都表现最佳。最终的定位精度约为6 km,测速精度约为4 m/s。
图 8表明,滤波器较好地跟踪了磁强计误差真值,采用线性拟合方式得到的平滑值也能较好地拟合估计曲线,当磁强计误差变化率较大时,通过自适应调节能够加速跟踪误差真值,而在磁强计误差变化率较小时,磁强计误差真值与平滑值基本重合,可见通过自适应策略较好地估计了磁强计误差,所以基于自适应滤波的地磁定轨方法具有更好的精度。

图8 磁强计误差的真值、估计值与平滑值Fig.8 True, estimated & smoothed value of magnetometer error
4 结 论
针对地磁定轨的计算量大,易受磁强计测量误差等因素的影响,本文在分析模型各项精度的基础上,推导了简化地磁定轨模型,然后采用多项式拟合实时去噪、辨识磁强计测量误差的变化特征,并采用自适应卡尔曼滤波实现了更高精度的地磁定轨。仿真证明了各项措施的有效性。
(References):
[1] Abdelrahman M, Park S Y. Simultaneous spacecraft attitude and orbit estimation using magnetic field vector measurements[J]. Aerospace Science and Technology, 2011, 15: 653-669.
[2] 刘元元,王仕成,张金生,等. 最新国际地磁参考模型IGRF11研究[J]. 地震学报,2013,35(1):125-134.
LIU Yuan-yuan, WANG Shi-cheng, ZHANG Jin-sheng, et al. Research on the eleventh generation IGRF[J]. Acta Seismologica Sinica, 2013, 35(1): 125-134.
[3] Psiaki M L, Huang Le-jin. Ground tests of magnetometerbased autonomous navigation for low-earth-orbiting spacecraft[J]. Journal of Guidance, Control and Dynamics, 1993, 16(1): 206-212.
[4] 谢祥华,张锐,张静. 基于磁强计与太阳敏感器的卫星自主定轨算法[J]. 宇航学报,2009,30(3):919-923.
XIE Xiang-hua, ZHANG Rui, ZHANG Jing. Satellite autonomous orbit determination based on magnetometers [J]. Journal of Astronautics, 2009, 30(3): 919-923.
[5] 刘睿,王常虹,李葆华. 利用地磁/星光观测角度的飞行器自主导航方法[J]. 红外与激光工程,2011,40(2):223-228.
LIU Rui, WANG Chang-hong, LI Bao-hua. Autonomous navigation method using the angle between geomagnetic and starlight vector[J]. Infrared and Laser Engineering, 2011, 40(2): 223-228
[6] Psiaki M L. Autonomous LEO orbit determination from magnetometer and sun sensor data[J]. Journal of Guidance, Control and Dynamics, 1999, 22(2): 296 -306.
[7] 王向磊,丁硕,苏牧丹. EKF/UKF在基于地磁场的卫星自主定轨中的应用比较[J]. 测绘科学技术学报,2011,28(1):50-53.
WANG Xiang-lei, DING Shuo, SU Mu-dan. Compare on the application of EKF/UKF in satellite autonomous orbit determination using geomagnetic field[J]. Journal of Geomatics Science and Technology, 2011, 28(1): 50-53.
[8] 王向磊,赵东明. UKF在基于地磁场的自主导航中的应用分析[J]. 大地测量与地球动力学,2010,30(6):144-149.
WANG Xiang-lei, ZHAO Dong-ming. On application of UKF in autonomous navigation based on geomagnetic field[J]. Journal of Geodesy and Geodynamics, 2010, 30 (6): 144-149.
[9] Wu Jin-jie, Liu Kun, Wei Jing-bo, et al. Particle filter using a new resampling approach applied to LEO satellite autonomous orbit determination with a magnetometer[J]. Acta Astronautica, 2012, 81: 512-522.
[10] Cheon Yee-Jin. Fast convergence of orbit determination using geomagnetic field measurement in target pointing satellite[J]. Aerospace science and technology, 2013, 30: 315-322.
[11] Juang Jyh-Ching, Tsai Yung-Fu, Tasi Chiu-Teng. Design and verification of a magnetometer-based orbit determination and sensor calibration algorithm[J]. Aerospace Science and Technology, 2012, 21: 47-54.
Simplified geomagnetic orbit determination based on adaptive Kalman filter
YU Feng, HUA Bing, WU Yun-hua, KANG Guo-hua
(College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
Geomagnetic orbit determination is important for small satellites to realize low cost and high power/density ratio, but it has disadvantages such as large amount of calculation and insufficient precision due to various error sources. In this paper, a simplified state transition matrix is established based on the analysis of the orbital dynamics equation. In view that the geomagnetic gradient decreases significantly with higher order geomagnetic model, a simplified measurement equation with higher-order truncation is put forward. The complex magnetometer error is approximately modeled as random walk, and then a polynomial fitting method is employed to de-noise the magnetometer error estimate in real-time. The performance of the weak observable geomagnetic orbit determination is improved by an adaptive Kalman filter regulated by the magnetometer error variation characteristics which is identified from the de-noised estimate. Mathematical simulations verify the validity of the simplified geomagnetic orbit determination model, and the adaptive filter can more accurately achieve orbit calculation, in which the location and speed precisions are about 6 km and 4 m/s, respectively.
autonomous navigation; magnetic orbit determination; international geomagnetic reference field; adaptive Kalman filter
郁丰(1980—),男,副研究员,从事微小卫星控制技术、卫星导航研究。E-mail:yufeng@nuaa.edu.cn
1005-6734(2014)04-0519-06
10.13695/j.cnki.12-1222/o3.2014.04.018
V448.22+4
A
2014-04-15;
2014-07-30
国家自然科学基金(61203197,61203188);中国博士后科学基金(2013M531352)
