分布式POS传递对准对InSAR干涉测量影响的分析

朱庄生，郭 韬

（北京航空航天大学 惯性技术重点实验室 新型惯性仪表与导航系统技术国防重点学科实验室，北京 100191）

分布式POS传递对准对InSAR干涉测量影响的分析

朱庄生，郭 韬

（北京航空航天大学 惯性技术重点实验室 新型惯性仪表与导航系统技术国防重点学科实验室，北京 100191）

为了得到分布式POS在进行传递对准过程中由于大气扰动产生的挠曲变形姿态误差，以及这些误差与干涉式合成孔径雷达(InSAR)高程测量误差间的对应关系，提出了一种利用“速度+姿态”的传递对准方法，并利用它的误差来作为高程测量模型的输入，最后得出载机在传递对准过程中导致的高程测量误差。为了验证实验，搭建了分布式测量平台，针对该平台，首先根据机翼杆的挠曲变形运动模型增加载机y方向的变形角为Kalman滤波的状态变量，从而进行更精确的估计和补偿。然后推导了InSAR干涉测量的绝对误差表达式以及参数的选取。最后根据滤波结果和高度误差机理分析了横滚角误差对InSAR的高程信息产生的影响。通过仿真分析，传递对准得到的水平失准角误差小于0.009°，方位失准角误差小于0.015°，并且在横滚角误差为±0.089°时，高程误差小于4.2 m。

分布式POS；传递对准；InSAR；干涉测量

合成孔径雷达（SAR）是一种先进的微波对地观测设备，具有全天候、全天时工作的特点，对地面植被有一定穿透能力，能获得类似光学照片的目标图像，在航空遥感领域有着重要应用。随着科学技术的发展，航空遥感领域也提出了新的需求：

第一，需要解决雷达相对成像区域做非匀速直线运动时的成像问题，图1为载机做非匀速直线运动的示意图。众所周知SAR的理论分析都是建立在载机做匀速直线运动的情况下进行的，如果偏离理想运动情况，必须进行运动补偿。文献[19]分析了利用自聚焦算法进行运动补偿，文献[4]分析了利用POS数据进行运动补偿，但我们通过文献看出，目前的运动补偿技术仅仅是利用了POS的输出数据，假设它的输出是准确的，然后对SAR进行补偿，我们仍然不知道由分布式POS传递对准带来的误差对雷达的成像造成的影响。

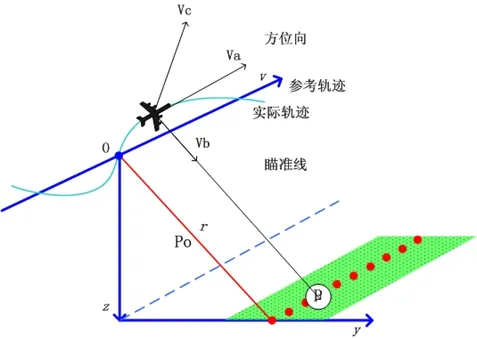
图1 载机真实航迹图Fig.1 The real flight track of the aircraft

图2 分布式SAR结构图Fig.2 The structure drawing of the distributed SAR

第二，需要解决高精度三维立体成像要求。InSAR的产生解决了测高的问题，它是由多个SAR雷达天线构成的遥感测量系统，图2给出了分布式SAR的结构图，它可以满足高分辨率对地观测系统检测高程信息的要求，但是遥感系统必须可以实时的检测到SAR天线相位中心的位置，做好运动补偿，而传统单一的POS系统无法精确地测出多个SAR天线的实时变化，所以必须由多个POS系统构成的分布式位置、姿态测量系统才可以实时的测量出SAR的精确位置、姿态信息用以补偿由于大气湍流或系统振动造成的机翼挠曲变形引起的误差。

由于分布式POS系统是由一个高精度主POS和若干中精度子POS组成，图3给出了实验搭建的分布式测量平台。所以必须使用传递对准技术来进行高精度惯导系统校正，这此过程中，由于机翼的振动必然会带来传递对准的误差。目前，在描述机翼挠曲变形建模时目前文献都采用二阶马尔科夫（Markov）模型，但模型需要的相关时间参数需要预先的经验值，不易于建模的通用与规范性。

图3 分布式POS地面演示系统实物图Fig.3 Photograph of the distributed POS ground-demo

本文分析的主要问题就是传递对准误差与干涉式合成孔径雷达高程信息测量间的关系。首先利用弹性力学理论进行挠曲运动的建模并加入到Kalman滤波中进行挠曲运动误差估计，增强了模型的可信度，参数可以通过规则计算唯一确定；然后把对准误差加入到 InSAR高程信息测量模型中，从而直观地分析分布式POS传递对准误差对InSAR测高的影响。

1 传递对准建模与仿真

分布式POS系统为了进行实时、高精度测量必须在分布载荷需要时进行动机座对准，也就是传递对准。它利用高精度主惯导的相对精确信息来作为子惯导系统的基准，利用主子惯导间的计算或量测差来反映子惯导的误差。根据量测量选择不同分为计算参数匹配和测量参数匹配，计算参数匹配包括速度、位置匹配；测量参数匹配包括角速率、姿态、加速度匹配。一般来讲，由于测量参数匹配法比较直接，其快速性优于计算参数匹配法，但对载体挠曲运动敏感，在同等条件下，其精度要低于计算参数匹配法。综合考虑，本文选用位置+姿态的传递对准方式。

1.1 分布式POS系统机翼模拟杆运动模型

根据弹性力学理论模态分析方法，机翼弯曲和扭曲变形可以由方程(1)描述：

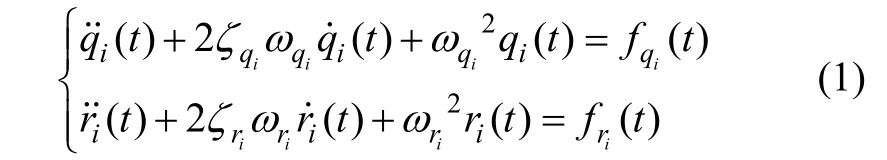
式中： ωqi、 ωri是模态频率（可用ANSYS模态分析得出）， ζqi、 ζri是模态阻尼系数（由机翼结构唯一确定）， fqi、 fri是广义外力（本文取为高斯白噪声）。

由于飞机颤振频率可达数十赫兹，而飞机收外部大气扰动的频率要小于飞机颤振频率，由挠曲变形角与弯曲、扭转位移的关系可知：

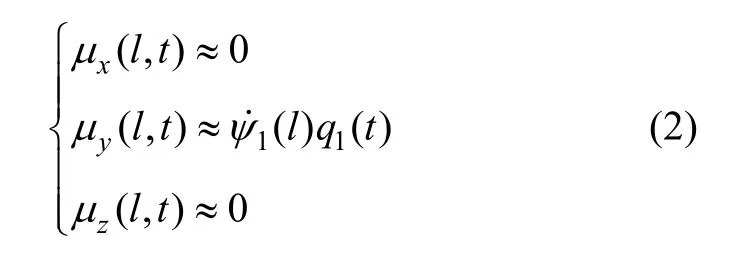
其中，ψ1(l)为模态形状函数。文献[6]用ANSYS进行了模态分析，可以看出，低频率扰动只需要分析弯曲变形，不用分析沿x轴方向的扭曲变形，所以本文只取第一阶模态，并且把由仿真得出的( l)曲线进行了拟合得到了表达式：

其中，α= -1.17，β=0.97，由于本文仿真用子POS的横向坐标l=1 m，所以结果如表1所示。

表1 拟合曲线参数表Tab.1 Fitting curve parameter table

本文主要分析沿y轴的弯曲位移，所以将式(3)的沿y轴变形角 μy(l,t)两边对t求取2阶导数：

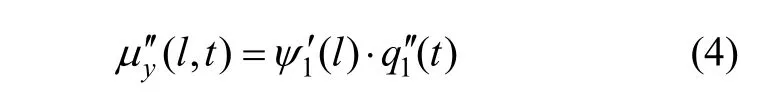
1.2 传递对准Kalman滤波方程

在高精度分布式 POS系统中需要使用传递对准技术来实现IMU系统的初始对准，对准过程分为两个阶段，即粗对准和精对准，粗对准过程是把高精度主惯导信息直接传输给子惯导并作为子惯导导航参数初始值，而精对准则需要利用 Kalman滤波技术来估计出对应的误差信息然后进行补偿，下面主要讲的是精对准过程的Kalman滤波方程的选取。

1.2.1 状态方程的建立

本文的Kalman滤波仿真是假设主POS导航参数精确，来模拟子POS的误差参数，所以暂且不加入GPS的组合参数，在实际建模中需要主POS的组合导航结果来对子POS进行传递对准。具体误差模型如下：

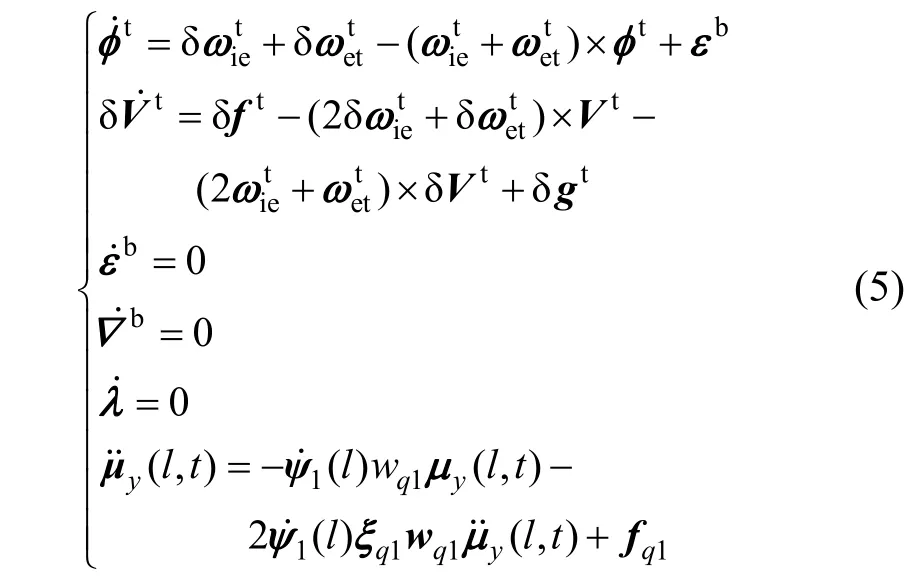
式中，φt为惯导系统的失准角，是地球坐标系相对惯性坐标系的角速度误差，是地理坐标系相对地球坐标系的角速度误差，εb是陀螺仪的漂移，是主、子POS间的速度误差， δft是主、子POS间的测量比力误差， δgt是重力加速度的误差，▽b是加速度计的常值偏置，λ为安装误差角。系统状态方程为：

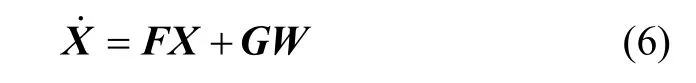
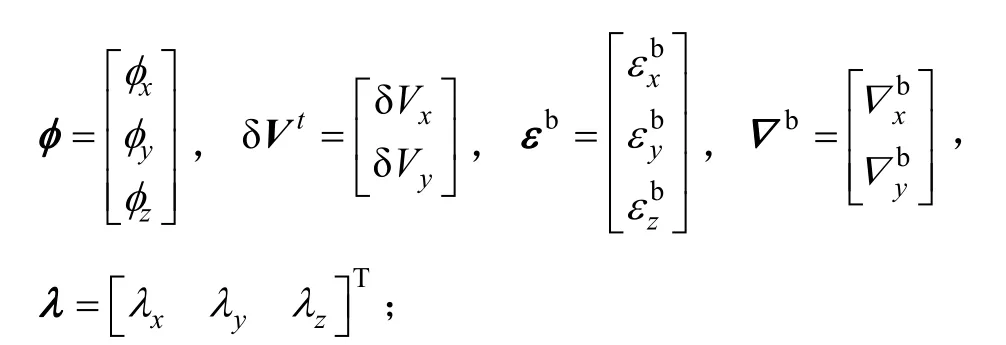
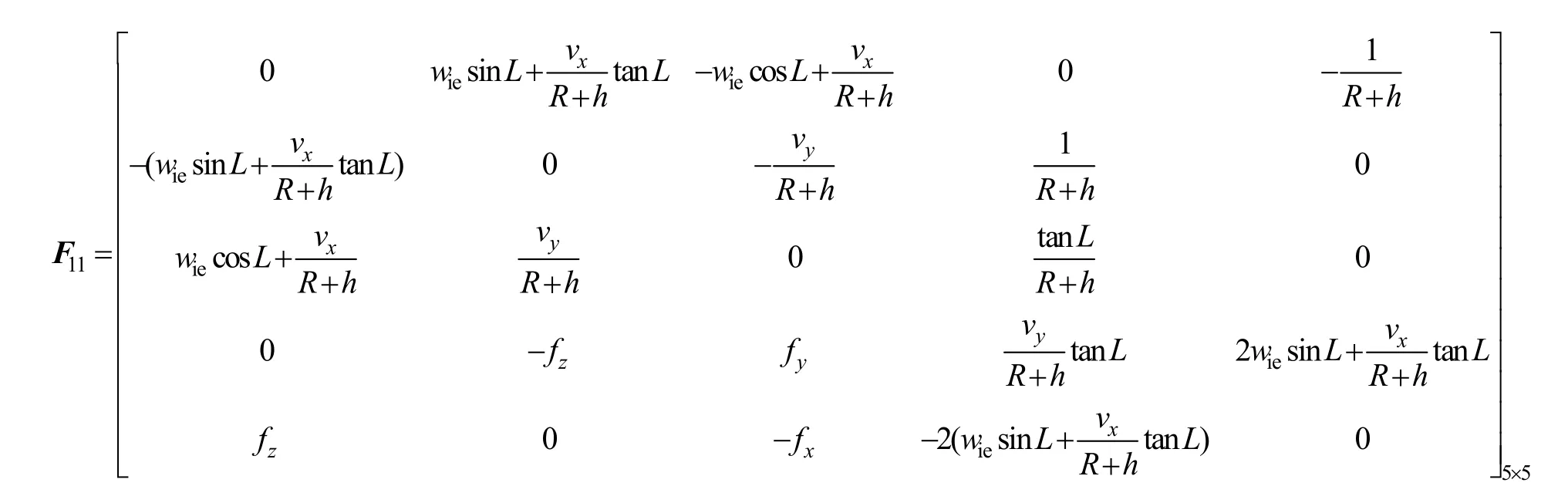
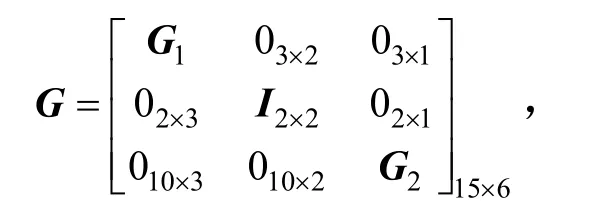
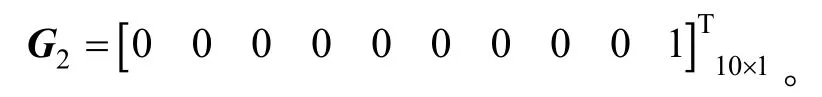
1.2.1 量测方程的建立

本文采用的是速度+姿态的匹配方式，所以量测量有5个，分别是3个主、子POS的姿态角的差和2个主、子POS的速度差，具体如下：

其中，H是量测矩阵，

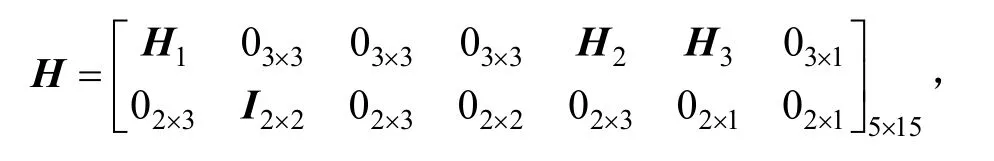
具体参数参看文献[12]。

1.3 传递对准仿真条件及结果

1.3.1 仿真条件

本文选用的POS数据是U型轨迹数据，航向角一共变化了180°，飞行速度为100 m/s，实验采用轨迹发生器来产生惯性器件的原始数据再利用 Matlab将得到的惯性器件数据叠加相应大小的噪声，作为仿真使用的数据，图4为仿真轨迹。

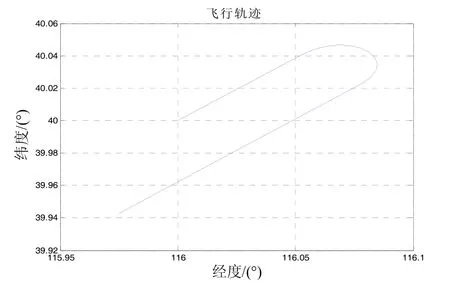
图4 仿真飞行轨迹图Fig. 4 Flight track by the simulation

飞行参数：飞行高度为3000 m，初始经度116，初始纬度40，初始速度为0，初始俯仰角、横滚角、航向角为[0° 0° 45°]。

器件参数：陀螺仪随机漂移为0.01°/h，陀螺仪常值漂移为0.02°/h，加速度计随机误差为50 μg，加速度计常值偏置为100 μg。

1.3.2 仿真结果

首先通过 Kalman滤波估计出了姿态角误差，如图5所示。图6为安装角误差估计。通过增加的Kalman滤波状态变量估计出的沿y方向的挠曲变形角及真实的变形角对比曲线如图7所示。

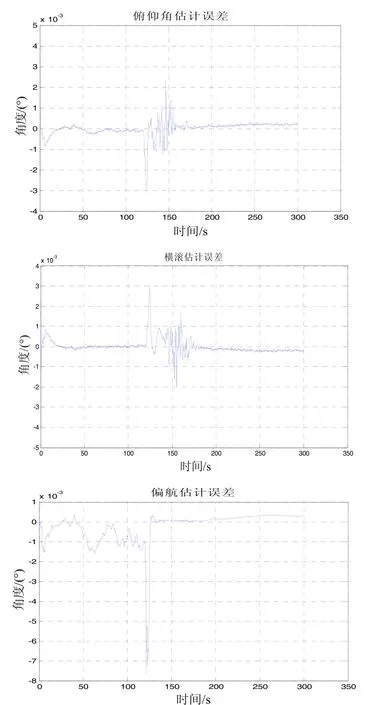
图5 姿态角误差估计曲线Fig.5 The estimation of attitude angle

通过仿真结果可以看出，飞行模拟数据共300 s，在120～170 s间，安装误差角和姿态误差的估计值产生大幅值波动，这是由于180°的大角度机动导致，不过在机动转弯后，曲线恢复收敛，且x、y轴姿态角估计误差均值为 0.009°；安装误差角估计误差均值为0.13°，z轴姿态角估计误差均值为0.015°；安装误差角估计误差均值为0.23°。而通过挠曲变形角估计图可明显看出采用“速度+姿态”匹配方式的传递对准方法可以有效地估计出机翼挠曲变形角，且估计精度为0.18°。

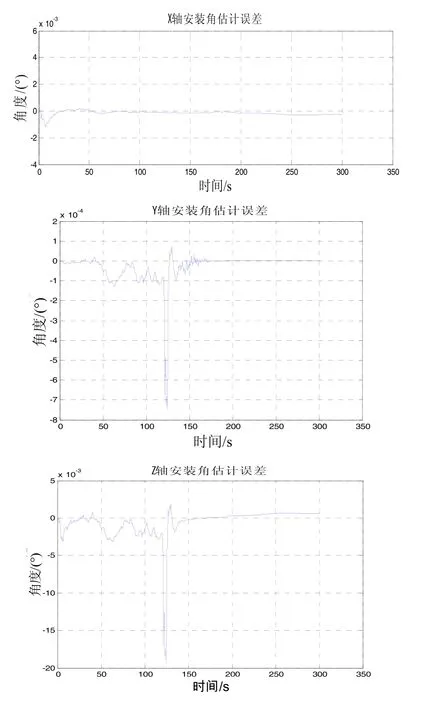
图6 安装角误差估计曲线Fig.6 The estimation of fixed error angle

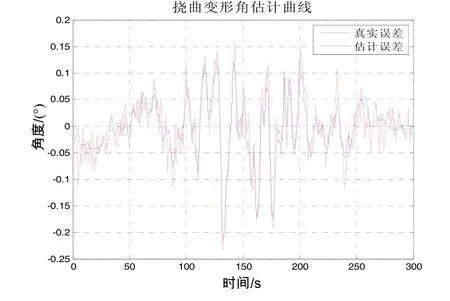
图7 挠曲变形角估计曲线Fig.7 The estimation of elastic flexure angle

2 InSAR测高原理及误差分析

高度测量大致分为两种方式：一种是对同一目标用SAR在不同高度飞过两次，此法称为单天线双航过法；另一种是在SAR上面装两个不同高度的天线，主天线即发送信号又接收信号，而副天线只接收信号，由于两个天线离目标的距离有差异，因此信号相位不同，会产生相位差，这种方法称为双天线单航过法。

对于机载SAR而言，双天线的间距仅仅需要1～2 m，因此在用于机载时往往采用双天线单航过法，同时这种方法大大提高了测量精度。

2.1 分布式SAR系统高程信息测量原理

如图8所示，载机上装有天线A与天线B，两天线夹角为α，两天线间的长度为m，雷达波长为λ，目标高度为h，载机高度为H。则两天线对目标信号接收到的相位差为：

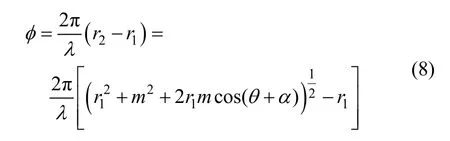
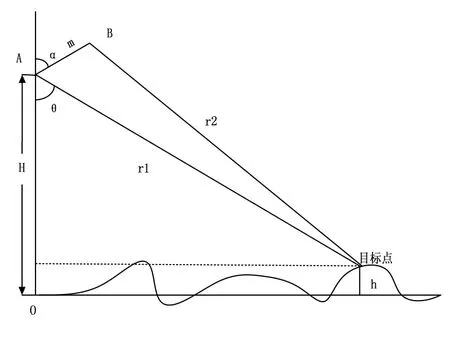
图8 干涉测量原理图Fig.8 Schematic of interferometric measurement

此时，相位差φ 可以是 φ= φ'+ 2πn，φ'值可以由SAR的测相设备测得，如果能设计m使上式中n= 0，则 φ= φ'就可以直接得到相位差而不必求n。由于天线A既发送又接收，因此可以测得r1值，而且由于m、α、λ全是已知参数，H可以从飞机的测高设备获得，所以可做推导如下：

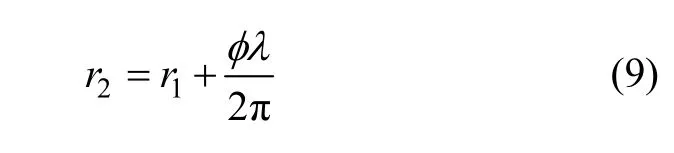
由图8几何关系可得：

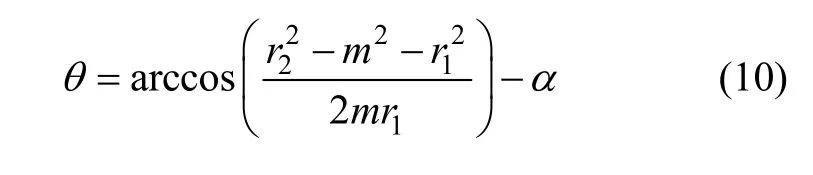
于是可得最终高度：

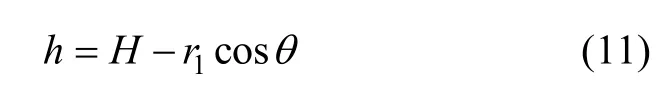
2.2 高程信息误差分析

造成高度误差的因素多种多样，典型的有横滚角误差eα；GPS/INS组合导航高度误差 eH，天线与散射点位置误差 er1；基线误差 em；相位误差eφ；雷达波段测量误差eλ等等，每一项所代表的含义不同，它们对整个高程测量误差的贡献程度也不同，所以下面给出高度测量绝对误差表达式：

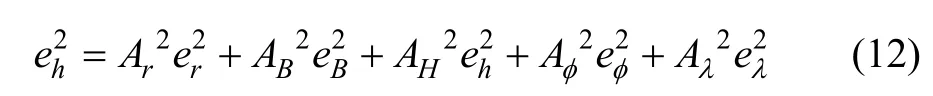
由于每一项误差源对高程测量的结果作用大小不同，所以需要确定出绝对误差式中各自误差项的系数A，在双天线单航过模式中，假设各误差统计独立，具体计算如下：

2.3 横滚角误差与测高误差仿真分析

在测高分析中可知影响高程精度的因素中，POS系统可以产生两种误差，一种是 GPS/INS组合导航时产生的飞机高度测量误差，另一种是由于POS系统测量的横滚角有误差会直接造成α的误差，从而影响高程精度。由于高度误差是直接作用于高程测量结果的，具有一一对应关系，所以在此我们不做仿真分析，本文着重分析一下传递对准后的横滚角误差造成的高程信息误差。

2.3.1 仿真条件

本次仿真取基线长度m=1，选用X波段合成孔径雷达条件，波长λ=0.052 m，α=0°，飞行高度在3 km，通过测高原理导出高度曲线。

2.3.2 仿真结果

由于本次仿真采用轨迹发生器产生了一组U型轨迹数据，所以可以得到飞行数据的真实值，通过比对传递对准估计出的横滚角误差和轨迹发生器的真实值，我们可以清楚地得到传递对准后的横滚角角估计误差，如图9所示。

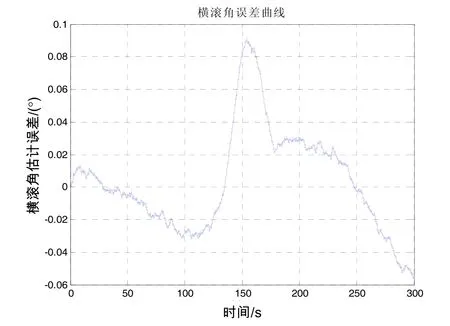
图9 横滚角估计误差曲线Fig.9 The estimated error of the roll angle

通过上面的高程误差分析后，我们知道如何在已知横滚角误差情况下导出对应的高程误差关系，本次采用横滚角误差作为输入，通过高程绝对误差式导出以POS为误差源产生的高程误差，仿真结果如图10所示。

观察横滚角估计值的误差曲线，可以看出横滚角误差精度为0.089°，在此条件下，机载双天线SAR的测高精度可以达到4.2 m。

图10 高度误差曲线Fig.10 The altitude error curve

3 结 论

本文研究了传递对准造成的横滚角误差对InSAR高程测量的影响。首先，提出了一种“速度+姿态”的传递对准方法并进行了U形轨迹仿真分析，得到了传递对准的分析结果，并且与真实值比对得到对准误差。然后给出了机载双天线合成孔径雷达的干涉测高原理，在此基础之上建立了干涉测高的高程绝对误差表达式，给出了其中的参数推导过程。最后，将传递对准误差输入到绝对误差式中进行仿真分析，给出了传递对准中横滚角误差对高程测量的影响曲线，对今后的POS数据运动补偿分析打下了基础。

仿真结果表明，“速度+姿态”的传递对准可以有效地估计出挠曲变形角，并且通过高程绝对误差式仿真出最终对高程精度可达到4.2 m。

（References）：

[1] Luan Hongzhong, Mao Yuliang. Study on a method of rapid transfer alignment[C]//Proceeding of the 2nd International Conference on Intelligent Control and Information Processing. 2011: 204-207.

[2] Feng Zhihua, Jiang Weiwei, Gao Shengsheng. Research of rapid transfer alignment and observability analysis[C] //Proceeding of the 2011 International Conference on Mechatronic Science, Electric Engineering and Computer. 2011: 204-207.

[3] 李芳芳，仇晓兰，孟大地，等. 机载双天线 InSAR 运动补偿误差的影响分析[J]. 电子与信息学报，2013，35(3)：559-567.

LI Fang-fang, QIU Xiao-lan, MENG Da-di, et al. Effect of motion compensation error on performance of airborne dual-antenna InSAR[J]. Journal of Electronics & Information Technology, 2013, 35(3): 559-567.

[4] 韦立登，向茂生，吴一戎. POS 数据在机载干涉 SAR运动补偿中的应用[J]. 遥感技术与应用, 2007, 22(2): 188-194.

WEI Li-deng, Xiang MAO-sheng, WU Yi-rong. The application of the data of POS in airborne SAR motion compensation interference[J]. Remote Sensing Technology and Application, 2007, 22(2): 188-194.

[5] 何峰，梁甸农，刘建平. 星载双基地 SAR 干涉测高误差分析[J]. 系统工程与电子技术，2005，27(9)：1519-1522.

HE Feng, LIANG Dian-nong, LIU Jian-ping. Analysis on the height measurement error of spaceborne bistatic SAR interfermetry[J]. System Engineering and Electronics, 2005, 27(9): 1519-1522.

[6] 房建成，张舟，宫晓琳. 机载分布式 POS 传递对准建模与仿真[J]. 中国惯性技术学报, 2012, 20(4): 379-385.

FANG Jian-cheng, ZHANG Zhou, GONG Xiao-lin. Modeling and simulation of transfer alignment for the distributed POS[J]. Journal of Chinese Inertial Technology, 2012, 20(4): 379-385.

[7] Jones D, Roberts C, Tarrant D, et al. Transfer Alignment Design and Evaluation Environment[C]//Proceeding of the IEEE Regional Conference on Aerospace Control Systems. 1993: 753-757.

[8] Majeed S, Fang Jiancheng. Performance improvement of angular rate matching shipboard transfer alignment[C]// Proceeding of the 9th International Conference on Electronic Measurement & Instruments. 2009: 3-706～3-711.

[9] Sun Changyue, Deng Zhenglong. Transfer alignment of shipborne inertial-guided weapon systems[J]. Journal of Systems Engineering and Electronics, 2009, 20(2): 348-353.

[10] 陈大伟，杨国伟. 静气动弹性计算方法研究[J]. 力学学报，2009，41(4)：469-479.

CHEN Da-wei, YANG Guo-wei. Static Aeroelastic analysis of a flying-wing using different models[J]. Journal of Mechanics, 2009, 41(4): 469-479.

[11] Arthut A, Sutherland J R. The Kalman filter in transfer alignment of inertial guidance systems[J]. Journal of Spacecraft, 1968, 5(10): 1175-1180.

[12] Chen Kai, Zhao Gang, Meng Zhongjie, Yan Jie, Lu Hao. Equivalent approaches to equations of traditional transfer alignment and rapid transfer alignment[C]// Proceeding of the 7th World Congress on Intelligent Control and Automation. 2008: 204-207.

[13] Shen Xiaorong, Shi Yongzhu. Angular rate matching method for shipboard transfer alignment based on H∞filter[C]//Proceeding of the IEEE Conference on Industrial Electronics and Applications. 2011: 620-625.

Effect of distributed POS transfer alignment on InSAR interferometic measurement

ZHU Zhuang-sheng, GUO Tao
(Key Laboratory of Fundamental Science for National Defense-Novel Inertial Instrument & Navigation System Technology, Science & Technology on Inertial Laboratory, Beihang University, Beijing 100191, China)

In order to get the flexural angel error caused by distributed POS due to atmospheric disturbances and find this error’s corresponding relationship with the altitude error caused by interferometric synthetic aperture radar(InSAR), a transfer alignment method using the "velocity + attitude" matching algorithm was proposed. Then the error of the estimation is used as the input parameter of the height measurement model to obtained the altitude error caused during transfer alignment. A distributed measurement platform was built to verify the experiment, and the following analyses were made about the platform: 1) according to the motion model of the flexural wings, the flexural angel in y coordinate axis was added to the Kalman filter’s state variables; 2) the absolute error expressions of InSAR interferometry measurement and the method of selecting the parameters was deduced; 3) according to the filtering results and the mechanism of altitude measurement, the roll angel error’s influence on InSAR altitude information was analyzed. The simulation results show that the horizontal and azimuth misalignments by the proposed method are superior to 0.009° and 0.015° respectively, and when the roll angel error is within ±0.089°, the altitude error is less than 4.2 m.

distributed POS; transfer alignment; InSAR; interferometry measurement

朱庄生（1972—），男，副教授，硕士生导师。E-mail：zszhu@buaa.edu.cn

1005-6734(2014)04-0432-07

10.13695/j.cnki.12-1222/o3.2014.04.003

U666.1

A

2014-02-19；

2014-05-15

国家重大科学仪器设备开发专项项目（2012YQ160185）