Fast alignment algorithm of inertial fixed frame in quasi-static environment

LIU Xue-jun, LI Yong-tao

(China Huayin Ordnance Test Center, Huayin 714200, China)

Fast alignment algorithm of inertial fixed frame in quasi-static environment

LIU Xue-jun, LI Yong-tao

(China Huayin Ordnance Test Center, Huayin 714200, China)

An initial alignment is needed to determine the initial attitude when inertial navigation system(INS) start to work. In this paper, an inertial fixed frame fast(IF3) alignment algorithm is devised, in contrast to the classic alignment algorithms, such as gyrocompassing and Kalman filtering techniques. Unlike classic techniques, the IF3alignment is effective with any initial attitude error, as well as high frequency vibrations. The estimator is based on decomposing the attitude matrix into separate earth motion, inertial rate, and alignment matrix. And the alignment matrix is determined by two sets of observation vectors in different inertial fixed frames. By smooth pre-filtering, interleaved sampling and double integrating the observation vectors, it is shown that the precision of attitude estimates is improved. The IF3alignment heading error is less than 1 mil(1σ) within 60 s, 0.6 mil(1σ) within 180 s, and 0.4 mil(1σ) within 300 s under the condition that the vehicle engine is running at idle and intended introducing the perturbation caused by a person’s getting on and off the vehicle. Experiment tests favorably demonstrate its rapidness, accuracy and robustness.

inertial fixed frame fast alignment; smooth pre-filtering; interleaved sampling; multiple integral

Strapdown inertial navigation system(SINS) is a system which calculates velocity by integrating the total acceleration and computes position by integrating the resultant velocity. The initial alignment is of great importance for any SINS, because the performance of the INS is largely decided by the accuracy and rapidness of the alignment process. The classic alignment methods are typically composed of two steps, a coarse alignment phase, followed by a fine alignment phase. Typically, the coarse alignment phase is required to estimate the vehicle’s heading to within a few degrees and pitch/roll to within a few tenths of a degree to allow the fine alignment filter to operate within its linear region. The coarse alignment is often realized by using the analytic method which regards the initial attitude as constant, but the real time attitude is time-varying due to the vibration introduced by the started engine and person getting on and off the vehicle. It needs to be refined by gyrocompass or Kalman filtering methods. The gyro-compassing and Kalman filtering techniques are founded on the simplified linear system models. As a result of model simplification, the alignment performance is compromised, e.g., slow convergence and vulnerability to disturbances[1].

This paper is dedicated to the IF3alignment algorithm. No model simplification has been made throughout the derivation and it has such benefits as rapidness, accuracy and robustness. It does not need a parameter-tuning process that is inevitable for either gyrocompassing(pole placement) or Kalman filtering (error covariance predetermination and small initial value) method. The main contribution of this paper is a new way of thought to address the INS alignment, besides the gyrocompassing and filtering methods. The SINS alignment requires determining the time-varying attitude in real time. The decomposition of attitude matrix into separate earth motion, inertial rate, and alignment matrix makes the SINS alignment transformed into a problem of determining the initial attitude at the very start point of alignment that is a constant quantity. It is solved by using the dual-vector attitude determination algorithm[3].

1 General alignment algorithm derivation

1.1 Reference frames.

The coordinate frames used in this paper are defined as follows:

i-frame: Earth-centered initially fixed(ECIF) orthogonal reference frame.

e-frame: Earth-centered earth-fixed(ECEF) orthogonal reference frame.

n-frame: Orthogonal reference frame aligned with East-North-Up(ENU) geodetic axes.

b-frame: Orthogonal reference frame aligned Inertial measurement unit(IMU) axes.

i0-frame: Orthogonal reference frame non-rotating relative to the i-frame. It is formed by fixing the n-frame at the initial inertial space.

e0-frame: Orthogonal reference frame non-rotating relative to the i-frame. It is formed by fixing the e-frame at the initial inertial space.

n0-frame: n-frame at the start-up. It is rotating with the Earth.

ib0-frame:Orthogonal reference frame non-rotating relative to the i-frame. It is formed by fixing the b-frame at the initial inertial space.

1.2 Decomposition of the attitude matrix

The attitude matrix, which relates the b-frame to the n-frame, can be decomposed as follows:

where[4]

where ωieis the turn rate of the Earth.

The rotation matrix of the b-frame relative to the- framecan be calculated using the gyro output. At the beginning of the initial alignment,is identical with:

where I3×3is a 3×3 identity matrix. Subsequent orientation ofis updated by the gyro output:

1.3 Estimation of the alignment matrix

In the n-frame, there exits:

In the quasi-static situation, we assume that vn（t）=（ t）=0, Eq.(5) changes into:

Reorganizing the terms yield:

Define two vectors as follows:

We can estimate the alignment matrixby using the dual-vector attitude determination algorithm as follows:

wheret1＜ t2.

2 Improvements of the IF3 alignment algorithm

The IF3alignment algorithm made three improvements focusing on the weaknesses of the general alignment algorithm described in the previous section. In the real working environment, the hypothesis vn（t）=（t）=0 is no longer valid because of the vibration noise induced by the engine working and a person getting on and off. Ignored the second order term, Eq.(5) is changed into

With the translation vibration interfering, the acceleration measurement contains two kinds of signals defined as follows:

Substituting Eq. (16) and (17) into Eq. (15) yields:

Substituting Eq. (12), (13) and (16) into Eq. (11) yields:

where

Integrating Eq. (19) over ［t0, t］ yields:

Integrating Eq. (20) yields:

In order to improve the accuracy of the estimated alignment matrix, three techniques are applied to the IF3alignment algorithm:

a) smooth pre-filtering

The smooth pre-filtering is a kind of noise suppressor.（t ）can be reduced in the acceleration measurements. This advantage can reduce the attitude estimate random error with very little computation throughput.

b) multiple integral

It is shown in the Eq. (20) that the velocity at the two time points is the main error resource for the attitude estimate error. Throughout the multiple integral technique, the term of（t） is vanished, because（t） is a kind of high frequency random error.

c) interleaved sampling

For the case of quasi-static alignment, the covariance of the attitude estimate is a function of the variance of navigation frame velocity disturbances. It is shown that, by interleaving the velocity vectors, the resulting attitude estimate is improved over sequential sampling techniques[7].

3 Test results

The presented IF3alignment algorithm was applied to a real quasi-static data collected about 3000 s from a navigation grade IMU at latitude 39.17°N. The IMU consists of three ring laser gyroscopes with a drift rate of 0.01 (°)/h (1σ) and three quartz accelerometers with bias of 50 μg (1σ). The IMU is on a vehicle with its engine working and a person getting on and off it. The amplitude of the roll varies from 0 to 6 mil. Fig.1 shows the yaw errors of 50 IF3alignments in which each alignment lasts less than 60 s. The accuracy of the alignments is about 0.75 mil(1σ). Fig.2 shows a particular yaw estimation curve during the alignment. Fig.3 shows the yaw errors of 25 IF3alignments in which each alignment lasts less than 120 s. The accuracy of the alignments is about 0.54 mil (1σ). Fig.4 shows a particular yaw estimation curve during the alignment. Fig.5 shows the yaw errors of 16 IF3alignments in which each alignment lasts less than 180 s. The accuracy of the alignments is about 0.37 mil(1σ). Fig.6 shows a particular yaw estimation curve during the alignment.

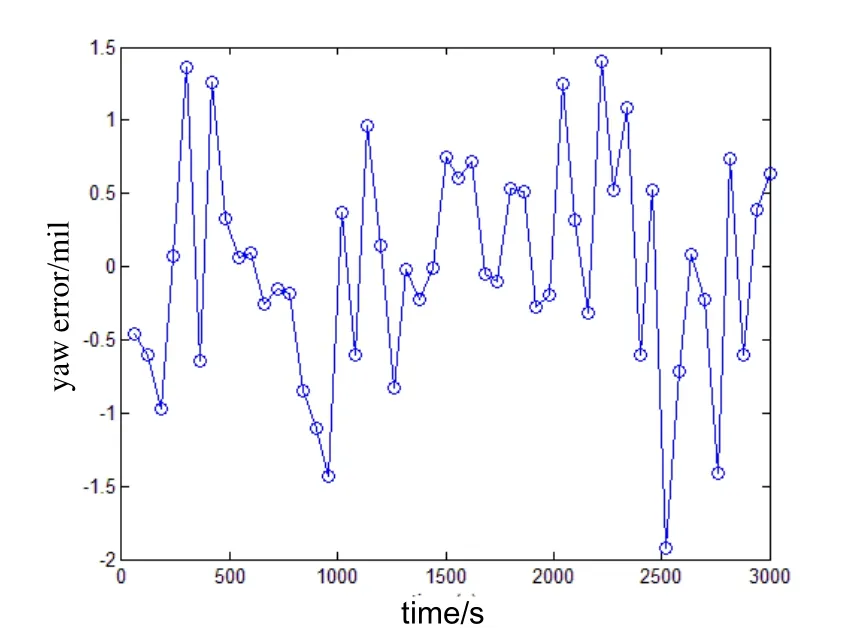
Fig.1 Yaw errors 60 s in IF3 alignments

The accuracy of roll and pitch estimate errors are less than 0.1 mil during all the three kinds of IF3alignments.

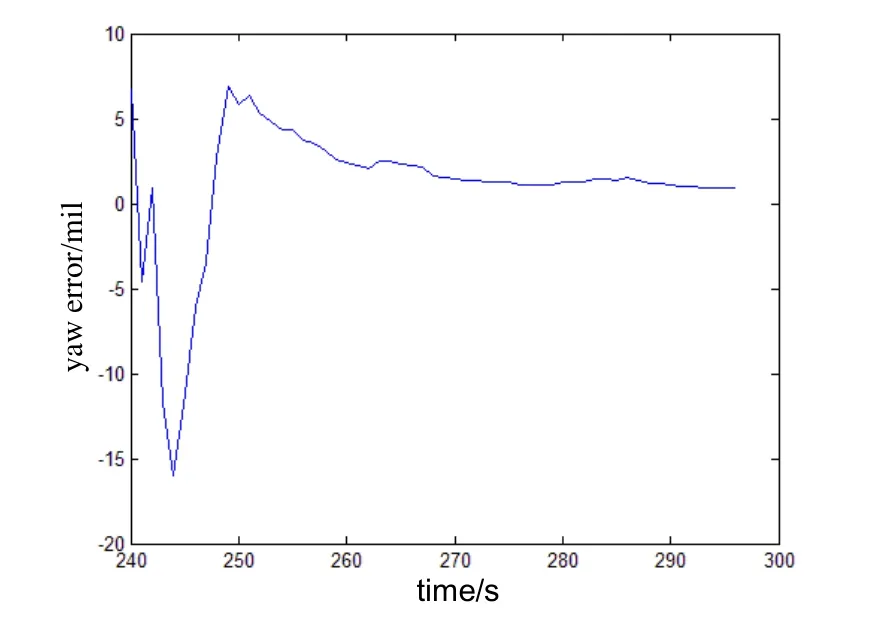
Fig.2 Yaw estimation curve in 60 s IF3 alignment

Fig.3 Yaw errors in 120 s IF3 alignments

Fig.4 Yaw estimation curve in 120 s IF3 alignment

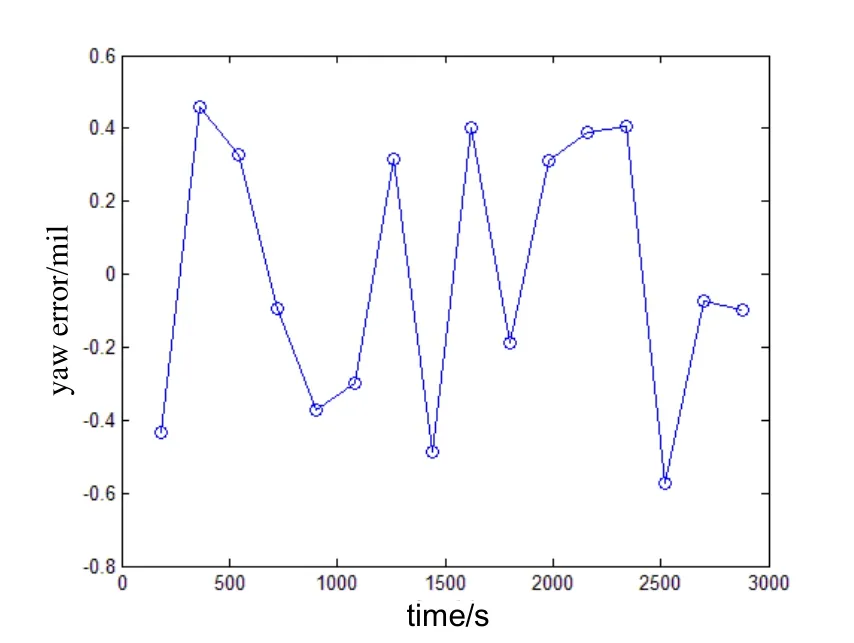
Fig.5 Yaw errors in 180 s IF3 alignments

Fig.6 Yaw estimation curve in 180 s IF3 alignment

4 Conclusions

Experiment results favorably demonstrate the rapidness, accuracy and robustness of the IF3alignment algorithm. In quasi-static environment, the vehicle is influenced by angular motions and translational motions. With the help of smooth pre-filter, multiple integral and interleaved sampling techniques, the IF3alignment algorithm is able to satisfactorily cope with angular/ translational motions in the experiments. The classic alignment approaches such as Kalman filter and gyrocompass were not liable to be disturbed by angular motions and performed very poorly. The proposed algorithms have been successfully applied to real INS systems and work well.

Reference:

[1] Titterton D H, Weston J L. Strapdown inertial navigation technology[M]. 2nd ed., IEE, 2004.

[2] Choukroun D. Novel methods for attitude determination using vector observations[D]. Haifa: Technion-Israel Institute of Technology, 2003.

[3] YAN Gong-min. On SINS in-movement initial alignment and some other problems[D]. Xi’an, China: Northwestern Polytechnic University, 2008.

严恭敏. 捷联惯导系统动基座初始对准及其其它相关问题研究[D]. 西安：西北工业大学，2008.

[4] Wu Y, Pan X. Velocity/position integration formula (I): Application to in-flight coarse alignment[J]. IEEE Transactions on Aerospace Electronics System, 2013, 49: 1006-1023.

[5] Han S, Wang J. A novel initial alignment scheme for low-cost INS aided by GPS for land vehicle applications [J]. Journal of Navigation, 2010, 63: 663-680.

[6] Silson P M G. Coarse alignment of a ship’s strapdown inertial attitude reference system using velocity loci[J]. IEEE Transactions on Instrumentation and Measurement 2011, 60(6): 1930-1941.

[7] Gu D, El-Sheimy N, Hassan T, Syed Z. Coarse alignment for marine SINS using gravity in the inertial frame as a reference[C]//Proceedings of Position, Location and Navigation Symposium, 2008: 961-965.

[8] Li W, Wu W, Wang J, Lu L. A fast SINS initial alignment scheme for underwater vehicle applications[J]. Journal of Navigation, 2013, 66: 181-198.

[9] WANG Qing-zhe, FU Meng-yin, XIAO Xuan, et al. Rapid transfer alignment method based on inertial reference frame[J]. Journal of Chinese Inertial Technology, 2012, 20(2): 168-172.

王清哲，付梦印，肖烜，等. 基于惯性参考系基准的快速传递对准方法[J]. 中国惯性技术学报，2012, 20(2): 168-172.

1005-6734(2014)04-0459-04.5

10.13695/j.cnki.12-1222/o3.2014.04.007

伪静态环境凝固惯性系快速对准算法

刘学俊，李永涛

（中国华阴兵器试验训练中心，华阴 741200）

惯性导航系统在开始工作时需要进行初始对准从而确定初始姿态。提出了一种与经典的对准算法如陀螺罗经或卡尔曼滤波技术不同的凝固惯性系快速（IF3）对准算法。可在任意初始误差条件下进行对准，且能适应高频扰动环境。将姿态矩阵分解成地球自转、惯性速率和对准矩阵三个部分。对准矩阵依靠两组分别处于不同惯性系里的观测向量确定。通过采用前置平滑滤波、层叠采样和二重积分技术，对准精度显著改善。在载车发动机怠速运行和人员上下车扰动条件下，60 s对准误差优于1 mil (1σ)，180 s对准误差优于0.6 mil(1σ)，300 s对准误差优于0.4 mil(1σ)。实验结果证明了IF3对准算法的快速性、准确性和鲁棒性。

凝固惯性系快速对准；前置平滑滤波；层叠采样；多重积分

U666.1

A

2014-01-21；

2014-05-05

国防重点预研项目（51309010303）

刘学俊（1980— ），男，工程师，研究方向为光电测量技术。Email：lewxuejun@163.com