一种激光陀螺惯性测量单元混合标定方法

程骏超，房建成，吴伟仁，李建利，王文建

（北京航空航天大学 新型惯性仪表与导航系统技术国防重点学科实验室，北京 100191）

一种激光陀螺惯性测量单元混合标定方法

程骏超，房建成，吴伟仁，李建利，王文建

（北京航空航天大学 新型惯性仪表与导航系统技术国防重点学科实验室，北京 100191）

针对采用低精度转台标定高精度激光陀螺惯性测量单元(IMU)的方法进行了研究。提出一种不依赖转台精度的静态解析与Kalman滤波估计混合的新型高精度标定方法。首先采用多位置静态解析法粗标定出IMU系统参数的低精度初始值；然后根据惯性导航算法基本误差方程，建立以IMU系统参数粗标定结果的残差为估计对象，以IMU速度误差为观测量的扩展Kalman滤波器，估计出系统参数残差，进一步修正粗标定结果。实验结果表明，该方法能够利用低精度转台获得与高精度转台相当的参数标定精度，降低了惯导系统的标定成本，满足高精度激光陀螺IMU的使用需求。

机抖激光陀螺；惯性测量单元；混合标定；误差补偿；Kalman滤波

激光陀螺具有精度高、启动快、数字化输出等优点[1]，由其组成的惯性测量单元（Inertial Measurement Unit, IMU）已被广泛应用于航空、航海及遥感测绘等领域[2-3]。然而，IMU的性能直接由其系统参数标定的精度决定[3-4]，高精度激光陀螺 IMU通常需要使用价格昂贵的高精度精密转台才能标定，无形中增加了IMU的生产成本。因此，如何使用低精度转台标定高精度激光陀螺IMU，降低标定成本，保证标定精度，成为亟待解决的问题。

IMU系统参数标定是指获取外部运动激励与IMU输出信号之间解析关系的过程，国内外已有大量文献开展了研究。传统的静态多位置与动态角运动相结合的标定方法[3-6]需要精密转台提供精确的姿态和角速率基准，基于敏感分量对称相抵的思想获得标定结果。然而，该方法标定结果的精度严重依赖于转台的角位置、角速率、调平以及指北精度[4]，而标定高精度机抖激光陀螺IMU的要求更为苛刻。

近年来，Syed等人提出一种所谓“shape-frommotion”思想的IMU静态多位置标定方法[7-8]，该方法基于输入激励与 IMU输出信号模相等的基本原则，无需转台提供任何基准，即可直接标定出所有IMU系统参数。然而，其角速度通道系数精度较低，无法满足高精度机抖激光陀螺 IMU的使用需求[8]。此外，学者们还提出了基于Kalman滤波的系统级标定方法[9-11]，它以惯导误差方程为基础建立滤波模型，以速度误差为观测量，在IMU运动过程中估计IMU系统参数。该方法虽然不依赖精密转台，但对系统参数直接进行估计，精度通常受滤波器稳定性的影响，收敛速度较慢[10]。

综合上述各方法优缺点，本文提出一种激光陀螺IMU混合标定新方法，具体分为三步：首先采用基于“shape-from-motion”思想的解析方法标定出IMU系统参数低精度初始值；然后从惯导误差方程出发，建立以IMU系统参数粗标定结果的残差为状态变量，以速度误差为观测量的扩展kalman滤波器，估计系统参数残差；最后利用残差修正初始值，得到IMU系统参数高精度标定结果。该方法无需精密转台提供姿态基准，降低了标定成本，保证了标定精度。最终，本文通过实验结果证明了提出方法的有效性。

1 IMU系统参数粗标定

1.1 IMU测量模型

假设正交IMU机体系o-xbybzb为b系，三支陀螺仪敏感轴确定的非正交坐标系o-xgygzg为g系，三支加速度计敏感轴确定的非正交坐标系 o-xayaza为 a系。IMU加速度通道的测量模型可表示为[8]：

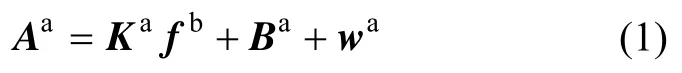
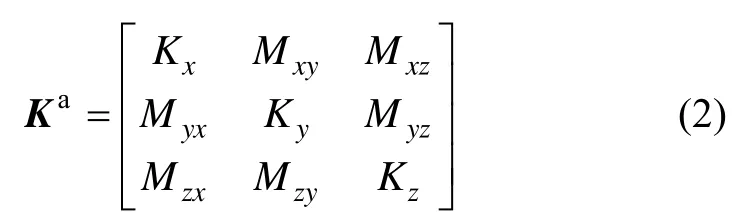
式中， Ki(i = x,y,z)表示i方向加速度计的标度因数，Mij(i, j = x,y,z;i ≠ j)表示a系下i方向加计测量轴与b系下j轴的安装系数。定义b系下xb轴与xa轴重合，yb轴在o-xaya平面内垂直于xb，zb轴与xb和yb符合右手定则。那么式(2)可以变成：

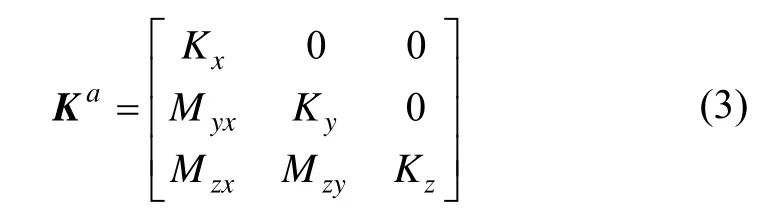
同理，IMU角速度通道测量模型可表示为[4]：

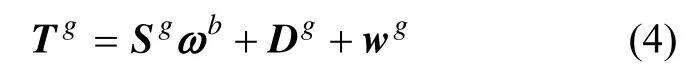
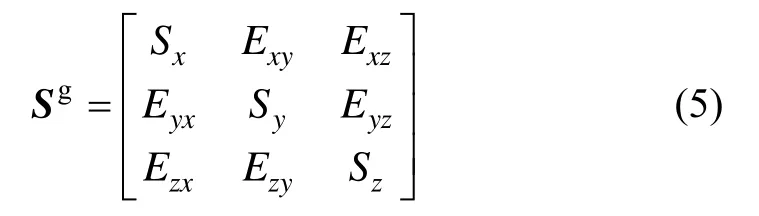
式中， Si(i = x,y,z)表示i方向陀螺的标度因数，Eij(i, j = x,y,z;i ≠ j )表示g系下i方向陀螺测量轴与b系下j轴的安装系数。

1.2 IMU系统参数粗标定

“Shape-from-motion”的基本思想是利用外部激励与 IMU输出量模相等的原则建立系统参数标定的数学关系，本文利用该方法实现IMU系统参数粗标定。

1.2.1 加速度通道粗标定

加速度通道的测量模型式(1)可进一步写成：

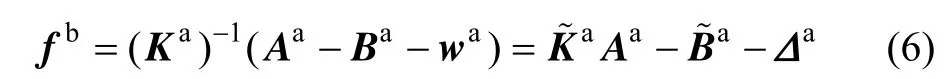
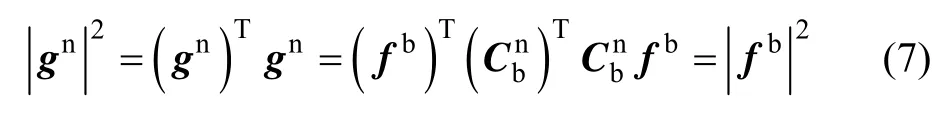
通过长时间采样求平均的方法消除随机误差因素Δa的影响，并将式(6)带入式(7)中，则：

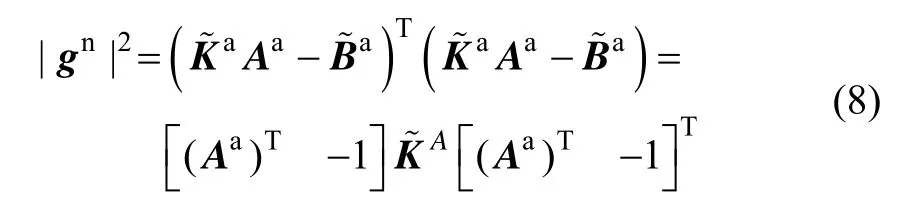
式中：

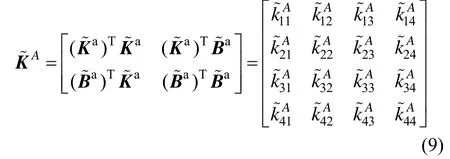
是由加速度通道所有待求参数构成的对称矩阵，将式(9)带入式(8)，并将其展开为线性形式：

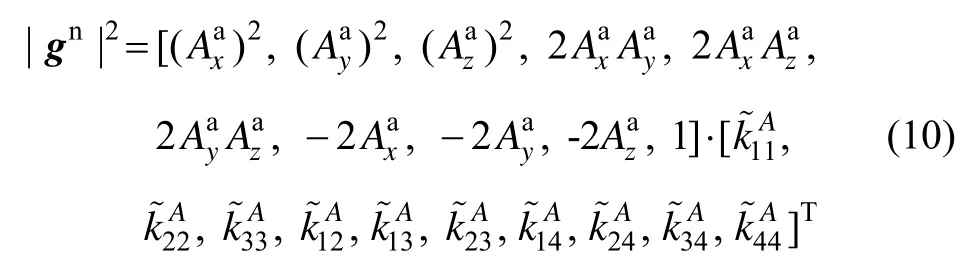
由于加速度通道存在9个待求参数，根据上述关系，将IMU静态放置于大于等于9个非共面的不同位置采集加计输出数据，即可通过最小二乘的方法求解出中所有元素，进一步根据公式(9)中的对应关系求出加速度通道的系统参数 Ka和 Ba。

1.2.2 角速度通道粗标定

角速度通道的测量模型式(4)可进一步写成：

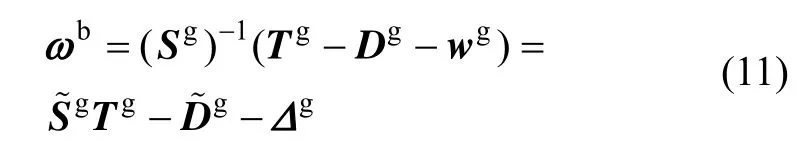
式中，

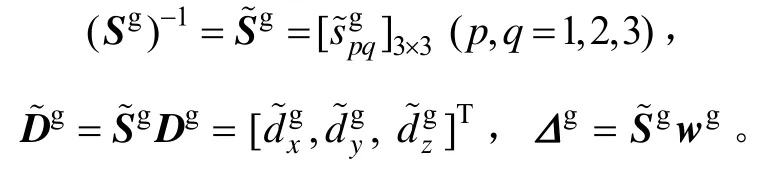
IMU静态情况下角速度通道输入与加速度通道输入的乘积存在以下关系：

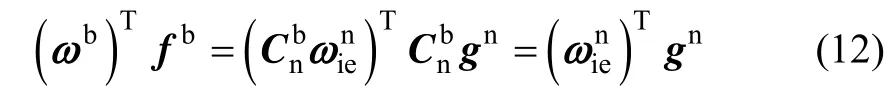
将式(11)带入式(12)中，得到：

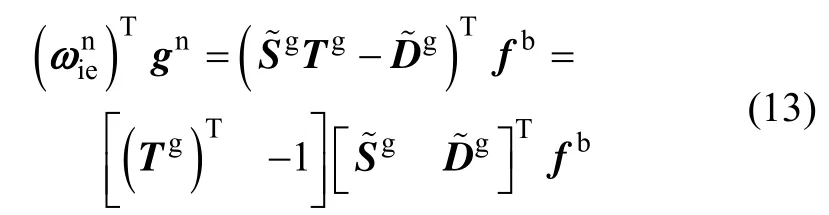
式中， fb可由式(6)计算。将式(13)展开为线性形式：

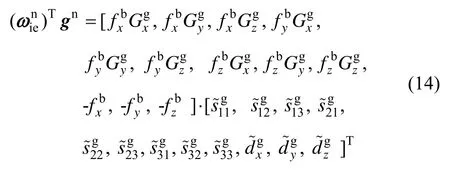
角速度通道存在12个待求系数，根据上述关系，只需将IMU静态放置于大于等于12个非共面不同位置采集陀螺和加计数据，即可通过最小二乘的方法求出及中对应元素，进一步根据矩阵运算得到角速度通道系统参数 Sg和 Dg。

由于地球自转角速度所提供的外部激励量值较小，上述方法角速度通道参数的精度较低。因此，需要设计相应的kalman滤波器对系统参数进行修正。

2 基于Kalman滤波的IMU系统参数修正

2.1 IMU测量误差模型

考虑到粗标定得到系统参数的不准确性以及传感器随机噪声的影响，由式(1)可推出 IMU加速度通道的测量误差模型为：

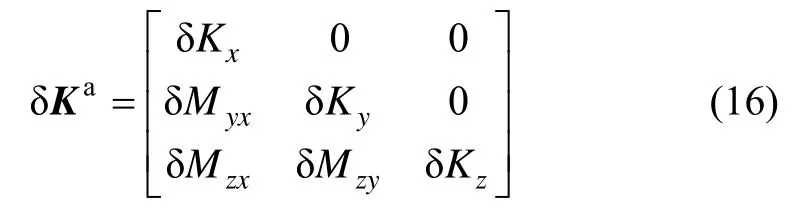
式中，δKi(i = x,y,z)为粗标定加计标度因数的残差，δMij(i = y,z; j = x,y;i ≠ j )为粗标定加计安装系数的残差。同理，由式(4)可推出 IMU角速度通道测量误差模型：

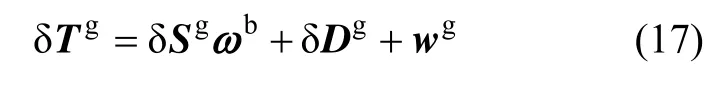
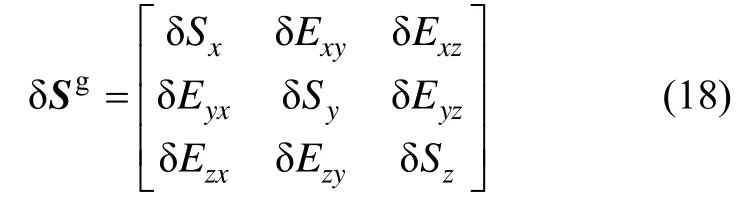
式中，δSi(i = x,y,z)为粗标定陀螺标度因数的残差，δEij(i, j = x,y,z;i ≠ j )为粗标定陀螺安装系数残差。

2.2 Kalman滤波状态方程

基于传统的INS/GPS组合滤波以及INS空中机动对准技术[12-14]，本文选取转台运动过程中IMU的速度误差、姿态误差以及上述系统参数残差 δBa、 δKa、δDg和 δSg构成滤波状态向量。具体如下所示：

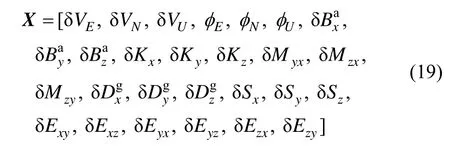
式中，δVE、δVN和δVU表示IMU捷联解算过程中导航坐标系下东向、北向和天向的速度误差，φE、φN和φU表示俯仰、横滚和航向角误差。

在推导滤波状态方程之前，首先需要将加速度计的测量误差从a系转换到n系中，即：

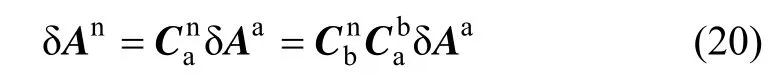
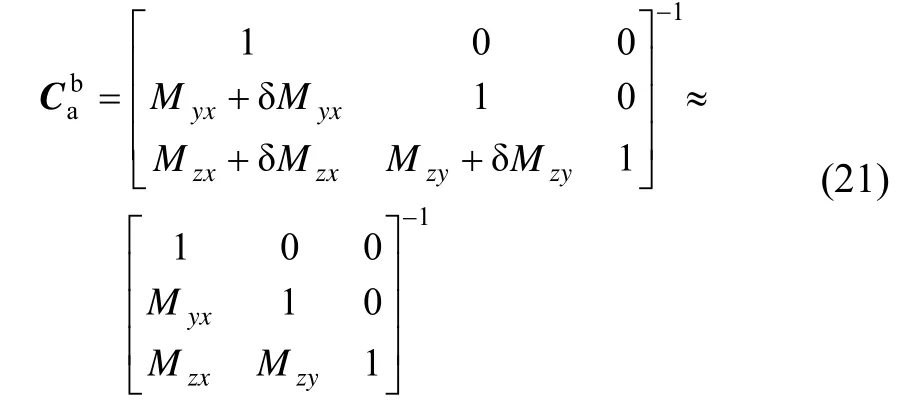
将公式(20)展开得到：

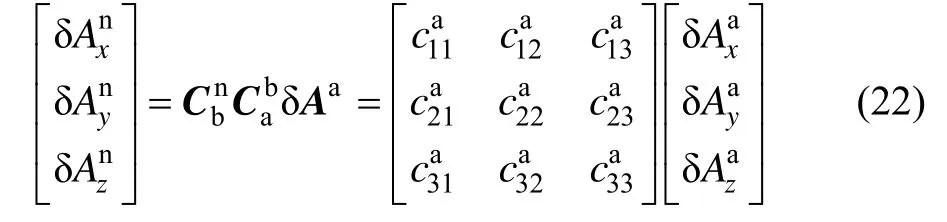
同理，将陀螺仪的测量误差从g系转换到n系下，可得到下式：

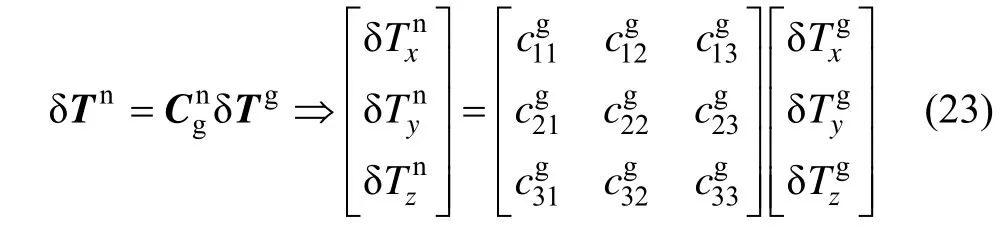
将 n系下陀螺和加计的测量误差式(22)和(23)扩充到惯导系统误差方程中，得到标定状态下滤波方程：

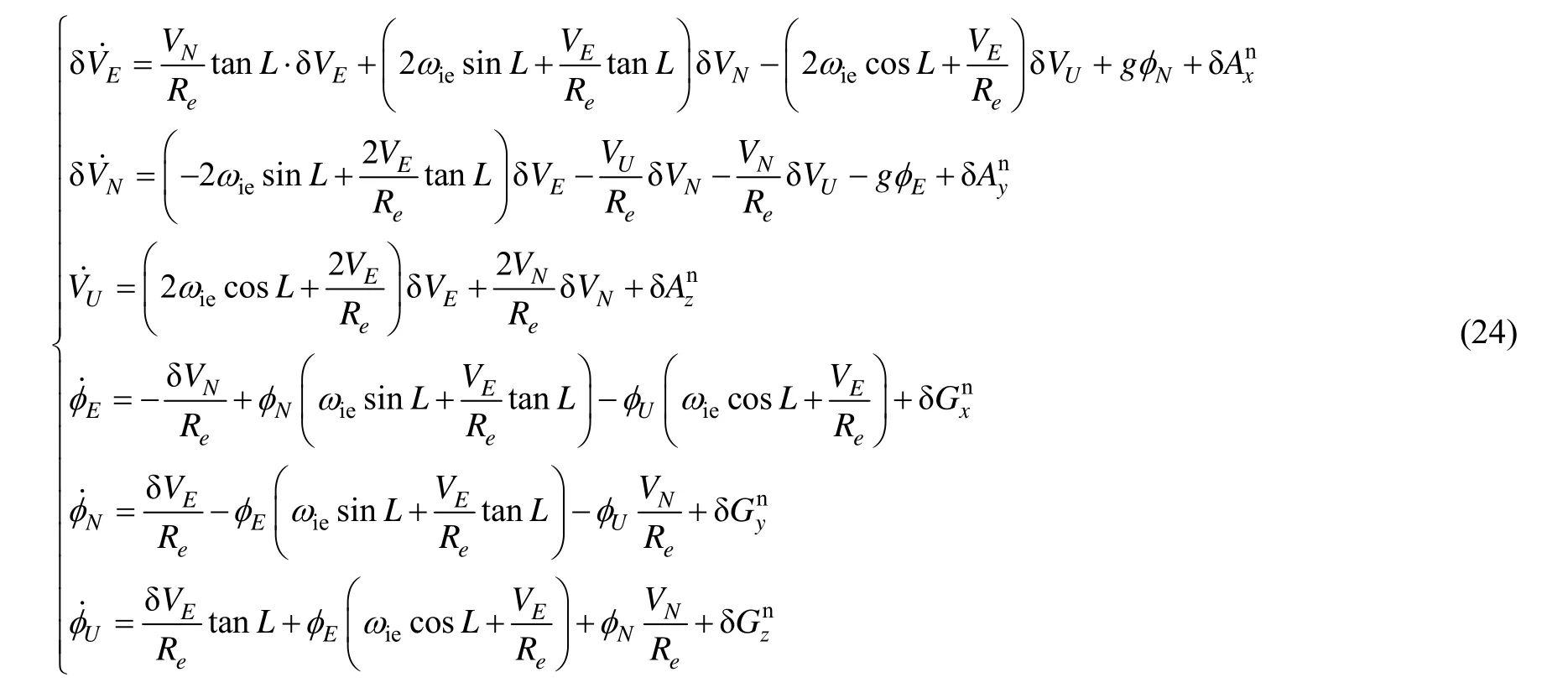
式中， Re为地球半径，L是当地纬度， VE、 VN和 VU分别表示捷联解算的东向、北向及天向速度。滤波状态方程可进一步写成：

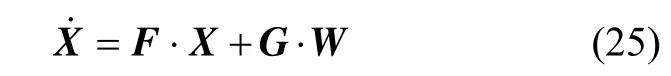
式中，X为式(19)所示27维系统状态向量，F为27 ×27维系统状态转移矩阵，G为27×6维系统噪声转移矩阵；W是6维系统噪声向量，表示为：

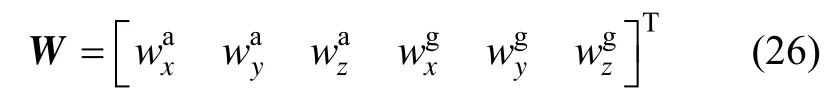
系统噪声转移矩阵G可表示为：

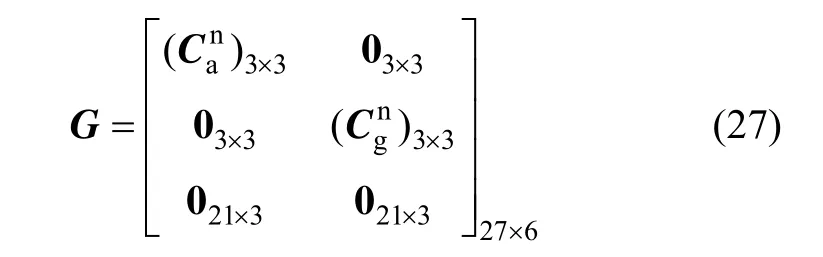
系统状态转移矩阵F可表示为：

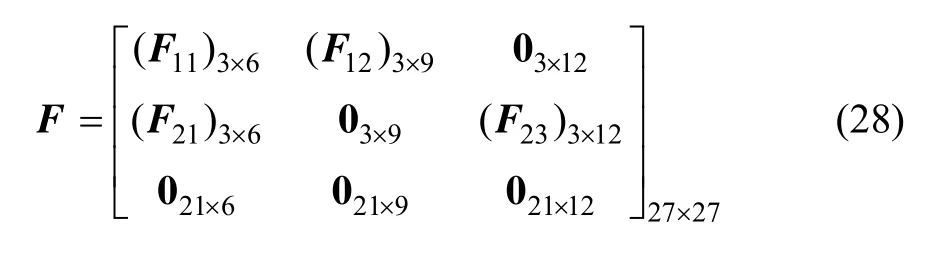
其中对应元素表示如下：

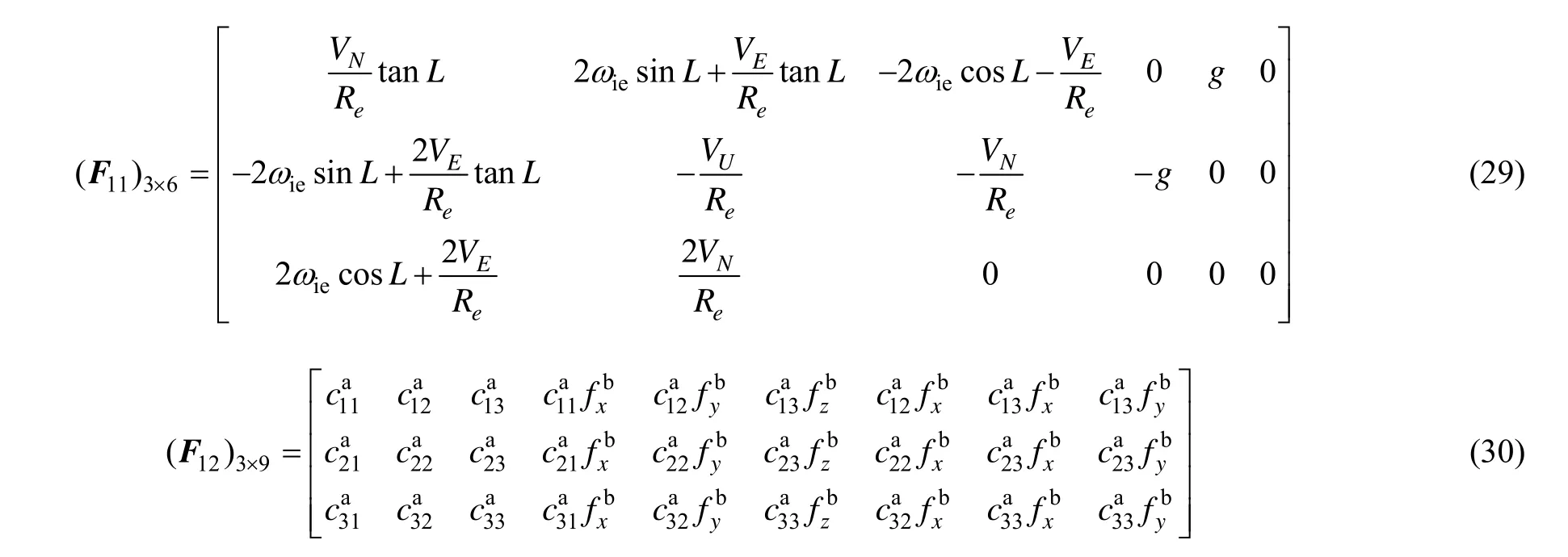
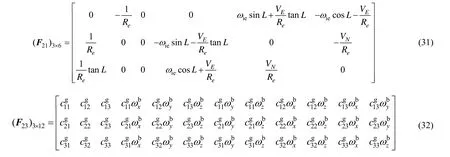
2.3 Kalman滤波量测方程

IMU随转台运动进行标定，只存在角运动，没有线运动，但由于系统参数误差，以及加计敏感中心与转台转轴不重合引起IMU内杆臂速度误差，使得IMU导航解算过程产生了非零线速度。因而，将经内杆臂速度误差补偿后的IMU速度误差作为滤波的观测量。

假设 IMU中三个方向加速度计测量敏感轴与转台对应转轴之间距离构成的内杆臂向量为：

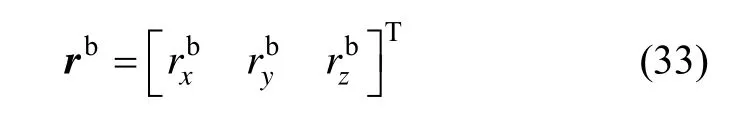
那么由于内杆臂效应而产生的速度误差在 IMU导航坐标系下可以表示为：

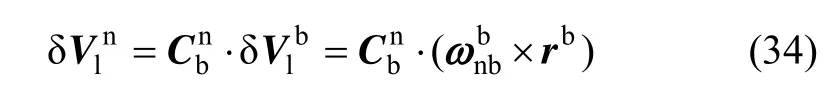
经内杆臂速度误差补偿后的 IMU惯性导航速度误差可以表示为：

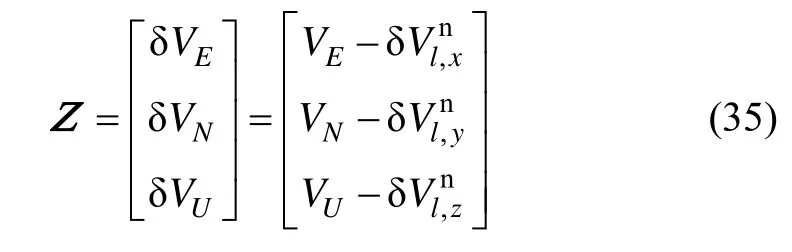
定义以IMU速度误差为观测量的滤波量测方程：

式中， H=[diag｛1, 1, 1｝ 03×24]为量测矩阵，v=[vx, vy, vz]T为量测噪声。

2.4 标定路径设计

转台带动IMU运动进行标定过程中，需要设计有效转动路径，使得因系统参数误差引起的IMU导航速度误差被有效的激励出来，如标定加速度计相关参数误差需要将其置于重力加速度输入的静态环境下，标定陀螺仪相关参数误差需要将其置于较大角速度（如5～10 (°)/s）输入的转动环境下，由此保证标定精度。

2.5 IMU系统参数的确定

利用 Kalman滤波估计得到的系统参数残差对粗标定结果进行修正，可得到激光陀螺IMU系统参数的高精度标定结果，表示为：

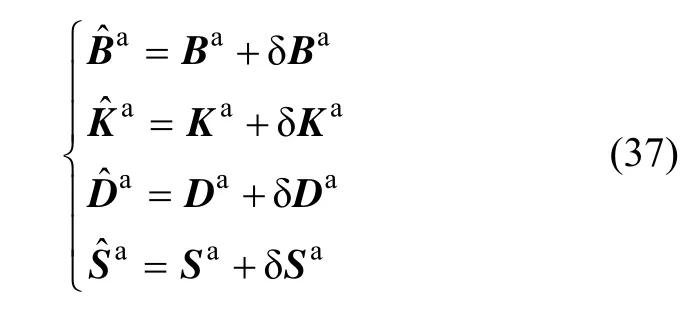
3 实验及分析

3.1 激光陀螺IMU系统组成

本实验室研制的高精度激光陀螺IMU如图1所示。由三支精度为0.01(°)/h的激光陀螺仪、三支精度优于10 μg的石英挠性加速度计、配套电路以及相应的机械结构组成。其体积为 200 mm×190 mm×112 mm，重量优于5.3 kg。该系统已被应用于位置姿态测量系统中。

图1 激光陀螺IMUFig.1 RLG inertial measurement unit

3.2 标定实验及结果

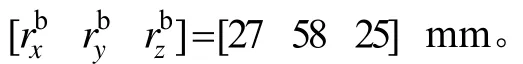
图2 激光陀螺IMU标定Fig.2 Calibration of RLG IMU

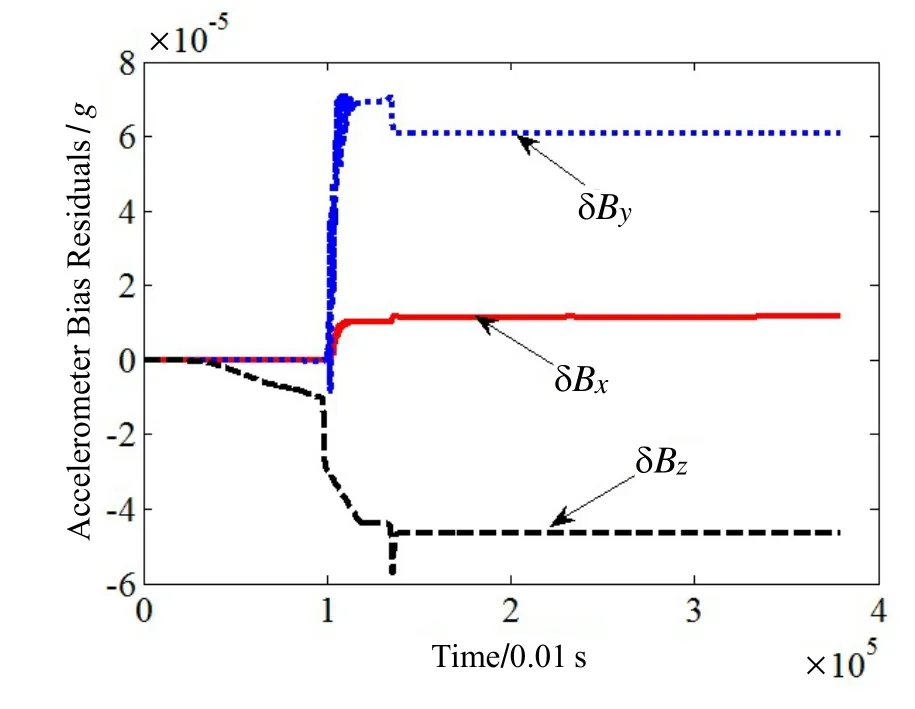
图3 加速度计偏置残差估计结果Fig.3 Estimated residuals of accelerometers bias

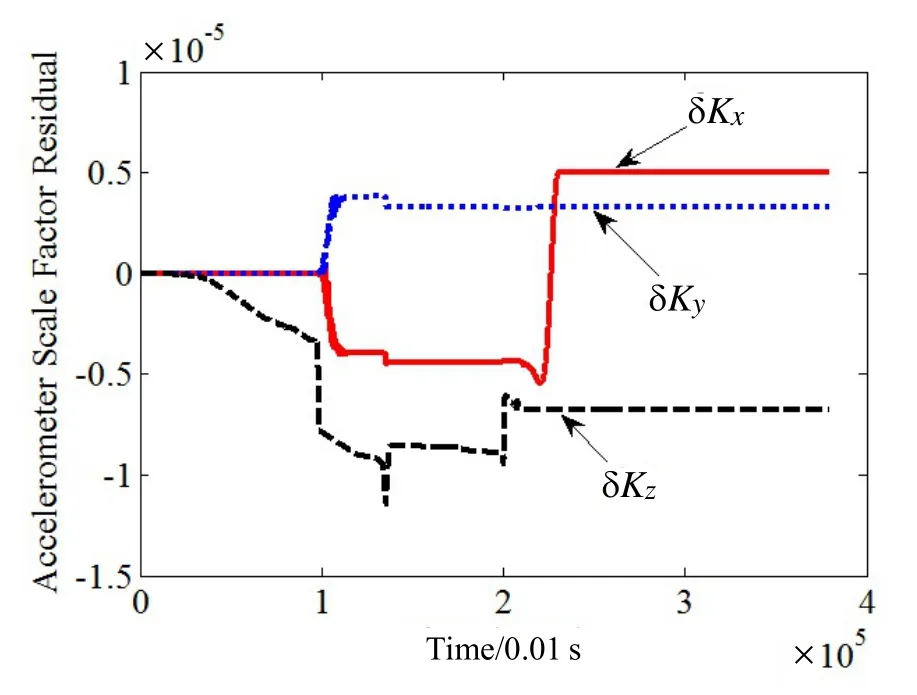
图4 加速度计标度因数残差估计结果Fig.4 Estimated residuals of accelerometers scale factor

系统参数粗标定结果如表1中第二列所示，通过Kalman滤波估计的残差结果如表1中第三列所示，各系数的估计曲线如图3～8所示。可见，各系数残差均已收敛。利用滤波估计得到的系数残差对粗标定结果进行修正，得到最终的IMU系统参数的高精度标定结果如表1中第四列所示。

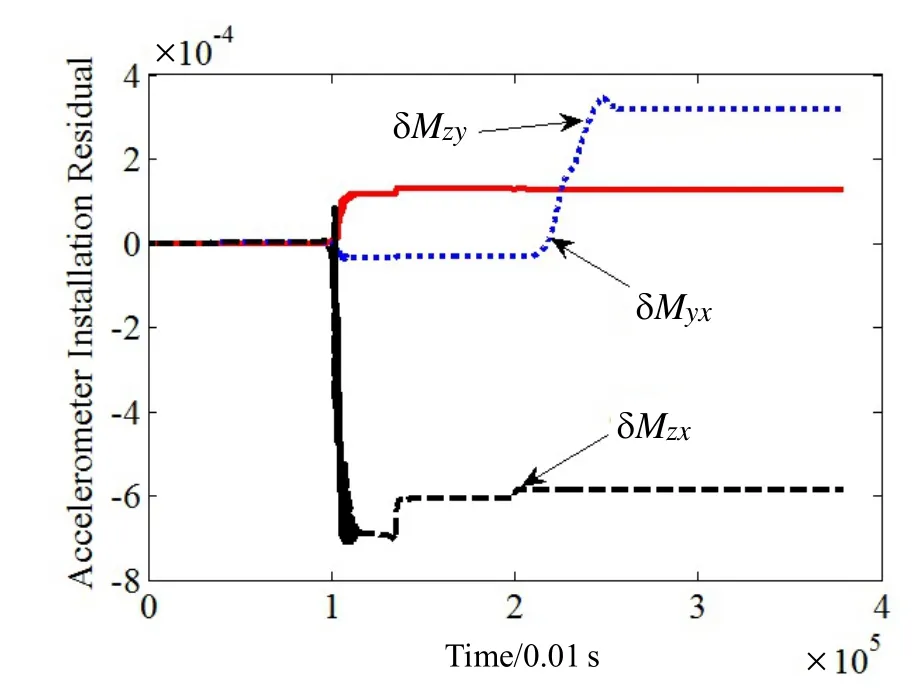
图5 加速度计安装系数残差估计结果Fig.5 Estimated residuals of accelerometers installation

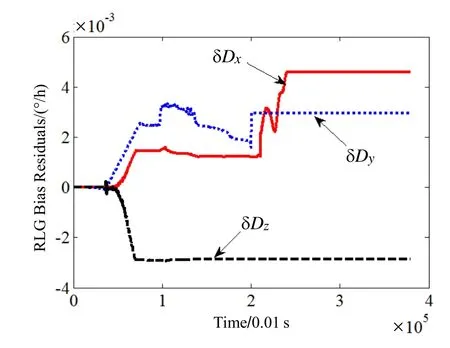
图6 激光陀螺零偏残差估计结果Fig.6 Estimated residuals of RLG bias

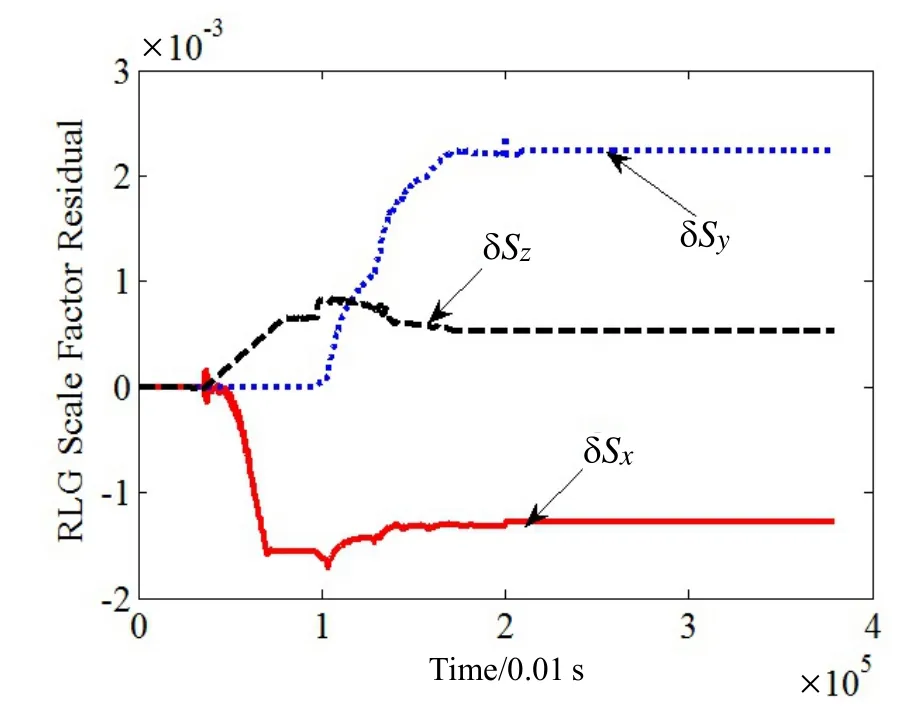
图7 激光陀螺标度因数残差估计结果Fig.7 Estimated residuals of RLG scale factor

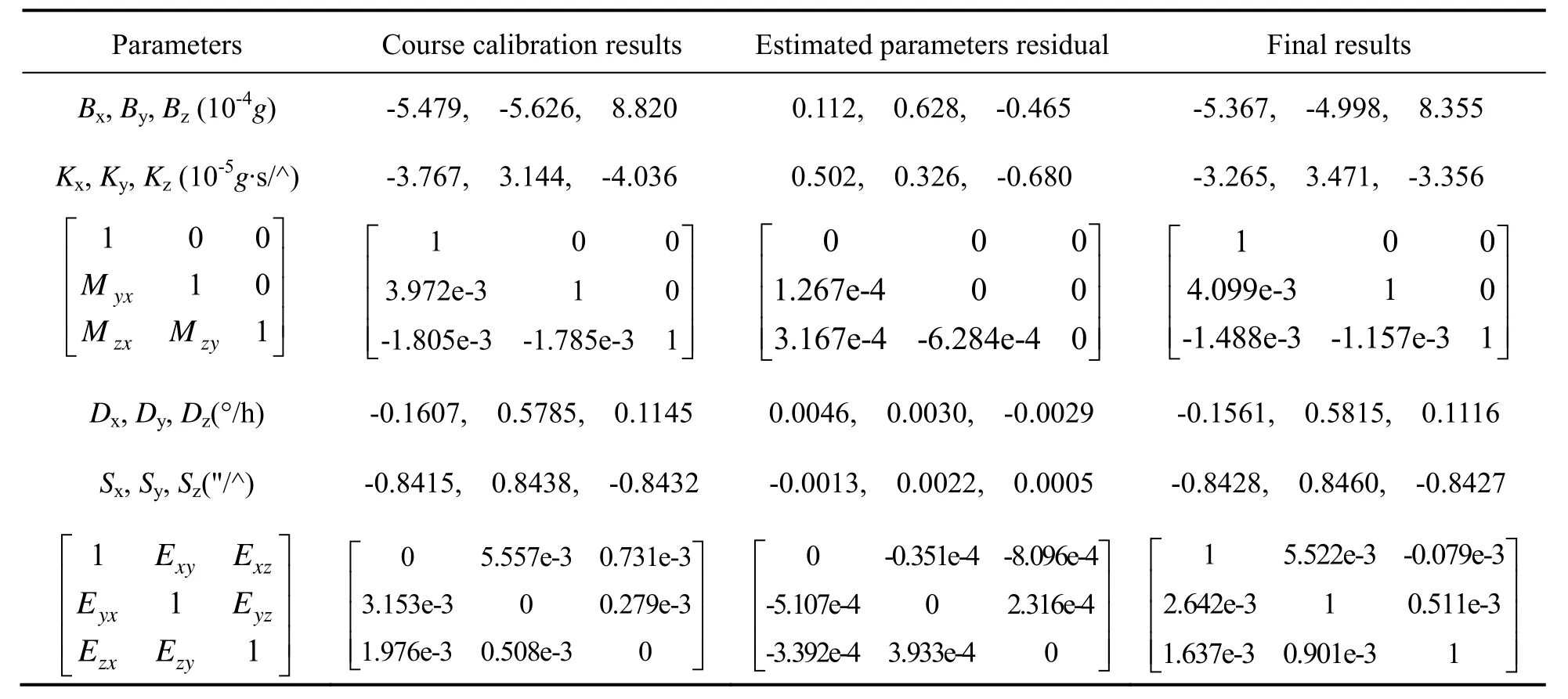
表 1 IMU系统参数标定结果Tab.1 Calibrated parameters of IMU

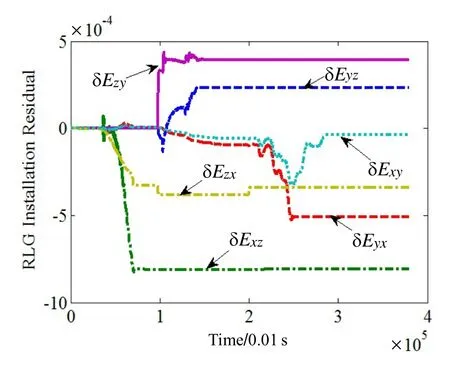
图8 激光陀螺安装系数残差估计结果Fig.8 Estimated residuals of RLG installation

3.3 车载验证实验及结果

为了验证利用本文方法得到的标定系数的准确性，对标定的激光陀螺IMU进行跑车实验，考察其纯惯性导航精度，同时与文献[4]中传统动静结合的标定方法（采用高精度三轴转台，位置精度0.001°，转动速率精度为0.001 (°)/s）得到的系统参数的导航结果进行对比。跑车实验的路线为北京市五环路，利用GPS的位置数据作为真实值进行位置误差检校。

实验过程中，首先启动IMU预热30 min，然后行驶至起点处使车辆静止300 s进行初始对准，再以60公里/小时的速度行驶1 h后停止，计算停止点纯惯性导航的位置误差。实验共进行7组，对应两种标定方法的导航位置误差如表2所示，其中第1组实验的位置轨迹如图9所示。从表2可以看出，本文提出方法得到系统参数对应的纯惯性导航位置精度与传统方法相当，均达到优于0.6 n mile/h的水平，满足高精度激光陀螺IMU的使用需求。

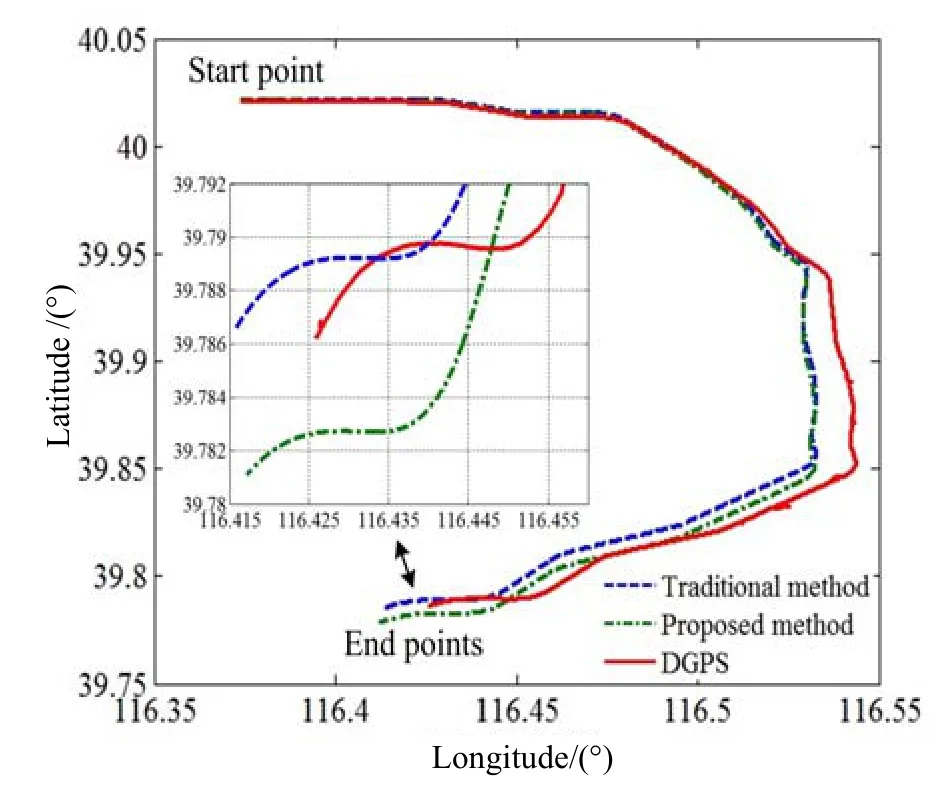
图9 第1组车载实验轨迹Fig.9 Trajectories of the first group vehicle experiment

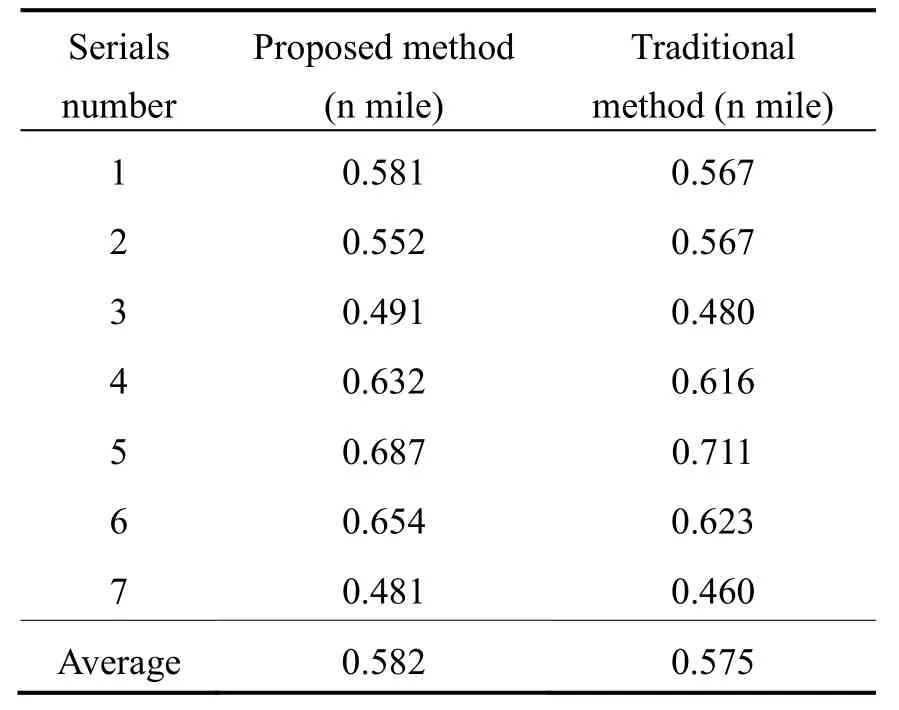
表 2 1 h车载实验位置误差Tab.2 Position errors of 1 h vehicle experiments

4 结 论

采用传统的动静结合的方法标定惯性测量单元，其缺点在于标定精度严重依赖于所使用转台的精度。因此，高精度激光陀螺IMU通常需要使用价格昂贵的高精度精密转台才能标定，大大增加了IMU的生产成本。

针对上述问题，本文提出一种完全不依赖转台精度的静态解析标定与 Kalman滤波估计混合的新型高精度标定方法。首先采用多位置静态解析标定方法，以地球自转角速度和重力加速度为激励粗标定出IMU系统参数的低精度初始值；然后基于惯导误差方程，建立以IMU系统参数粗标定结果的标定残差为状态变量，以经过内杆臂补偿后的导航速度误差为观测量的扩展 Kalman滤波器，估计出系统参数残差；再利用残差对初始值进行修正，得到IMU系统参数的高精度标定结果。

车载实验结果表明，本文方法获得的标定结果与依赖高精度转台的传统方法相当，满足高精度激光陀螺IMU的使用需求。

（References）：

[1] Titterton D H, Weston J L. Strapdown inertial navigation technology[M]. 2nd Ed. Lexington: American Institute of Aeronautics and Astronautics, 2004.

[2] Li J, Fang J, Ge S. Kinetics and design of a mechanically dithered ring laser gyroscope position and orientation system[J]. IEEE Transactions on Instrumentation and Measurement, 2013, 62: 210-220.

[3] 谢波，秦永元，万彦辉. 激光陀螺捷联惯导系统多位置标定方法[J]. 中国惯性技术学报，2011，19(2)：157-169.

XIE Bo, QIN Yong-yuan, WAN Yan-hui. Multiposition calibration method of laser gyro SINS[J]. Journal of Chinese Inertial Technology, 2011, 19(2): 157-169.

[4] 陈北欧，孙文胜，张桂宏，等. 捷联组合(设备无定向)六位置测试标定[J]. 导弹与航天运载技术，2001，3(3)：23-27.

CHEN Bei-ou, SUN Wen-sheng, ZHANG Gui-hong, et al.. Strapdown unit(without orientation) six-position test calibration [J]. Missile and Space Vehicle, 2001, 3(3): 23-27.

[5] 刘百奇，房建成. 一种改进的IMU无定向动静混合高精度标定方法[J]. 仪器仪表学报，2008，29(6)：1250-1254.

LIU Bai-qi, FANG Jian-cheng. Modified hybrid calibration method for IMU without orientation[J]. Chinese Journal of Scientific Instrument, 2008, 29(6): 1250-1254.

[6] 周章华，吴亮华，张伟，练涛. 捷联惯导系统在非转台条件下的全参数标定[J]. 中国惯性技术学报，2013，21(5)：570-575，579.

ZHOU Zhang-hua, WU Liang-hua, ZHANG Wei, LIAN Tao. Full parameters calibration for SINS without turntable[J]. Journal of Chinese Inertial Technology, 2013, 21(5): 570-575, 579.

[7] Syed Z F, Aggarwal P, Goodall C et al.. A new multi-position calibration method for MEMS inertial navigation systems[J]. Measurement Science and Technology, 2007, 18: 1897-1907.

[8] Zhang Hongliang, Wu Yuanxin, Wu Wenqi, et al., Improved multi-position calibration for inertial measurement units[J]. Measurement Science and Technology, 2010, 21: 015107.

[9] Mohinder S.G, Vinson D. H and Randy S. M. Application of kalman filtering to the calibration and alignment of inertial navigation system[J]. IEEE Transactions on Automatic Control, 1991, 36(1): 4-13.

[10] 吴赛成，秦石乔，王省书，等. 激光陀螺惯性测量单元系统级标定方法[J]. 中国惯性技术学报，2011，19(2)：185-189.

WU Sai-cheng, QIN Shi-qiao, WANG Xing-shu, et al. Systematic calibration method for RLG inertial measurement unit[J]. Journal of Chinese Inertial Technology, 2011, 19 (2): 185-189.

[11] 张小跃，张春熹，宋凝芳. 基于组合导航技术的光纤捷联系统在线标定[J]. 航空学报，2008，29(6)：1656-1659.

ZHANG Xiao-yue, ZHANG Chun-xi, SONG Ning-fang. Online calibration of FOG strapdown system based on integrated navigation technology[J]. Acta Aeronautica et Astronaut Ica Sinica, 2008, 29(6): 1656-1659.

[12] Fang Jiancheng, Yang Sheng. Study on innovation adaptive EKF for in-flight alignment of airborne POS[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(4): 1378-1388.

[13] Fang Jiancheng, Gong Xiaolin. Predictive iterated kalman filter for INS/GPS integration and its application to SAR motion compensation[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(4): 909-915.

[14] 刘锡祥，徐晓苏. 惯性测量组件整体标定技术[J]. 中国惯性技术学报，2009，17(5)：568-576.

Liu Xixiang, Xu Xiaosu. System calibration techniques for inertial measurement units[J]. Journal of Chinese Inertial Technology, 2009, 17(5): 568-576.

Integrated calibration method for RLG IMU

CHENG Jun-chao, FANG Jian-cheng, WU Wei-ren, LI Jian-li, WANG Wen-jian
(Science & Technology on Inertial Laboratory, Key Laboratory of Fundamental Science for National Defense-Novel Inertial Instrument & Navigation System Technology, Beihang University, Beijing 100191, China)

To solve the problem in using low-accuracy turntable to calibrate the high-precision ring laser gyroscope inertial measurement unit, a new integrated calibration method is proposed. At first, a static analytical calibration method is applied to coarsely calibrate the initial values of IMU system parameters. Then, based on the error function of strapdown inertial navigation algorithm, an extended Kalman filter is established to refine the obtained coarse parameters. The experiment results show that, the proposed method is able to acquire high-precision calibrated results by using low-accuracy turntable, which decreases the calibration cost of IMU and satisfies the precision requirement of RLG IMU.

ring laser gyroscope; inertial measurement unit; integrated calibration; error compensation; kalman filter

联 系 人：房建成（1965—），男，教授，博士生导师。E-mail：fangjiancheng@buaa.edu.cn

1005-6734(2014)04-0445-04

10.13695/j.cnki.12-1222/o3.2014.04.005

U666.12

A

2014-01-14；

2014-04-17

国家973重大基础研究项目资助（2009CB724002）；国家自然科学基金（60825305, 61121003, 61104198）

程骏超（1983—），男，博士研究生，从事组合导航研究。E-mail：junchaocheng@163.com