碳掺杂α-S8的光学性质和弹性性质的第一性原理计算

阮林伟 朱玉俊,* 裘灵光,* 卢运祥

(1安徽大学化学化工学院,合肥 230601;2华东理工大学化学系,上海 200237）

1 引言

由于21世纪能源短缺和环境污染的问题日益严重,寻找新能源以及治理环境污染的技术已经变得迫在眉睫.由于光催化剂能将太阳能转化为化学能且能分解污染物,因而成为当前研究的热点.1-5理想的光催化剂应该具有催化活性高、稳定性能好、合成简单、无污染、原料便宜易得等优点.自1972年Fujishima和Honda6发现TiO2光催化剂之后,其他各种光催化剂如BiVO4、7Bi2WO6、8,9Ag2CrO4、10BiPO411等相继被发现,但这些光催化剂并不能很好地满足以上的标准.虽然TiO2的催化效率高、稳定性能好、价格低廉,但是由于它的带隙太宽以至于不能有效地吸收可见光,12从而限制了材料的光催化活性,而其他的传统光催化剂大多由于含有重金属离子不仅价格昂贵而且还会造成环境污染,所以寻找一种条件适宜的光催化剂是目前实验和理论研究的重要方向.

S元素有多种同素异形体,能够形成各种不同的环状结构,其中以八元环的结构最为稳定,而八元环的S8结构在标准条件下又有3种不同的构型,分别是:正交晶系的α-S8、单斜晶系的β-S8和γ-S8,其中又以正交晶系的α-S8最为稳定.最近,Liu等13发现α-S8可作为一种高效的元素光催化剂用于光解水和降解有机物,并且作为一种非金属光催化剂,α-S8不会造成环境污染且原料简单、合成方便,预示着其在光催化领域具有巨大的应用潜力.但是实验发现受制于催化剂的大尺寸、弱的亲水性以及较短的光吸收波长,α-S8仍然表现出低的光催化活性,在Liu等13的工作中,作者预测可以通过表面改性、纳米尺度、掺杂以及与其他光催化剂耦合的方法来弥补这些缺点,从而改善它的光催化性能.受此启发,Wang等14通过实验的方法合成了异质结构Graphene-g-C3N4-α-S8,结果表明新合成的物质光催化性能与α-S8相比得到了极大的提高,表明Liu等的设想具有一定的实验可行性.掺杂是在一种材料中掺入少量其它元素或化合物,以使材料性质和性能发生相应的改变,从而具有实际应用价值或特定用途的过程,近年来已有大量实验证明掺杂能改变材料的电子结构、表面性质从而提高材料的性能.15-20当前已报道的非金属光催化剂只有g-C3N4和α-S8,其中对于g-C3N4的实验和理论研究已趋于完备却很少有关于α-S8的理论探索.本文即是基于第一性原理密度泛函的方法首次通过在α-S8中掺杂C原子来探索掺杂后材料电子结构、能带结构、光学性质、弹性性质以及各向异性的变化规律,从而为以后的实验研究提供理论的指导.

2 计算方法

本文采用密度泛函理论平面波赝势法进行计算,采用局域密度近似(LDA）中CA-PZ泛函21处理相关势能.赝势设置为ultrasoft赝势,22赝势表示方法为倒易空间.平面波截断能(Ecut=280 eV）与Liu等13的报道相一致,系统总能量和电荷密度在布里渊区的积分计算使用Monkhorst-Pack方案23来选择k网格点为5×5×5,收敛性测试表明截断能和k点的选择能保证结构在完备平面波基水平上收敛.在自洽场计算中,采用Pulay密度混合法,每个原子自洽场设为5.0×10-7eV·atom-1,在对模型结构进行优化中采用BFGS算法.24在对晶体进行结构优化和单点能计算的过程中,保证能量收敛标准为5.0×10-6eV·atom-1,原子间相互作用力低于0.1 eV·nm-1,最大应力低于0.02 GPa,原子最大位移不超过5.0×10-5nm.在弹性常数的计算过程中,每个应变模式设置为6步,最大应变振幅设为0.005,能量收敛标准设为4.0×10-6eV·atom-1,原子间相互作用力低于0.1 eV·nm-1,原子最大位移不超过4.0×10-5nm.本文利用CASTEP模块25进行计算,原子赝势计算选取的价电子分别为C 2s22p2、S 3s23p4.

3 结果与讨论

3.1 电子结构

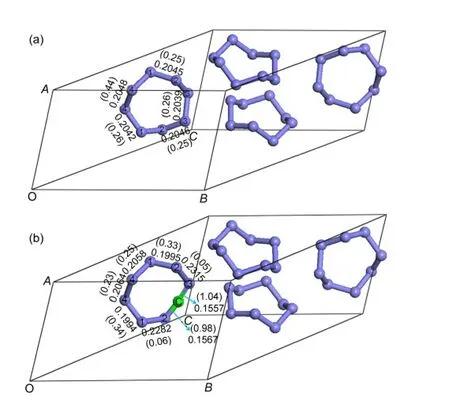
图1 纯α-S8(a）及碳掺杂α-S8(b）的结构Fig.1 Structures of pure(a）and carbon-doped(b）α-S8Bond length(nm）and corresponding bond overlap population(data in bracket）.

由图1(a）可以看到,α-S8晶体的每个原胞包括4个独立的八元环,每个环由8个硫原子以单键相连而成,而环与环之间无任何化学键连接.α-S8晶体的八元环上有4种不同的对称性硫原子,在图1(a）中,分别用1、2、3、4表示.由图可知,纯α-S8结构中存在5种不同的 S―S 键,即 S1―S2、S1―S4、S2―S3、S3―S3和S4―S4键.计算结果显示,不同S―S键的键长相差很小,重叠布居数非常接近,且都为正值,Mulliken电荷都为0,说明α-S8晶体中硫原子之间以强的共价键相连,无电荷转移.由于每个α-S8原胞中有32个S原子,我们采取在每个原胞中掺杂一个C原子,即掺杂的原子浓度为3.125%,以此来探索C原子在α-S8中掺杂后对晶体电子结构、光学性质、弹性性质以及各向异性的影响.

首先,为了得到C原子在α-S8中的最佳掺杂位,分别计算了掺杂后体系的形成能,即反应初始态与终态的能量之差,包括C原子在S位的4种取代掺杂体系和C原子在α-S8中的间隙掺杂体系.本文形成能的计算基于以下公式:26

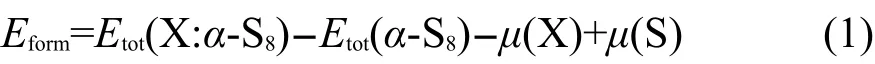
其中,Etot(X:α-S8）为掺杂后体系的总能量;Etot(α-S8）为掺杂前体系的总能量;μ(X）为掺杂原子的化学势;μ(S）为被取代S原子的化学势.在本文中,S原子和C原子的化学势可分别由纯α-S8分子以及固体石墨得到,即:μ(S）=μ(α-S8）/32,μ(C）=μ(graphite）/4.值得注意的是,在本文式(1）中的X表示C原子,在计算间隙掺杂形成能时,因为S原子未被C原子取代,所以μ(S）一项应省去.计算得到C在S1、S2、S3、S4位上的取代掺杂形成能分别为2.3061、2.3351、2.3034、2.3040 eV,间隙掺杂形成能为3.8691 eV.形成能越小说明掺杂反应越容易进行,相应的杂质缺陷也越容易形成,当形成能为负值时,表明反应能自发进行.由计算结果可知,首先,C原子在S位上的取代掺杂和在α-S8晶体中的间隙掺杂形成能都为正值,表明掺杂需要吸收能量,取代反应相对进行困难.其次,C原子在S位上的取代掺杂形成能明显低于C原子在α-S8晶体中的间隙掺杂形成能,说明C原子在α-S8中的取代掺杂更易于进行.最后,我们发现C原子在不同S位的取代掺杂形成能相差非常小,但是在S3位的取代掺杂形成能最低,表明虽然C原子在不同S位上的取代几率相近,但是C原子应该在S3位最容易发生取代.在以下的计算和分析过程中我们取C原子取代S3位S原子形成的结构为分析对象.

表1所示为α-S8掺杂前后晶体结构参数的变化.由表1可以看出,纯α-S8晶体经LDA(CA-PZ）泛函优化后,得到a=0.7898 nm,c=1.3244 nm,而b=1.2748 nm略小于Liu等13的实验结果(1.2866 nm）.纯α-S8的密度为2.3783 g·cm-3,与非金属共价化合物g-C3N4的密度非常接近,27说明虽然S原子的相对原子质量大于C和N,但是由于α-S8晶体中存在非常大的空隙空间导致了α-S8的晶体密度下降.掺杂后,晶格常数a和b以及角度α和β都降低,但是c和γ却明显地增大,说明C原子在α-S8晶体中掺杂后,晶体中分子间相互作用力在O A和O B方向增强了,而在O C方向却得到了削弱.此外,掺杂后晶体的体积和密度也减小了,虽然C原子取代S原子后导致了晶体质量的下降,但是由于其下降的幅度大于晶胞体积的下降幅度,所以导致了晶体的密度降低.

在图1(a）中,我们展示了纯α-S8结构中不同S―S键的键长和键重叠布居数,在图1(b）中,显示了C掺杂α-S8晶体后不同的S―S键的键长和键重叠布居数变化以及新形成的C―S键的键长和键重叠布居数.从图中可以看出,新形成的C―S2和C―S3键的键长分别为0.1567和0.1557 nm,都小于取代前的S2―S3与S3―S3的键长,而其键重叠布居数分别为0.98、1.04,与掺杂前的键重叠布居数相比,增加了0.73和0.78.我们还发现与C―S2和C―S3键相连的S1―S2与S2―S3键的键长与掺杂前相比变长了,而键重叠布居数却降低至接近于0,而其他的S―S键的键长和键重叠布居数却变化很小,计算结果显示Mulliken电荷从S原子转移到C原子约为0.56e.所有这些变化都说明C掺杂α-S8后形成的C―S键的共价性强于掺杂前的S―S键.从计算结果还可得到,纯α-S8中S原子核外电子的轨道布居为3s1.883p4.12,C掺杂α-S8后,取代C原子的核外电子的轨道布居为2s1.202p3.38.C掺杂α-S8后,C原子的p轨道与S环中其他的S原子的p轨道发生了部分重叠,导致了本文中的碳硫键比芳香环中的C―S和一般的C＝S都要缩短.纯α-S8与掺杂后结构的电荷密度如图2所示,图中的淡黄色区域代表S原子的电荷密度,红色区域表示C原子的电荷密度,可知红色区域的电荷密度明显强于淡黄色区域,也即C原子取代S原子之后会导致电荷密度明显增强.

表1 α-S8掺杂前后晶格常数以及密度(ρ）和体积(V）的变化Table 1 Change of lattice constants and density(ρ）and volume(V）of α-S8before and after doping

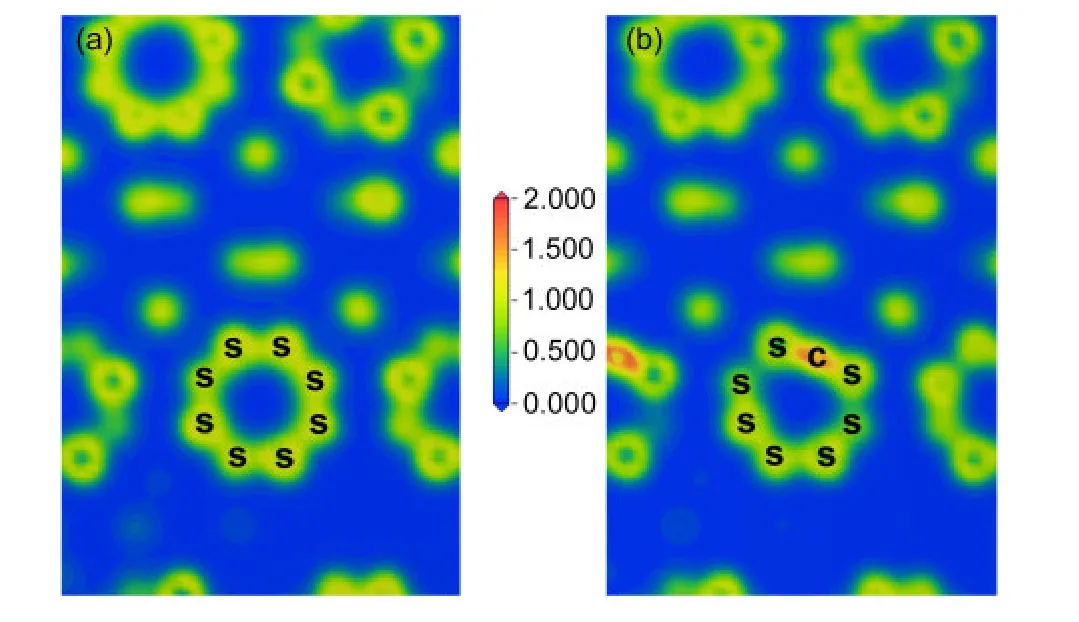
图2 纯α-S8(a）与碳掺杂α-S8(b）的电荷密度图Fig.2 Charge densities of pure α-S8(a）and carbon-doped α-S8(b）

3.2 能带结构和态密度

图3为纯α-S8与掺杂α-S8的能带图,纯α-S8的带隙宽度为1.69 eV,小于实验值(2.79 eV）13.我们知道密度泛函理论-局域密度近似(DFT-LDA）在原子、分子和有机、无机固体的基态性质研究中获得巨大成功,但是处理半导体材料的电子结构中,存在带隙偏小问题,这已经被许多的实验结果所证实,28-31但是这并不影响本文对α-S8及其掺杂体系的变化规律的分析.由于纯α-S8与实验值相差1.10 eV,所以我们将1.10 eV作为本文能带、态密度以及光性质计算的修正值.如图3所示,修正后的纯α-S8以及掺杂α-S8的带隙值分别为2.79、2.64 eV.掺杂后的体系带隙值明显降低,表明掺杂体系的导电性能增强,催化效率得到了提高,同时也证明了在α-S8晶体中掺杂C原子是一种改善α-S8电子结构理论上可行的方法.由图3(a）还可以看到,纯α-S8的价带边缘在G-Y方向,而导带边缘在Z点,表明α-S8为间接带隙半导体,而在图3(b）中,掺杂结构的价带最高点和导带最高点都位于G点,表明C掺杂后的α-S8转化为直接带隙半导体.通过比较图3(a,b）,可以发现掺杂后的体系导带和价带都变得更加紧凑,表明掺杂后的体系原子杂化程度加强.

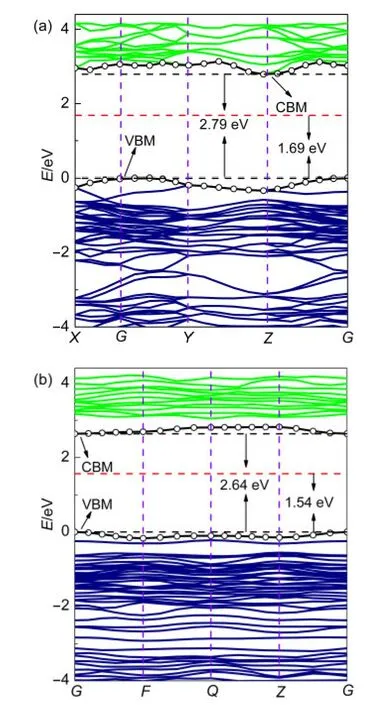
图3 纯α-S8(a）与碳掺杂α-S8(b）的能带图Fig.3 Band gaps of pure α-S8(a）and carbon-doped α-S8(b）

为了更好地描述C原子在α-S8晶体中掺杂后,电子轨道的贡献作用变化,分别计算了α-S8和掺杂结构的态密度(TDOS）以及单个原子的局部态密度(PDOS）,如图4所示.结果表明,费米能级处态密度为0,价带与导带之间的距离为2.79和2.64 eV,分别对应于纯α-S8和掺杂α-S8的带隙.α-S8的导带宽度为4.20 eV,主要是由S的3p轨道组成,α-S8价带的低能区(-17--7.5 eV）主要是由S的3s轨道组成,而S的3p轨道占据了α-S8的价带高能区(-7.5 eV到费米能级处）.图4(b）显示C原子在α-S8晶体中掺杂后,结构的价带的高能区和导带由S-3p与C-2p共同组成,由图可以看到二者发生了重叠,因此二者产生了高度杂化,这与图3中C原子掺杂α-S8后结构能带图的价带和导带都变得更加紧密相对应.

3.3 光学性质

了解固体物质的光学性质是非常重要的,特别是对于了解光催化剂α-S8在可见光照射下的光谱响应变化尤其显得不可或缺.在本文中我们计算了α-S8及其掺杂结构的介电函数曲线和光吸收曲线.据Saha等32所言,介电函数可以作为固体的其他光学性质的基础,即其他光学性质可以由介电函数推导得到.介电函数的虚部可以定义为:

图4 纯α-S8(a）与碳掺杂α-S8(b）的态密度(DOS）Fig.4 Density of states(DOS）of pure α-S8(a）and carbon-doped α-S8(b）

其中,V表示晶胞体积;e表示电子电荷;m为电子质量;ω表示光子频率;hω即为入射光子的能量;P为动量运算符;K n和K n′分别表示导带和价带波函数;K为晶体动量特征值;f(K n）为费米函数;E表示晶体能量.介电函数的实部ε1(ω）可根据Kramers-Kronig关系式33计算得到,定义如下:

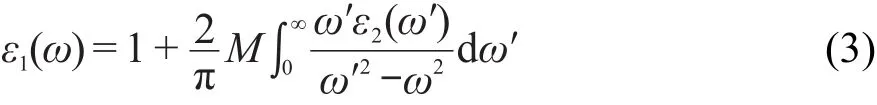
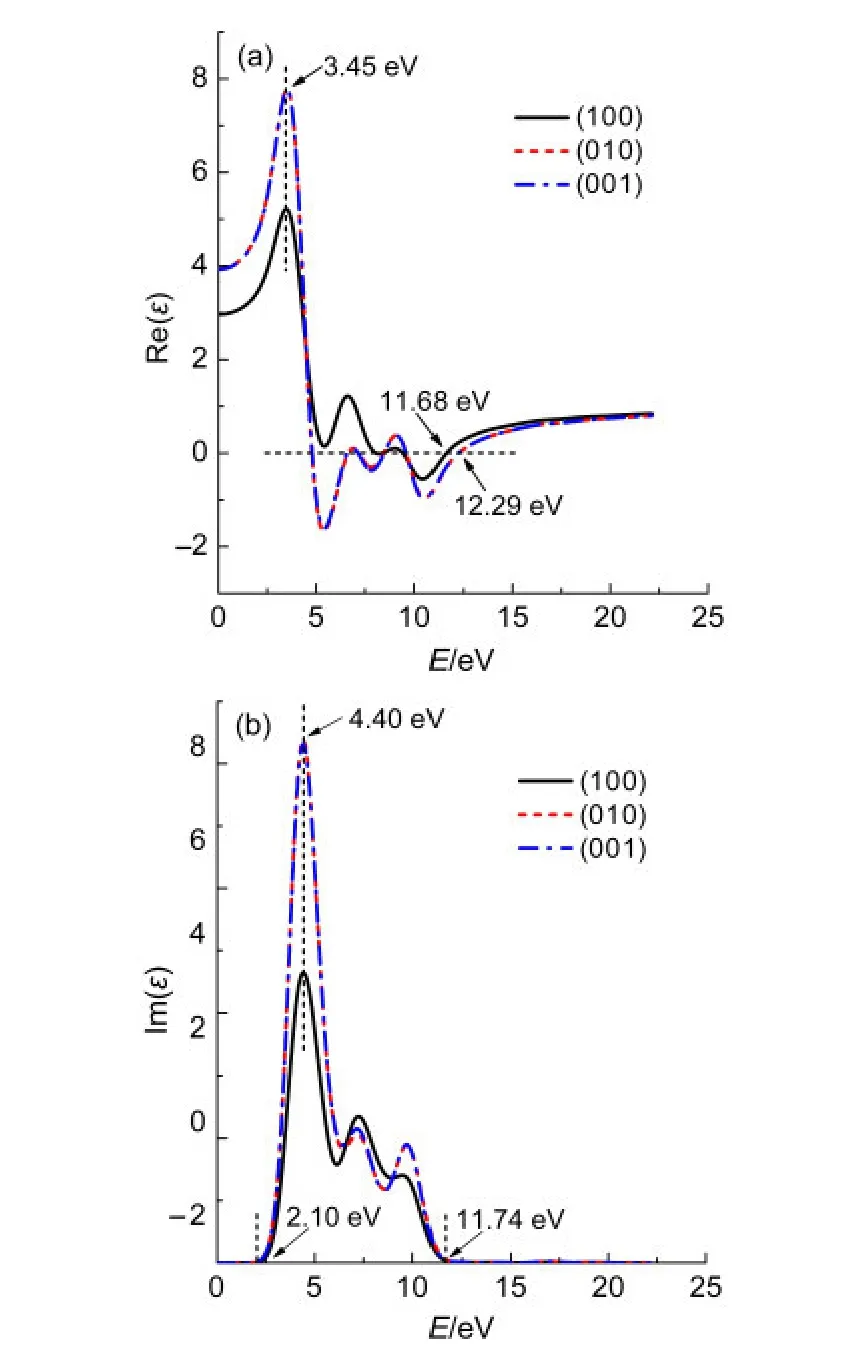
图5 纯α-S8介电函数在不同极化方向上的实部Re(ε）和虚部Im(ε）Fig.5 Real Re(ε）and imaginary Im(ε）parts of dielectric function for pure α-S8at different polarization directions

其中,M为积分的主值.根据定义的介电函数的虚部和实部,可以得到其他光学性质的计算公式,如光吸收系数I(ω）可表示为:32

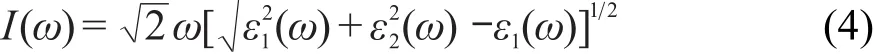
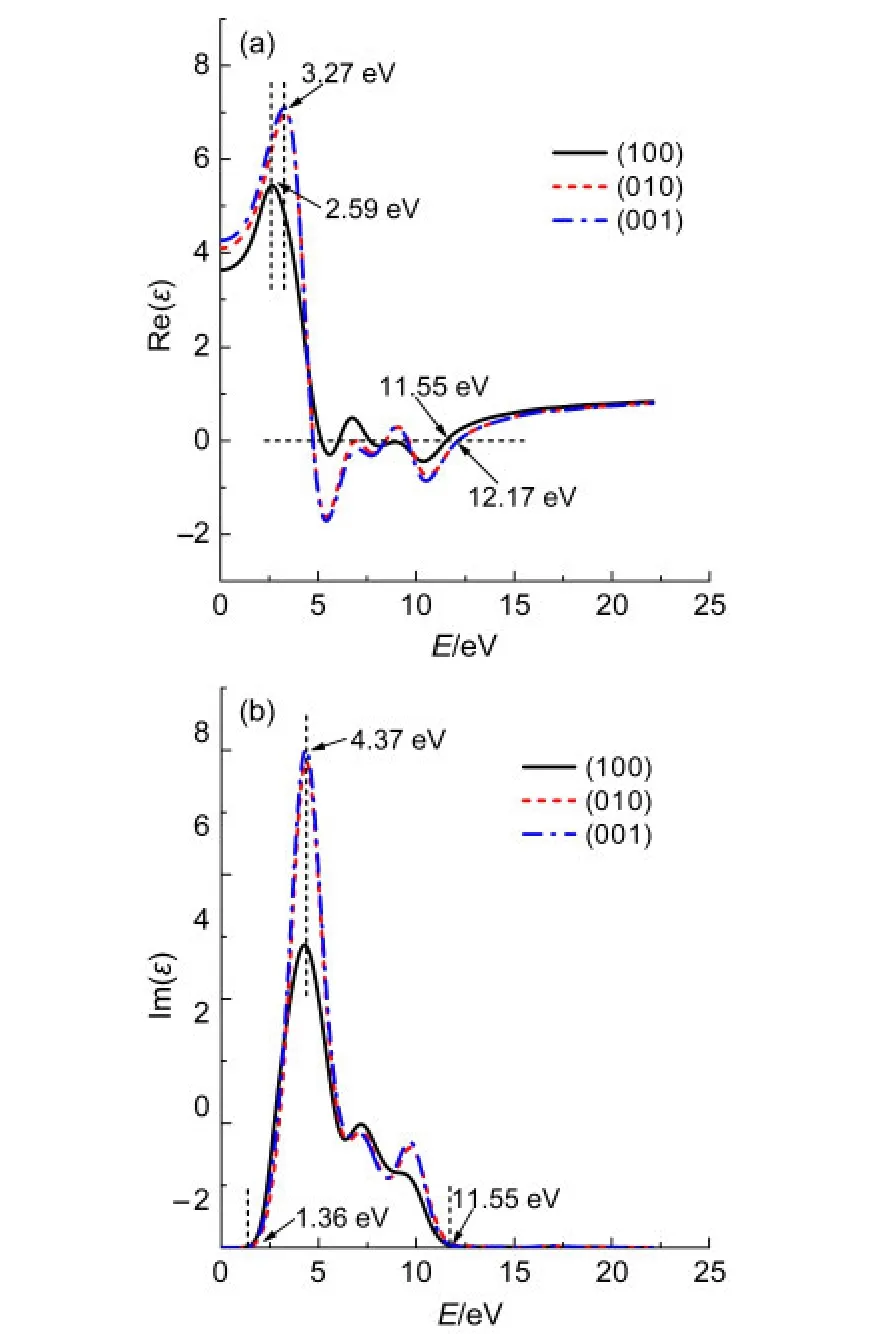
图6 碳掺杂α-S8介电函数在不同极化方向上的实部Re(ε）和虚部Im(ε）Fig.6 Real Re(ε）and imaginary Im(ε）parts of dielectric function for carbon-doped α-S8at different polarization directions

图5和图6分别为纯α-S8和掺杂α-S8的介电函数在(100）,(010）,(001）极化方向上的实部和虚部.由图5可以看到,α-S8的介电函数在(010）和(001）方向上的实部和虚部几乎完全重合.由(3）式可知,当入射光子频率一定时,介电函数的实部决定于虚部.在虚部表达式(2）中只有P与K都为矢量,且都是动量的运算符,而其他运算符都为标量,在一定条件下都为定值,所以可以推测α-S8晶体受光子激发时,在(010）和(001）方向上的动量相同.从图5中还可以看到,α-S8晶体的介电函数在(100）方向上的实部和虚部在低能区(0-5 eV）明显低于(010）和(001）方向,表明α-S8晶体在低能区(100）方向上动量低于(010）和(001）方向.α-S8介电函数在不同极化方向上的实部Re(ε）和虚部Im(ε）分别在3.45和4.40 eV出现最高峰,表明α-S8介电函数的实部和虚部在该值处的响应最灵敏.在 E≥11.68 eV和E≥12.29 eV处,α-S8在(100）方向和(010）以及(001）方向上的实部趋向于一定值,表明当能量超过该数值时,对应方向上的介电函数实部响应不变.同理,E≤2.10 eV或E≥11.74 eV时,α-S8晶体在(100）、(010）、(001）极化方向上的虚部为0.由图6可以看到C原子在α-S8晶体中掺杂后,虽然介电函数在(010）和(001）方向的实部和虚部仍高度重合,但在低能区(0-5 eV）两者发生了一定程度的偏离,(001）方向上的实部和虚部略高于(010）方向,表明α-S8晶体受低能电子激发时,在(001）方向的动量大于(010）方向.C掺杂后的α-S8晶体的介电函数在(100）方向的实部和虚部与纯α-S8相比依然小于(010）、(001）方向.掺杂后晶体在(100）方向和(010）以及(001）方向的实部分别在2.59和3.27 eV处出现最高峰,虚部在4.37 eV处出现最高峰,表明掺杂后最高峰的位置发生了红移.在E≥11.55 eV和E≥12.17 eV处,α-S8的掺杂结构在(100）方向和(010）以及(001）方向上的实部趋向于稳定,与未掺杂结构相比未出现较大变化.当E≤1.36 eV或E≥11.55 eV 时,α-S8晶体的掺杂结构在(100）、(010）、(001）极化方向上的虚部为0,相比于未掺杂结构,响应区间向低能区发生了移动.

图7 纯α-S8(a）以及碳掺杂α-S8(b）在不同极化方向上的光吸收曲线Fig.7 Absorption spectra of pure α-S8(a）and carbon-doped α-S8(b）for different polarization directions

图7所示为纯α-S8以及掺杂α-S8在(100）、(010）、(001）极化方向上的光吸收曲线,由图可知,第一,图7(a）显示,纯α-S8在(010）、(001）方向上光吸收曲线几乎完全重合,这是由于在这两个方向上介电函数重合的缘故.纯α-S8在(100）方向上的光吸收曲线强度明显低于(010）和(001）方向,但α-S8在三个方向上的光吸收波长都延伸至500 nm左右,这与实验值相吻合,13并且该值明显大于光催化剂g-C3N4的光吸收波长,1,34-36表明在可见光照射下,α-S8能利用更多的光源.纯α-S8的光吸收曲线分别在118.91、160.18和239.20 nm处出现波峰,表明波长在这三个数值下,α-S8的光吸收响应最灵敏.第二,图7(b）显示,C掺杂后的α-S8晶体在(100）方向上的光吸收曲线强度明显低于(010）和(001）方向,但三个方向上的光吸收波长都延伸至650 nm左右.与未掺杂结构相比,光吸收波长得到了极大的提高,且该值大于绝大多数的其他光催化剂及其改性材料的光吸收波长,12,37-39表明C掺杂α-S8晶体后能极大地改善材料对光源的利用率,从而提高材料的光催化效率,预示着C掺杂的α-S8材料在光催化领域有极大应用前景.C掺杂后的α-S8晶体光吸收曲线分别在120.65、163.50和240.90 nm处出现波峰,与未掺杂结构相比最灵敏响应位置发生了红移.

3.4 弹性性质

弹性常数在描述物质的机械性质方面发挥着重要作用,而密度泛函理论(DFT）能得到可靠的弹性常数数值,这已经被许多的实验研究所验证,40-44本文即使采用应力-应变的方法通过DFT得到纯α-S8以及掺杂α-S8的弹性常数,进而得到材料的体积模量、剪切模量、杨氏模量、泊松比等其他弹性性质.计算得到的纯α-S8以及掺杂α-S8的弹性常数结果如表2所示.

纯α-S8为正交晶系,C原子掺杂后的α-S8晶体晶系未发生改变,正交晶系有9个独立的弹性常数,分别为 C11、C22、C33、C44、C55、C66、C12、C13、C23,其机械稳定性条件可以定义为:45

由表2可知,纯α-S8以及掺杂α-S8晶体都完全满足以上的机械稳定性条件,表明α-S8以及C掺杂后的物质都能稳定的存在.通过已得到的弹性常数,材料的其他弹性性质,如体积模量B、剪切模量G、杨氏模量E以及泊松比γ等都可通过Voigt-Reuss-Hill(VRH）46近似方法得到,其中基于Voigt和Reuss方法得到的数值分别代表弹性模量的上下限.其计算公式如下所示:47

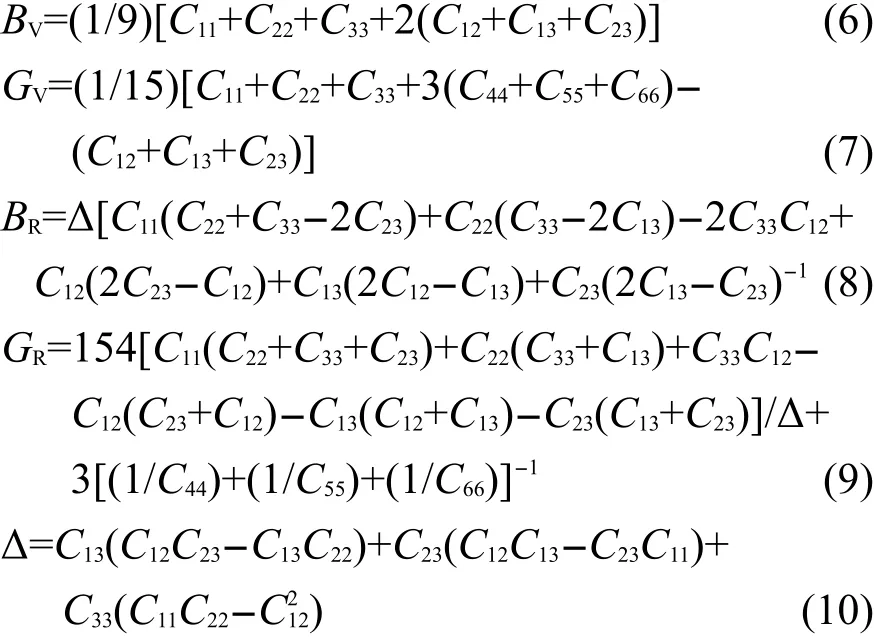
基于Hill方法得到的弹性模量可以定义为:

杨氏模量E和泊松比γ的计算公式可以定义为:

根据以上公式,得到的结果以及文献值48,49列于表3.

体积模量可用于表征材料抵抗外界压力所引起的体积改变的物理量,而剪切模量可用于衡量材料抵抗可逆形变的强弱.由表3可知,α-S8的体积模量和剪切模量都远小于非金属材料g-C3N4和石墨烯,表明α-S8在抵抗外界压力引起的材料的体积和形状发生改变的能力远不如g-C3N4和石墨烯,也即α-S8的机械性能低于g-C3N4和石墨烯,这是因为虽然g-C3N4和石墨烯为层状二维结构,其机械性质弱于它们的三维结构的同分异构体,但是相比于α-S8结构中S原子只以孤立的八元环形式存在,环与环之间无任何化学键连接,g-C3N4和石墨烯层内原子却以强的化学键相连,所以导致了α-S8的机械性能远不如层状二维结构的g-C3N4和石墨烯.C原子在α-S8中掺杂后材料的体积模量和剪切模量同时下降,说明C掺杂导致了材料机械性能的降低.观察表3可以发现,纯α-S8以及掺杂α-S8的体积模量B都大于剪切模量G,表明限制α-S8及其掺杂结构稳定性的因素是剪切模量G.在表3中,我们计算了材料的杨氏模量E,结果显示其与弹性模量和剪切模量有相同的变化规律,即α-S8材料的杨氏模量小于g-C3N4和石墨烯,掺杂C原子后α-S8的杨氏模量变小.泊松比可以用来判断材料的延展性和脆性,50当泊松比γ＜0.33时,表明该材料为脆性材料,当γ≥0.33时,则表明该材料为塑性材料.由表3可知,g-C3N4、石墨烯、α-S8以及C掺杂后的α-S8晶体都为脆性材料,且由泊松比γ越小脆性越大可知,C掺杂后的α-S8脆性减弱.根据Pugh标准,51剪切模量与体积模量的比值G/B也可以用来衡量材料的延展性,其中脆性材料的G/B≥0.5,塑性材料的G/B＜0.5.由表3可知,以上材料的剪切模量与体积模量的比值G/B均大于0.5,进一步证明了g-C3N4、石墨烯、α-S8以及C掺杂后的α-S8晶体都为脆性材料的结论.

表2 纯α-S8以及碳掺杂α-S8的弹性常数(Cij）Table 2 Elastic constants(Cij）of pure α-S8and carbon-doped α-S8

表3 基于第一性原理计算得到的体积模量(B）,剪切模量(G）,杨氏模量(E）以及泊松比(γ）Table 3 Calculated bulk modulus(B）,shear modulus(G）,and Young′s modulus(E）as well as Poisson′sratio(γ）based on first principles

3.5 各向异性

材料的各向异性的研究由来已久,最早可追溯到制陶业中,各向异性是微裂隙的主因.52本质上,现在已知的所有晶体都是弹性各向异性的,并且现在对于弹性各向异性的描述也已有多种方法.在本文中,我们引入了通用各项异性系数AU,53分别对应于体积模量和剪切模量的各向异性百分比AB、AG54以及剪切各向异性系数A1、A2、A3,54来描述纯α-S8以及掺杂α-S8的弹性各向异性.以上各弹性各向异性系数都可以通过弹性常数得到,其计算公式可定义为

处于(011）和(010）方向的(100）切面的剪切各向异性系数可以定义为:

处于(101）和(001）方向的(010）切面的剪切各向异性系数可以定义为:处于(110）和(010）方向的(001）切面的剪切各向异性系数可以定义为:

表4 纯α-S8以及碳掺杂α-S8的各向异性系数Table 4 Anisotropic factors of pure α-S8and carbon-doped α-S8

计算得到的弹性各向异性系数的结果列于表4.

对晶体而言,当各向异性系数等于0时,表明该物质各向同性,而当各向异性系数为100%时,表明该物质各向异性最大.由表4可知,α-S8的体积各向异性系数和剪切各向异性系数分别为0.0172、0.0439,接近于0,表明α-S8晶体具有强的各项同性.C掺杂α-S8后AB和AG同时变大,表明掺杂后的晶体各向同性减弱,各向异性增强.计算得到的α-S8的AU为0.4940,小于C掺杂后α-S8晶体的AU值(0.8030）,进一步证明了C掺杂α-S8后各向异性增强的结论.

对于各向同性的晶体,A1、A2、A3的值相同,当A1、A2、A3不同时,表明该晶体各向异性.由表4可以看到α-S8晶体在(100）、(010）、(001）三个切面的各向异性系数分别为0.5879、0.8368、1.5031,表明α-S8晶体在这三个切面上各向异性,且在(001）切面的各向异性强于(100）、(010）切面.C原子在α-S8中掺杂后,A1、A2、A3同时增大,但表现出与α-S8相同的变化规律,即各向异性系数A1＜A2＜A3,表明C在α-S8中掺杂后在(100）、(010）、(001）三个切面的各向异性增强,同时在(001）切面的各向异性仍是最强的.

4 结论

(1）α-S8晶体中中有4种不同对称性的S原子,计算结果显示,C原子在α-S8中的取代掺杂易于间隙掺杂,且在S3位的取代掺杂最易于进行.

(2）C原子在α-S8中掺杂后,新形成的C―S键键长变短,键重叠布居数增大,电荷密度增加,共价性增强.

(3）C掺杂α-S8晶体后,半导体的带隙变窄,晶体导电性增强;光吸收波长由原来的500 nm延伸至650 nm左右,极大地提高了材料对可见光的吸收范围,增强了催化剂的光催化效率.

(4）对纯α-S8以及掺杂α-S8的弹性性质计算显示,C掺杂后晶体的体积模量、剪切模量以及杨氏模量都下降了,表明掺杂后材料的机械性能降低,由计算的泊松比γ显示纯α-S8以及掺杂α-S8都为脆性材料.

(5）对纯α-S8以及掺杂α-S8的各向异性计算显示,C掺杂后晶体的各向异性增强,且计算结果显示纯α-S8以及掺杂α-S8在(001）切面的各向异性强于(100）和(010）切面.

(1）Wang,X.C.;Maeda,K.;Thomas,A.;Takanabe,K.;Xin,G.;Carlsson,J.M.;Domen,K.;Antonietti,M.Nat.Mater.2009,8,76.doi:10.1038/nmat2317

(2）Xiang,Q.J.;Yu,J.G.;Jaroniec,M.J.Phys.Chem.C 2011,115,7355.doi:10.1021/jp200953k

(3）Zhu,J.J.;Wei,Y.C.;Chen,W.K.;Zhao,Z.;Thomas,A.Chem.Commun.2010,46,6965.doi:10.1039/c0cc01432j

(4）Kumar,B.V.;Naik,H.B.;Girija,D.J.Chem.Sci.2011,123,615.doi:10.1007/s12039-011-0133-0

(5）Zou,Z.G.;Ye,J.H.;Sayama,K.;Arakawa,H.Nature 2001,414,625.doi:10.1038/414625a

(7）Zhang,A.P.;Zhang,J.Z.Acta Phys.-Chim.Sin.2010,26,1337.[张爱平,张进治.物理化学学报,2010,26,1337.]doi:10.3866/PKU.WHXB20100533

(8）Wang,C.Y.;Zhang,H.;Li,F.;Zhu,L.Y.Environ.Sci.Technol.2010,44,6843.doi:10.1021/es101890w

(9）Ying,H.;Wang,Z.Y.;Guo,Z.D.;Shi,Z.J.;Yang,S.F.Acta Phys.-Chim.Sin.2011,27,1482.[应 红,王志永,郭振铎,施祖进,杨上峰.物理化学学报,2011,27,1482.]doi:10.3866/PKU.WHXB20110630

(10）Ouyang,S.;Li,Z.S.;Ouyang,Z.;Yu,T.;Ye,J.H.;Zou,Z.G.J.Phys.Chem.C 2008,112,3134.doi:10.1021/jp077127w

(11）Long,B.H.;Huang,J.H.;Wang,X.C.Prog.Nat.Sci:Mater.Int.2012,22,644.doi:10.1016/j.pnsc.2012.11.007

(12）Ma,X.G.;Lv,Y.H.;Liu,Y.F.;Zhang,R.Q.;Zhu,Y.F.J.Phys.Chem.C 2012,116,23485.doi:10.1021/jp308334x

(13）Liu,G.;Niu,P.;Cheng,H.M.J.Am.Chem.Soc.2012,134,9070.doi:10.1021/ja302897b

(14）Wang,W.J.;Yu,J.C.;Xia,D.H.;Wong,P.K.;Li,Y.C.Environ.Sci.Technol.2013,47,8724.

(15）Ding,G.D.;Wang,W.T.;Jiang,T.;Han,B.X.;Fan,H.L.;Yang,G.Y.ChemCatChem 2013,5,192.doi:10.1002/cctc.201200502

(16）Dong,G.H.;Zhao,K.;Zhang,L.Z.Chem.Commun.2012,48,6178.doi:10.1039/c2cc32181e

(17）Yue,B.;Li,Q.Y.;Iwai,H.;Kako,T.;Ye,J.H.Sci.Technol.Adv.Mater.2011,12(3）,7.

(18）Íñiguez,J.;Yildirim,T.;Udovic,T.J.;Sulic,M.;Jensen,C.M.Phys.Rev.B 2004,70(6）,4.

(19）Li,Y.L.;Zhao,X.;Fan,W.L.J.Phys.Chem.C 2011,115,3552.doi:10.1021/jp1098816

(20）Yang,N.;Li,G.Q.;Wang,W.L.;Yang,X.L.;Zhang,W.F.J.Phys.Chem.Solids 2011,72,1319.doi:10.1016/j.jpcs.2011.07.028

(21）Ceperley,D.M.;Alder,B.J.Phys.Rev.Lett.1980,45,566.doi:10.1103/PhysRevLett.45.566

(22）Vanderbilt,D.Phys.Rev.B 1990,41,7892.doi:10.1103/PhysRevB.41.7892

(23）Monkhorst,H.J.;Pack,J.D.Phys.Rev.B 1976,13,5188.doi:10.1103/PhysRevB.13.5188

(24）Fischer,T.H.;Almlof,J.J.Phys.Chem.1992,96,9768.doi:10.1021/j100203a036

(25）Segall,M.D.;Lindan,P.J.D.;Probert,M.J.;Pickard,C.J.;Hasnip,P.J.;Clark,S.J.;Payne,M.C.J.Phys.:Condes.Matter 2002,14,2717.doi:10.1088/0953-8984/14/11/301

(26）Li,Q.K.;Wang,B.;Woo,C.H.;Wang,H.;Wang,R.J.Phys.Chem.Solids 2007,68,1336.doi:10.1016/j.jpcs.2007.02.035

(27）Molina,B.;Sansores,L.E.Mod.Phys.Lett.B 1999,13,193.doi:10.1142/S0217984999000269

(28）Arroyoy de Dompablo,M.E.;Biskup,N.;Gallardo-Amores,J.M.;Moran,E.;Ehrenberg,H.;Amador,U.Chem.Mater.2010,22,994.doi:10.1021/cm9018869

(29）Besancüon,K.;Laurenczy,G.;Lumini,T.;Roulet,R.;Bruyndonckx,R.;Daul,C.Inorg.Chem.1998,37,5634.doi:10.1021/ic9804162

(30）Xiao,H.;Tahir-Kheli,J.;Goddard,W.A.J.Phys.Chem.Lett.2011,2,212.doi:10.1021/jz101565j

(31）Xu,Y.;Gao,S.P.Int.J.Hydrog.Energy 2012,37,11072.doi:10.1016/j.ijhydene.2012.04.138

(32）Saha,S.;Sinha,T.P.;Mookerjee,A.Phys.Rev.B 2000,62,8828.doi:10.1103/PhysRevB.62.8828

(33）O′Donnell,M.;Jaynes,E.T.;Miller,J.G.J.Acoust.Soc.Am.1981,69,696.doi:10.1121/1.385566

(34）Yan,S.C.;Li,Z.S.;Zou,Z.G.Langmuir 2009,25,10397.doi:10.1021/la900923z

(35）Wang,Y.;Di,Y.;Antonietti,M.;Li,H.R.;Chen,X.F.;Wang,X.C.Chem.Mater.2010,22,5119.doi:10.1021/cm1019102

(36）Zheng,Y.;Liu,J.;Liang,J.;Jaroniec,M.;Qiao,S.Z.Energy Environ.Sci.2012,5,6717.doi:10.1039/c2ee03479d

(37）Niu,P.;Liu,G.;Cheng,H.M.J.Phys.Chem.C 2012,116,11013.doi:10.1021/jp301026y

(38）Tian,Y.L.;Chang,B.B.;Lu,J.L.;Fu,J.;Xi,F.N.;Dong,X.P.ACS Appl.Mater.Interfaces 2013,5,7079.doi:10.1021/am4013819

(39）Hu,Y.F.;Li,Y.X.;Peng,S.Q.;Lü,G.X.;Li,S.B.Acta Phys.-Chim.Sin.2008,24,2071.[胡元方,李越湘,彭绍琴,吕功煊,李树本.物理化学学报,2008,24,2071.]doi:10.3866/PKU.WHXB20081123

(40）Mahmood,T.;Cao,C.B.;Butt,F.K.;Jin,H.B.;Usman,Z.;Khan,W.S.;Ali,Z.;Tahir,M.;Idrees,F.;Ahmed,M.Physica B 2012,407,4495.doi:10.1016/j.physb.2012.08.006

(41）Ding,Y.C.Physica B 2012,407,2282.doi:10.1016/j.physb.2012.03.015

(42）Jiang,C.;Srinivasan,S.C.Nature 2013,496,339.doi:10.1038/nature12008

(43）Liu,M.;Lv,Z.L.;Cheng,Y.;Ji,G.F.;Gong,M.Comput.Mater.Sci.2013,79,811.doi:10.1016/j.commatsci.2013.07.024

(44）Zhang,X.D.;Ying,C.H.;Shi,G.M.;Li,Z.J.;Shi,H.F.Comput.Mater.Sci.2013,79,903.doi:10.1016/j.commatsci.2013.07.023

(45）Nye,J.F.Physical Properties of Crystals:Their Representation by Tensors and Matrices;Oxford University Press:Oxford,1985.

(46）Reuss,A.Z.Angew.Math.Mech 1929,9,49.

(47）Watt,J.P.J.Appl.Phys.1979,50,6290.doi:10.1063/1.325768

(48）Manyali,G.S.;Warmbier,R.;Quandt,A.;Lowther,J.E.Comput.Mater.Sci.2013,69,299.doi:10.1016/j.commatsci.2012.11.039

(49）Bosak,A.;Krisch,M.;Mohr,M.;Maultzsch,J.;Thomsen,C.Phys.Rev.B 2007,75,153408.

(50）Haines,J.;Léger,J.M.;Bocquillon,G.Annu.Rev.Mater.Res.2001,31,1.doi:10.1146/annurev.matsci.31.1.1

(51）Pugh,S.F.Philosophical Magazine Series 71954,45,823.

(52）Tvergaard,V.;Hutchinson,J.W.J.Am.Ceram.Soc.1988,71,157.doi:10.1111/jace.1988.71.issue-3

(53）Ranganathan,S.I.;Ostoja-Starzewski,M.Phys.Rev.B 2008,101(5）,4.

(54）Ravindran,B.;Fast,L.;Korzhavyi,P.A.;Johansson,B.;Wills,J.;Eriksson,O.J.Appl.Phys.1998,84,4891.doi:10.1063/1.368733