数学课堂教学中如何实践创新教育

庞锋

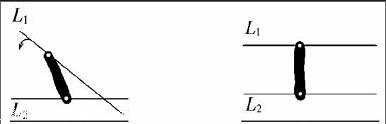
我是一名善于创新的中学数学老师，在教学中，我为了更好地培养学生的兴趣，激发学生的学习热情，常常在课堂上尝试创新教育，营造有活力、有趣味、高效的课堂，有一定的收获，愿与大家分享。

一、教师的创新意识是营造创新课堂的首要条件

教育是一个“学习—积累—运用—创新”的过程，有创新意识的教师，一定要改变以往“以知识传授为中心”的教学观念，牢牢树立“育人为先”的意识，始终把培养学生的创新素质和实践能力作为教学目标，从教学观念到教学模式上，大胆尝试，勇于实践。

二、创设问题情境，激发学生的创新思维

要激发学生的创造性思维，就应该从激发学生研究数学问题的兴趣开始，创设问题情境是激发学生学习、研究数学问题的兴趣的一个行之有效的方法。创设怎样的问题情景，才能使学生跃跃欲试、兴致勃勃呢？我们认为问题要符合学生的年龄特征和认知水平，由浅入深，逐步揭示知识的形成和发展的过程，让学生“跳一跳，可以摘到果子”，在不断地超越自己的过程中体验到成功和快乐。在教学“平行直线的概念”时，我是这样创设问题情境的：（1）出示教具，并按逆时针方向旋转直线L1；（2）让学生观察直线L1和直线L2的交点的变化情况；（3）两条直线的交点是怎样变化的呢？让学生说一说他们观察到的结果；（4）当L1旋转到图2的位置时，两条直线的交点在哪里？

图1图2

在这样的情境下，学生畅所欲言，大胆猜测，有的说图2里两条直线的交点在很远的地方，有的说图2里两条直线没有交点。这个时候教师给出两条直线平行的概念和定义，学生就比较容易接受了。更重要的是，学生在这个过程里边，经历了观察、交流、猜想，创新意识得到了强化，创新能力得到了培养。

三、注重问题的发现，在问题解决的过程中培养学生的创新能力

运用数学知识解决问题通常要经历下面四个阶段：（1）发现问题；（2）数学建模；（3）计算和论证；（4）解决问题。过去，我们在数学教学中，往往只考虑到计算和论证，对于引导学生发现问题和数学建模鲜有涉足，这样教学对于培养学生的创造性思维能力十分不利。当前，在新的课改浪潮中，我们十分重视学生的创造性思维能力的培养，注意以学生生活经验和已有的知识为依托，让学生概括出数学概念，让学生通过阅读与合作交流的方式探寻解决问题的方法。九年级上册“一元二次方程”一节，教材以介绍雕塑的问题作为引入，又介绍了无盖长方体的制作问题、篮球邀请赛的计划的制订问题。在教学中，我让学生进行了充分的阅读，并发动他们交流学习的心得。通过交流，学生发现探索解决这三个问题的共同的方法是：设未知数、找等量关系、列出方程，这个过程实际上也就是数学建模的过程。在交流的过程当中，学生还能发现这三个方程共同的特点，形成了一元二次方程的概念。通过交流，学生萌生出一个新的问题：怎样求解一元二次方程，从而求出x的值？这样教学，学生经历了数学建模的过程和从原生问题得到再生问题的过程。

四、建立新型师生关系

创新教育要求数学教师要打破传统教师讲、学生听的教学模式，重新营造民主、平等、和谐的课堂氛围。教学中，教师应尽可能地关注学生的个人体验，不歧视、不武断、不包办，把信任的阳光洒向每个角落，温暖每一个学生，让学生感受到老师春天般的爱心和热情。以积极的态度开启学生的数学思维，充分调动学生活跃的数学思维，鼓励他们乐于思考，乐于探究，尝试动手做一做。此外，数学教师还要讲究课堂教学艺术，注重培养学生的独立性和自主性，引导学生置疑、调查、探究，在实践中学习，使学习成为在教师指导下主动的、富有个性的过程，使学生成为学习的主人。数学教师要面向全体学生，由于认知、智力等不同的因素的影响，学生在掌握数学知识、提高技能等方面也存在不同程度的差异，教师在教学中要重视和承认学生的差异，因材施教，因势利导，要从学生实际出发，发展学生的优点和兴趣，优生差生同时兼顾，由浅入深、循序渐进地进行教学，一步一步地满足学生的学习需求，进而发展他们掌握及运用数学的能力。

五、借助现代化的教学技术，丰富数学课堂

新课标下的数学教学课堂是灵活的、有趣的、丰富多彩的，既要向40分钟要质量，又要减轻学生的学习负担，这种容量大、效率高的教学模式，单靠以往传统的一支粉笔、一块黑板是远远达不到教学要求的。有很多逼真的图片、立体的图像需要现代化的教学技术展示，许多数学知识的发生发展过程需要多媒体来演示。教师们在教学中，若能借助现代化的教学技术，丰富数学课堂，为课堂注入新鲜的血液，可以使学生更加直观、形象地领悟到数学知识，感受数学的奥妙与神奇。

（责任编辑韦淑红）endprint