关于丢番图方程(px+qy=2z)(200＜max{p，q}＜300)

周小娥

(海南大学信息科学技术学院，海南海口570228)

设a，b，c是正整数，指数丢番图方程

的全部整数解是丢番图方程求解中的一个十分重要的研究课题［1－2］.中外学者对方程(1)的研究主要集中在2种特殊情形:(1)a，b，c是商高数组，此时方程(1)与著名的Jesmanowicz猜想有关;(2)a，b，c取不同素数.

1958年NAGELL首先给出了max{a，b，c}≤7时方程(1)的全部非负整数解.此后直到1976年国外数学家仅给出了max{a，b，c}≤17时方程(1)的全部非负整数解.1984年孙琦、周小明给出了max{a，b，c}≤19时方程(1)的全部非负整数解.1985年杨晓卓给出了max{a，b，c}≤23时方程(1)的全部非负整数解.上述结果都是将方程(1)化为一个个具体的丢番图方程进而求解得到的，用此方法很难将max{a，b，c}推进到100.1986—1990年曹珍富［3－5］把方程(1)化为2个指数丢番图方程

与

通过先对p，q进行一些定性分析，使得求解速度得到很大提高，并得到了29≤max{a，b，c}≤97时2个方程的全部非负整数解.1991年曹珍富等［6］又给出了当100＜max{a，b，c}＜200时丢番图方程px－qy=2z的全部正整数解.2013年文献［7］给出了丢番图方程px－qy=2当200＜max{a，b，c}＜300时的全部正整数解，其中p，q为素数.虽然先对p，q进行一些定性分析，可使求解速度得到很大提高，但是在200＜max{p，q}＜300时，计算量仍然非常大.若借助计算机，则计算时间将大大减少［8－9］.笔者借助计算机，用初等方法和高等方法的结果给出200＜max{p，q}＜300时方程(3)的全部非负整数解.

1 引理及证明

为了求出指数丢番图方程

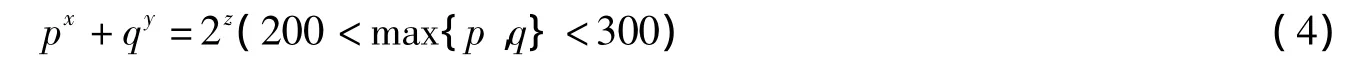
的所有非负整数解，由于方程(4)中p，q的对称性，只需给出方程(4)当1＜p＜q＜300时的所有正整数解与y=0当的非负整数解.先给出下面2个引理.

引理 1 设(p，q，x，y，z)是方程(4)的任一解，且

则满足1≤x0，y0≤36，4≤z0≤39 的所有(p，q，x0，y0，z0)由表1 和表2 给出.

证明 由于考虑的是方程(4)的正整数解，则显然有z≥4.假设x，y同时为偶数，则方程(4)可化为

对上述方程取模4，得2≡0(mod 4)，这不可能.故x，y不可能同时为偶数.

设 m≡min{4，z0}，n≡min{3，z0}. 则对于任意的奇素数 a≠3，有

于是当 p=3，200＜q＜300时，有

当3＜p＜200，200＜q＜300时，有

编写了由变量p，q，x0，y0，z0的5重循环构成的简单UBASIC程序，分别在

的范围内，对式(5)和(6)在计算机上检验得到由表1和表2给出的(p，q，x0，y0，z0).其中表1中的(p，q，x0，y0，z0)是方程(4)满足1 ＜p＜q＜300 的正整数解，表2 中的(p，q，x0，y0，z0)不是方程(4)的解，称之为方程(4)的非解的同余解.证毕.

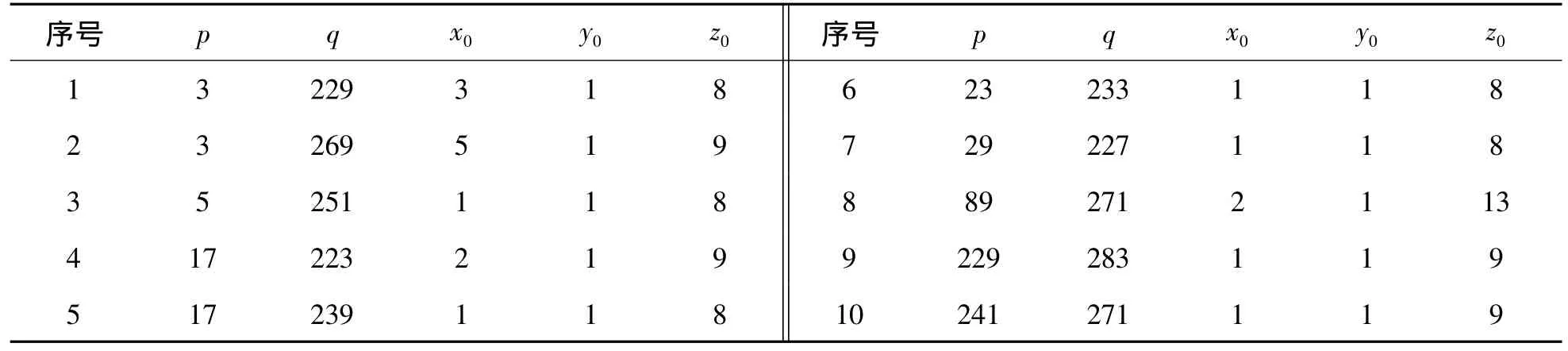
表1 方程(4)满足1＜p＜q＜300的正整数解

表2 方程(4)满足1＜p＜q＜300的非解的同余解

引理2［10］对给定的不同奇素数p，q，方程(3)至多有一组正整数解.

2 定理及证明

定理1 方程(4)的满足1＜p＜q＜300的全部正整数解(p，q，x0，y0，z0)由表1给出.

证明 假设(p，q，x，y，z)是方程(4)的解，由引理 1，令

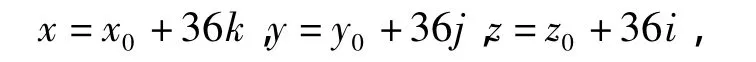
则方程(4)可化为

分2种情形来证明.

(1)(p，q，x0，y0，z0)为表 1 中任一组数. 此时，由引理 2 有 i=j=k=0.

(2)(p，q，x0，y0，z0)为表2 中任一组数. 依次用 s［t］(1≤t≤6)表示奇素数17，97，193，257，577，769，再分别用 p［t］，q［t］，r［t］表示 p36，q36，236对模 s［t］的最小正剩余，依次对式(7)取模 s［t］可得

由费马小定理知，对奇素数 p，(a，p)=1 时 ap－1≡1(mod p). 因为257 －1=4·64，769 －1=3·4·64，于是 p36，q36对模17，97，193，257，577，769 的次数均不超过 64. 因此，只要在 1≤i，j，k≤64 的范围内，对模s［1］，…，模 s［6］检验同余式(8)是否均成立. 对表2 中任一组数(p，q，x0，y0，z0)，经计算机检验没有这样的(i，j，k)存在 . 由此可知相应的(p，q，x，y，z)不是方程(4)的解 .

综合(1)与(2)，定理1得证.

注:UBASIC是适合数论研究的一种软件.UBASIC可计算的整数范围从－65 536542到65 536542，因而同余式(5)，(6)和(8)可以方便的在计算机上得到检验.

定理2 当y=0时，方程(4)的非负整数解除了以下5种情形外无其他解

证明 由题意可知，只需证明当x＞1时，方程

无解.

假设x为偶数，则方程(9)可化为(p2)x/2+1=2z.对方程(9)取模4，得2≡0(mod 4)，这不可能，故x为奇数，因此方程(9)可化为

于是 p+1=2k，2≤k≤z. 由于1 ＜p＜300 且 p为素数，可推出 p{3，7，31，127}.

当p=3时，显然z＞2，对方程3x+1=2z取模8，得3+1≡0(mod 8)，这不可能.

当 p=7 时，显然 z＞3，对方程7x+1=2z取模48，得8≡zz(mod 48)，而 zz≡32(mod 48)，矛盾.

当 p=31 时，显然 z＞5，对方程 31x+1=2z取模 960，得 32≡2z(mod 960)，而 2z≡64，128，256，512(mod 960)，矛盾.

当 p=127 时，显然 z＞7，对方程127x+1=2z取模16 128，得 128≡2z(mod 16 128)，而 2z≡256，512，1 024，2 048，4 096，8 192(mod 16 128)，矛盾. 证毕.

［1］曹珍富.丢番图方程引论［M］.哈尔滨:哈尔滨工业大学出版社，2012.

［2］潘承洞，潘承彪.初等数论［M］.北京:北京大学出版社，2013.

［3］曹珍富.关于 Diophantus 方程 ax+by=cz(Ⅱ)［J］.科学通报，1987，32(3):237.

［4］曹珍富.方程 x2+2m=yn和 Hugh Edgar问题［J］.科学通报，1986，31(7):555 －556.

［5］曹珍富.关于方程 axm－byn=2［J］.科学通报，1990，35(7):558 －559.

［6］曹珍富，佟瑞洲，王镇江.关于指数Diophantus方程的一个猜想［J］.自然杂志，1991，14(11):872－873.

［7］周小娥，邓谋杰.关于丢番图方程 px－ qy=2［J］.海南大学学报:自然科学版，2013，31(2):100 －102，105.

［8］刘静，邓谋杰.关于丢番图方程2x+2y+3z11u=3v11w［J］.黑龙江大学自然科学学报，2012，29(6):723－726.

［9］陈小燕，邓谋杰.关于丢番图方程1+5x11y+2z5u11v=2w［J］.海南大学学报:自然科学版，2014，32(1):23－27.

［10］CAO Zhenfu，CHU C I，SHIU Waichee.The exponential Diophantine equation AX2+BY2= λkZand its applications［J］.Taiwanese Journal of Mathematics，2008，12(5):1015 －1034.