脉内相位编码信号的识别与码序恢复*

刘 勇，张国毅李科学

(1.空军航空大学信息对抗系，长春130022;2.解放军94686部队，上海200000)

1 引言

在现代雷达中，相位编码[1](PSK)信号已经广泛使用。不同于通信信号，雷达中的PSK信号主要包括二相码信号(BPSK)、四相码信号(QPSK)，以及多相码(MPSK)信号。其中，BPSK信号最为常用，主要码型有巴克码、m序列等;QPSK信号的码型通常为泰勒码，由BPSK信号转化而来;常用的MPSK码型有基于线性调频信号的P1～P4码及Frank码，它们有确定的表达式，还有无确定表达式只有离散相位的码型，如多相巴克码信号。对于雷达侦察而言，需要准确而快速地获得PSK信号的种类、特征参数及编码规律，从而提供有效的电子支援。

目前，对于PSK信号的分析方法主要有瞬时自相关法[2]、相位差分法[3－4]、小波变换法[5－6]、短时傅里叶变换法[7]、循环谱法[8]、功率谱法[9]等。前两种方法都是求解相位，原理简单，运算量小，但是抗噪性较差。小波变换法相当于利用了滤波后的幅度，没有考虑相位信息，抗噪性能仍然较弱。文献[6]提出了多尺度小波的叠加，提高了抗噪性，但尺度的选择并不确定。短时傅里叶变换法适合调频信号的处理，但在低信噪比(SNR)下对PSK信号的处理效果较差。循环谱法可以处理的SNR较低，但是需要较长的码元序列，且计算量较大，也无法进行码元序列的恢复。功率谱法只适用于BPSK信号，不具有适应性。文献[10]针对MPSK几种常见的码型进行了识别，效果较好，但是码宽等参数的精度对识别的效果影响很大。

本文对相位差分法进行了改进，提高了算法的抗噪性能，并且提出了PSK信号的综合处理算法。先对信号进行带通滤波，提高对噪声的抑制作用，再采用上变频与高阶相位差分提取信号的跳变信息。通过对相位差分序列的变换与统计，实现了PSK信号的参数估计、识别及码元序列的恢复。从仿真结果来看，本文算法可以适应低SNR下对PSK信号的处理。

2 信号模型

设含有PSK信号的脉冲经采样后为

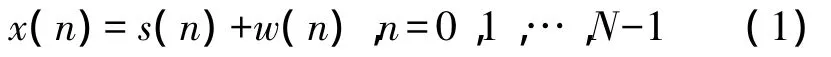
式中，w(n)为均值为零、方差为σ2的复高斯白噪声，N为采样点数，s(n)为相位调制信号，表示为

式中，A为调制信号的幅度，f0为信号的载波频率，fs为采样频率，θ0为信号的初相，θ(n)为相位调制函数。

设码元周期为Tc，则第i个码元对应的θ(n)有

对于 BPSK 信号，i∈{0，π};对于 QPSK 信号，i∈{0，π/2，π，3π/2};对于 MPSK 信号，不同码型以及不同码元长度对应下的i有不同的离散集合[10]。

3 信号识别与码元序列恢复

3.1 相位差分原理

设 (n)为x(n)的瞬时相位:

式中，Re[·]表示实部，Im[·]表示虚部，arctan[·]表示反正切。由于反正切计算出的瞬时相位的取值范围被限制在[－π，π]区间，需要进行解模糊处理[3]，得到相位p(n)。对p(n)进行一阶差分得到瞬时频率

式中，f0n为归一化的载频，f0n=f0/fs;fPSK为相位跳变引起的归一化频率，

Δε、fw为噪声引起的相位差与频率，fw=Δε/2π。

如果不考虑Δε的影响，当相位在一个码元内或者相邻码元相同时，瞬时频率等于载波频率;当相邻码元不相同时，瞬时频率会出现跳变，即含有fPSK，因此可以由f(n)的变化得到相位跳变的信息。

3.2 改进算法

在低SNR下，由于Δε的影响，利用式(6)很难提取信号的瞬时频率。因此，需要对相位差分进行改进，来提高算法的抗噪性。

(1)FIR滤波处理

由于PSK信号为窄带信号，能量在频域上比较集中，因此可以通过带通滤波抑制带外噪声。为了减小滤波后对相位的影响，采用线性相位滤波器，即FIR滤波器。设计滤波器时需要频率信息，因此先用FFT求出信号的功率谱。由于PSK信号的功率谱受码型与噪声的影响，因此对功率谱进行平滑处理。设经过平滑后功率谱P(k)最大的幅度为P(k0)，搜索幅度大于0.5P(k0)的频率，求出归一化的截止频率，以及截止频率内的频率重心，

式中，N'为 FFT的点数。归一化的码宽可粗略估计为

(2)数字上变频[4]

载频越高，Δε对f(n)的影响越小，因此将信号乘以 exp[j2π(0.5－)n]进行上变频，使变频之后信号的最大频率归一化值为 0.5，则中心频率为

(3)高阶相位差分

可以通过对相位差的平均来减小随机变量Δε对f(n)的影响。对p(i)进行M阶相位差分，再对相位差进行统计平均，得到新的瞬时频率序列f(M)(n)，

其中，Δεm为噪声引起的M阶相位差。式(9)与文献[3]中的高阶差分形式不同，由于先计算整个M阶的差分序列，再进行滑动平均，比文献[3]减少了近一半的加法计算。阶数M越高，f(M)(n)跳变的相对幅度越小，这是因为f'0n只作了一次平均，而f'PSK进行了两次平均。为了进行后续处理，对跳变相位归一化:

φ(n)的理想值在[－π，π]内，但实际值可能会超出该范围。对于差分阶数的选择，M越大，算法的抗噪性能越好。但是M一般不能大于码宽的一半，否则相邻的跳变峰值会发生交叠，可能在后续门限的判断中判为一个峰值，导致码元恢复错误。根据经验，M 一般设为

图1给出了13位二相巴克码在不同情况下的相位差分，SNR均为0 dB。图1(a)为一阶相位差分;图1(b)为M等于20的高阶差分，即文献[3]的方法;图1(c)为经过滤波和变频后的高阶差分，并进行了归一化，M也为20。与图1(a)、(b)相比，图1(c)的峰值点(圆点标记)能够正确反映巴克码的相位跳变，验证了改进算法的抗噪性能。

图1 不同情况下的相位差分Fig.1 Phase difference under different conditions

3.3 PSK信号的识别

理想状态下，在相位跳变时，BPSK信号的 φ(n)∈{－π，π}，QPSK 信号的 φ(n)∈{－π，－π/2，π/2，π}，MPSK 信号不同码型对应不同的 φ(n)，有多个跳变幅度，因此，可以根据相位跳变点来识别PSK信号以及恢复码元的变化规律。但受噪声等影响，跳变幅度有一定的起伏，因此设置相应的门限进行检测。本文设置两对门限，记为Th1P、Th1N、Th2P、Th2N，Th1P、Th1N用来检测低跳变幅度，Th2P、Th2N用来检测高跳变幅度，每对门限互为相反数。Th1P一般取值为 40°～60°，Th2P一般取值为 110°～130°。检测过第一对门限的跳变峰值，得到峰值的幅度p(i)及对应的位置I(i)，长度均为L。对p(i)进行量化，即有

图2 BPSK信号的相位差分序列Fig.2 Phase difference sequence of BPSK signal

由于PSK信号的游程为码宽的整数倍，因此我们提出用游程来剔除伪峰的方法。

(1)码宽估计

(2)伪峰剔除

在I(i)中找出第i个峰值点相邻的两个游程值Nij，计算第i个峰值的第j个游程长度(包含的码元个数)

得到相应的游程差

式中，round[·]表示四舍五入，i=1，2，…，L;j=1，2。如果C1(i)与C2(i)都大于设定的门限，则将该峰值点从包含它的所有序列及统计值中剔除，否则予以保留。

由于上述方法受门限的影响，可能不会去除所有伪峰。为了进一步提高对BPSK信号的分析能力，设定当L1＜δL时，则判为 BPSK信号，同时将所有的低跳变点当作伪峰去除，以便能正确恢复码元序列。δ一般取0.05 ～0.2。

门限为 Thv，一般取 250～300。若 V＜Thv，则判为QPSK信号，否则判为MPSK信号。

为了从MPSK信号中识别出P1～P4码及Frank码，进行模板匹配。由估计出的码宽得到码元个数

由码元个数依次恢复出P1码、Frank码的差分序列模值，分别与信号的差分序列模值进行匹配。需要说明一点，匹配只适用于一个周期的多相码。匹配度用归一化的欧式距离表示，即

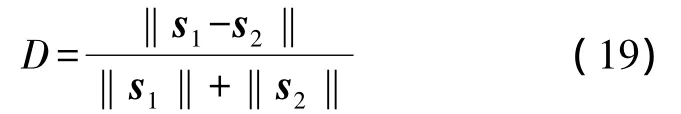
式中，s1、s2为两向量，‖·‖表示向量的模值。当D小于δ1时，取D最小值所对应的码型作为识别出的MPSK码型，分出的MPSK码型将P1/P2/P4码、Frank/P3码各分为一类;若大于或等于δ1，则将此信号判为未知码型，在人工选择后可加入到模板库，进行下次匹配处理，δ1一般取15% ～25%。

3.4 编码规律恢复

恢复BPSK、QPSK信号的编码规律，需要游程长度与跳变的相位值。游程长度式(15)已经给出，而跳变的相位值可以根据量化的跳变值求出。设上一码元相位值为a，当前码元相位值为b，则满足以下关系:

式中，mod[·]表示取余。编码规律恢复还需要信号的初相。用相位展开法获得的相位受噪声的影响，初相无法准确估计，但是不影响相对相位，本文假设初相为0。

根据前面的分析，可以得到PSK信号识别与码元恢复的流程图，如图3所示。

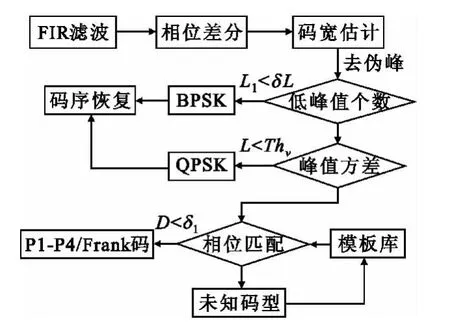
图3 PSK信号处理流程图Fig.3 Flow chart of PSK signals processing

4 仿真结果及分析

设中频采样频率为500 MHz，PSK信号的载频为 100 MHz，码宽为 0.1 μs。仿真信号中，BPSK 信号采用63位的m序列，QPSK信号采用13位的泰勒码，MPSK信号采用64位的P1码、Frank码。噪声为均值为0、方差为1的加性高斯白噪声，SNR范围为－7～5 dB，对每类信号每隔1 dB作500次Monte－Carlo实验，仿真结果如图4所示。其中，归一化均方根误差(NRMSE)定义为

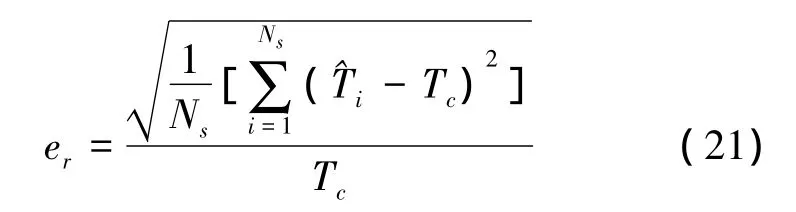
图4 码宽为0.1μs时的性能曲线Fig.4 Performance curve when code width is 0.1 μs

从图4中可以看出，在SNR大于－2 dB时，码宽估计精度很高，验证了将码宽估计的流程放在信号识别之前的合理性。本文算法对于BPSK信号的处理效果最好，在SNR大于0 dB时，基本能实现编码规律的恢复，处理效果好于文献[2－5，7]。而QPSK信号的处理效果较差是由于仿真中的信号码长较短，在峰值方差的判断中容易识别为未知信号，无法进行码元序列的恢复。实际中，QPSK信号的码长较长，其处理效果也会提高。对于仿真给出的两种MPSK信号，处理效果相近，SNR在0 dB时，识别率也接近100%。

其他仿真条件不变，将码宽增加到0.2 μs，仿真结果如图5所示。可以看出，随着码宽的增加，相应的处理性能都得到了提高。从时域上看，随着码宽的增加，单位码元的采样点也相应增加，增强了相位差分的累积，提高了信号的抗噪性。从频域上看，码宽增大，则带宽减小，相应滤波器的过渡带更窄，对噪声的抑制能力更好。

图5 码宽为0.2 μs时的性能曲线Fig.5 Performance curve when code width is 0.2 μs

5 结论

本文针对PSK信号的识别与码序恢复，对传统的相位差分方法进行了改进，进行了FIR滤波、上变频及相位差分的平均，提高了算法对低SNR环境的适应性。提出了差分序列的归一化、量化、去伪峰及匹配等处理，进一步提高了识别的准确性。本文算法不仅可以识别出常用的BPSK、QPSK信号，也能有效识别出MPSK信号。同时，本文将参数估计、识别与码序恢复进行了综合处理，可以得到PSK信号的全部特征。仿真验证了在SNR大于0 dB时，本文算法对PSK信号具有很好的综合处理效果，可以满足工程应用要求。如何将该方法运用到更多类型的雷达信号，是下一步研究的重点。

[1]Pace P E.Detecting and classifying low probability of intercept radar[M].Norwood，MA:Artech House，2009.

[2]隋莉莉，翟孝霏，陈涛，等.雷达信号有意调制的粗分类和细分类识别方法[J].现代雷达，2013，35(2):40－44.SUI Li－li，ZHAI Xiao－fei，CHEN Tao，et al.Identification method of radar signals intentional modulation on coarse and fine classification[J].Modern Radar，2013，35(2):40－44.(in Chinese)

[3]黄知涛，周一宇，姜文利.基于相对无模糊相位重构的自动脉内调制特性分析[J].通信学报，2003，24(4):153－160.HUANG Zhi－tao，ZHOU Yi－yu，JIANG Wen－li.The automatic analysis of intrapulse modulation characteristics based on the relatively non－ambiguity phase restoral[J].Journal of China Institute of Comunications，2003，24(4):153－160.(in Chinese)

[4]黄晓红，邓振淼.改进的相位展开算法及其在瞬时频率估计中的应用[J].电子学报，2009，37(10):2266－2272.HUANG Xiao－hong，DENG Zhen－miao.An improved phase unwrapping algorithm and its application to instantaneous frequency estimation[J].Acta Electronica Sinica，2009，37(10):2266－2272.(in Chinese)

[5]翟孝霏，刘雅轩，陈涛，等.一种快速雷达信号脉内调制识别分析方法[J].现代雷达，2012，34(6):16－19.ZHAI Xiao－fei，LIU Ya－xuan，CHEN Tao，et al.A fast analysis method of radar pulse modulation recognition[J].Modern Radar，2012，34(6):16－19.(in Chinese)

[6]邓振淼，刘渝.基于多尺度Haar小波变换的MPSK信号码速率盲估计[J].系统工程与电子技术，2008，30(1):36－40.DENG Zhen－miao，LIU Yu.Blind symbol rate estimation of MPSK signals based on multi－scale haar wavelet transform[J].Systems Engineering and Electronics，2008，30(1):36－40.(in Chinese)

[7]董海.基于短时傅里叶变换的相位编码信号分析[J].电讯技术，2010，50(3):18－22.DONG Hai.Phase－coded signal analysis based on STFT[J].Telecommunication Engineering，2010，50(3):18－22.(in Chinese)

[8]郑鹏，张鑫，刘锋，等.基于循环谱的MPSK信号盲检测[J].计算机仿真，2012，29(4):130－133.ZHENG Peng，ZHANG Xin，LIU Feng，et al.Blind detection of MPSK signals based on cyclic spectrum[J].Computer Simulation，2012，29(4):130－133.(in Chinese)

[9]马秀荣，张媛.基于功率谱FFT的BPSK信号参数估计[J].电子与信息学报，2013，35(5):1252－1256.MA Xiu－rong，ZHANG Yuan.Parameters Estimation of BPSK Signals Based on Power Spectral FFT[J].Journal of Electronics＆Information Technology，2013，35(5):1252－1256.(in Chinese)

[10]邓振淼，黎海林，刘渝.多相码雷达信号调制方式识别的似然方法[J].现代雷达，2009，31(12):43－47.DENG Zhen－miao，LI Hai－lin，LIU Yu.Likelihood method for recognition of polyphase－coded radar signals[J].Modern Radar，2009，31(12):43－47.(in Chinese)