基于灰色关联算法的雷达反隐身性能评估*

师俊朋，胡国平，王 馨

(空军工程大学防空反导学院，西安710051)

1 引言

从海湾战争到科索沃战争，再到伊拉克战争，隐身飞机F－117A和B－2A的出色表现引起了世界各国的高度重视。隐身飞机的出现彻底打破了原有的攻防平衡，使许多国家的防空领域出现了重大漏洞，而加强雷达反隐身性能研究也迅速成为了现代空防战争的主题。对雷达反隐身的效能评估，能为雷达的快速发展、系统优化、装备布局及作战应用提供参考和依据。但由于雷达的技术性、系统性和战场的复杂性、多变性，其性能指标综合评估势必是一个复杂的过程。目前，针对性能指标综合评估的方法主要有聚类分析法、主成分分析法、模糊物元分析法、层次分析法和相关系数法等。其中，主成分分析法虽解决了评估权重客观确定的问题，但会导致部分信息丢失;其余方法均采用主观方法确定权重，会使评价结果因人为因素而出现偏差。为保证定性分析的科学性和定量分析的准确性，本文结合隐身目标的隐身机理及空域、频域、极化域等反隐身技术原理建立了雷达性能评估指标体系，并基于常见的灰色关联算法依据信息熵理论实时计算了该算法的权重值，最后根据0－1规划模型实现了对雷达反隐身性能的优化评估。

2 雷达反隐身性能指标

隐身目标是通过降低目标的雷达散射截面积(RCS)实现隐身的。RCS不仅与目标表面导电特性、结构、材料、形体有关，还与雷达的工作频段、极化方式、目标相对雷达的空间姿态角等密不可分。雷达反隐身技术正是通过降低或弥补目标RCS的定向缩减实现的，目前该技术主要从频域、空域和极化域3个角度实现[1]。

频域反隐身是基于隐身目标对VHF/UHF和HF频段的雷达隐身效果较差的弱点实现的。目前隐身飞行器采用的RAM图层，尚不能够覆盖VHF/UHF及其以下频段，且其工作频率局限于1～20 GHz微波频段，远高于HF(5～30 MHz)频段。空域反隐身利用了隐身目标RCS只能在特定方位上降低明显的特性，雷达只要避开隐身目标RCS明显减缩的方向，从其他角度对隐身飞行器进行照射，就能保持原有作用距离上对隐身目标探测的能力。极化域反隐身是通过改变雷达发射极化方向使隐身目标的RCS达到最大值实现的。目前该技术通常与频域、空域反隐身技术结合使用，进一步增强了雷达反隐身能力。

同时，根据雷达最大作用距离方程和脉冲压缩体制雷达特点可知增大发射功率、提高天线增益、降低噪声系数、增加目标驻留时间和脉冲宽度均能弥补目标的RCS减缩效应，进而增强雷达的反隐身能力。结合上述分析，建立雷达反隐身性能评估指标体系见图1。

图1 雷达反隐身性能评估指标Fig.1 Radar anti－stealth performance indicators

对于指标A1～A5可通过查询雷达具体参数获得，对于指标A6～A8可依据以下公式计算[2]:

式中，xsi(i=1，2，…，8)表示第s部雷达系统的第Ai个指标的度量值。

3 雷达反隐身性能评估模型

灰色关联法是根据因素之间发展趋势的相似或相异程度，亦即“灰色关联度”，作为衡量因素间关联程度的一种方法。为定量分析不同雷达的反隐身性能，本文建立了基于灰色关联度的分析评估模型，见图2，图中Y表示归一化处理后的属性矩阵，通过关联度分析，得到其关于权向量W的实际关联度，经相关计算、排序即可得到评估结果U。

图2 基于灰色关联度的评估模型Fig.2 Assessment model based on gray correlation algorithm

3.1 求取归一化矩阵Y

设评估对象为m部雷达系统n个评估指标，原始数据矩阵表示为X=(xsi)m×n。为消除量纲的不一致性和增大数据的可比性，结合指标特性(A3为低优指标，其余均为高优指标)，采用相对隶属度公式对X进行归一化处理可得属性矩阵Y=(ysi)m×n，0≤ysi≤1。则ysi越大，表示第s部雷达系统的第Ai个指标评价越优;ysi越小，表示第s部雷达系统的第Ai个指标评价越差。

3.2 确定指标权向量W[3]

熵是衡量事物不确定程度的概念，熵值越大系统的不确定性就越大，反之就越小。根据熵的定义，第s部雷达的熵为

式中，psi是第s部雷达的第i个指标归一化后的权值概率。为反映不同参考向量时的权值变化，以比较序列与参考序列的差值定义相对概率。设参考序列为 y0=(c1，c2，…，c8)，则有

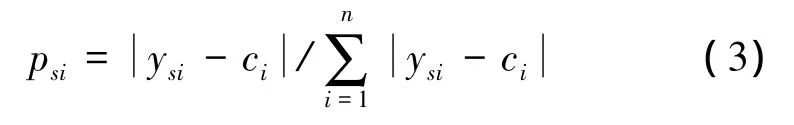
第s部雷达的熵权计算公式为

记熵权向量为 W=(w1，w2，…wm)。

3.3 求取灰色关联度

灰色关联度是对各指标的灰色关联系数加权求和得到的。根据归一化后的属性矩阵Y=(ysi)m×n分别定义系统优参考序列和次参考序列:

对于比较序列 ys=(ys1，ys2，…，ysi)，分别求取其与优、次参考序列的灰色关联系数为[4]

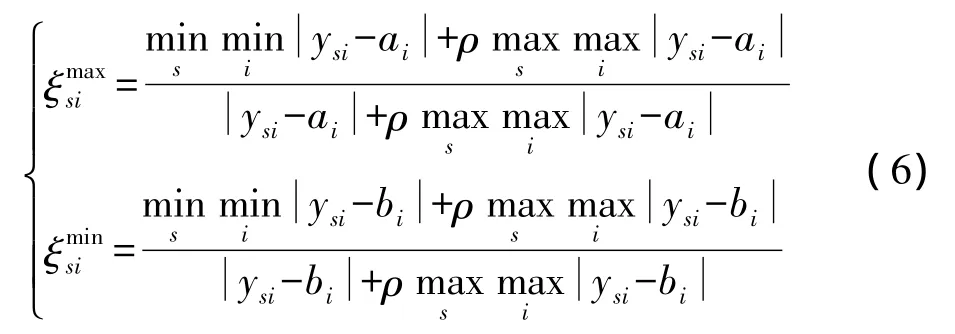
式中，ρ为分辨系数，一般取0.5。则第s个雷达系统的指标序列与优、次参考序列的关联度分别为(记为优、次关联度)

式中，wsa、wsb分别为优、次参考序列下的自适应熵权值。

3.4 建立优化评估模型

根据上述分析，γmaxs越大，雷达系统的性能指标集与优指标序列越接近，其性能越优;γmins越大，雷达系统的性能指标集与次指标序列越接近，其性能越差。所以，要提高雷达系统的性能，必须使γmaxs尽可能大，γmins尽可能小。为便于建模分析，根据式(1)将其进行归一化得

以λ1、λ2表示dmaxs、dmins的实际权重值，建立0－1规划模型:

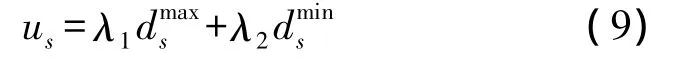
式中，λ1+λ2=1，0≤λ1，λ2≤1，us为第 s个雷达系统的最优评估值，记评估结果向量为U=(u1，u2，…us)。

为求解最佳权重值λ1和λ2，由经典最小二乘法，建立目标函数

根据拉格朗日乘数法建立拉格朗日函数

分别对λ1、λ2、λ求取一阶偏导数，并使之为0，由此可得

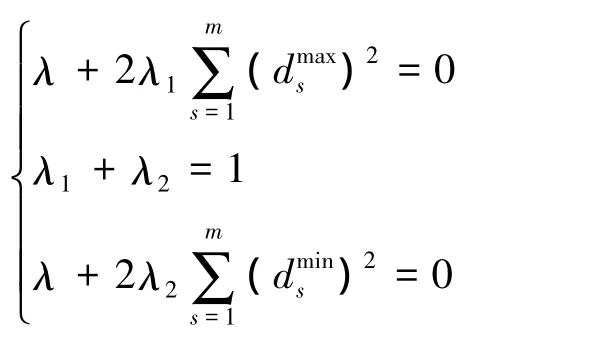
由上式求解可得最优权重值为

4 算例分析

应用上述建立的灰色关联度评估模型，对不同雷达的反隐身性能进行定量评估，各雷达具体指标数据见表 1[5]。

表1 雷达各指标参数值Table1 The indicator parameters of radar

根据公式(2)对各指标进行归一化处理，得归一化属性矩阵，见表2。

表2 评价指标的归一化数据Table2 The normalized data of evaluation indexes

以求解优关联度为例。由式(6)求取归一化序列ys=(ys1，ys2，…，ysi)与优参考序列的灰关联系数矩阵，见表3。

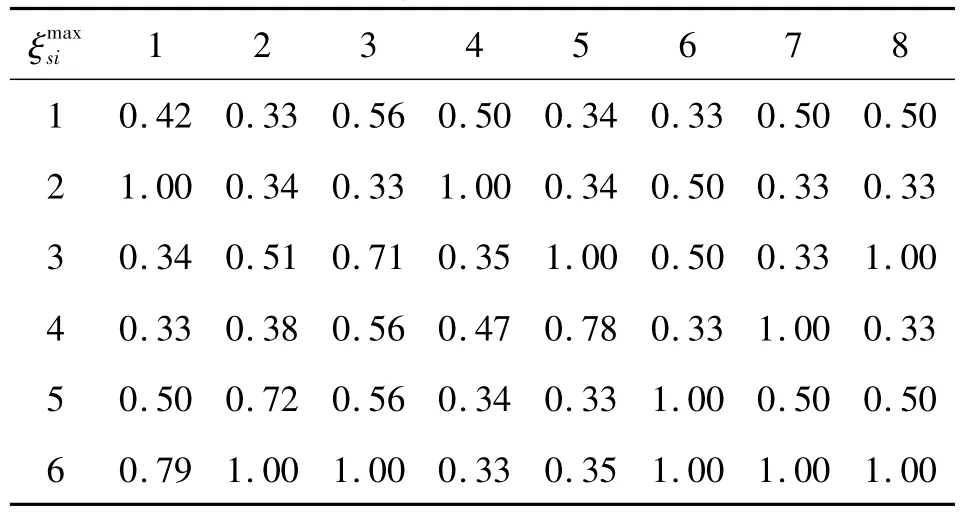
表3 灰色关联系数Table3 Grey relational coefficients

结合表3可得各部雷达的指标序列与优参考序列的优关联度为

根据式(7)将该熵权值分别与优关联度的各项对应相乘可得各部雷达的熵权关联度向量

同理可得次关联度向量为

根据式(8)将优、次关联度向量进行归一化得

随后结合式(10)可得最优权重值为λ1=0.246，λ2=0.754。最后由式(9)可得最终评价结果向量为

根据综合评估结果可知，各雷达的反隐身能力:雷达6＞雷达5＞雷达3＞雷达1＞雷达4＞雷达2。由实际数据可知，雷达6由于噪声系数小、发射功率高、垂直极化、探测视角广等使其反隐身性能较高;雷达2由于噪声系数高、探测视角小、脉宽较窄等原因使其性能相对较差。同理，对雷达1、3、4、5的数据进行定性分析发现其性能优劣与模型的评估结果基本一致，由此说明了该结论的合理、可靠、真实。

5 结束语

雷达作为有效的目标反隐身措施，越来越受到世界各国军事科技界的重视。本文给出了一种基于灰色关联度的优化评估算法，算法可以根据指标中比较序列值和参考序列值之间的关联程度自适应调整实际权值，克服了凭经验确定指标权重的主观随意性。通过对不同雷达的反隐身性能进行测试和比较说明，该算法能定量的衡量各指标的重要程度及各雷达的性能优劣。但本文的研究工作主要集中在可行性分析及理论仿真等方面，缺乏必要的工程实践和科学引导。要实现雷达反隐身性能评估的实际应用，结合工程实际、作战应用和理论创新的系统研究应是下一阶段的主要工作。为此，相关专家要努力工作，通力合作，积极开展雷达反隐身性能评估方面的研究、试验以及理论完善工作，力求为我国雷达反隐身技术的跨越发展做出贡献。

[1]李杰，付连庆.雷达反隐身技术研究[J].中国雷达，2011(2):1－7.LI Jie，FU Lian－qing.Research of Radar Anti－stealth Technologies[J].China Radar，2011(2):1－7.(in Chinese)

[2]陈永光，李修和，沈阳.组网雷达作战能力分析与评估[M].北京:国防工业出版社，2006.CHEN Yong－guang，LI Xiu－he，SHEN Yang.Radar Network Analysis and Evaluation of Operational Capability[M].Beijing:National Defense Industry Press，2006.(in Chinese)

[3]林云，司锡才.改进灰色关联算法在辐射源识别中的应用[J].通信学报，2010(8):166－171.LIN Yun，SI Xi－cai.Application of Improved Grey Correlation Algorithm on Radiation Source Recognition[J].Journal on Communications，2010(8):166－171.(in Chinese)

[4]赵晶英，陈英俊，项顺伯.物流企业遴选业务项目的熵权灰色关联算法设计[J].浙江大学学报，2012(7):484－488.ZHAO Jing－ying，CHEN Ying－jun，XIANG Shun－bo.Algorithm Design of Entropy Grey Relation for Logistics Enterprise Business Project Selection[J].Journal of Zhejiang University(Science Edition)，2012(7):484－488.(in Chinese)

[5]赵春峰，徐子闻.定量分析雷达网反隐身能力的方法[J].空军雷达学院学报，2003(3):45－47.ZHAO Chun－feng，XU Zi－wen.An Approach to the Quantitative Analysis for Anti－stealth Capability of Radar Net[J].Journal of Air Force Radar Academy，2003(3):45－47.(in Chinese)

[6]陈韬伟，金炜东，陈振兴，等.基于灰关联分析的雷达辐射源信号盲分类[J].计算机工程与设计，2009(2):4686－4689.CHEN Tao－wei，JIN Wei－dong，CHEN Zhen－xing，et al.Blind Classification of Radar Emitter Signals Based on Grey Relational Analysis[J].Computer Engineering and Design，2009(2):4686－4689.(in Chinese)

[7]王翯华，朱建军，方志耕.基于灰色关联度的多阶段语言评价信息集结方法[J].控制与决策，2013(1):109－114.WANG Yi－hua，ZHU Jian－jun，FANG Zhi－geng.Aggregation of Multi－stage Linguistic Evaluation Information based on Grey Incidence Degree[J].Control and Decision，2013(1):109－114.(in Chinese)

[8]朱银川.飞行器射频隐身技术内涵及性能度量研究[J].电讯技术，2013，53(1):6－12.ZHU Yin－chuan.Implication and Performance Metric Research of RF Stealth for Aircrafts[J].Telecommunication Engineering，2013，53(1):6－12.(in Chinese)