基于平滑RAT的多相码信号参数估计*

王晓峰，张国毅，张旭洲

(1.海军航空工程学院电子信息工程系，山东烟台264001;2.空军航空大学信息对抗系，长春130022)

1 引言

截获信号的参数估计是情报搜集活动中的一个重要环节，只有正确估计出信号调制参数才能准确地识别辐射源和产生相干干扰。多相码信号是一类由线性调频信号导出的脉冲压缩信号，兼具频率调制与相位编码的优良性能，成为目前低截获概率雷达(LPI)常用的信号形式[1－2]。因此，多相码信号的参数估计成为近来研究的热点问题[3－7]。

多相码信号产生于线性调频信号，具有和线性调频信号相似的时频特性，即在时频平面表现为几条平行的脊线，因此目前对多相码信号的参数估计主要是基于其时频特征[8－10]。文献[8]提出了多相码信号的模糊函数(Ambiguity Function，AF)检测算法，但没有研究参数估计问题。文献[9]提出了基于Radon－ambiguity变换(RAT)多相码连续波信号参数估计问题，首先估计信号扫频率，然后利用周期调制在AF时延轴上表现出的周期性估计调制周期，进而获得子码率估计。对于多相码脉冲信号，文献[10]证明了AF幅度图像中距离主脊线最近的脊线在时延轴和多普勒轴上截距分别代表信号编码周期和子码率，并且利用这一结论给出了多相编码脉冲信号编码周期和子码率估计方法。但实际电子侦察中，截获信号会不可避免地混入噪声，噪声的存在改变了RAT的峰值分布特征，对参数估计的准确性有严重影响。

针对此问题，本文首先分析了噪声对RAT特征的影响，并给出了噪声基底的产生原因，在此基础上提出了一种基于平滑RAT的多相码信号参数估计算法。该算法首先估计截获信号的噪声基底包络，然后在去除噪声基底的RAT中完成多相码信号调制参数估计。仿真结果表明，平滑RAT具有较强的抗噪性，适合于低信噪比下多相码信号的参数估计。

2 信号模型

多相码信号的解析表达式为

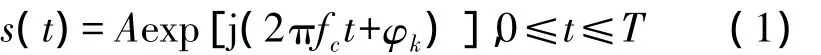
式中，A为信号幅度，fc为载频，φk为相位调制函数，T为编码周期。不同的相位调制函数代表不同的多相码信号。Frank码、P1、P2码是对步进线性调频波形的近似，采用q个频率阶跃，每个频率上采样q个离散相位。而P3、P4码是按Nyquist采样率对线性调频信号的相位进行采样[1]。令码元宽度为tb，编码长度为Nc，信号带宽为B，则多相码信号的各参数之间存在以下关系:

3 基于RAT的参数估计

信号 AF 定义为[8]

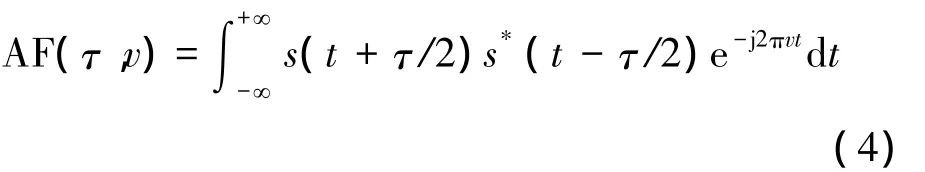
多相码信号的AF表现为多条平行的脊线，且主脊线过原点。图1为Frank码信号的AF，其他多相码信号具有类似的AF特征[4]。如图1所示，时频脊线斜率即为多相码信号调频率:

多相码信号时频脊线间隔d、带宽B和编码周期T的关系如下:

利用B和T即可得出码元宽度tb和编码长度Nc的估计值:

因此，多相码的参数估计主要是对脊线倾斜角α0和脊线间隔d的估计。

图1 Frank码AFFig.1 The AF of Frank code

Radon变换是一种广义直线积分变换，信号的RAT是AF平面内沿直线v=v0+mτ的积分:

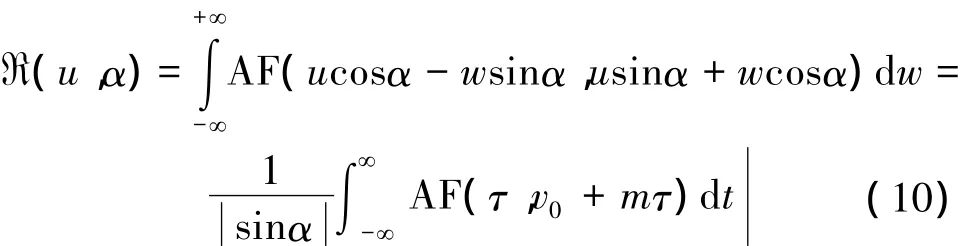
在AF平面内，多相码信号主脊线沿时间轴和频率轴的位移分别表示离散的编码周期和带宽，如图1所示。图2(a)为图1所示AF进行Radon变换的结果，搜索最大峰值位置即可得到调频率的估计值;最佳旋转角度α0切面会出现多个峰值，如图2(b)所示，峰值间距为多相码信号脊线之间的间隔d。将脊线间隔和角度α0代入式(6)～(9)即可得出码元宽度和编码个数的估计值。

由于主脊线必过原点，因此实际应用中无需计算全部Radon变换，只需要首先计算v0=0的Radon变换完成调频率的估计，然后再计算最佳旋转角度α0的Radon变换估计脊线间隔。

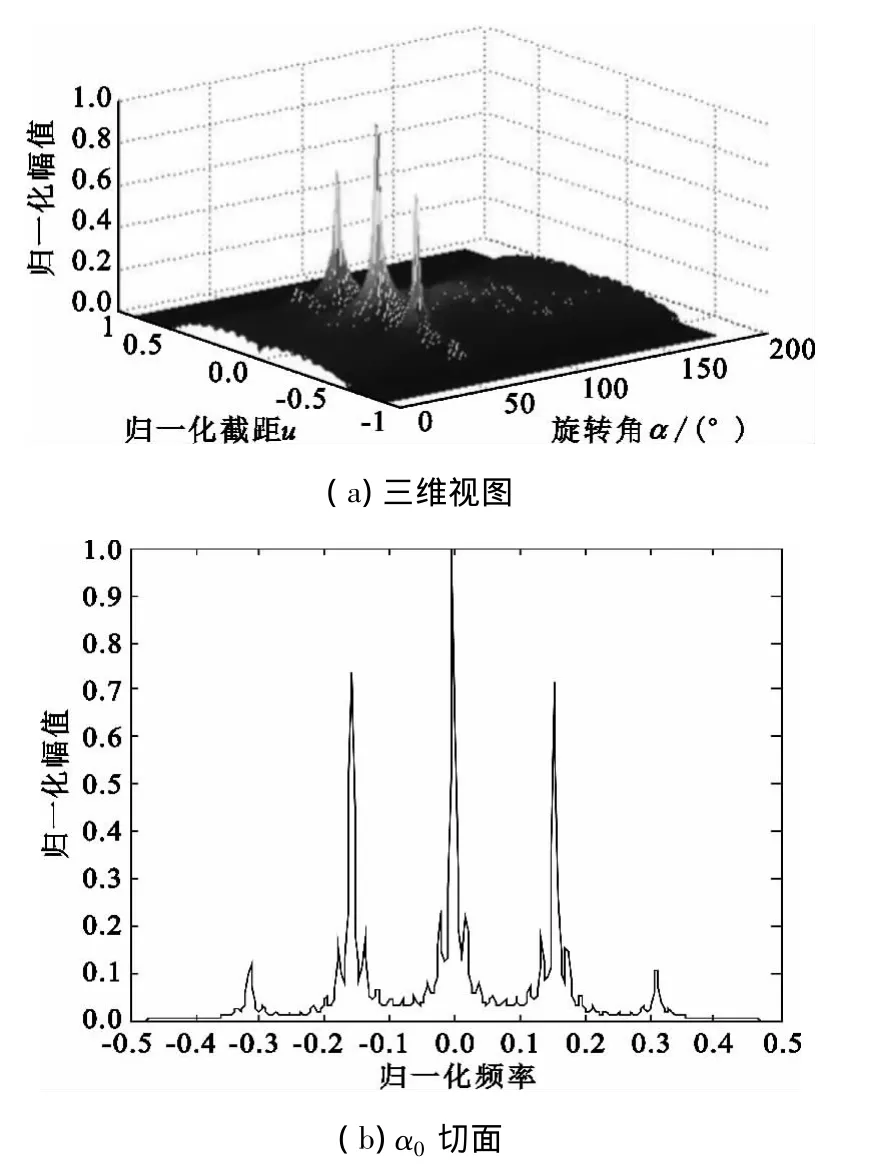
图2 Frank码RATFig.2 The RAT of Frank code

实际截获信号中会不可避免的混入噪声，实验表明RAT在处理含噪声信号时会产生十分严重的“钟形”噪声基底，如图3(a)所示。噪声基底的存在严重影响了参数估计的准确性，图3(b)为信噪比－6 dB时RAT在角度α0的切面图。

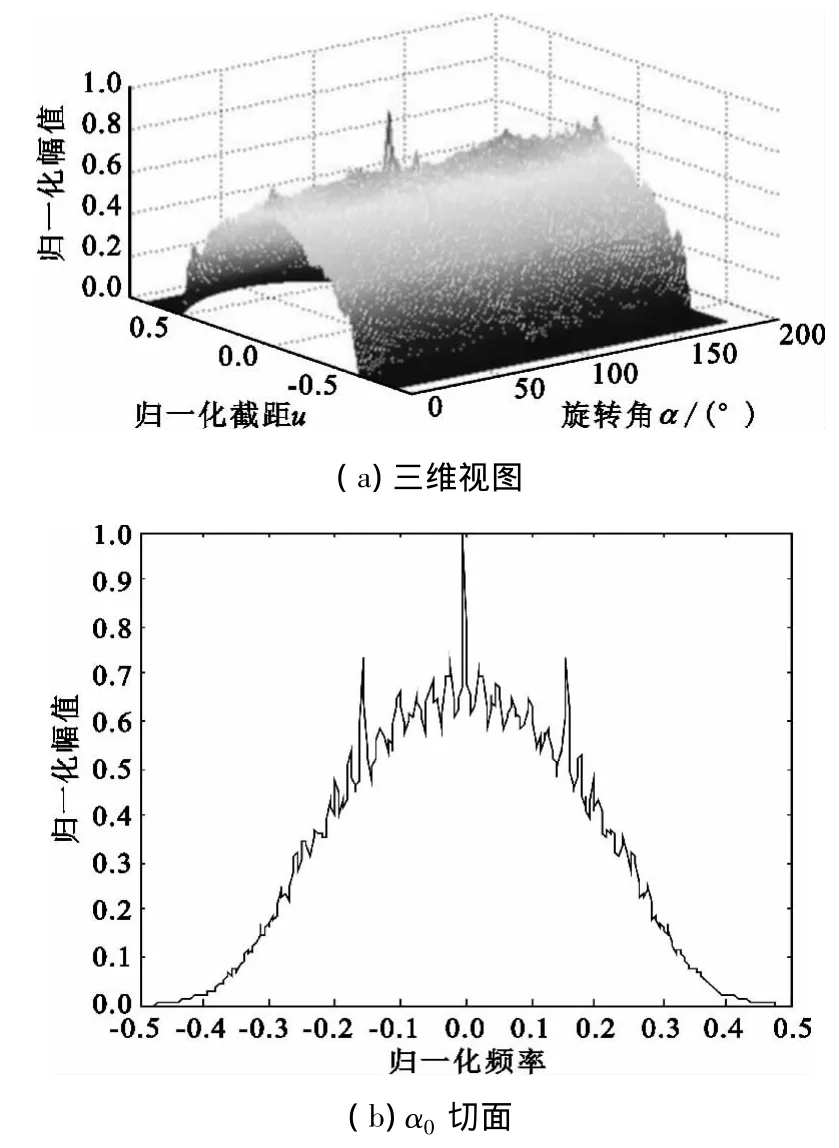
图3 含噪声Frank码RATFig.3 The RAT of noised Frank code

由图3可知信号的副脊线峰值小于噪声基底值，实际中是无法准确检测的，因此会错误估计脊线间隔，进而得出错误的码元宽度和编码长度估计值。并且随着信噪比的进一步降低，主脊线峰值同样会受到噪声基底的影响。

造成噪声基底原因有两个，一是由于信号的AF平面为矩形，使得Radon变换中不同直线的积分长度不同;二是由于有限长的噪声信号，使得噪声幅值在AF平面分布不均匀。现分别阐述噪声基底产生的原因。

信号的AF平面是一个矩形平面，这使得Radon变换中每次直线积分的长度不同。如图4(a)所示，直线l1、l2都经过坐标原点，但Radon变换中沿直线l1的积分累计大于沿直线l2的积分累计，即截距相同而不同角度的Radon变换，参与积分数据点数不同;直线l2、l3的角度相同，但Radon变换中沿直线l2的积分累计大于沿直线l3的积分累计，也就是说角度相同而截距不同的Radon变换，参与积分的数据也是不同的。因此，即使平面是幅值均为1的单位平面，随着角度与截距的变化，Radon变换的结果也不是固定的，这是产生“钟形”基底的一个原因。

理论上噪声在AF平面上是均匀分布的，不会对Radon变换的峰值产生影响，但理论分析的前提是噪声为无限长，而实际信号中的噪声都是有限长的，因此在AF平面上并不是均匀分布的。信号的AF是对信号瞬时自相关的傅里叶变换，当信号为有限长时，随着延时τ的不断增大，参与瞬时自相关运算的信号长度将不断减少，傅里叶变换后的AF幅值也会减小，这正是LFM信号的AF分布脊线呈现斜刀刃状的原因。而当信号为噪声时，AF平面呈现出中间幅值最大，向四周扩散减小的趋势，如图4(b)所示。这是“钟形”基底产生的另一个原因。

要想准确检测出信号RAT的峰值，就要去除噪声基底的影响。若已知噪声的能量，就能够根据RAT的表达式计算出噪声基底包络，然后用截获信号的RAT减去噪声基底包络即可去除噪声基底的影响，但实际截获信号的信噪比未知，因此无法给出RAT的噪声基底包络。针对此问题，本文提出一种平滑RAT方法，用以抑制噪声基底的影响，提高多相码信号参数估计的抗噪性。

图4 噪声基底原因Fig.4 The reason of noise basement

4 平滑RAT的参数估计

由于实际信号的信噪比往往是未知的，因此无法准确给出噪声基底的包络。为抑制噪声基底对多相码信号参数估计的影响，提出对信号RAT进行二次平滑，用以估计信号的噪声基底包络，然后将估计出的噪声基底从信号RAT中去除。

通过产生噪声基底原因的分析可知，任意旋转角度的噪声基底随截距的变化呈现出相同的变化规律，因此可以用α≠α0的任意角度的RAT近似噪声基底，如图3(a)所示。由于实际最佳旋转角α0未知，以及采用单一角度近似噪声基底误差较大，因此可以通过计算RAT沿旋转角度方向的均值，得出噪声基底的估计值。由图3(a)可知，信号峰值和噪声突变点会影响均值的计算，因此在计算均值之前需要对信号RAT结果进行截距方向的平滑，减少信号峰值和噪声突变点对均值的影响。

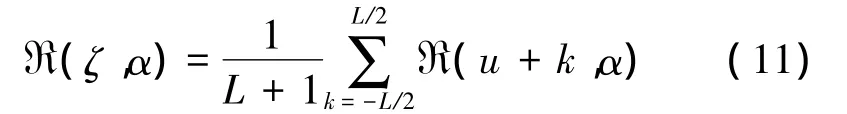
式中，L为平滑长度。

对截距平滑后的RAT计算沿旋转角度方向的均值:

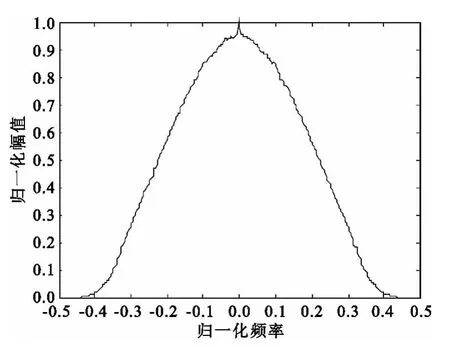
图5 噪声基底估计值Fig.5 The estimated value of noise basement

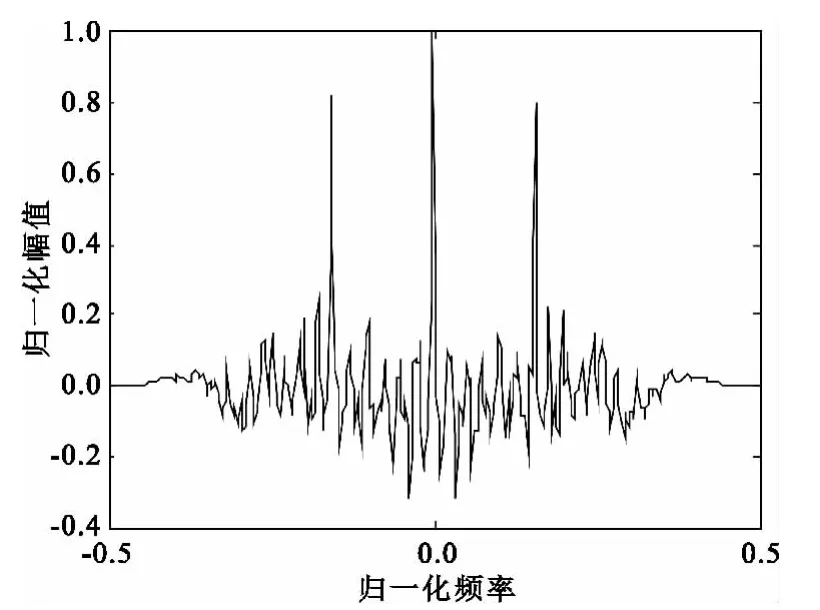
图6 平滑RAT的α0切面Fig.6 The α0section of smoothed RAT

5 仿真实验

对本文算法进行计算机仿真验证，并与文献[8]的传统RAT方法进行比较。仿真参数设置如下:编码类型为Frank码，信号载频fc=10 MHz，采样频率 fs=40 MHz，码元宽度 tb=0.1 μs，编码长度Nc=64，平滑长度L=10。信噪比从－12 dB到3 dB，步进设置为1 dB，每一个信噪比下进行500次蒙特卡洛仿真实验。分别采用传统RAT和平滑RAT估计多相码信号参数，仿真结果如图7所示。

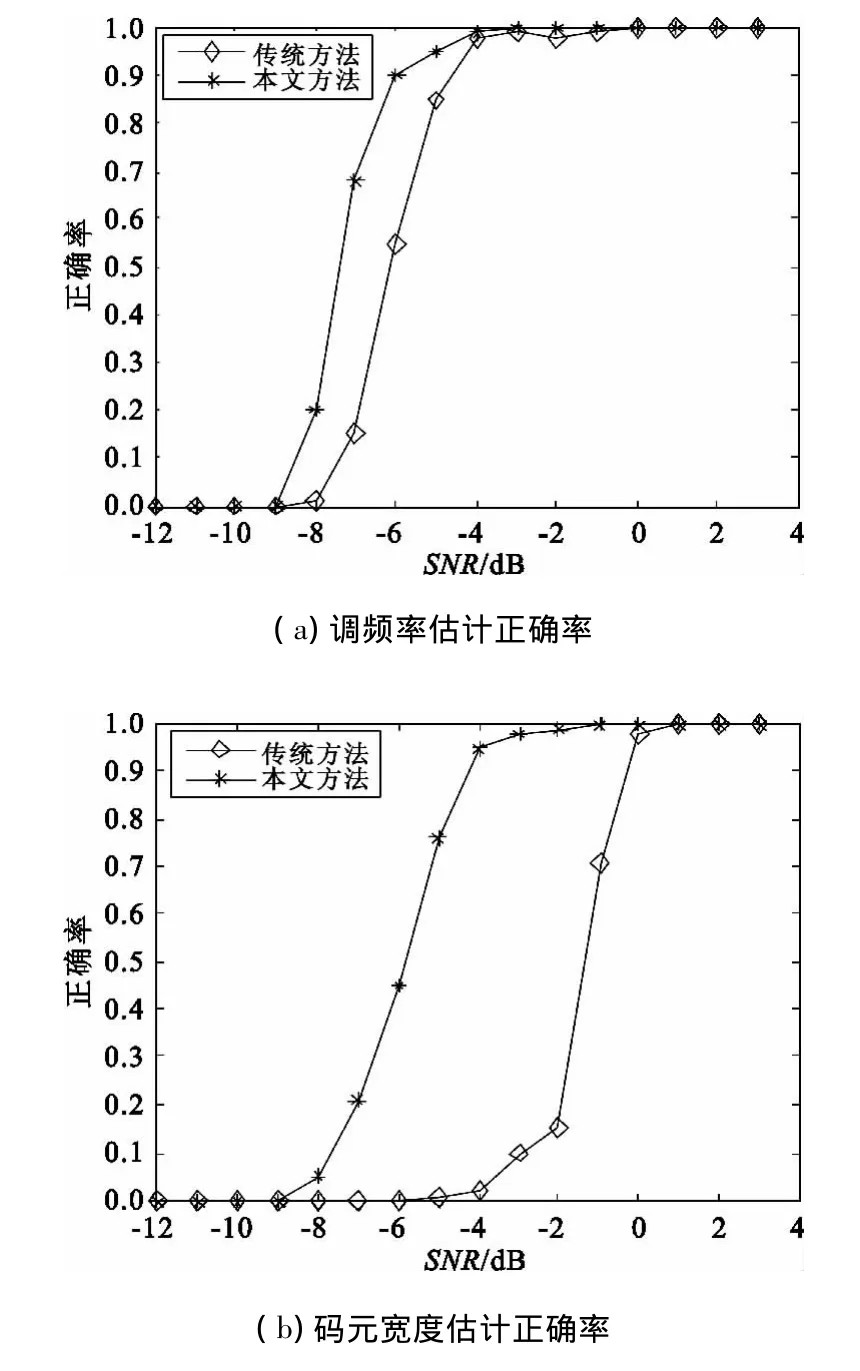
图7 参数估计正确率Fig.7 The parameter estimation accuracy

由于参数估计性能主要受到噪声基底的影响，当峰值位置正确时，则参数估计正确;若峰值位置错误，则参数估计偏差会很大，因此仿真实验中采用参数估计的正确率恒量参数估计性能，当参数估计的相对误差在0.2%内，则认为参数估计准确。由图7可以看出，本文提出的平滑RAT相比传统RAT对噪声有更强的适应性，传统方法调频率估计的信噪比门限约为－7 dB，经过平滑后调频率估计信噪比门限约为－8 dB，相比传统方法降低了1 dB，而码元宽度估计的信噪比门限相比传统方法降低了4 dB。这是由于估计调频率的多相码信号主脊线位于截距为0处，受噪声影响较小;而估计码元宽度的副脊线位于“钟形”噪声基底的半坡处，受噪声影响非常严重，因此平滑效果十分明显。仿真结果表明了本文提出的平滑RAT具有更强的抗噪性，相比传统方法能够在更低的信噪比下准确估计多相码信号的调制参数。

此外，本文还对采样精度对参数估计的影响进行了仿真测试，结果表明传统RAT与平滑RAT的参数估计精度均会随采样精度的增加而提高，但当采样精度相同时，平滑RAT参数估计的信噪比门限始终低于传统平滑RAT。

6 结束语

多相码信号是LPI雷达中常用的信号形式，截获接收机必须准确估计多相码信号的调制参数才能正确识别辐射源和产生相干干扰波形。本文研究了RAT方法估计多相码信号调制参数问题，在分析了RAT噪声基底产生原因的基础上，提出了平滑RAT方法，并以Frank码为例进行了仿真实验。仿真结果表明，改进方法相比传统RAT具有更低的信噪比门限，本文方法为实际截获信号的参数估计提供一种新的思路。

[1]Pace P E.Detecting and Classifying Low Probability of Intercept Radar[M].Norwood，MA:Artech House，2004:113－166.

[2]李军，刘娜，刘红明，等.一种基于Walsh矩阵的正交多相码设计方法[J].电波科学学报，2013，28(3):577－583.LI Jun，LIU Na，LIU Hong－ming，et al.Method of Orthogonal Polyphase Code Sequence Design Based on Walsh Matrix[J].Chinese Journal of Radio Science，2013，28(3):577－583.(in Chinese)

[3]杜清，王建.P3/P4多相码雷达信号检测与参数估计研究[J].科学技术与工程，2013(19):5673－5678.DU Qing，WANG Jian.Research of Detection and Parameter Estimation for P3/P4 Polyphase Codes Signal[J].Science Technology and Engineering，2013(19):5673－5678.(in Chinese)

[4]徐会法，胡晓峰，张明智.基于FRFT的几种典型相位编码信号检测与参数估计[J].兵工学报，2012，33(9):1048－1054.XU Hui－fa，HU Xiao－feng，ZHANG Ming－zhi.Detection and Parameter Estimation of Polyphase Code Signals Based on Fractional Fourier Transform[J].Acta Armamentarii，2012，33(9):1048－1054.(in Chinese)

[5]Akay O，Erozden E.Use ofFractional Autocorrelation in Efficient Detection of Pulse Compression Radar Signals[C]//Proceedings of 2004 International Symposium on Control Communications and Signal Processing.Hammament，Tunisia:IEEE，2004:33－36.

[6]王泽众，曹万平，刘锋，等.基于周期Wigner—Hough变换的多相编码连续波雷达信号检测算法[J].海军航空工程学院学报，2012，27(6):605－612.WANG Ze－zhong，CAO Wan－ping，LIU Feng，et al.Code Continuous Wave Radar Signal Detection Algorithm Based on Periodic Wigner－Hough Transform[J].Journal of Naval Aeronautical Engineering Institute，2012，27(6):605－612.(in Chinese)

[7]Gulum T O，Pace P E，Cristi R.Extraction of Polyphase Radar Modulation Parameters Using a Wigner－Ville Distribution－Radon Transform[C]//Proceedings of 2008 IEEE International Conference on Acoustics，Speech and Signal Processing.Las Vegas，US:IEEE，2008:1505－1508.

[8]李宏，陈绍荣，秦玉亮，等.一种多相编码脉压信号的检测与参数估计方法[J].系统工程与电子技术，2011，33(2):310－314.LI Hong，CHEN Shao－rong，QIN Yu－liang.Detection and Parameter Estimation Method for Polyphase－coded Pulse Compression Waveforms[J].Systems Engineering and Electronics，2011，33(2):310－314.(in Chinese)[9]Jennison B K.Detection of Polyphase Pulse Compression Waveforms Using the Radon－Ambiguity Transform[J].IEEE Transactions on Aerospace and Electronic Systems，2003，39(1):335－343.

[10]徐海源，黄知涛，周一宇.基于Radon变换的具有线性调频特性的多相码信号参数估计[J].信号处理，2008，24(2):172－176.XU Hai－yuan，HUANG Zhi－tao，ZHOU Yi－yu.Parameter Estimation Methods for Polyphase Codes Derived from LFM Waveforms Using the Radon Transform[J].Signal Processing，2008，24(2):172－176.(in Chinese)