一种改进的基于LC－GSC的主瓣干扰抑制方法*

张静宇，王 宇，楼大年

(空间电子信息技术研究院，西安710100)

1 引言

自适应波束形成技术可抑制副瓣干扰，关于这方面的研究已经有大量的文献[1－3]发表。然而，在现代的环境下，干扰很可能从主瓣进入，当存在主瓣干扰时，常规的自适应波束形成技术便暴露出两个严重的问题:一是主瓣严重变形，出现主瓣指向偏移，主瓣电平降低;二是旁瓣电平升高，这都严重制约了自适应波束形成在主瓣干扰条件下的应用[4]。

一般的线性约束广义旁瓣相消器中的阻塞矩阵只进行期望信号的阻塞，然后利用上下支路干扰信号的相关性通过维纳滤波对干扰进行抑制，因而可以有效地抑制旁瓣干扰，但当存在主瓣干扰时，此方法的性能通常不理想，会在干扰方向形成零点，对干扰进行抑制的同时也会影响接收有用信号。文献[5]中提出了一种利用阻塞矩阵对消主瓣干扰的方法，使用的是直接式的方法，但在信号方向有偏差的情况下对性能影响很大。

本文给出了一种基于线性约束广义旁瓣相消器的改进方法来实现对于主瓣干扰的有效抑制，与文献[5]所不同的是，本文利用了GSC框架，相比于直接式的方法，通过引入线性约束，充分发挥了GSC框架的性能优势。此方法是在线性约束广义旁瓣相消器结构之前利用阻塞矩阵对接收信号矢量进行数据预处理，预先抑制掉主瓣干扰，然后再通过线性约束广义旁瓣相消器进行数字波束形成，这样求出的自适应权矢量不需要在主瓣干扰方向形成零陷，因而不会出现主瓣变形等问题，同时还可以保持对旁瓣干扰的有效抑制。

2 信号模型

假设阵元数为N的均匀线阵，波长为λ，阵元间隔d=λ/2，1个期望信号和P个窄带干扰以平面波方式入射到阵列上，则阵列接收到的信号为

式中，si(t)，i=0，1，…，P 为期望信号和干扰的复包络;a(θi)，i=0，1，…，P 为期望信号干扰的导向矢量;N(t)为噪声信号。

假设期望信号、干扰和噪声都不相关，阵列接收信号的协方差矩阵为

实际中RX不能精确得知，通常是通过有限的K次快拍数据估计得到的，即

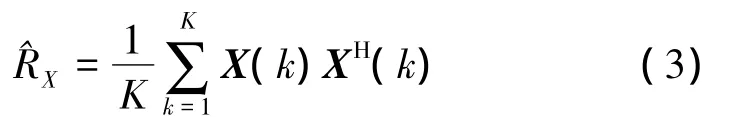
3 线性约束广义旁瓣相消器

线性约束最小方差(LCMV)波束形成器是最小方差无失真响应(MVDR)波束形成器的直接推广，而广义旁瓣相消器(GSC)与MVDR是等效的，对GSC进行推广，可得到LCMV的广义旁瓣相消形式——线性约束广义旁瓣相消器(LC－GSC)[6]。

线性约束最小方差波束形成器的权矢量可以表示为

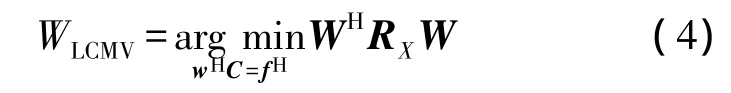
式中，C为约束矩阵，f为对应的约束响应矢量。一般地，

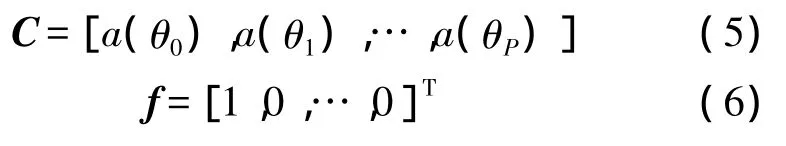
由此可以得到LCMV权矢量的直接形式:

在GSC中，静态权矢量只约束期望信号无失真，Wq=a(θ0)，如果静态权矢量满足线性约束wHC=fH，即可得到与LCMV波束形成器等效的线性约束广义旁瓣相消器，如图1所示。

图1 LC－GSC结构图Fig.1 The structure diagram of LC－GSC

线性约束广义旁瓣相消器的自适应对消干扰基于以下思想:利用已知的期望信号方向信息把阵列接收信号变换为上下两个支路，其中上支路称为主支路，通过静态权矢量Wq=C(CHC)－1f)将X(k)变换后得到参考信号d0(k)=WHqX(k)，d0(k)含期望信号和干扰;下支路称为辅助支路，通过阻塞矩阵B0阻塞掉期望信号和约束信号，通过阻塞矩阵得到X0(k)=B0X(k)，则X0(k)只含有干扰。显然，上、下支路的期望信号是相关的，通过对变换后的信号进行维纳滤波，则可自适应抵消干扰，同时上支路的期望信号被无失真输出。

这样可以得到

下支路的自适应权矢量为

由图1可以写出LC－GSC的权矢量为

因此，广义旁瓣相消器中输出的误差信号即为阵列输出，即

这里说明一下，图1中的阻塞矩阵B0为(N－1)×N维行满秩矩阵，X0(k)为(N－1)×1维向量，且B0满足

即阻塞矩阵位于期望信号导向矢量的正交补空间中。阻塞矩阵的构造方法有很多种，文献[7]的附录A中给出了两个基础简便的构造方法，本文使用的是文献[6]中给出的阻塞矩阵的构造方法:

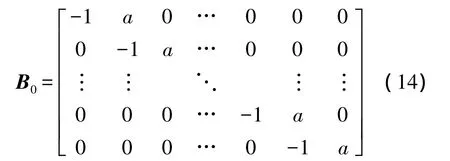
其中，a=e－j2πdsin(θ0)/λ，θ0为期望信号的入射方向。

上面分析的是主瓣内存在一个干扰的情况。当主瓣内的干扰数目大于一个时，基于数据阻塞矩阵预处理的方法依然有效，只需要对阻塞矩阵的形式进行相应的更改即可。例如，当主瓣内存在两个干扰时，阻塞矩阵B0的形式如下:

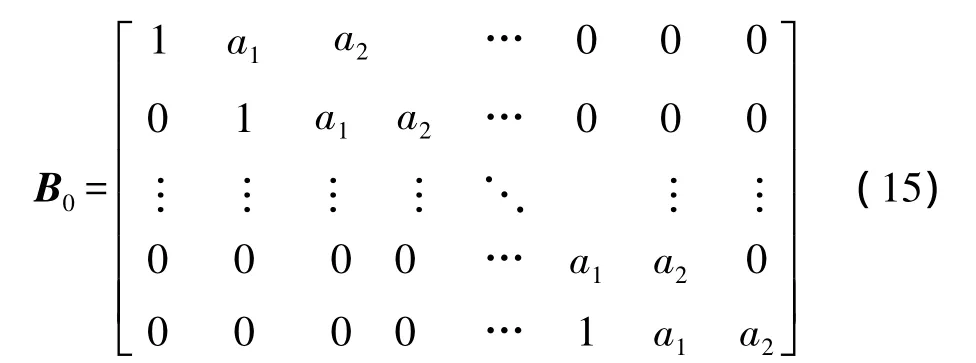
式中，B0为(N－2)×N 维矩阵，a1=－e－ju1－e－ju2，a2=－e－(ju1+ju2)，u1=2π(d/λ)sin(θ1)，u2=2π(d/λ)sin(θ2)，θ1和θ2分别为两个主瓣干扰的方向。

4 改进的基于LC－GSC的主瓣干扰抑制方法

针对LC－GSC等一般波束形成技术都无法有效解决在抑制主瓣干扰的同时又可以保证主瓣不发生畸变等诸多问题，本文给出了一种新的结构，如图2所示。

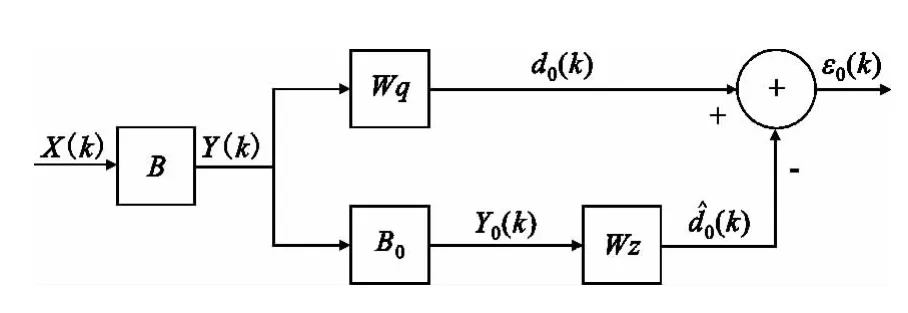
图2 本文方法的BLOCK－GSC结构框图Fig.2 The proposed BLOCK－GSC structure diagram

可以看出，本方法是在标准LC－GSC结构前增加一个阻塞矩阵B，通过阻塞矩阵预先实现对于主瓣干扰的抑制，然后再进行数字波束形成，同时完成对于旁瓣干扰的抑制。阻塞矩阵的具体结构根据主瓣内的干扰数目而定，当主瓣内为一个干扰时，B是(N－1)×N维矩阵，其结构如下所示:

其中，b=e－j2πdsin(θ1)/λ，θ1为主瓣干扰的方向。

采用这种形式的阻塞矩阵，是由于主瓣干扰的导向矢量为

其中，m=1，2，…，N－1，即

因而

继续前面的推导，经过阻塞矩阵B可以得到

式中，Y(k)为(N－1)×1维向量。阻塞矩阵之后的结构与标准的LC－GSC结构相同，只是上支路的静态权矢量Wq选取(N－1)维。

上支路经过静态权矢量后得到

由于 Ba(θ1)=0，可以得到

同时，下支路的阻塞矩阵B0采用与矩阵B相同的结构形式，只需将其中的θ1变为期望信号的方向θ0，同时由于Y的维数变为(N－1)维，因而阻塞矩阵 B0的维数为(N－2)×(N－1)。

最终可以得到

这样在上下支路进行维纳滤波前，上支路d0(k)中含有期望信号，旁瓣干扰信号和噪声，下支路Y0(k)中只含有旁瓣干扰信号的噪声。通过维纳滤波，上下支路相关的干扰信号实现对消，就可以得到无失真的期望信号。

通过这种方式得到的自适应权矢量完全不需要在主瓣内的干扰方向上形成零陷，保证了主瓣指向的精确性，提高了对接收信号的增益，为保证可靠稳定的通信奠定了坚实的基础。

从图3中可以看出，LC－GSC在所有干扰的方向(－55°、－ 35°、3°、15°、65°)上均形成了零陷，包括主瓣内3°方向上的主瓣干扰，所有的零陷深度基本在－50 dB左右。然而，在主瓣内形成的零陷导致主瓣电平降低，波束指向偏移，同时旁瓣电平升高，从图中可以看出，主瓣波束指向偏移了约2°，电平下降了约2 dB，同时第一旁瓣电平约为－6 dB。BLOCK－GSC同样在所有旁瓣干扰处均形成超过－60 dB的零陷，从图中可以看出，自适应方向图主瓣指向为0°，主瓣电平为－0.3 dB，第一旁瓣电平为－13 dB，且所有旁瓣电平均较 LC－GSC低10 dB左右，原因是由于不需要在主瓣内的干扰处形成零陷，因而保证了主瓣的形状，同时获得了性能更好的旁瓣电平效果。

仿真2:此仿真是对比存在两个主瓣干扰(入射角为－2°和 3°的干扰)时 LC－GSC 和 BLOCK－GSC两种方法的自适应方向图，仿真结果见图4。

5 仿真分析

主要针对LC－GSC和BLOCK－GSC两种方法进行仿真，通过自适应方向图和输出信干噪比曲线图对比分析两种方法的性能。仿真模型选择常使用的16个阵元半波长等距线阵，有5个互不相干的干扰信号分别由－55°、－ 35°、3°、15°和 65°入射到阵列上，由于主波束主瓣宽度约为10°，故主瓣内存在一个干扰，干扰的信干噪比均为40 dB，目标信号方向为0°，信噪比为0 dB，快拍数为48。

仿真1:此仿真是对比存在一个主瓣干扰(入射角为3°的干扰)时LC－GSC和BLOCK－GSC两种方法的自适应方向图，仿真结果见图3。

图4 两个主瓣干扰的自适应方向图的对比Fig.4 The comparison diagram of adaptive pattern of the two methods with two mainlobe interferences

通过图4中可以看出，主瓣内存在－2°和3°两个主瓣干扰，LC－GSC由于在主瓣内形成了两个－50 dB深度的零陷，因而导致主瓣电平下降到－15 dB，第一旁瓣电平抬升至－3 dB，主瓣已完全被旁瓣淹没，而BLOCK－GSC由于不需要在主瓣内形成零点，因此保持了良好的方向图效果。从图中可以看出，主瓣电平为－0.6 dB，第一旁瓣电平为－14 dB，且各旁瓣干扰处的零陷深度均超过了－50 dB。

仿真3:此仿真是对比两种方法对于主瓣内存在一个干扰，且干扰方向从－3°到+3°滑动过程中得到的自适应方向图，移动间隔为0.1°，仿真结果见图5和图6。

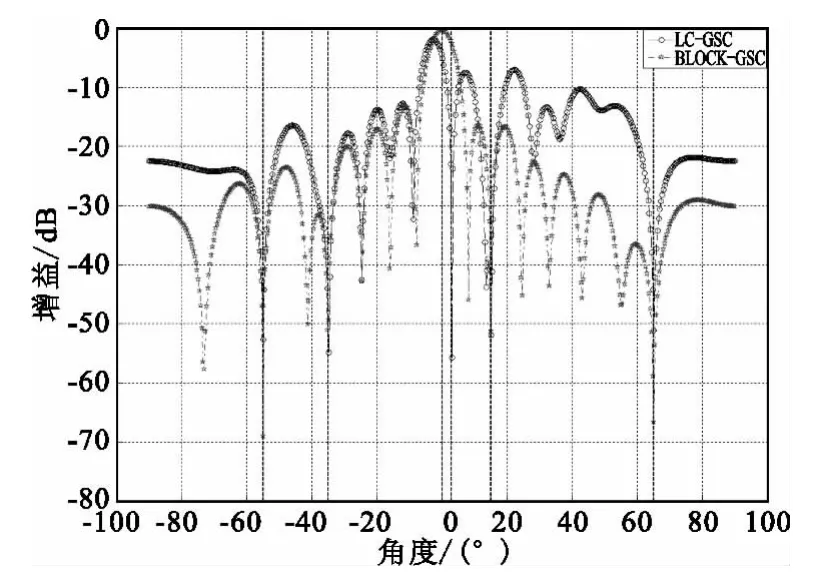
图3 一个主瓣干扰的自适应方向图的对比Fig.3 The comparison diagram of adaptive pattern of the two methods with one mainlobe interference

由图7中可以看出，BLOCK－GSC获得了比LC－GSC更好的输出信干噪比效果，原因是LC－GSC方法得到的自适应权在主瓣干扰方向也形成了零点，造成了方向图主瓣变形，虽然抑制了干扰，但同时也降低了对于期望信号的接收增益;BLOCK－GSC由于在GSC结构前已经通过阻塞矩阵将主瓣干扰从接收数据中消除，实现了对于主瓣干扰的抑制，因而其输出信干噪比要明显优于LC－GSC。

图5 LC－GSC结构下主瓣干扰由－3°到+3°变化的自适应方向图Fig.5 The adaptive pattern of LC－GSC with the mainlobe changing from －3°to+3°

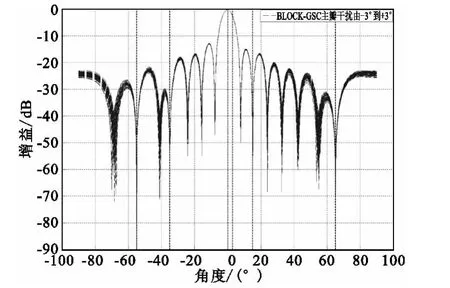
图6 BLOCK－GSC结构下主瓣干扰由－3°到+3°变化的自适应方向图Fig.6 The adaptive pattern of BLOCK－GSC with the mainlobe changing from －3°to+3°

从图5和图6中可以看出，无论干扰存在于主瓣内的哪个方向，BLOCK－GSC都可以很好地保证主瓣的波束形状，从而保证了通信系统良好的增益效果。

仿真4:此仿真是对比LC－GSC和BLOCK－GSC两种方法的输出信干噪比随输入信噪比的变化曲线，输入信噪比为－15～25 dB，间隔为1 dB，快拍数为1 600，仿真结果见图7。

图7 输出信干噪比随输入信噪比的变化曲线Fig.7 The curve of output SINR vs.the input SNR of the two methods

6 结论

提出了基于线性约束广义旁瓣相消器的改进方法，利用阻塞矩阵对接收信号数据的预处理，消除了主瓣内干扰的影响，因此自适应波束形成不会对主瓣范围内干扰进行零陷抑制，从而不会导致主波束变形及副瓣电平升高，相比LC－GSC算法输出信噪比改善了近4 dB。并且，针对主瓣内不同的干扰数目，利用不同形式的阻塞矩阵，亦可得到性能良好的自适应方向图。此方法需要精确已知期望信号的方向和需要阻塞干扰的数目及其入射角度，对于实际应用中存在的阵列误差，可以配合使用误差校准技术。另外，利用对角加载、方向导数约束以及最差性能优化等技术也可以在方向未精确已知的情况下进行性能补偿，从而增加了算法的鲁棒性，大大加强了其工程实际应用的有效性和可靠性。

[1]SU Baowei，WANG Yongliang，ZHOU Liangzhu.A mainlobe interference canceling method[C]//Processings of 3rd International Conference on Signal Processing.Beijing:IEEE，2005:23－26.

[2]覃岭，黄茜，李会勇.主瓣干扰下宽带圆阵自适应波束形成方法[J].电子科技大学学报，2009，38(3):359－362.QIN Ling，HUANG Xi，LI Hui－yong.Adaptive Broadband Beamforming of Circular Array Under Main Lobe Interference Condition[J].Journal of University of Electronic Science and Technology of China，2009，38(3):359 －362.(in Chinese)

[3]Hughes D T，Mcwhirter J G.Using the penalty function to cope with mainlobe jammers[C]//Processings of 3rd International Conference on Signal Processing.Beijing:IEEE，1996:461－464.

[4]Jablon N K.Adaptive beamforming with the generalized sidelobe canceller in the presence of array imperfections[J].IEEE Transactions on Antennas and Propagation，1986，34(8):996－ 1012 .

[5]苏保伟，王永良，李荣峰，等.阻塞矩阵方法对消主瓣干扰[J].系统工程与电子技术，2005，27(11):1080－1083.SU Bao－wei，WANG Yong－liang，LI Rong－feng，et al.Mainlobe interference cancelling method via block matrix[J].Systems Engineering and Electronics，2005，27(11):1080－1083.(in Chinese)

[6]王永良，丁前军，李荣峰.自适应阵列处理[M].北京:清华大学出版社，2009.WANG Yong－liang，DING Qian－jun，LI Rong－feng.A-daptive Array Processing[M].Beijing:Tsinghua University Press，2009.(in Chinese)

[7]Goldstein J S，Reed I S，Scharf L L.A Multistage Representation of the Wiener Filter Based on Orthogonal Projections[J].IEEE Transactions on Information Theory，1998，44(7):2943－2959.