GF(3)上两类广义自缩序列的伪随机性*
2018-09-03徐玉春王锦玲
徐玉春,王锦玲
(1.郑州铁路职业技术学院,河南 郑州 451460;2.郑州大学 数学与统计学院,河南,郑州,450001)
0 引 言
信息时代中,伪随机序列被广泛应用于通信领域,而序列密码的设计准则总是高度安全和简单结构的统一。Willi Meier[1]提出的自缩序列因结构简单而引人入胜,颇受关注;胡予璞等人在此基础上又给出了广义自缩序列的定义,并在GF(2)上研究并证明了此定义下广义自缩序列的许多密码学性质,如0-1分布的均衡性等[2-6]。本文则在GF(3)上讨论两类广义自缩序列的伪随机性质,得到这两类序列的游程分布及其一致且近似相等,且最小周期都达到最大2·3n-2。
定义1:设a∞=a0a1a2……是GF(3)的n级m-序列,其周期为3n-1。现定义两类广义自缩序列如下:
①如果ak=1,则输出ak-2;如果ak=2,则输出ak-2+ak+1;否则,不输出;
②如果ak=1,则输出ak-2;如果ak=2,则输出ak-2+ak-1+ak+1;否则,不输出;
把由①得到的序列记为b1∞,把由②得到的序列记为b2∞
。可以看到,①和②是两类不同输出序列。为了使文章更精炼而又不影响读者理解,现只对①序列的1长游程分布只列出1长0-游程分布。记0m、0s分别为长度m、s长的0串,其中长度m、s可以取0;“*”表示GF(3)上的任意值。
1 序列b∞的游程分布
首先考虑序列b1∞的长度为1的0-游程。
引理1:设某个固定的t,使得at=at-2=0,此时对应序列b∞的一个输出比特bs=at-2=0,且要得到序列b∞的长度为1的0-游程。
当且仅当,在以下17种情形下得到101:
(1)1*100m0100s021(2)1*100m0101
(3)1*100m01020(4)1*100m0121
(5)1*200m0100s021(6)1*200m0101
(7)1*200m01020(8)1*200m0121
(9)101100m021(10)101101(11)1011020
(12)10111(13)101120(14)002100m021
(15)002101(16)0021020(17)002122
当且仅当,在以下17种情形下得到201:
(1)2*100m0100s021(2)2*100m0101
(3)2*100m01020(4)2*100m0121
(5)2*200m0100s021(6)2*200m0101
(7)2*200m01020(8)2*200m0121
(9)201100m021(10)201101(11)2011020
(12)20111(13)201120(14)102100m021
(15)102101(16)1021020(17)102122
当且仅当,在以下13种情形下得到102:
(1)1*100m0100s022(2)1*100m01021
(3)1*100m0122(4)1*200m0100s022
(5)1*200m01021(6)1*200m0122
(7)101100m022(8)1011021(9)101121
(10)002100m022(11)0021021(12)00211
(13)002120
当且仅当,在以下13种情形下得到202:
(1)2*100m0100s022(2)2*100m01021
(3)2*100m0122(4)2*200m0100s022
(5)2*200m01021(6)2*200m0122
(7)201100m022(8)2011021(9)201121
(10)102100m022(11)1021021(12)10211
(13)102120
引理2:设某个固定的t,使得at=2,at-1+at+2=0。此时,对应序列b∞的一个输出比特bs=at-1+at+2=0,且要得到序列b∞的长度为1的0-游程。
当且仅当,在以下12种情形下得到101:
(1)1*100m0200s021(2)1*100m02022
(3)1*200m0200s021(4)1*200m02022
(5)101200m021(6)1012022(7)202200m021
(8)2011022(9)1*10221(10)111220
(11)212222(12)12121
当且仅当,在以下12种情形下得到201:
(1)2*100m0200s021(2)2*100m02022
(3)2*200m020021(4)2*200m02022
(5)201200m021(6)2012022(7)002200m021
(8)0022022(9)2*0s10221(10)211220
(11)012222(12)22121
当且仅当,在以下16种情形下得到102:
(1)1*100m0200s022(2)1*100m0201
(3)1*100m02020(4)1*200m0200s022
(5)1*200m0201(6)1*200m02020
(7)101200m022(8)101201(9)1012020
(10)202200m022(11)202201(12)2022020
(13)1*10222(14)111221(15)212220
(16)22221
当且仅当,在以下16种情形下得到202:
(1)2*100m0200s022(2)2*100m0201
(3)2*100m02020(4)2*200m0200s022
(5)2*200m0201(6)2*200m02020
(7)201200m022(8)201201(9)101200m20
(10)002200m022(11)002201(12)0022020
(13)2*10222(14)211221(15)012220
(16)02221
定理1:设序列b1∞的长度为1的0-游程的个数为u,则:

以同样的分析方法,得:
定理2:设序列b1∞的长度为1的1-游程的个数为u,则:
定理3:设序列b1∞的长度为1的2-游程的个数为u,则:
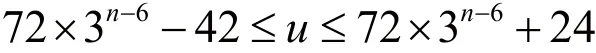
定理4:设序列b2∞的长度为1的0-游程的个数为u,则:
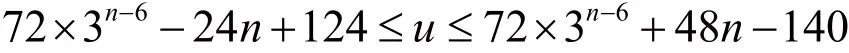
定理5:设序列b2∞的长度为1的1-游程的个数为u,则:
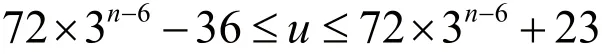
定理6:设序列b2∞的长度为1的2-游程的个数为u,则:

2 序列b∞的最小周期
引理3:在输出序列b∞的一个周期P内,若有k长1-游程出现的次数为N,且满足gcd(N,P)=1,则P是序列b∞的最小周期。
证明:参见文献[7]。
为了得到序列b1∞的最小周期,由序列b1∞游程分布可得:
引理4:输出序列b1∞中出现n+1长的1-游程时,m-序列a∞中有以下一种情况出现:
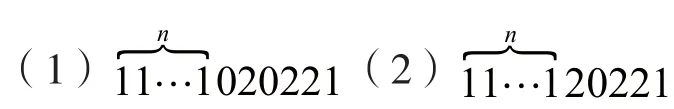
引理5:输出序列b1∞中出现n长的1-游程时,m-序列a∞中有以下一种情况出现:

定理7:m-序列a∞控制输出的序列b1∞有最小周期2×3n-1。
证明:由输出序列的形式可知,2×3n-1是输出序列b1∞的一个周期。又由m-序列a∞中没有大于n长的1-游程,故考虑以下几种情况。若序列b1∞在一个周期2×3n-1中出现了n+1长的1-游程,则一定是在引理4中m-序列a∞控制输出的比特串中出现,因m-序列a∞中n长1-游程仅出现一次,故比特串在m-序列a∞中有且仅有其中之一出现;若序列b1∞在一个周期2×3n-1中出现了n长的1-游程,则一定是在引理5中m-序列a∞控制输出的比特串中出现。由m-序列性质知,(1)(2)与(3)(4)不能同时出现。由线性递归序列的表达式知,(1)(2)在m-序列a∞中有且仅有其中之一出现;同理,(3)(4)也如此。于是,可知序列b1∞中出现的n长的1-游程仅出现一次。再由引理3可知,2×3n-1是输出序列b∞的最小周期。
定理8:m-序列a∞控制输出的序列b2∞有最小周期2×3n-1。
证明:同定理7的证明方法,要先分析序列b2∞中最长的1-游程,根据1-游程的个数与2×3n-1互素得序列b2∞的最小周期为2×3n-1。
3 结 语
先列出GF(3)上几类广义自缩序列的输出序列与本文的一类广义自缩序列在最小周期都达到2×3n-1内的游程分布情况表,如表1所示。

表1 本文游程分布情况与其他文献游程分布情况
从表1可以看到,本文构造的两类广义自缩序列长游程少,0、1、2游程分布均匀。研究表明,这两类广义自缩序列b∞暴露的驱动信息少,对驱动序列a∞有很高的保护强度,适合在通信和计算机编码系统中应用,并与GF(3)上其他广义自缩序列相比具有更好的密码学特性[8-11]。
