基于行为规律的搜索资源分配新算法*

褚衍杰，徐正国

(盲信号处理重点实验室，成都610041)

1 引言

在第二次世界大战期间，由于战争中快速搜索对方运动目标的需要，George Kimball、Bernard Koopman等人创立了最优搜索理论，并逐渐在犯罪学、矿藏勘探、市场调查、网络信息处理等领域得到了深入研究[1]。

最优搜索理论是关于如何以一种“最佳”的方式寻找某个事先已确定的对象(搜索目标)的理论。最优搜索问题的3个基本要素即目标位置概率分布函数、探测函数、代价函数从模型的角度来讲分别对应了目标初始概率密度、目标探测模型以及搜索资源模型。利用这些模型可以针对静止或运动目标的搜索问题展开研究，例如文献[2]研究了一维随机恒速运动目标的搜索问题，文献[3－4]将静止目标的搜索方法应用到网络信息处理领域，分别研究特定信息搜索和入侵检测问题。

网络用户的浏览行为、通信行为、入侵行为等都受到作息时间、个人行为习惯、入侵方法等的限制，从而在网络数据上反应出一定的规律，例如文献[5]对用户信息查找行为的规律进行了分析，文献[6－7]将行为规律应用到异常检测和入侵检测领域，而以最优搜索为代表的众多优化搜索策略的方法，利用了目标的概率分布，但未对目标的行为规律进行进一步的探讨。

本文从网络数据中分析目标出现的规律，建立其行为规律模型，结合最优搜索理论提出基于行为规律的搜索资源分配算法，解决搜索多长时间和从何时开始搜索的问题，并通过网站关键词的实验证明了算法能够有效提高目标搜索的效率。

2 算法模型

搜索资源主要是指搜索的时间资源，搜索资源分配策略是指根据目标在各搜索区域出现的经验记录，制定出时间资源分配策略，具体包括在各搜索区域的搜索时长和开始搜索的时刻。

新算法的创新在于建立目标行为规律描述模型，并将其引入搜索资源分配策略中，其中目标行为规律是指目标在同一个区域不同时间出现规律的统计。算法结构如图1所示，首先统计目标概率分布，结合最优搜索理论制定各区域搜索时长的分配策略，其中目标概率分布是指目标在各搜索区域出现次数的概率统计;同时统计各区域内目标的行为规律，以获取更多信息为目标检测区域的最佳搜索时刻;最后结合区域搜索时长和最佳搜索时刻，制定目标搜索的时间资源分配策略。

图1 资源分配算法结构Fig.1 Structure of the algorithm

算法用到的符号如下:待搜索区域为 S={S1，S2，…，SN};目标在各区域的出现记录为G={g1，g2，…，gM}，其中 gi= {Si，Ti}，1≤i≤M，Si∈S为第i条记录的出现区域，Ti为第i条记录的出现时刻;算法的结果为 R= {r1，r2，…，rN}，其中 ri={ Si，TLi，TSi}，1≤i≤N，表示了从时间 TSi开始搜索区域Si，共搜索TLi长的时间。

2.1 区域搜索时长分配

按照经典的最优搜索理论，区域搜索时长分配主要包含以下几个步骤。

(1)目标位置概率分布估计

由于目标的行为规律一般以天为单位，因此如果目标出现记录中包含多天的结果，可以进行加权融合。利用 G=g1，g2，…gM}可以统计第i个区域第j天目标出现的总次数Cij，定义规律有效性衰减因子 β=[β1，β2，…，βD]，其中 βk(1≤k≤D)表示第 k天的规律的加权系数，D为规律统计的总天数，则第i个区域的加权次数为C'i=∑Dj=1Cijβj，1≤i≤N，于是可以得到目标在各区域的概率分布估计P=p1，p2，…，pN{}，其中目标在第i个区域的概率为

(2)目标探测函数

用探测函数b(i，t)表示在区域Si上，花费时间t能成功搜索到目标的概率。根据一般经验，若不考虑目标的概率分布，投入到区域Si上的时间t越长，最后能成功找到目标的概率越大，因此可以将探测函数设为如下形式:

其中，1≤i≤N，t＞0，τ 为经验常数。

(3)时长分配策略

设总的时间资源为T，根据目标的概率分布及探测函数，可以得到时间T内发现目标的概率为

其中，f(i)为分配给区域 Si的搜索时长，且

代价函数c(i，t)表示把时间t分配给区域Si的代价，可以简单地令c(i，t)=t，则策略f的总代价为

于是问题转化为有约束的最优化问题:

max P[f]

求解该问题有两个方法:第一种方法是首先忽略约束条件f(i)≥0，1≤i≤N，利用拉格朗日乘数法求得解析解:

然后在解析解的基础上进行结果调整，使得f(i)≥0，1≤i≤N;第二种方法是将该问题转化为有约束最小化问题:

则可以直接利用Matlab的fmincon函数求取数值解。

2.2 最佳搜索时刻检测

目标的活动一般具有规律性，例如以网络活动为例，朝九晚五的上班族一般在上午10点前后会集中处理邮件等日常工作，利用此类规律决定目标搜索的最佳时刻，可以提高搜索到目标的概率。

为了检测最佳搜索时刻，首先建立对目标行为规律的描述:对于区域 Si，以时间分布向量[n't1，n't2，…，n'tH]表示目标的行为规律，其中 n'ti=是多天统计结果按衰减系数的加权，表示第 j天目标在(ti－1，ti]时间段内在该区域出现的次数。

按照上述方法建立每个区域目标行为的时间分布，该分布可能呈现一定的规律性，比如多峰，如图2所示的为双峰现象。

图2 双峰现象及最佳搜索时刻检测示意图Fig.2 The sketch map for double－peak and detection of the optimal search moment

本文主要利用时间分布的多峰现象，将每个区域的搜索时间f(i)分配到各个峰值位置。最佳搜索时刻的最优目标是图2中搜索时间段内曲线覆盖的面积最大，但是通过分析实际数据发现，对应每个区域的行为规律，图2中曲线的形状差异非常大，优化复杂，因此选取了一种相对较优的简化方法，便于在实际工程中使用。以双峰规律为例说明分配方法如下:

(1)利用包络检测的方法，检测最高峰[t1，n1]和次高峰[t2，n2]，其中 t1、t2表示位置，n1、n2表示峰值;

(2)检测t1两侧值为n2的位置，记录时间差t;

(3)若 f(i)≤t，则最佳接入位置为 t1，时长为f(i)，无次佳搜索时刻;否则最佳搜索时刻为t1，时长为，次佳搜索时刻为t2，时长为。

2.3 时间资源分配策略制定

对于双峰规律，得到每个区域的搜索时长和最佳/次佳搜索时刻后，问题转化为根据上述信息在时间轴上完成对搜索时长的分配。本算法采用根据各区域目标出现次数的排序，依次按照最佳/次佳搜索时刻分配区域搜索时刻，流程如图3所示。

沙葱根系发达，耐干旱，能防风固沙，改良土壤，保持水土。早年间，科尔沁沙地里随处可见，但是由于长期过度开垦和放牧，近些年，野生沙葱日渐稀少。

图3 时间资源分配策略制定流程图Fig.3 The flow for time distributing strategy

对于流程的具体说明如下:

(1)统计目标的概率分布，并计算各区域的搜索时长;

(2)对于所有区域，统计每个区域D天的时间分布向量，并加权融合，得到每个区域的时间分布向量;

(3)利用包络检测方法检测时间规律是否具有双峰现象;

(4)对于有双峰现象的区域，完成两段搜索时长的分配，并记录两个峰值为最佳/次佳搜索时刻;

(5)对于没有双峰现象的区域，检测单峰位置，记录为其最佳搜索时刻;

(6)对所有区域，按照目标出现次数进行重要性排序;

(7)按照排序结果，对所有区域，以其最佳/次佳搜索时刻为中心，按照预先分配的时间长度，检测该时间区间是否被占用，若未被占用，确认搜索时刻及时长并更新时间占用情况，否则在最佳/次佳搜索时刻一定范围内移动中心，检测时间是否被占用;若未被占用，确认搜索时刻及时长并更新时间占用情况，否则缩短搜索时长，以最佳/次佳搜索时刻为中心搜索，直至找到合适的搜索时刻;

(8)完成所有区域的初次分配后，检测时间占用情况，对于未被占用的时间段，若时长大于一定门限，根据在步骤7中缩短时长的区域的最佳搜索时刻，选取距离最近的区域填补空白，直至无法填补。

3 试验验证及结果分析

为了验证算法的性能，分两次采集了254个网站(数据集1)以及1 219个网站(数据集2)9天的数据，并按照 gi= Si，Ti{ }(1≤i≤M)的方式记录关键词的每次出现，以此作为试验验证的原始数据。验证过程模拟目标搜索过程，即假设目标为关键词，且关键词按照gi= Si，Ti{ }(1≤i≤M)的方式在网站上出现，搜索目标时仅能搜索到网站实时出现的关键词，不能搜索到已经存在的关键词。验证方法是利用前5天的数据训练目标的概率分布和行为规律，然后利用后4天的数据分别按照制定的策略进行统计，得到每天可以搜索到的关键词次数，并对比不同算法搜索到关键词数量的性能;本算法主要分析一天内的行为规律，因此策略中总的搜索时间资源为1天。

3.1 行为规律分析

图4分别给出数据集1和数据集2中行为规律时间相关性最强的3个网站的相关性变化曲线，其中横坐标代表间隔时间(天)，纵坐标代表相关系数，每个点表示当天数据的时间分布向量与第一天数据的时间分布向量之间的相关系数。

图4 行为规律相关性变化曲线Fig.4 Relativity of behavior rule

由图4可以看出，数据集1中各网站的相关系数随着时间间隔的变大呈现变小的趋势，而数据集2中网站的相关系数保持稳定，没有明显的变小趋势，而且相关性比数据集1中更大。这种现象说明，不同的网站上关键词的行为规律随着时间延续在不断变化，行为规律有一定的时效性;也说明每个网站上不同日期的行为规律具有相关性，虽然相关程度不同，但可以利用前期的数据预测后期数据的行为规律，证明了本算法在原理上是可行的。

3.2 算法有效性对比

表1给出了利用数据集1和数据集2进行验证的结果，其中衰减指数均选择指数衰减。为了体现算法效果，将结果以平均分配方法(各区域分配相同的时长，顺序搜索)为基准进行了归一化，并给出了本算法以及最优搜索方法(只使用最优搜索不利用行为规律)的性能提升对比，性能提升表示相应算法获取的关键词数量与平均方法获取的关键词数量的比值;图5给出了不同算法和数据集的性能提升对比，其中横坐标代表不同日期，纵坐标代表性能提升倍数。

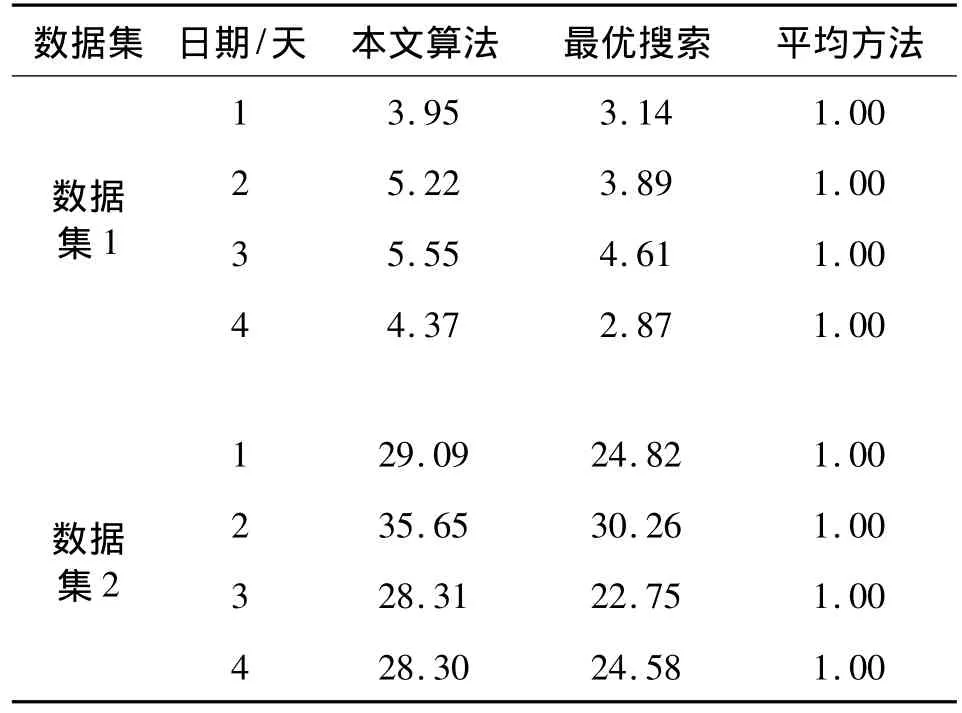
表1 算法性能提升对比表Table1 Comparison of performance advance

图5 性能提升对比图Fig.5 Comparison of performance advance

从表1和图5可以看出，对于数据集1，最优搜索方法的性能是平均算法的3～5倍，本文算法性能是平均算法的4～6倍，本文算法比最优搜索方法性能提升20% ～50%;对于数据集2，最优搜索方法的性能是平均算法的20～30倍，本文算法性能是平均算法的28～35倍，本文算法比最优搜索方法性能提升15%～25%;对照图4可以看出，由于数据集2的行为规律在时间上的相关性更强，因此相对平均算法的性能提升效果更明显。

3.3 训练数据对结果的影响

图6给出了对于数据集1和数据集2，利用5天的数据进行概率分布统计和行为规律统计，且采用不同的衰减因子β时，算法相对于平均分配算法性能提升倍数的结果对比，其中横坐标代表不同日期，纵坐标代表性能提升倍数。无衰减的衰减因子为β=[1，1，1，1，1]，指 数 衰 减 因 子 为 β =[0.018 2，0.049 8，0.135 3，0.367 9，1]，线性衰减因子为 β=[0.2，0.4，0.6，0.8，1]，一天的衰减因子为 β=[0，0，0，0，1]。

由图6可以看出，对于数据集1，采用指数衰减因子时算法性能提升最大，说明了不同日期行为规律相关性随时间降低时，应该采取快速衰减的β，保证行为规律的及时性，而使用1天训练数据的性能提升最差，则是因为由1天数据得到的行为规律具有一定的不稳定性;对于数据集2，使用1天训练数据时性能提升反而要好些，这是由于数据集2的5天训练数据中，行为规律非常稳定，只有第3天的数据偏差较大，因此使用5天训练数据相当于引入了一个噪声，效果反而变差。通过分析可以看出，在算法使用过程中，需要兼顾行为规律的稳定性和及时性，根据行为规律相关性的变化规律采用合理的衰减因子β:时间规律衰减快则选择衰减快的β，时间规律稳定则β的选择对性能影响较小，因此一般情况下，建议选择衰减较快的指数衰减因子。

4 结束语

本文通过分析目标的行为规律，结合最优搜索理论，提出了一种基于行为规律的搜索资源分配算法。利用网站上关键词出现记录进行的模拟搜索试验证明了目标行为规律的存在以及其在稳定性、时效性等方面的特点，实验结果显示，本文的方法相对于平均分配资源能够大幅度提高搜索效率，相对于单独使用最优搜索方法，搜索效率也有显著提高，在对大量信息源进行信息搜索时具有应用价值。另外，在实时处理条件下如何获取各搜索区域完整的历史信息问题未在文中涉及，将是下一步研究的重点。

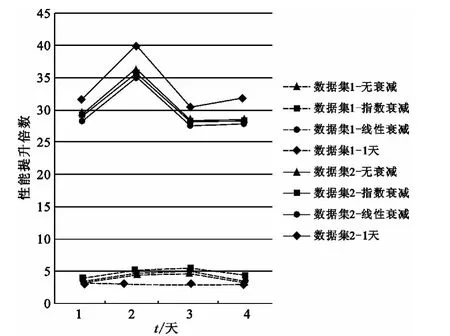
图6 采用不同衰减因子β时性能提升对比图Fig.6 Comparison of performance advance with different β

[1]朱清新.离散和连续空间的最优搜索理论[M].北京:科学出版社，2005.ZHU Qing－xin.The optimal search theory in discrete and continuous space[M].Beijing:Science Press，2005.(in Chinese)

[2]陈建勇，王健.对随机运动目标的一种最优搜索算法[J].海军航空工程学院学报，2012，27(4):456－458.CHEN Jian－yong，WANG Jian.An optimal search algorithm for randomly moving target[J].Journal of Naval Aeronautical Engineering Institute，2012，27(4):456 －458.(in Chinese)

[3]Chu Yanjie，Wei Qiang.A network specific information search system based on mobile agent[C]//Proceedings of 2012 Third Global Congress on Intelligent Systems.Wuhan:IEEE，2012:302－304.

[4]盛志伟，朱清新.最优搜索理论在入侵检测系统中的应用研究[J].计算机应用与软件，2008，25(5):248－250.SHENG Zhi－wei，ZHU Qing－xin.On appling optimal search theory in IDS[J].Computer Applications and Software，2008，25(5):248－250.(in Chinese)

[5]何惠芳.网络环境下用户信息查找行为规律的实证分析[J].情报探索，2008(4):6－8.HE Hui－fang.The analysis of behavior rule of information searching in network[J].Information Research，2008(4):6－8.(in Chinese)

[6]苗强，周兴社.基于行为规律的异常检测技术研究[J].计算机工程与应用，2010，46(15):211－214.MIAO Qiang，ZHOU Xing－she.Research of outlier detection technique based on behavior rule[J].Computer Engineering and Applications，2010，46(15):211－214.(in Chinese)

[7]Mitchell R，ChenI R.Behavior rule based intrusion detection for supporting secure medical cyber physical systems[C]//Proceedings of 2012 International Conference on Computer Communications and Networks.Munich，Germany:IEEE，2012:1－7.