海底观测网电力系统状态估计

冯迎宾，李智刚，王晓辉

（1.中国科学院大学，北京 100049；2.中国科学院沈阳自动化研究所 机器人学国家重点实验室，辽宁 沈阳 110016）

0 引言

海洋蕴藏着丰富的资源[1]，是人类赖以生存的地球系统的重要一环。除了地面、海面与空中的遥测、遥感技术以外，海底观测网已成为地球观测系统的第3个观测平台[2]。与传统的海洋科学研究方法相比，海底观测网的特色和优势在于：第一，观测平台深在海底，可以不受风浪之类的限制，能够连续观测和记录各种突变的信息；第二，能源供应和信息传输网络化，解决了海洋观测中持续电能供给和数据传输的难题，实现了对海洋的长期的、连续的、实时的原位观测[3]。

电能是海底观测网的血液，电能供给的好坏将直接影响海底观测网能否正常运行。海底观测网采取单级负高压直流输电技术进行供电[4]。文献[5-7]分析了海底观测网供电特点，提出了海底观测网2种供电方式恒压并联、恒流串联。

文献[8]论述了海底观测网供电系统恒压并联方式时分支单元的设计方法，实现了海底观测节点的并联连接。分支单元主要功能：在海底观测系统启动过程中，闭合继电器开关，实现整个系统的供电；当海缆发生故障时，断开故障电缆开关，隔离故障，使其他观测节点正常运行。为降低分支单元的复杂性，提高分支单元的可靠性，分支单元不具有通信模块，不能与岸基站直接进行通信，因此岸基站不能获得分支单元的电压值、电流值。为实现对分支单元的电气量检测，需研究一种电力系统状态估计方法估计分支单元的电气量。

文献[9]利用加权最小二乘（WLS）法对分支单元的电压值进行状态估计，其优点是模型简单、计算量小，量测值误差服从正态分布时，其估计结果具有最优一致且无偏等优良统计特性，缺点是抗差能力差，即量测值存在不良数据时，估计结果偏离真值较远。由于WLS法进行状态估计时要求量测量有较高的冗余度，海底观测网的量测量冗余度低，因此降低了WLS法估计结果的精确性。本文针对传感器故障导致量测量误差偏大的问题，提出了抗差能力强的状态估计方法，利用小波变换奇异性检测理论对传感器数据进行分析，识别故障传感器，更新状态估计方程和加权系数，然后利用小波降噪理论降低信号噪声，最后采用WLS法实现无偏估计。

1 小波变换奇异性检测理论

1.1 小波变换

小波变换具有时频域同时局部化性质，即信号在某点处的小波变换在小尺度下完全由该点附近的局部信息所确定，因此它可以有效地确定信号突变点位置。 小波变换定义[10-11]如下。

定义 1 设 f（x）是平方可积函数，ψ（t）是被称为基本小波或母小波的函数，则

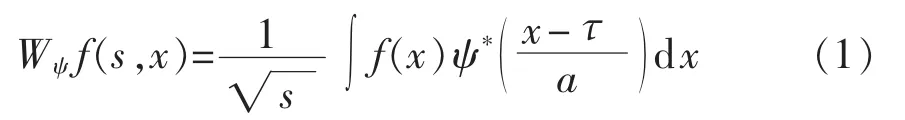
称为f（x）的小波变换。 其中，s为尺度因子；τ 为位移因子，其值可正可负；ψ*（t）为 ψ（t）的共轭函数。

1.2 小波变换模极大值

在小波变换中，小波变换系数 Wψf（s，x0）的值依赖于f（x）在x0处邻域附近的值，并且尺度s越小，邻域区间越小，因此在合适的尺度 s上，Wψf（s，x0）将反映信号在 x0附近的局部信息[12-15]。

定义2在尺度s0下：

a.若对于Wψf（s，x）关于 x 的导数在 x0处等于 0，则称小波变换Wψf（s，x）在（s0，x0）有局部极值；

b.若对x0邻域中的任意点x，都有，并且在左邻域或右邻域满足不等式关系，则称（s0，x0）是小波变换模在尺度s0下的极大点，称是小波变换模在（s0，x0）点的模极大值。

文献[10]已证明，如果信号 f（x）在某区间的小波系数在小尺度上无局部模极大值，则信号f（x）在该区间无奇异性。文献[14]已证明，可以根据故障信号和白噪声的小波变换模极大值在不同尺度上的传递特性的不同，区别小波变换的模极大值是由故障信号引起还是白噪声引起。因此传感器的输出信号f（x）利用小波变换模极大值点的位置来检测信号的奇异点，准确识别出是否传感器出现故障。

如果传感器发生故障，则故障时刻的输出值将发生突变，可以通过小波变换将突变信号放大，从而检测出所对应突变信号的发生时刻。

1.3 传感器故障仿真

传感器故障主要分为偏离故障、冲击干扰、短路故障、开路故障4类。偏离故障由偏置电流或偏置电压变化造成，仿真过程中在传感器输出信号中加上恒定小信号。冲击干扰由电源和地线中随机干扰、电火花放电等造成，仿真过程中在传感器输出信号加上脉冲信号。短路故障由污染引起的线路短接造成，仿真过程中传感器输出信号接近于0。开路故障由信号线断、焊点脱焊等造成，仿真过程中传感器输出信号接近输出最大值。

为检测传感器故障的突变信息，本文选取具有正交、时频紧支撑、高正则性的db3小波，对传感器输出信号进行离散小波分解、重构。图1为传感器输出信号，在50 s时传感器出现偏离故障，在100 s时传感器恢复正常，在150s时传感器受到冲击干扰，在200 s时传感器出现短路故障，在251 s时传感器恢复正常，在351 s时传感器出现开路故障。传感器干扰信号采用方差为0.1的高斯白噪声。

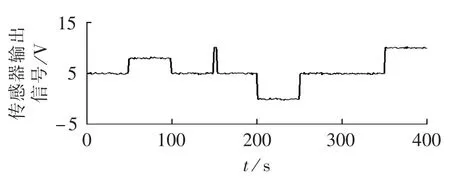
图1 传感器输出信号Fig.1 Output signal of senor

图2显示了传感器输出信号在不同尺度上的分解结果，S1—S3为第1尺度到第3尺度的细节信号。信号的奇异点在细节信号中非常清楚地显示出来。从图2中可以看出，通过小波变换模极大值的位置可以确定奇异点的位置，因此可以检测出传感器故障时刻。

2 状态估计算法

电力系统状态估计的主要功能之一为推算出完整而精确的电力系统各种电气量，即根据周围相邻的量测量推算出没有安装测量装置的各种电气量。本文主要研究利用已知的观测节点的量测量准确地估计未知的分支单元电气量。

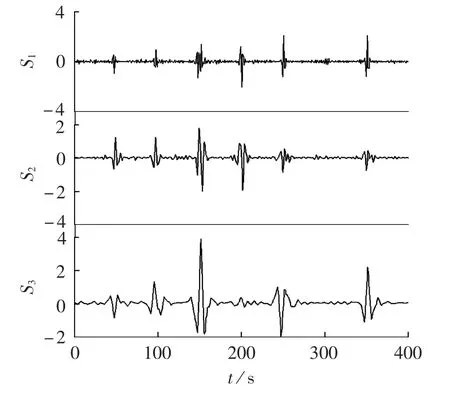
图2 各尺度细节信号Fig.2 Detailed signal for different scales

在给定网络结构、支路参数和量测系统的条件下，电力系统状态估计的线性量测方程为[16-17]：

其中，z为量测向量；x为状态估计向量；H为量测函数矩阵，是只与网络拓扑结构和支路参数相关的常数矩阵；v为量测随机误差向量，假设误差服从均值为0、方差为σ2的正态分布。

采用WLS法进行状态估计，其目标函数为：

其中，W为各量测误差方差的倒数，其元素Wi=1/σ2。由于海底观测网电力系统为线性系统，可以对目标函数J（x）直接求偏导数，当偏导数等于0时，状态量的估计值x为最优。偏导数方程如下：

可得线性状态估计解为：

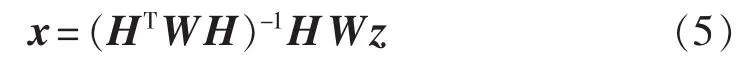
状态估计算法流程图如图3所示。

图3 状态估计算法流程图Fig.3 Flowchart of state estimation algorithm

与文献[9]方法相比，本文算法的特点如下。

a.估计结果不受传感器不良数据影响，具有很强的抗差性。本文算法将小波变换奇异性检测理论应用到状态估计中，在利用WLS法进行状态估计之前已检测出了故障传感器，更新了量测函数矩阵H和量测误差方差阵W，因而估计结果不受不良数据影响，抗差能力强。

b.在具有高斯白噪声的测量误差下，估计结果更加精确。本文算法利用WLS法进行状态估计之前，采用小波降噪方法，对含有高斯白噪声的测量值进行了降噪处理，因此估计结果更加精确，解决了海底观测网量测量冗余度低造成WLS法状态估计结果精度低的问题。

c.算法使用范围广。与传统的状态估计算法相比较，本文算法在测量值冗余度低或者没有冗余度的情况下，估计结果精确度更高，因此使用范围更广泛。

3 海底观测网状态估计

海底观测网电力系统模型如图4所示，主要包括2个岸基站、9个观测节点、11个分支单元。分支单元概念图如图5所示。岸基站和观测节点处的电压值、电流值可测，分支单元之间、分支单元和观测节点之间的阻抗（所研究为直流供电系统，阻抗只考虑电阻的影响，不考虑电抗）已知，估计值为分支单元处的电压值、电流值。

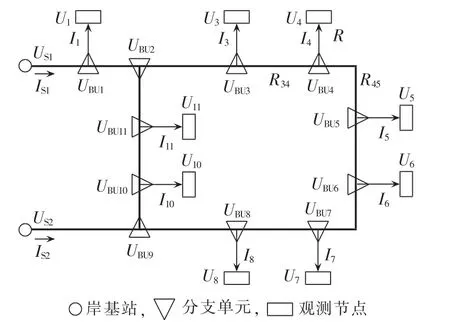
图4 海底观测网电力系统模型Fig.4 Power system model for seafloor observatory network

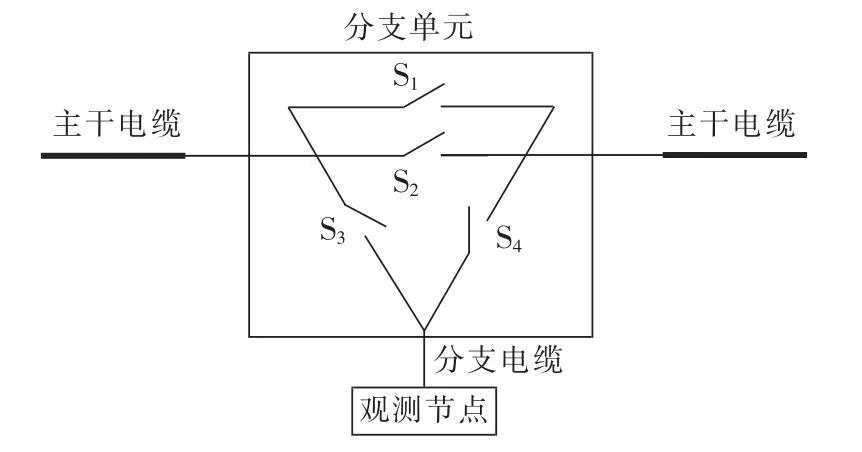
图5 分支单元概念图Fig.5 Conceptional map of branch unit

为实现状态估计，根据海底观测网的电力系统模型，列出已知量与未知量的线性状态方程。以分支单元 3、4、5 为例，U3、U4、U5、I4为观测节点处的量测量，R34、R45、R为分支单元之间、分支单元与观测节点之间的电缆阻抗。根据基尔霍夫电压、电流定律，可写出如下方程：

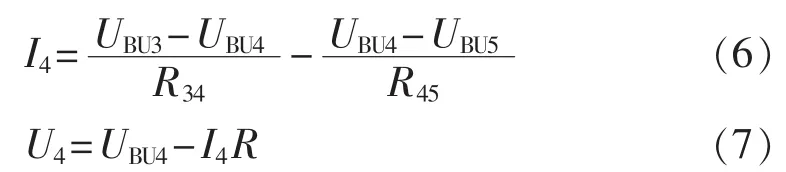
从式（6）、（7）可以看出，观测节点处的量测值可以用分支单元处的电压值和电缆阻抗线性表示。因此观测节点处的量测值构成了式（2）的量测矩阵z，分支单元处的电压值构成了式（2）中状态估计向量x。各传感器误差的方差的倒数构成了W，各单元之间的阻抗构成了量测函数矩阵H。

为了验证本文提出算法的有效性，将该算法应用于海底观测网电力系统模型中，估计分支单元的电压值。其中，量测数据是在测量数据的基础上叠加相应的正态分布随机量测误差而成。在没有传感器故障的情况下，仿真结果如表1所示。从表中可以看出，由于海底观测网电力系统安装的测量装置有限，量测值的冗余度较小，WLS法估计结果不理想，最大估计误差206.6 V，最小估计误差72.1 V。利用本文的算法进行估计，最大估计误差23.9 V，最小估计误差2.3 V。从估计误差的大小可以看出，估计结果得到了有效的改善。

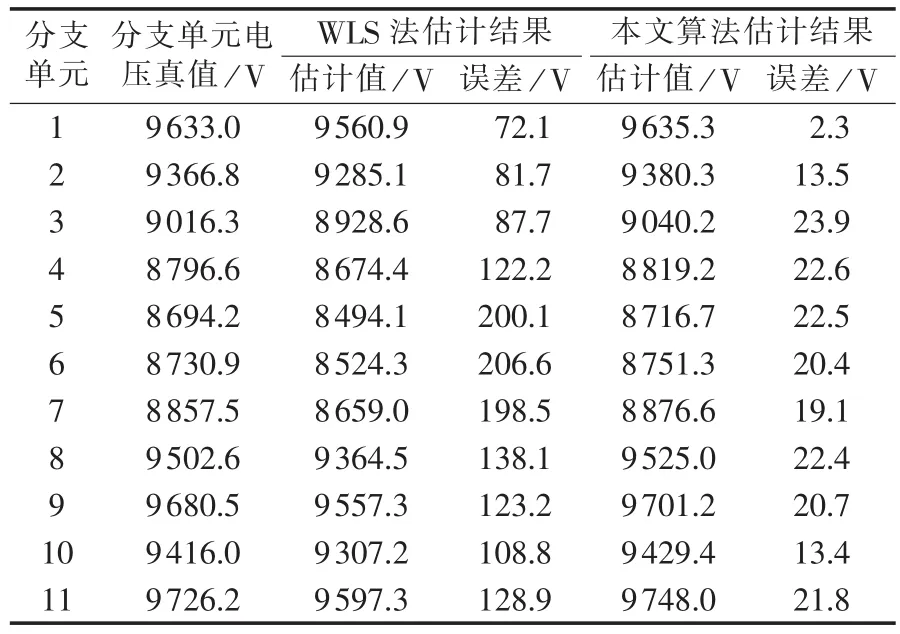
表1 状态估计结果Tab.1 State estimation results

假设分支单元8连接的观测节点处的电流传感器在300s时出现开路故障，输出电流值I8由2.5 A突变为10 A。电流传感器故障对分支单元8处的估计电压UBU8影响最大，图6给出了2种算法对UBU8进行状态估计的估计误差。从图中可以看出：传感器在300 s发生故障，传感器故障前，WLS法估计结果最大误差超过了200 V，而本文算法估计结果最大误差在100 V以内；传感器故障后，WLS法估计结果受到影响，最大估计误差超过了400 V，而本文算法不受故障传感器的影响，最大估计误差保持在100 V以内。

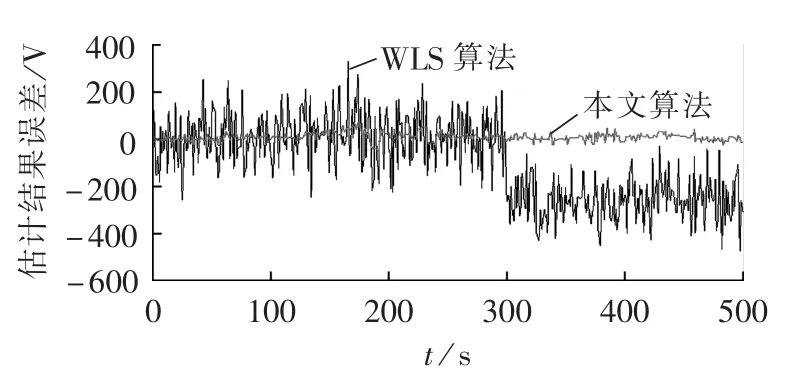
图6 2种算法的状态估计结果误差Fig.6 Comparison of state estimation errors between two methods

4 结论

本文提出了利用小波分析方法和WLS法相结合的电力系统状态估计方法，克服了WLS法状态估计方法抗差能力差的缺点。利用小波变换奇异性检测理论准确地识别出故障传感器，并且更新量测函数矩阵和量测误差方差阵，在WLS法进行状态估计之前，利用小波降噪方法对传感器输出信号进行预处理，进一步提高了状态估计的精度。通过在海底观测网电力系统模型的仿真实验，验证了本文所提出方法的有效性、可行性，具有一定的实用价值。本文所提方法特别适用于量测量冗余度低的电力系统状态估计，对其他电力系统状态估计也具有一定的借鉴意义。