计及风险成本的配电网变电站规划方法
2014-09-27姜小静苏海锋梁志瑞
姜小静,苏海锋,梁志瑞
(华北电力大学 电气与电子工程学院,河北 保定 071003)
0 引言
配电网变电站规划要解决的主要问题就是变电站的选址、定容以及确定各变电站供电范围等问题。变电站的选址定容是一个需要同时考虑各种不确定因素的大规模组合优化问题,它的合理与否直接影响着电网投资、网络构架、运行经济性等一系列问题。因此,配电网变电站的规划是一项非常重要的基础工作[1-3]。
文献[4]首次提出了一种无需事先给定候选变电站的位置和数量的大规模自动寻优的规划方法,此方法的提出极大减少了规划人员的前期工作量,使变电站的规划工作进入了无待选站址的自动寻优阶段。文献[5]在变电站规划的投资和运行费用最低模型的基础上,利用占地费用的经济性指标和站址的地理适宜性指标形成的综合适应度对初始方案进行调整与优化。文献[6]对变电站选址时涉及的不确定性因素众多且很多因素无法量化的问题,提出了采用模糊层次分析法将更多不确定性因素计入规划工作中。而对选址定容工作中的不确定地理因素,文献[7]将土地费用加入目标函数中,建立了基于地理信息的新模型。
上述文献的规划模型均将重心放在了项目的前期投入成本,忽视了后期的运行、维护和报废等诸多过程。而从规划项目长远的经济效益来看,方案的运行成本、维护成本、故障成本和废弃成本的总和会大于它的投资建设成本,这种传统的规划模型存在着重眼前轻长远、重局部轻全局的缺点,难以最大限度地实现变电站规划的经济效益。鉴于以上文献模型的不足之处,为了切实提高变电站规划的投资效益,需要对全寿命周期成本LCC(Life Cycle Cost)管理理论展开全面的研究。文献[8]在LCC的基础上加入地理惩罚因子和隐性成本因子,建立了新建变电站的最小LCC目标函数。文献[9]则分别建立了变电站进线侧、出线侧和变电站站内设备的LCC规划模型。这些研究成果都充分证明了基于LCC的变电站规划模型具有重要的意义。而随着配电网变电站规划风险因素的日益多样化和复杂化,现有的变电站规划研究文献中缺乏从各种不确定风险与经济角度的综合分析,所以考虑各种风险因素的变电站选址定容模型有一定的研究意义。文献[10]采用三角模糊数来描述负荷的不确定性,将它对变电站规划的影响计入到数学模型中。文献[11]中负荷的不确定性、征地费用的不确定性和社会补偿的不确定性分别采用简化的概率密度函数形式来描述,建立了全寿命周期内的期望利润最大的目标函数,但各种不确定风险因素的量化均是在忽略一些实际情况的影响作用下进行的。对此,本文基于LCC理论,从各种不确定风险因素的量化角度出发,对设计、运行、维护到报废的全过程进行风险识别。将负荷的不确定性、电价的不确定性和土地价格的不确定性分别予以具体量化并建立了LCC最小的数学模型,使得方案在满足经济性与可靠性的同时更符合实际情况。
1 变电站规划模型中的不确定风险因素
配电网变电站建设项目风险方面的研究多还处于理论层面,没有太多的参考文献可供研究,所以很有必要对其存在的不确定风险因素进行量化分析。对于配电网变电站规划面临的各种不确定风险,本文从设计、运行、维护和报废的全寿命周期过程进行分析,重点考虑的不确定因素有:负荷的不确定性、电价的不确定性以及土地价格的不确定性。
1.1 负荷的不确定模型
区域负荷的概率分布,既可以反映负荷的不确定性,又可以反映负荷的规律性。所以,采用负荷的概率分布形式来描述负荷的不确定性。
通过该地区某区域一年时间内的历史负荷数据进行概率统计分析发现负荷值为一个服从正态分布的随机变量。因此,规划区域的不确定负荷如式(1)所示:
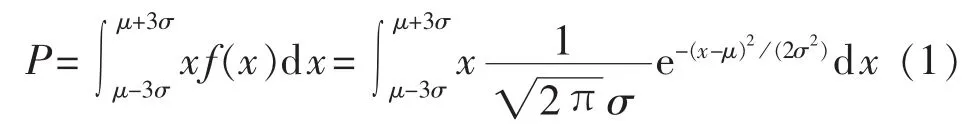
其中,x为规划区域的负荷;f(x)为规划区域负荷的概率密度函数;μ为正态分布的均值;σ2为方差。负荷的正态分布取值位于(μ-3σ,μ+3σ)的概率为99.74%,其值落在(μ-3σ,μ+3σ)内几乎是肯定的,可以满足负荷不确定性的要求。所以区域负荷的不确定结果表示为[Pμ-3σ,Pμ+3σ],即[Pmin,Pmax]。一般又认为区域内的各负荷相互独立,它们的和或差仍服从正态分布[12],所以各负荷点的负荷值也为服从正态分布的随机变量,单点负荷j的不确定区间为
1.2 电价的不确定模型
电力市场中电价的影响因素众多,但对于相同的电力市场很多因素都是相对稳定的。而电力负荷却随着经济发展、生活水平、时间等因素的变化而变化,它和各因素共同影响着电价的变化[13-14]。电力负荷在电价的不确定模型中是一个不容忽视的主要因素,对于负荷有弹性的市场,其电价与负荷需求的反向函数[15]为:
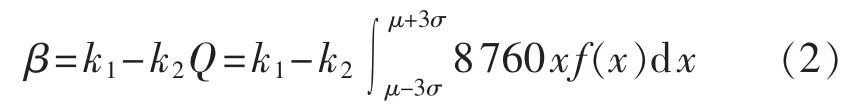
其中,β为电价;Q为规划区域的不确定负荷需求;k1、k2均为不小于 0 的常数;f(x)为规划区域负荷的概率密度函数。
1.3 土地价格的不确定模型
经济的快速发展使人们对电力的需求不断增加,直接导致变电站建设项目的快速增长。然而由土地资源紧缺引发的土地供求矛盾使得变电站的土地费用表现出了很大的不确定性。传统变电站规划中土地费用投资的常规化处理已不符合实际的发展情况。所以根据规划工作的实际情况,本文将变电站土地征用补偿费用的不确定性计算计入到目标函数中。
土地管理法规定的征地补偿标准倍数是一个区间,所以计算得到的补偿价格一般是价格的区间,即最小值和最大值是确定的,而具体的补偿价格受一些不确定因素的影响是不易计算得到的。本文以集对分析方法[16]为理论基础确定的土地补偿价格的表达式为:
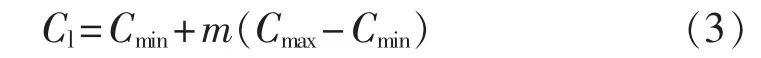
其中,Cmin为土地补偿的最低价格;Cmax为土地补偿的最高价格;m为不确定系数,0≤m≤1。
对于变电站选址用地的价格补偿,考虑影响m取值的不确定因素有:位置因素、当地经济情况、被征地者的生活水平和土地供需情况。其中,位置因素用与城市中心的距离表征;当地经济状况用人均GDP表征;被征地者生活水平用人均收入表征;土地供需情况则通过土地征用者和被征用者的想买卖的对比程度来表征。

其中,ωk为各影响因素的权重;Ek为各因素指标的实际值;Fk为各因素指标的理想值。
2 变电站的规划模型
2.1 变电站容量和数量的配置
由上述负荷的不确定模型得到的规划区域负荷为[Pmin,Pmax],然后对规划区域的负荷性质分析确定负荷的同时率,根据规划区域变压器的容载比范围计算出所需的变压器容量范围。利用不确定负荷的最小值和最大值分别计算的所需变压器的容量范围及最终确定的容量分别如式(5)—(7)所示。
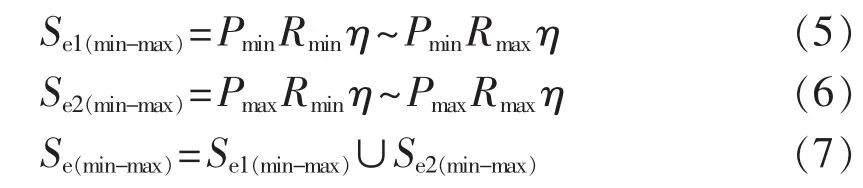
其中,Pmin为不确定负荷的最小值;Pmax为最大值;Rmax为规划电压等级系统的最大容载比;Rmin为最小容载比;η为规划区域负荷的同时率;Semin为所需变电站总容量最小值;Semax为所需变电站总容量最大值。
根据备选变电站的规模容量,利用确定的所需容量范围计算得到需要新建的变电站数量范围如式(8)所示。

其中,S为已有变电站总容量;Sbxmin为新建变电站规模中的最小值;Sbxmax为新建变电站规模中的最大值。
2.2 变电站的LCC规划模型
基于LCC的变电站规划模型的核心内容是对规划变电站的LCC进行分析计算。本文将负荷不确定性、电价不确定性和土地价格不确定性的量化计算分别计入全寿命周期的各个阶段,从而计算规划模型的目标函数值。
配电网变电站的LCC规划模型为:

其中,i=1,2,…,N;LCCHV、LCCLV、LCCS分别为高压侧进线、低压侧配电线路、变电站的LCC;Pj为负荷点j的不确定负荷;Ji为变电站i所带负荷集合;Si为变电站i的容量;e(Si)为变电站i的最大负载率,cosφi为变电站i的功率因数;ULV-ij为变电站i与负荷点j之间的压降值;z为低压侧线路的单位长度电阻;ULV-i为低压侧线路的额定电压;ΔUm为低压侧允许电压偏差的最大值;f(xj)为负荷点j的概率密度函数;N为新建变电站的数量;gij为负荷点j是否由变电站i供电的判别因子,gij=1对应“是”,gij=0对应“否”;lLV-ij为变电站 i到负荷点j的距离;Yi为变电站i的最大供电半径。
2.2.1 变电站高压进线侧LCCHV模型
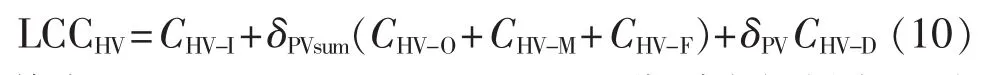
其中,CHV-I、CHV-O、CHV-M、CHV-F、CHV-D分别为规划变电站进线侧的初始投资成本、运行成本、维护成本、故障成本和废弃成本;δPV=1/(1+r)n为折现系数;δPVsum=[(1+r)n-1]/[r(1+r)n]为按年度投资成本的现值和的折算系数;n为寿命周期;r为折现率。考虑到线路的残值较小,本文假设其残值收入和处置成本相互抵消,故 CHV-D=0。
由于考虑了负荷的不确定性和电价的不确定性对各阶段成本量化的影响,因此运行成本CHV-O和故障成本 CHV-F和文献[9]有所不同,分别如式(11)、(12)所示。而初始投资成本CHV-I和维护成本CHV-M的计算方法与文献[9]相同,因此不再赘述。
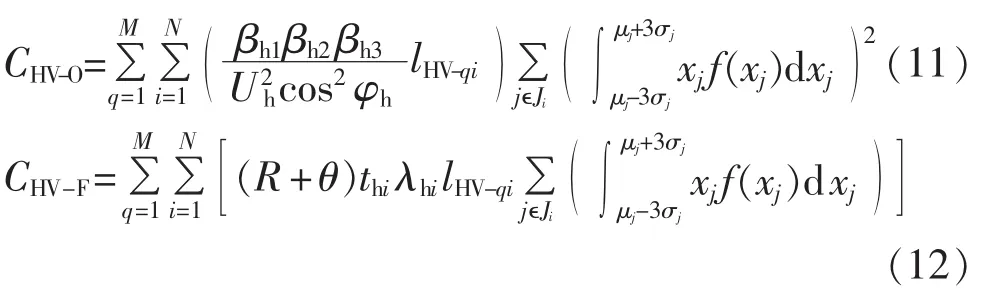
其中,M为高压电源点个数;lHV-qi为高压电源点q到变电站i的距离为不确定电价;βh2为高压侧线路的单位长度电阻;βh3为高压侧线路的年最大损耗小时数;Uh为高压侧的额定电压;φh为高压侧的功率因数角;f(xj)为负荷点 j的概率密度函数;μj+3σj、μj-3σj分别为不确定负荷积分区间的上限值和下限值;R为规划地区的产电比;θ为规划地区的售电利润;thi为变电站i进线侧线路设备故障平均修复时间;λhi为变电站i进线侧线路设备故障率。
低压侧出线LCCLV的构成和计算方法与LCCHV类似,本文不再赘述。
2.2.2 变电站站内LCCS模型

其中,CS-I、CS-O、CS-M、CS-F、CS-D分别为变电站的初始投资成本、运行成本、维护成本、故障成本和废弃成本。
由于本文考虑的土地价格的不确定性、电价的不确定性和负荷的不确定性量化计算分别影响了变电站的初始投资成本CS-I、运行成本CS-O和故障成本CS-F,所以其计算公式分别如式(14)—(16)所示,而维护成本CS-M和废弃成本CS-D的计算方法与文献[9]相同。
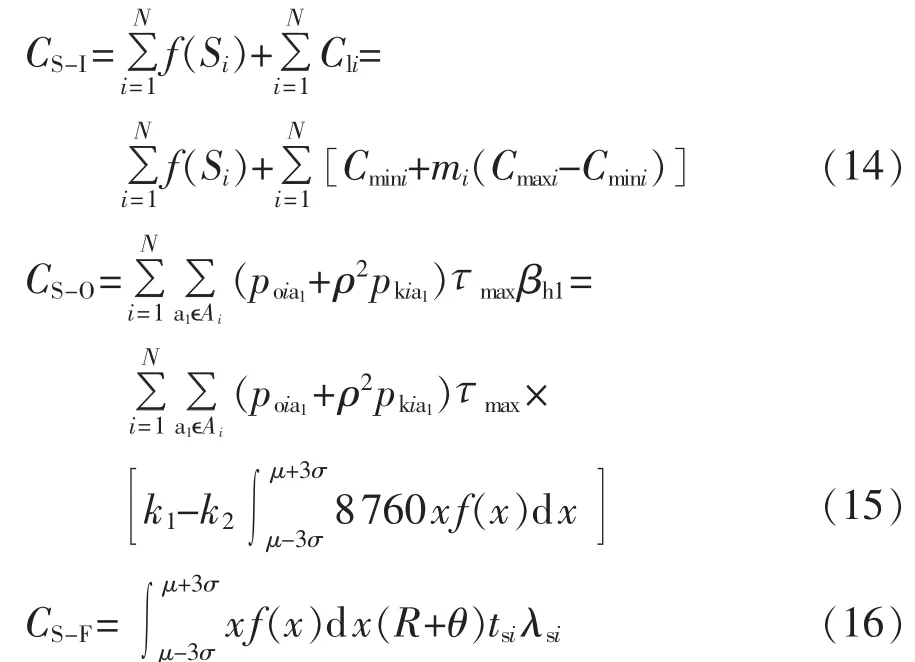
其中,f(Si)包括变电站的设备购置费和安装工程费;Cli为变电站i的土地费用;Cmini为变电站i土地的最低价格;Cmaxi为变电站i土地的最高价格;mi为不确定系数;poia1为变电站i中变压器a1的空载损耗;pkia1为变电站i中变压器a1的负载损耗;ρ为变压器的负载率;τmax为变压器的年最大损耗小时数;Ai为变电站i中主变集合;tsi为变电站i主变设备的故障平均修复时间;λsi为变电站i主变设备故障率。
3 算例
某开发区预测10 a后的负荷位置和预测大小值见表1,该开发区中心位置有一个湖泊,总负荷预测量为128.32 MW。为了满足开发区未来负荷的需求,需新建35 kV变电站,占地面积为1800 m2,新建变电站的规模选择有 3×16 MV·A 和 3×20 MV·A,表 2为候选变压器的参数,2种规模的变电站造价(不包括占地费用)分别为1625.05万元和2486.69万元。规划变电站的容载比要求为1.8~2.2,负荷同时率为0.8。新建变电站的2个上级110 kV电源节点坐标分别为(2.09 km,4.31 km)和(7.34 km,4.35 km),其他参数如表3所示。

表1 各负荷点大小和位置Tab.1 Capacity and position of load nodes
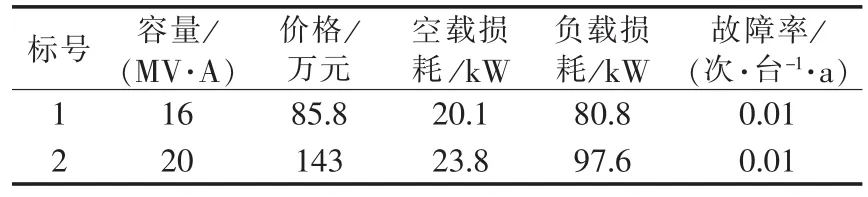
表2 候选变压器参数Tab.2 Parameters of candidate transformer
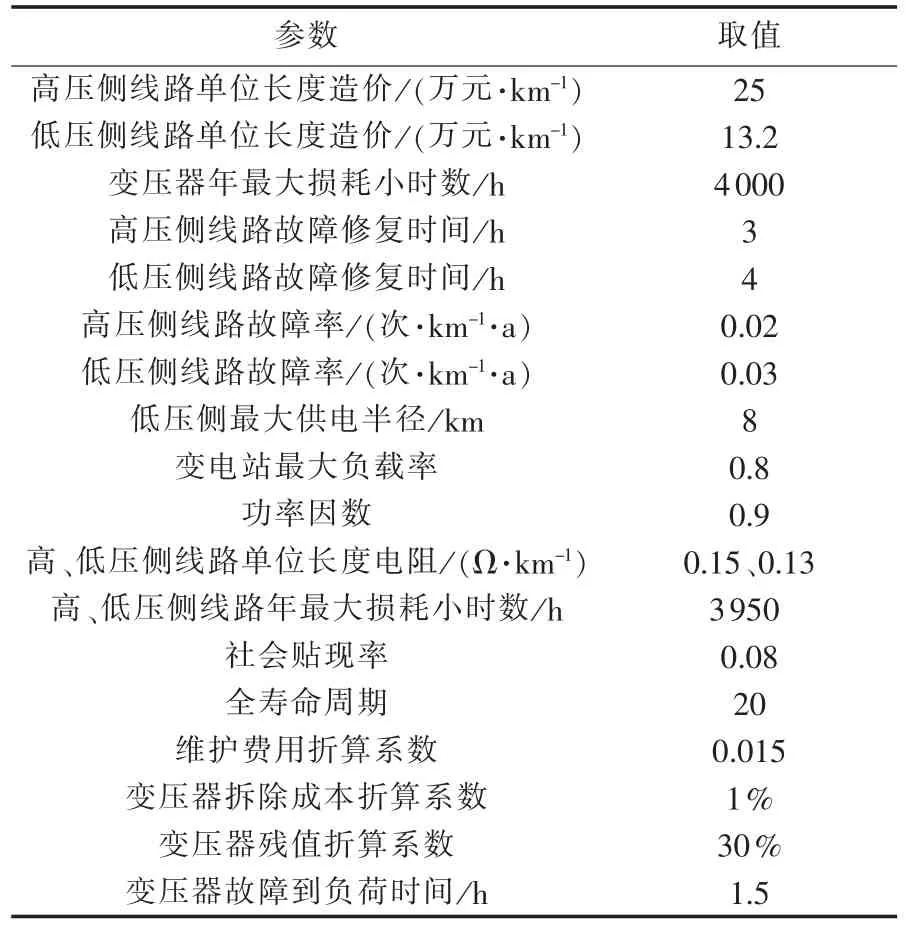
表3 其他参数Tab.3 Other parameters
3.1 算例分析
35 kV变电站的占地面积取常规面积1800 m2。算例中的一些参数取值如下:负荷的不确定性计算中,通过该地区历史负荷数据的最大值和开发区域的负荷预测值之间的比例关系,并利用历史拟合正态分布的均值和方差确定开发区负荷正态分布概率密度函数的均值μ=80.76,方差近似取历史负荷方差σ2=253.351。电价的不确定计算中,利用文献[13]中不同电价与用电量的原始数据线性拟合所确定的系数 k1=0.688,k2=9.05×10-7。
文献[9]中变电站的占地费用计算中,占地1800 m2,合2.7亩,每亩按照购地费45万元来计算,那么可以知道变电站的土地价格为121.5万元。而本文中土地价格的确定首先采用层次分析法分别对规划区中7个不同地块中影响土地价格的各个因素分析得到其权重,然后选择北京市土地价格影响因素的测算值作为理想值分别计算不同的m值。按倍数法评估土地价格的不确定区间的具体标准详见文献[17],则规划区内7个不同地块中的变电站的最高与最低土地价格及最后确定的土地价格如表4所示。

表4 规划区各地块内变电站的土地价格Tab.4 Land price of parcels in planning area
3.2 算例结果
本文规划方法与文献[9]方法的不同规划结果如表 5 所示,表中 CI、CO、CM、CF、CD分别为整个规划方案总的初始投资成本、运行成本、维护成本、故障成本、废弃成本。
表5中为本文规划模型与文献[9]模型的不同规划结果,而本文规划方案的变电站位置坐标、容量如表6所示,其详细布局接线如图1所示。由表5中全寿命周期内不同阶段的计算结果来看,方案的后期运行、维护、故障和报废成本之和远远大于方案的初始投资,所以单纯以初始投资最小为目标函数的传统规划方法的不足之处已显而易见。对比本文规划模型与文献[9]模型的不同规划结果,通过分析可知,由于本文模型中不同变电站位置土地价格的差异,导致本文方案初始投资成本较文献[9]增大,但负荷变化的不确定性及电价的不确定性使方案运行成本相应减少。本文中全寿命周期内各阶段成本的改变使规划方案的LCC较文献[9]中的结果也有所减少,所以计入负荷不确定性、电价不确定性和土地价格不确定性的规划模型使方案的结果更符合实际情况,具有一定的实用价值。

表5 本文方法与文献[9]方法的LCC结果Tab.5 Substation LCC planned by proposed method and by method of literature[9]
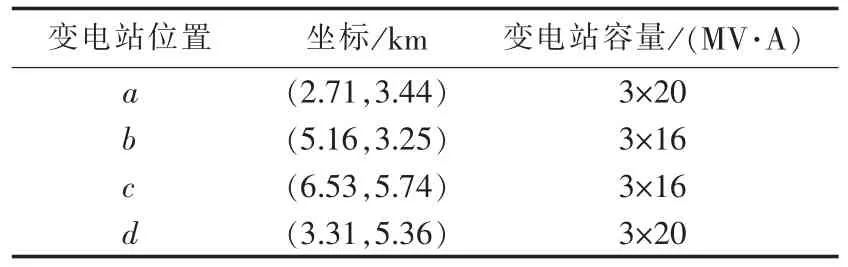
表6 规划结果的变电站位置Tab.6 Substation locations planned by substation planning

图1 最优规划方案示意图Fig.1 Schematic diagram of optimal planning scheme
4 结论
面对配电网变电站规划过程中不确定风险因素的日益增多,本文在LCC理论的基础上,将负荷的不确定性、电价的不确定性和土地价格的不确定性计入了变电站的规划研究中,并通过算例验证了其科学性与实用性。所以,本文建立的最小LCC配电网变电站规划模型的目标函数,在满足可靠性的同时兼顾经济性与实用性。
在考虑各种影响因素作用规划方案时可量化程度的基础上,本文仅将负荷、电价和土地价格的不确定性计入规划方案LCC的数学模型,但配电网变电站规划中的不确定风险因素还有很多,深入研究其他不同影响因素作用的规划方案将会是未来变电站规划的一个重要方向,这对提高LCC的优化管理具有一定的意义。
