基于Gauss-Markov模型的电力系统t型抗差状态估计
2014-09-27颜全椿卫志农徐泰山王胜明孙国强
颜全椿,卫志农,徐泰山,王胜明,孙国强
(1.河海大学 可再生能源发电技术教育部工程研究中心,江苏 南京 210098;2.国网电力科学研究院/南京南瑞集团公司,江苏 南京 210003)
0 引言
自1794年Gauss创立最小二乘LS(Least Square)法以来,特别是Gauss-Markov定理建立后,最小二乘估计一直被作为一个良好的估计方法而被广泛采用。传统的基于最小二乘及由其派生出的快速解耦法状态估计在实际电网已有多年的运行经验,该方法是对服从高斯分布样本的最优估计,具有模型简单、计算量小、收敛速度快等优点[1-2]。然而,实际量测系统中往往存在误差较大的不良数据,而这些不良数据并不服从高斯分布,若不能将这些不良数据剔除,将严重影响状态估计结果的精度。因此,研究如何尽可能地降低不良数据对电力系统状态估计的影响具有重要意义[3]。
针对该问题,国内外学者的研究主要侧重2个方面:一方面是在最小二乘估计的基础上,嵌入一个含不良数据辨识的模块[4-6];另一方面则是以M估计为代表的抗差状态估计[7-12]。对于前一方面研究,目前应用较广泛的是估计辨识法,即首先找出残差较大的量测作为不良数据,用估计值直接修正原来的状态估计,修正后的状态估计恰恰是不良数据的最优估计。该方法无需重新进行状态估计,实时性好,但存在仅可辨识多个弱相关的不良数据、较难处理含多个强相关的不良数据的不足。对于后一方面研究,M估计的抗差性和效率取决于状态量初值的可靠性、等价权函数及其临界值的合理性。电力系统状态估计中使用比较广泛的权函数有Huber权函数、Hampel权函数、Turkey权函数和含有相关量测的IGGШ权函数等。不同等价权函数的选取相当于建立了不同的误差分布模型。统计界近年来提出并有较深入理论研究支撑的t型估计,以t分布对量测误差建模,属于带有刻度参数的M估计[13-15]。当t分布取较大的自由度时,趋于高斯分布,对应最小二乘估计,在量测误差为高斯分布时具有较高的效率;当取较小的自由度时,为柯西分布,相应的估计具有很好的抗差性。恰当地选取自由度,可以使t型估计兼顾状态估计的抗差性和效率。
本文在前人工作基础上,将t型估计引入电力系统状态估计中,针对t型估计求解较繁琐的特点,提出近似模型,并以零注入节点方程为等式约束。随后,利用牛顿法进行求解,结合一个简单的电力系统算例分析该方法在实际应用中可能存在的局部最优点问题,通过分步调整自由度保证取得全局最优解。最后,借助IEEE标准系统和某实际电网测试该方法的有效性,结果表明,与含不良数据辨识功能加权最小二乘(WLS)估计(简称 WLS+BD)和二次-常数QC(Quadratic-Constant)估计进行比较,本文方法处理不良数据能力更强。
1 t型估计模型及其求解
1.1 电力系统t型估计模型
在给定网络结线、支路参数和量测系统的条件下,电力系统的量测方程为[1]:

其中,x为n×1维状态变量,包括除平衡节点外的所有节点电压幅值和相角;zi、hi、ri分别为 m× 1 维量测向量、量测函数向量和残差向量的第i个分量;m、n分别为量测量及状态量的个数。
考虑量测误差的Gauss-Markov模型为:

其中,σ0为未知的单位权方差因子;E(r)、D(r)分别为量测残差的均值和方差;R为量测权重对角矩阵。
对于式(2),定义t型抗差状态估计为如下的最优化问题[13]:
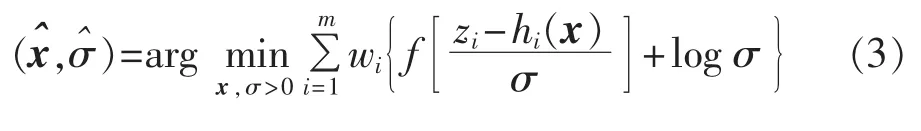
由于在实际运行中,系统必须满足零注入节点的等式约束,考虑这些约束则式(3)可写为:
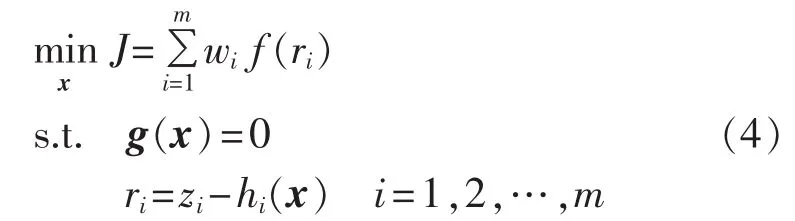
其中,g(x)为潮流约束及零注入节点功率量测的等式约束。
1.2 求解
利用内点罚函数法对式(4)进行处理,则式(4)可转化为以下无约束的优化问题[9]:
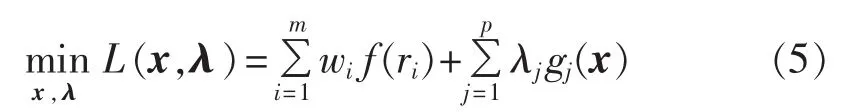
其中,L(x,λ)为拉格朗日函数;λ为p维拉格朗日乘子向量;gj(x)表示第 j个等式约束。
式(5)中 L(x,λ)的一阶最优条件为:
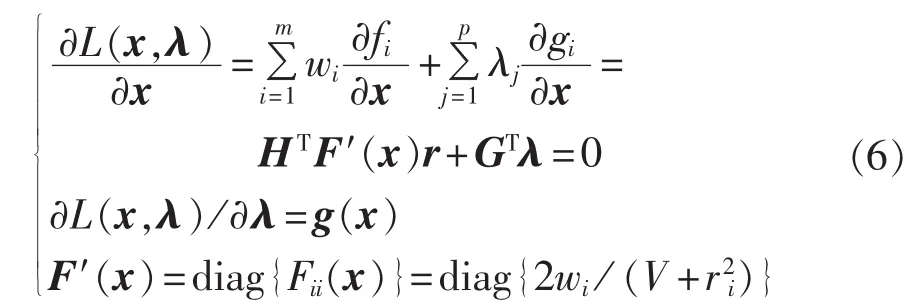
其中,H为h(x)对x的雅可比矩阵;G为零注入节点等式约束g(x)对x的雅可比矩阵。
通过牛顿法求解式(6)的非线性方程,对式(6)求偏导可得增广拉格朗日函数L(x,λ)的海森矩阵:
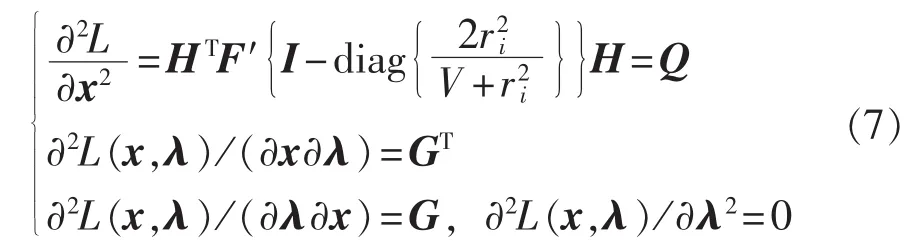
式中,∂2L/∂x2部分忽略了二阶项,在形式上与传统WLS类似,具有较好的兼容性。
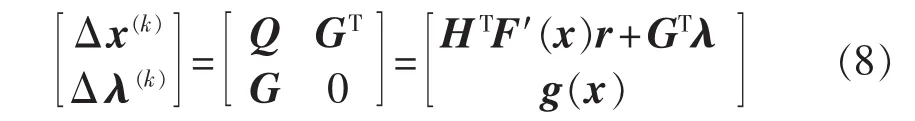
令 x(k+1)=x(k)+Δ x(k+1),λ(k+1)=λ(k)+Δλ(k+1),即可对式(4)的t型抗差估计模型进行求解。
因此,可得如下修正公式:
2 局部最优解情况分析
从数学上看,t型估计是一个典型的非线性优化问题,可能存在局部最优解。以2节点系统为例进行测试,该系统的潮流分布及网络参数参见文献[9]。由于2节点系统平衡节点B1的电压为1.05∠0°p.u.,不参与迭代,因此优化变量仅有节点B2的电压幅值与相角。
分别取V=0.01和V=1,t型估计目标函数随着节点B2电压幅值和相角变化的曲面如图1、2所示,图中电压幅值为标幺值,后同。为了便于观察,将目标函数J(x)符号取反,图3、4给出了相应的等值线。
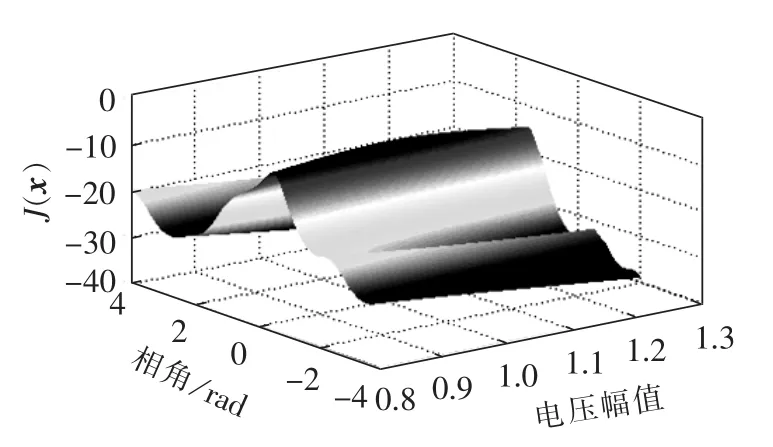
图1 V=0.01时t型估计目标函数J(x)的变化曲面Fig.1 Curved surface of objective function J(x)of t-type estimation when V is 0.01
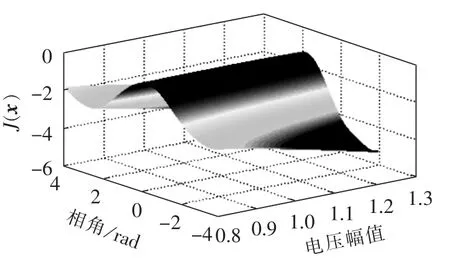
图2 V=1时t型估计目标函数J(x)的变化曲面Fig.2 Curved surface of objective function J(x) of t-type estimation when V is 1
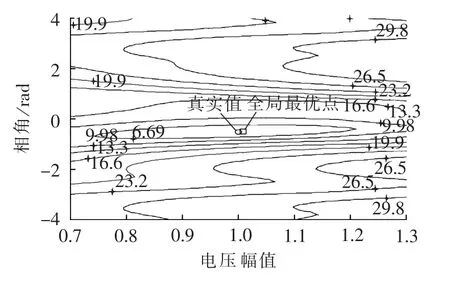
图3 V=0.01时2节点系统目标函数等值线图Fig.3 Contour map of objective function of 2-bus system when V is 0.01
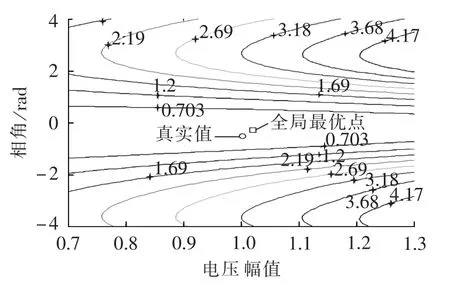
图4 V=1时2节点系统目标函数等值线图Fig.4 Contour map of objective function of 2-bus system when V is 1
由图1及图3可知,V=0.01时,全局最优点为1.005∠-29.22°p.u.,与真实值 1.002∠-30°p.u.误差较小,但此时目标函数出现多个局部最优点。图2中,V=1,此时局部最优点消失了,但是全局最优点为1.020∠-16.62°p.u.,偏离了真实值。进一步,本文对取不同自由度时全局最优点的影响进行分析,结果如表1所示。由表可知,自由度V取值越小,估计结果的精度越高,全局最优点与真实值越接近。
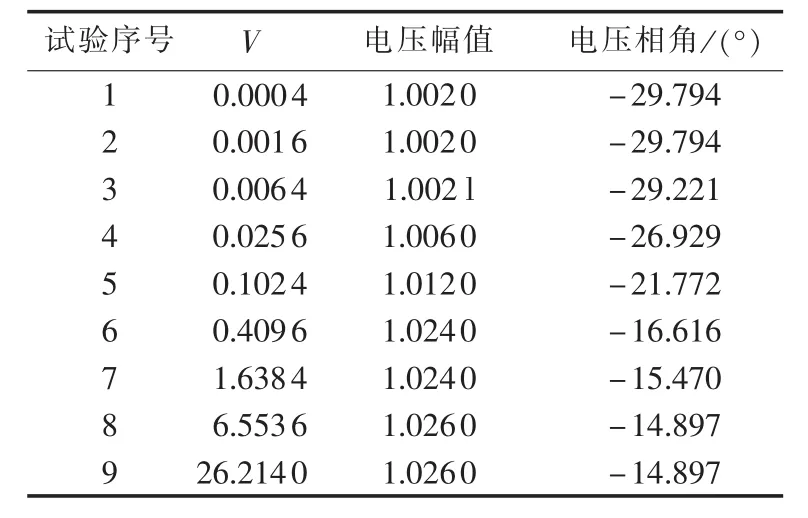
表1 自由度V对全局最优解的影响Tab.1 Impact of V on globally optimal solution
实际上,V值的改变与文献[9]中的Parzen窗宽度类似,在数学上其作用是等价的。由图4可知,局部最优点与全局最优点距离较远,当节点电压在真实值的较大邻近区域内取初值时,不会陷入局部最优点。因此,如何确定初值是本文算法的关键。对于工程应用,可将前一断面的状态估计结果作为后一断面状态估计的初值,根据电力系统运行状态一般变化较平缓的特点,能有效减少迭代次数,从而提高程序收敛速度。同时,文献[9]采用逐步调整Parzen窗宽的策略进行多次迭代求解,能有效克服局部最优解问题,但存在收敛速度较慢的不足。本文对自由度进行动态设置[7]:
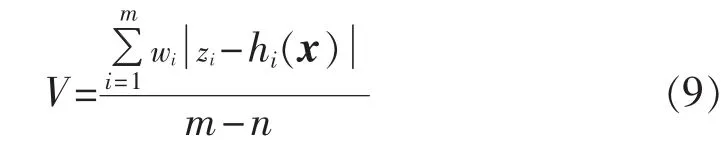
由式(9)可知,自由度的确定与量测系统的残差大小有关。t型估计的计算流程如图5所示。
3 方法特点
与以往的状态估计方法相比,本文方法特点如下。
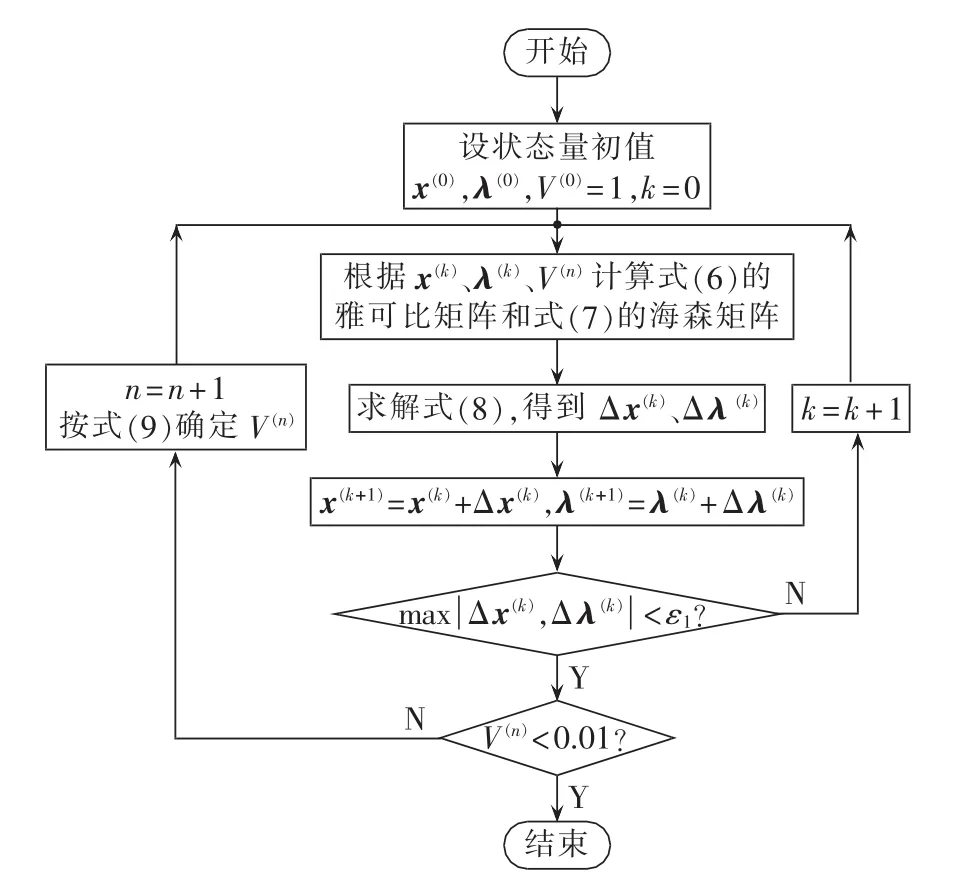
图5 自适应t型状态估计流程图Fig.5 Flowchart of adaptive t-type estimation
a.传统WLS状态估计方法结果易受不良数据影响,本文方法以量测残差对数函数值作为目标函数,能够有效减小不良数据对状态估计结果的影响,抗差性强,估计结果合理性好。
c.该方法在循环迭代求解过程中通过对自由度动态调整,可有效克服局部最优解问题[9]。
4 算例分析
为了验证本文方法的有效性,在Visual C++平台上编制了自适应t型抗差估计。对IEEE标准系统和某实际输电网的数据进行试验,通过将潮流结果加2%高斯随机误差获得量测生数据,通过对生数据置0的方式得到试验用的不良数据。
4.1 抗差性测试
4.1.1 4节点系统
由残差方程知,某量测上出现不良数据时,对自身及其他量测的残差均产生影响。由于量测误差的不确定性,反映在残差上的情形也非常复杂,本文仅考虑2个量测间的相关性,r与量测误差v存在以下关系:
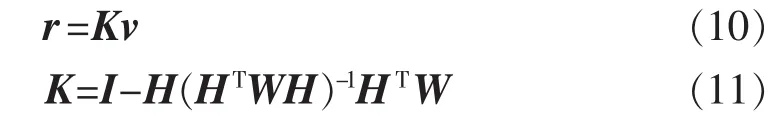
其中,K为残差灵敏度矩阵。
对于t型估计,若量测i的残差较大,则对角元素 Fii(x)=2wi/(V+r2i)≈0,即对该量测降权处理,由此可以得出,t型估计模型中抑制不良数据的影响是可能的。
以下针对4节点系统[16]进行测试,分析含强相关不良数据时状态估计结果的准确性。该系统的结构、量测分布和节点电压真值如图6所示。
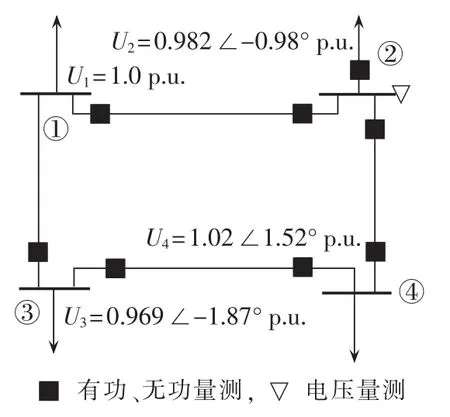
图6 4节点系统结构图Fig.6 Structure of 4-bus system
在给定的量测系统和网络结构下,找出具有强相关性的量测对(CM),并分析不良数据对该量测估计值的影响。相关性分析可通过统计K中的相关系数,量测i与量测j之间的相关度指标[12]为:
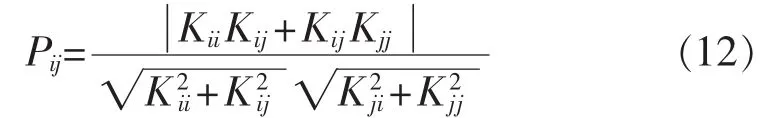
其中,Kij为K的第i行第j列元素值。
当相关度指标满足0.752 1<Pij<0.9498时,为强相关量测对。该系统含4组强相关量测,各估计方法的强相关量测指标见表2。这4组量测对于WLS估计均为强相关量测,而采用t型估计后,相关度指标显著减小。

表2 4节点系统强相关量测指标Tab.2 Strong correlation measurement index of 4-bus system
为进一步测试不同方法对强相关量测不良数据的估计精度,对上述4组强相关量测添加不良数据,不同方法的估计结果见表3,表中数据均为标幺值。
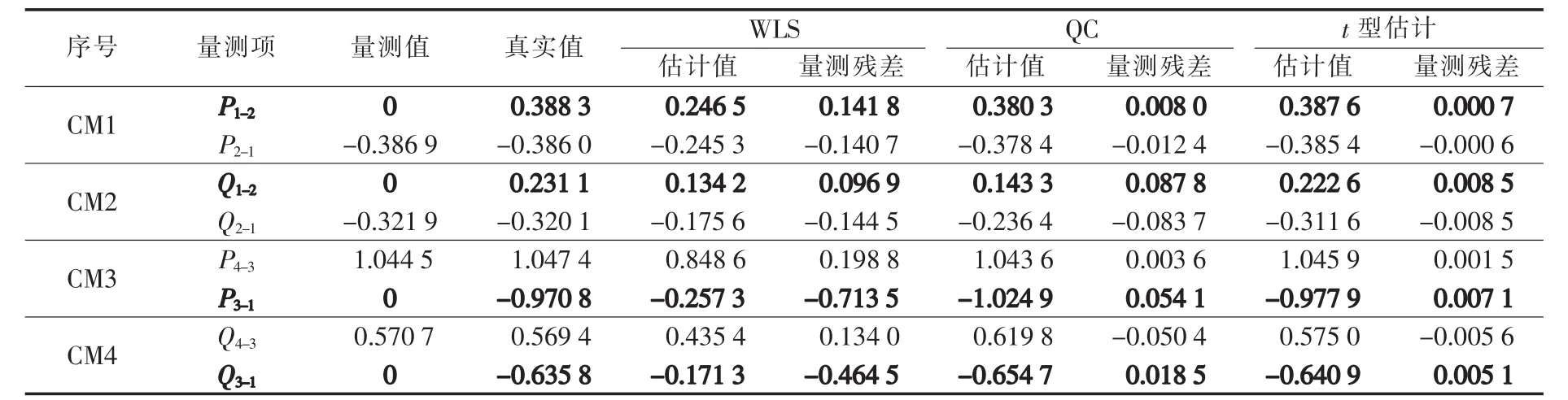
表3 4节点系统强相关量测不同方法的估计结果比较Tab.3 Comparison of estimation results among different strong correlation measurement methods of 4-bus system
以支路1-2有功功率P1-2为例说明不同方法的抗差性能,由表3可知,该量测的真值为0.3883 p.u.,WLS估计结果为 0.2465 p.u.,残差为0.1418 p.u.,而 t型估计值为0.3876 p.u.,残差仅为0.0007 p.u.,很好地辨识出了不良数据。此外,对于该支路P2-1功率量测,t型估计的误差也仅为-0.0006 p.u.,表明t型估计成功辨识出了该组强相关不良数据。
4.1.2 IEEE 57节点系统
采用以下指标衡量估计的状态变量(除平衡节点外其余节点的电压幅值和相角)的准确性[10]:
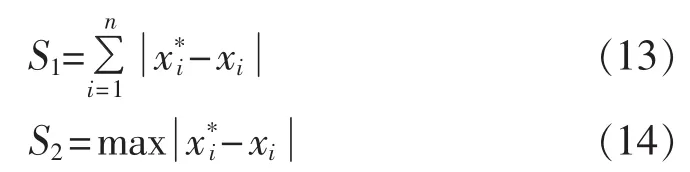
其中,x*i为第i个状态变量的估计值;xi为状态变量的真实值。
表4给出了57节点系统的试验结果,该系统含421个量测。由表4可知,本文方法随着不良数据比例的增加,S1指标和S2指标变化较小,表明本文方法不易受不良数据的影响。
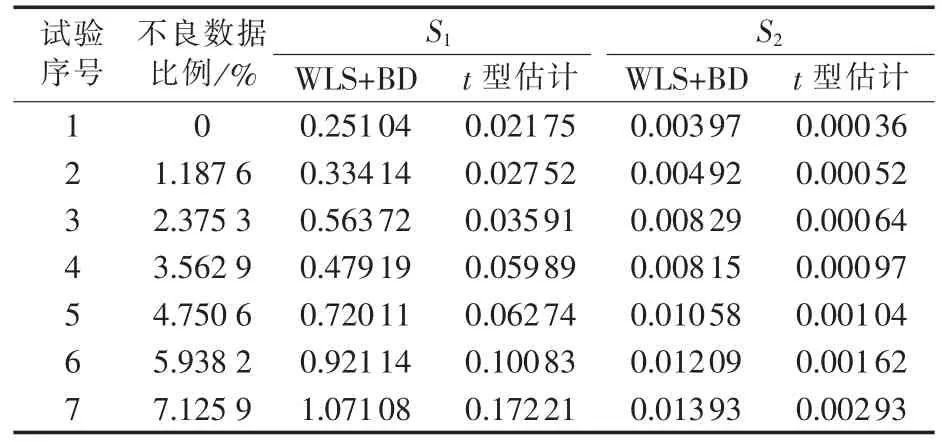
表4 57节点系统试验结果Tab.4 Test results of 57-bus system
4.1.3 某实际省网
为了验证本文方法在实际电网中的性能,对某输电网进行测试,该系统含1 119条母线、1 992条线路(简称省网A)。由于实际系统中量测的真实值无法得到,本文对不同状态估计结果进行合格率评估[10]。表5、6给出了各类型量测的考核基准值与合格门槛值,不同方法的状态估计合格率如表7所示。
由表7可知,6个时间断面中,WLS+BD估计的合格率最低为93.54%,而本文方法的合格率最低为96.24%,相比WLS+BD提高了2.70%。QC估计最低合格率为95.06%,较WLS+BD有一定程度的提高,但仍低于t估计。试验结果表明本文方法具有较强的抗差性。
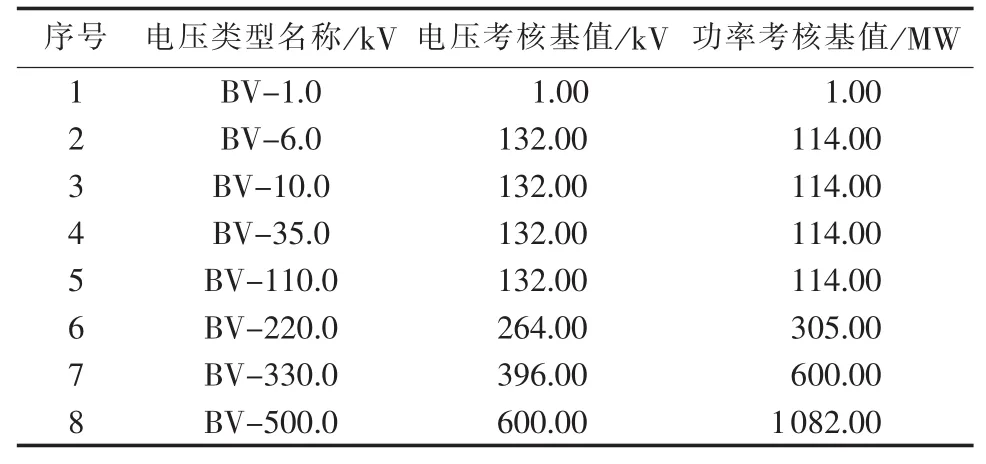
表5 状态估计合格评估基准值Tab.5 Benchmark of state estimation conformity assessment
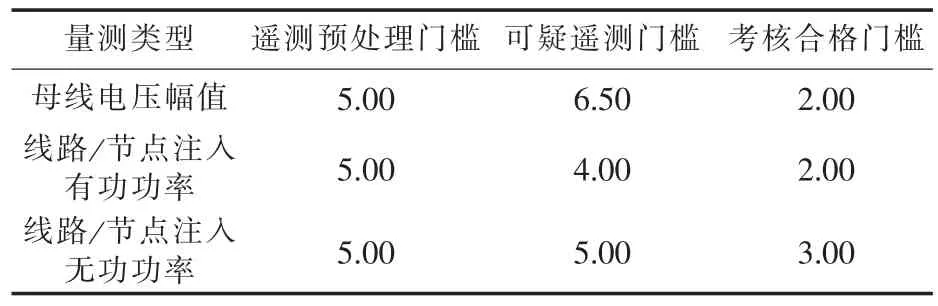
表6 状态估计合格评估门槛值Tab.6 Threshold of state estimation conformity assessment
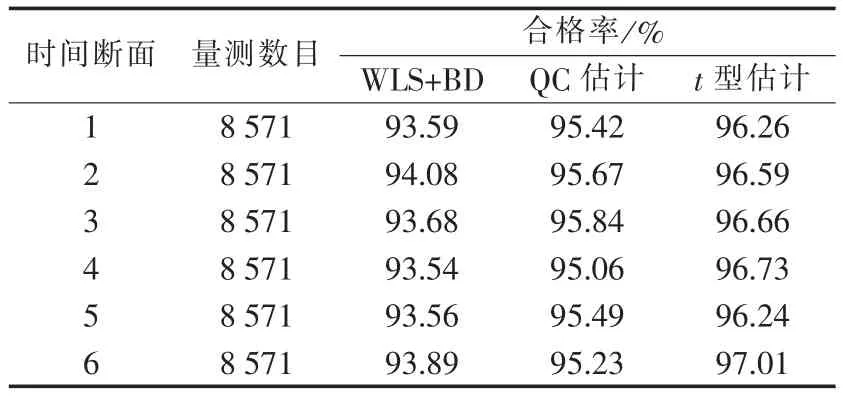
表7 某实际输电网试验结果Tab.7 Test results of a practical transmission network
4.2 自由度对估计结果的影响测试
第2节讨论了本文方法的局部最优解问题,提出了动态调整自由度的策略[7,9],并对 2节点系统进行了分析,由试验结果可知自由度的选择及初值的选取方法将决定算法的最终结果。本文对IEEE 57节点系统进一步分析,采用定V方式(以WLS状态估计结果作为系统状态量初值)进行t型状态估计计算。同时,为了验证本文动态调整自由度V方式的有效性,表8给出了上述不同自由度下状态估计的结果比较。
由表8可知,随着自由度V的减小,S1及S2指标逐渐减小,即较小的自由度具有更强的抗差能力。当自由度V=1时,S1指标为0.27415,平均误差为0.00243,最大误差为0.00481。在试验中发现,本文方法在第1次迭代后利用式(9)计算得到V=0.0129,继续进行迭代计算,经过5次迭代收敛后V=0.00268,满足收敛条件。最终t型估计结果S1指标进一步减小至0.01638,仅为第1次迭代时的5.975%。同时,与定V方式比较可知,该方法并未陷入局部最优解。在计算效率上,定V方式经4次迭代总时间为26.014 ms,而本文仅为11.892 ms,表明本文混合策略在保证求解精度的前提下,显著提高了收敛速率。
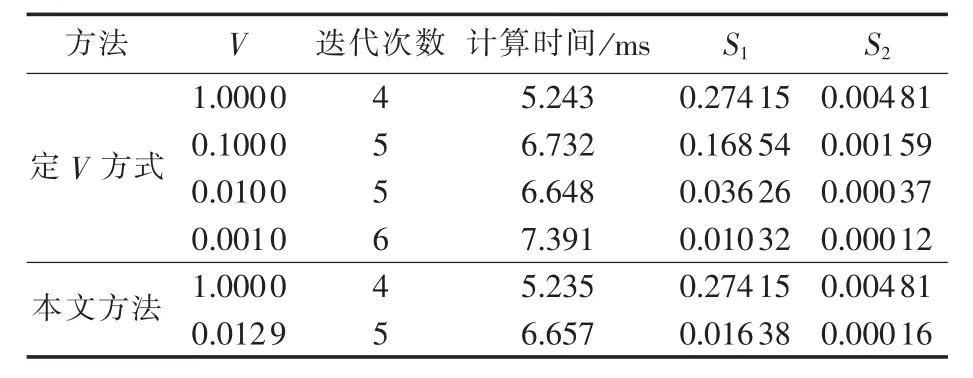
表8 不同V值的t型估计结果Tab.8 Results of t-type estimation for different V values
为了进一步验证本文动态调整自由度策略在实际省网中的有效性,图7给出省网A的120个量测断面状态估计时间。由图7可知,采用文献[9]的定V方式时,由于每次状态估计需4次循环迭代求解,平均计算时间为0.4447 s,而采用本文方法后,平均计算时间为0.367 2 s,相比文献[9]可减少17.43%。同时,本文方法估计结果具有与定V方式同样的精度,这也进一步说明了本文动态调整自由度策略在保持状态估计求解精度的前提下,可有效减少t型估计的计算时间。实际上,目前抗差估计的计算量往往较大,这也是制约其在实际中进一步应用的原因[9]。对于该省网,实际现场采用的WLS估计平均计算时间为0.1765 s,仅为本文方法的48.07%,因此,如何进一步提高计算速度是今后一个重要的研究内容。
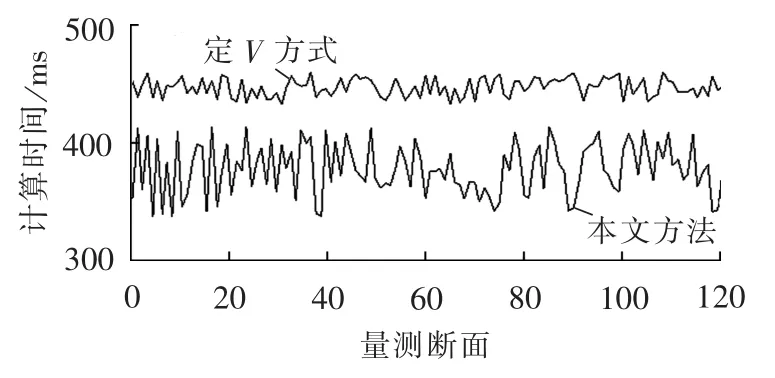
图7 某实际省网t型抗差状态估计计算时间比较Fig.7 Calculation time of t-type state estimation for a practical provincial network
5 结论
本文基于t型估计,建立了适用于电力系统状态估计的简化模型,利用其目标函数连续可微的特点给出类牛顿法的求解方法。该方法具有如下特点。
a.以t型分布对误差建模,当取较小自由度时,具有良好的抗差性能,有效排除不良数据对状态估计结果的影响。
b.提出自适应动态调整自由度的策略,兼顾了t型估计的效率和抗差性,满足工程要求。
c.作为一种新的抗差估计,t型估计有很好的理论基础,将t型估计引入电力系统状态估计中,能够丰富和发展抗差状态估计的理论和方法。与传统WLS估计相比,本文方法计算量仍然较大。
