电力系统故障录波数据实用压缩方法

黄 纯，杨帅雄，，梁勇超，刘 琨，文 超，，郭振华

（1.湖南大学 电气与信息工程学院，湖南 长沙 410082；2.湖南省电力公司检修公司，湖南 长沙 410002）

0 引言

电力网络发生故障时，故障录波装置会动态记录系统电流、电压及其导出量等，以检测继电保护与安全自动装置的动作行为，分析系统暂（动）态过程中各电气量的变化规律，校核电力系统计算程序及模型参数的正确性。

由于故障暂态信号是一种非平稳信号，覆盖的频谱较宽，因此要求录波装置的采样率较高，通常为kHz级，从而得到了海量的故障录波数据，使得故障信号的存储和实时传输面临困难[1]。录波数据压缩技术可以解决这一问题。

小波变换是目前数据压缩的最常用方法。文献[2-5]分别利用多小波、双正交小波、小波包及自适应小波变换压缩故障录波文件；文献[6]提出了小波最优分解层数的确定公式；文献[7]讨论和比较了小波变换的不同预处理方法对数据压缩的影响。此外，LZW编码、图像处理等技术也被应用于电力记 录数据的压缩[8-9]。

本文立足于整体录波文件，根据故障录波数据的特点，提出了分通道分时段压缩方案，即针对某一通道某一时段的录波数据，以快速傅里叶变换（FFT）重构误差为依据，判定使用FFT压缩或者小波压缩。通过MATLAB仿真和华中电网实际故障录波数据，验证了本方案的可行性及优越性。

1 故障录波数据特点

根据IEEE的COMTRADE标准，一个完整的录波文件通常由3个文件构成，即头文件、配置文件和数据文件。其中数据文件包含实际录波数据，该文件按采样时间点顺序进行记录。采样时间点数取决于记录时间的长短，每一采样时间点采集的数据个数取决于录波装置。每个数据采样记录格式如图1所示，其中n为采样编号（4字节）；timestamp为采样时标（4字节）；A1、…、Ak为模拟通道采样数据，每个通道数据大小为2字节；D1、…、Dm为状态通道采样数据，以每16通道2字节（16位）为单位，即16个状态通道为一组连续显示。

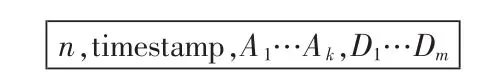
图1 数据采样记录格式Fig.1 Format of data sampling record

按照我国 DL/T553—94《220～500 kV 电力系统故障动态记录技术准则》[10]要求，模拟量信号需按故障发展的顺序分A、B、C、D、E5个时段进行采样，其中，A时段为系统大扰动开始（t=0）之前的状态数据，输出原始记录波形及分析值；B时段为系统在大扰动初期的状态数据；C时段为系统在大扰动中期的状态数据；D时段为系统动态过程数据；E时段为系统长过程的动态数据，直到故障或振荡结束。

故障录波是从系统某处故障前一段特定时间开始的，而其他线路是正常运行的，因此大多数模拟通道数据不受故障影响或影响较小，在整个记录时段内，近似呈稳态周期性变化，信号以基波分量为主，可能还包含高次谐波；大多数开关量（状态通道数据）在录波过程中不会发生变化，因而包含大量的冗余信息。

2 数据压缩方案

根据录波数据的上述特点，对于模拟通道数据，用FFT算法和小波变换分别对正常数据和故障数据进行压缩；对于状态通道数据，若其在录波时段发生变化，则记录其变化起始点和结束点的时标以及各变化段的状态值，否则只需记录原始状态值。

2.1 FFT压缩方法

对模拟通道数据进行FFT计算，在某个给定的错误容限下，把小于相应阈值的FFT系数置零，减少需要传输的系数，从而实现压缩。对于离散的周期信号，FFT压缩效果非常好。

2.2 小波变换压缩方法

小波变换压缩的基本目标是使信号在时间-频率域的分解系数所占的存储空间尽可能小，同时还要保证压缩后的系数能精确地反映原始信号所携带的信息。在实现的过程中，信号可以用近似系数加部分的细节系数来表示，以达到用更少的空间来存储小波系数并尽量保证重建质量的目的。压缩过程可以分为如下3个步骤：

a.对原信号进行小波分解，得到分解系数；

b.对小波域中的系数进行处理，去除信号中的冗余（可以指定压缩的一些参数来获得需要的压缩比、误差等性能指标）；

c.利用处理后的系数，重建压缩后的信号。

2.3 录波数据压缩方案

以输电线路故障录波为例，其录波数据的压缩流程示意图如图2所示。录波通道数据为某一线路的电气量，包含5段不同采样率的采样数据，从A段开始逐一进行FFT压缩，以重构信号与原信号的误差作为压缩成功与否的判断准则：若重构误差大于阈值，则进行小波变换压缩，然后读取下一段的数据；否则直接进入下一段数据的读取。如果本通道数据已经压缩完毕，则重新开始下一通道数据的压缩流程。

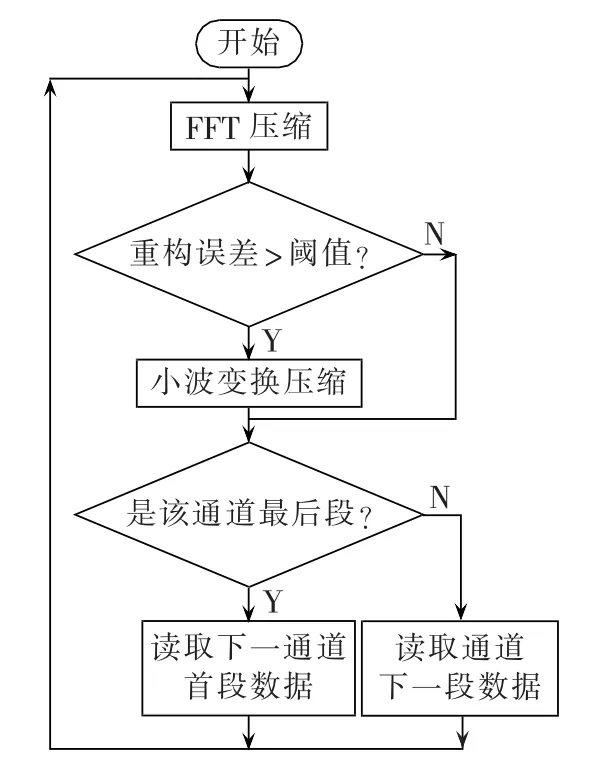
图2 数据压缩流程图Fig.2 Flowchart of data compression

对于正常通道数据采用FFT压缩。对于故障通道数据，由于A时段处在故障发生前，此时系统是正常运行的，采用 FFT压缩；而 B、C、D、E时段包含了故障暂态信息，具有显著局部特性，FFT已不适用，考虑采用具有时域局部化特性的小波变换压缩。

3 压缩方案实现中的关键技术

3.1 DFT频率校正及压缩方法

录波数据采样频率一般是工频的整数倍，当电网处于额定工频时，对于稳态周期信号，FFT算法具有良好的性能，压缩比高，误差小；但当电网基频偏离额定频率时，频谱泄漏效应会导致FFT压缩算法压缩比大幅降低，同时压缩误差明显增大。现采用DFT校正技术来解决这一问题，可在有较大频率偏移时保证稳态信号压缩的高精度、高压缩率。

3.1.1 DFT 校正方法[11]

以采样周期Ts对模拟量信号u（t）等间隔采样，得离散序列｛u（n）｝，再用长度为 N 的窗序列｛w（n）｝对｛u（n）｝加权截断，得到序列 uw（n）=u（n）w（n）（n=0，1，2，…，N-1）。 设信号 u（t）为一个单频率为 f1的不含谐波的信号，且离散窗序列w（n）的频谱W（f）具有线性相位，则在f=f1附近近似有：

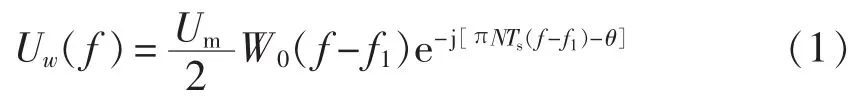
其中，W0（f）为一实函数。 Uw（f）的相位谱为：

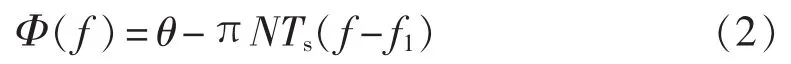
以 f0=1/（NTs）为采样频率对 Uw（f）进行抽样，可得序列｛uw（n）｝的 DFT Uw（k）及其相位 Φ（k），设f1=（k0+ α）f0（-0.5≤α≤0.5），即信号频率 f1接近 k0f0，若能求得 α，即可求得 u（t）的频率、幅值和相位为：

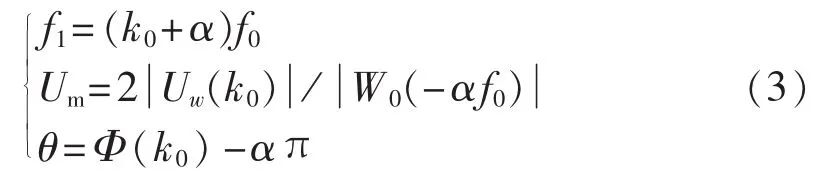
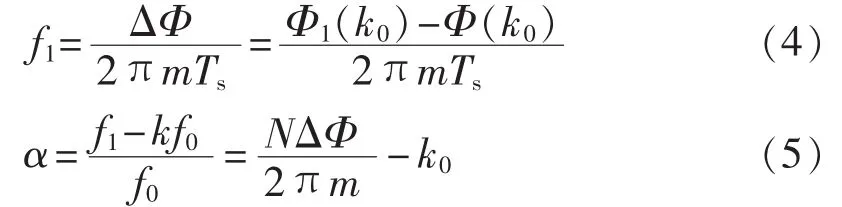
3.1.2 频率校正后压缩方法

对录波通道数据进行上述算法处理求得α后，采用式（3）计算得到基波及各次谐波的频率、幅值和相位，设置相关阈值滤除能量成分不高的谐波，并以正弦波形式重构近似周期信号，再进行FFT压缩。后续仿真结果表明，对频率偏移的信号进行频率校正后的FFT压缩，其压缩比大幅提升，误差减小。

3.2 小波分解结构及最佳分解层次

在MATLAB中，根据给定的小波变换函数，求解原始信号的多尺度分解，分解层数为Nd，函数返回分解向量C和长度向量L。图3是Nd=3的多尺度分解结构图[9]，信号x经过3层分解后在C序列中存储4个系数，分别是近似系数cA3（表征信号本身特征的低频系数）和细节系数 cD3、cD2、cD1（表征信号细微差别的高频系数），序列L中存储各个系数的长度。

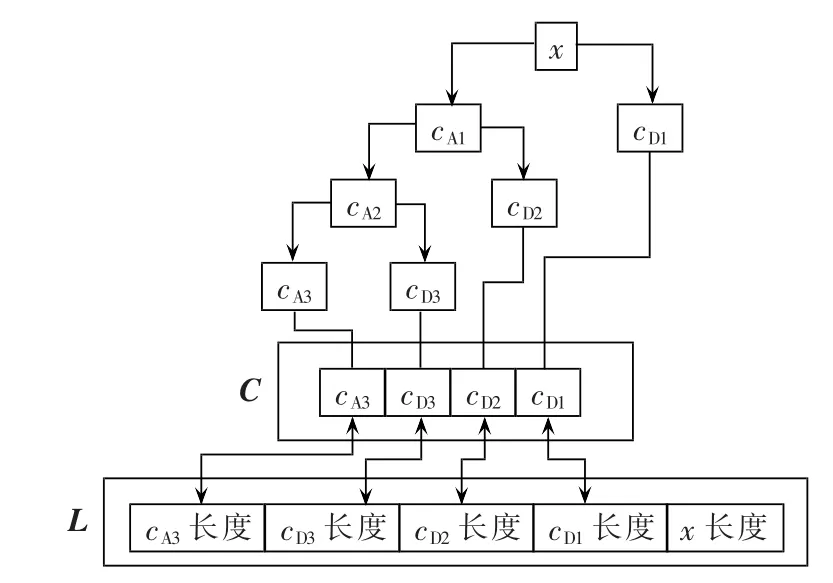
图3 小波变换分层结构图（3层）Fig.3 Hierarchical structure of wavelet transform（3 layers）

为了保证重构信号与原始信号的近似度，应使最底层近似系数包含工频成分，因此本文以式（6）确定最大分解层数[1]：

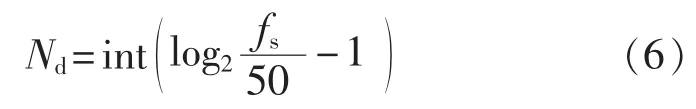
其中，int表示取整；fs为采样频率，电力系统工频为50 Hz。

3.3 小波作用阈值的确定

输电线路故障时，暂态信息主要隐藏在信号的畸变点上，通过设置阈值来舍弃幅度较小的无关小波系数。其基本原理是，设置某一尺度j下的阈值[5]为：

其中，M为原始信号的数据长度；dj（n）为小波分解后的细节系数；λ为比例系数，且0≤λ≤1，λ=0.1表示阈值设置为小波细节系数最大值的10%。

信号经过J级压缩处理后，重构信号的小波细节系数为：

1.3 统计学方法 将所收集的数据由双人录入EpiData 3.1软件，统计学处理通过SPSS 22.0软件完成。计数资料以百分比表示，采用χ2检验；计量资料以x±s表示，采用t检验。以P<0.05为差异有统计学意义。

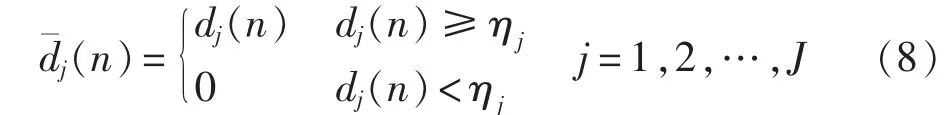
所以只需存储和传输信号较少的数据，即小波分解得到的低频系数和高频系数，这样就实现了对原始数据的压缩。当需要原始数据时，可以根据小波的重构公式计算存储的数据恢复信号。

4 仿真及压缩实例

4.1 FFT和小波压缩的选择判断

本文采用华中电网某220 kV变电站110 kV线路真实故障B时段录波数据作为仿真验证样本，采样频率为2 kHz。图4、图5分别是FFT压缩和小波压缩的效果图。其中FFT压缩阈值设置为fft（u）最大值的0.3%，小波压缩采用coif5小波基，分解层数为4，比例系数λ=0.001。

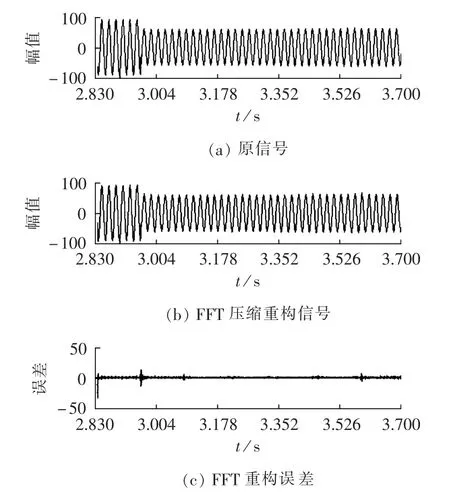
图4 实际故障信号F F T压缩重构图Fig.4 FFT compression and reconstruction of actual fault signal

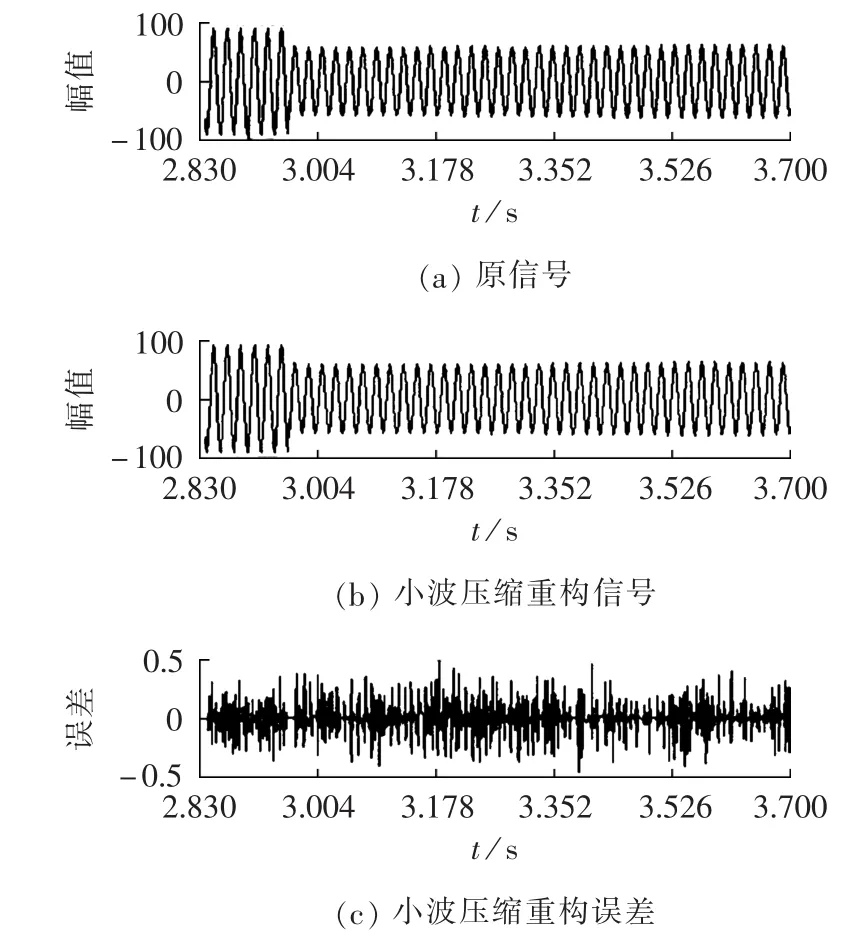
图5 实际故障数据小波压缩重构图Fig.5 Wavelet compression and reconstruction of actual fault signal

从图4和图5可以看出，FFT在压缩故障信号时，重构信号对故障信息反映不够精细，且有较明显的边界效应，误差很大。而小波压缩能精确重构故障信号，确保故障信息不丢失，且误差相对很小。以此为判据，在对信号进行FFT压缩后，如果误差很大，则改用小波压缩。

4.2 频率偏移对FFT压缩的影响

压缩包含基波及3、5次谐波成分的周期信号u，采样频率为2 kHz。阈值分别为fft（u）最大值的0.3%、0.5%、0.7%。图6为FFT压缩后不同阈值下剩余数据百分比与频率的关系曲线，剩余数据百分比=（1-零系数个数/系数总数）×100%。

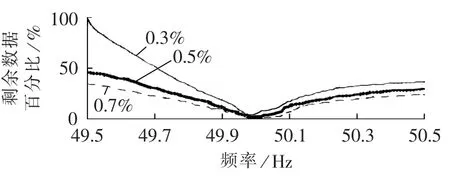
图6 不同阈值下压缩剩余数据百分比与频率关系曲线图Fig.6 Curves of relation between residual data percentage and frequency for different thresholds

图中3条曲线表明阈值越小，压缩后的剩余数据越多；另外，频率偏移越大，剩余数据百分比也越大，在工频50 Hz处，可以获得剩余数据百分比最小值1.5%。

图7是不同阈值下的最大误差百分比与频率的关系曲线，其中最大误差百分比为重构信号与原信号之间误差最大值和原信号最大值的百分比。从图中可以看出，在信号频率偏移工频50 Hz时，最大误差百分比明显增大，最大可达29%左右，只有在工频处，误差才会降到零。阈值设置得越小，保留的细节部分越多，误差也会更小，这也是图中0.3%曲线误差小于0.5%和0.7%曲线误差的原因。

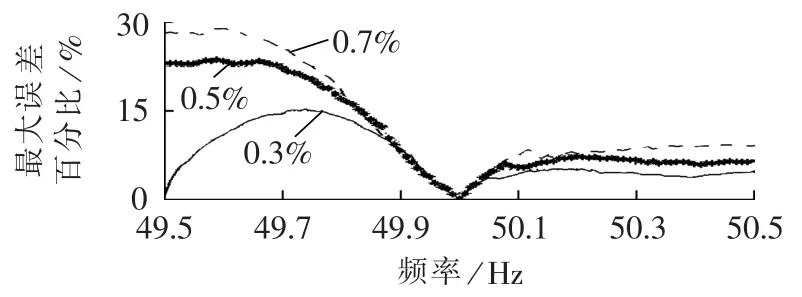
图7 不同阈值下最大误差百分比与频率关系曲线图Fig.7 Curves of relation between maximum error percentage and frequency for different thresholds

从图6、图 7可以看出：频率偏移50 Hz时，剩余数据百分比较大，误差也较大，重构数据不能精确地反映原信号特征，压缩性能不能达到最优，因此需要对信号进行频率校正再进行压缩；剩余数据百分比和最大误差百分比是一对成反比关系的性能指标，要获得较小的剩余数据百分比，阈值设置需要较大，而这时的误差也会相应地增加，因此，在实际中应根据指标要求设置阈值。

4.3 频率校正FFT压缩

在 MATLAB 中，以包含基波及 3、5、7、11次谐波（电力信号一般很少含偶次谐波）的余弦周期信号为原信号，采样频率2kHz，采用圆周对称的bartlett窗，其频谱数学表达式为：

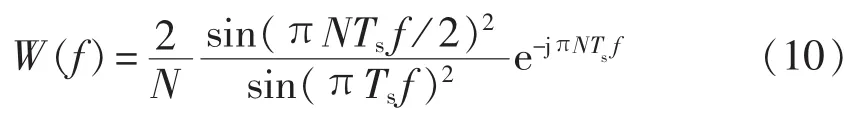
故障录波分析属于离线分析，为了提高压缩性能，减小误差，本文窗长度取400，谐波测量最高次数为10次。

图8是信号频率等于49.9 Hz，采用FFT测量压缩算法的重构信号及误差图。通过原信号和重构信号的比较能够发现，重构信号能精确恢复原始信号所携带的信息，误差非常小，零系数成分（即压缩后零系数个数/系数总数的百分比）达到97%。

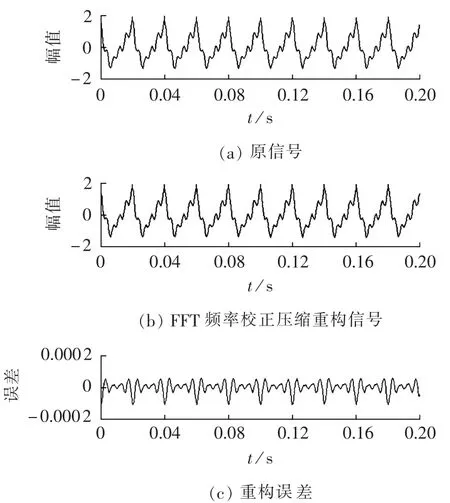
图8 理想信号FFT频率校正压缩重构图Fig.8 Compression and reconstruction of FFT with frequency calibration for ideal signal

图9中原信号数据采样频率为2 kHz，数据长度为400，谐波测量最高次数为20次，误差控制在±0.5%内，零系数成分为98.5%。

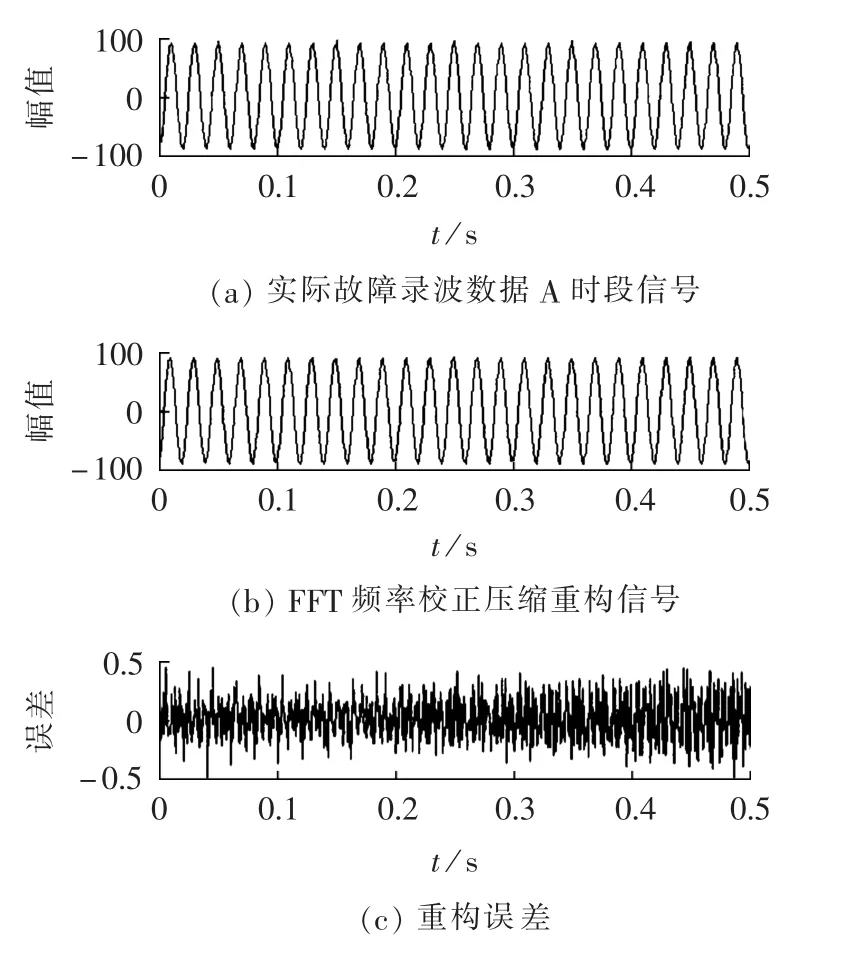
图9 单相接地故障A时段录波数据压缩重构图Fig.9 Compression and reconstruction of singlephase grounding fault records for segment A

4.4 录波数据整体的压缩性能

对电网实际故障录波数据分通道分时段压缩，零系数成分及压缩时间（取多次测试后最大值）结果分别如表1、表2所示。表1中通道1、2、3、4分别为该线路的A、B、C三相电流和3倍零序电流。

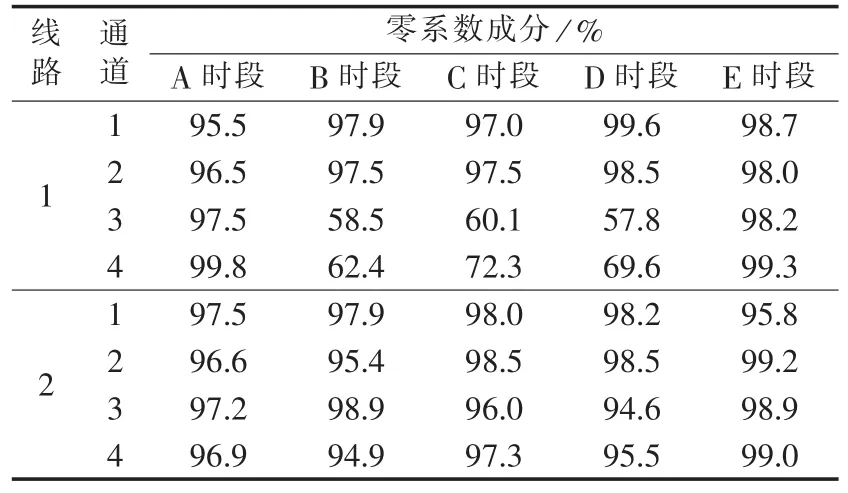
表1 实际录波数据整体压缩性能Tab.1 Overall data compression performance of actual records

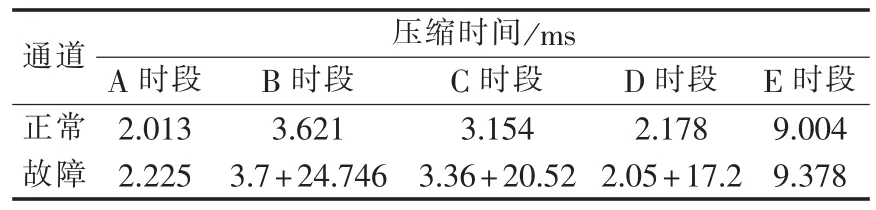
表2 实际录波数据压缩时间Tab.2 Data compression time of actual records

线路1发生了C相单相接地故障，即通道3、4的B、C、D时段是故障时段，在FFT压缩判断后改用小波变换进行压缩，由于数据携带故障信息丰富，且小波分解层数为4层，故零系数成分较少，压缩时间较长。

线路1的通道1、2全部时段和分别处于故障前和切除故障后的通道3、4的A、E时段以及线路2所有通道的各时段都是正常运行数据，采用FFT频率校正压缩，零系数成分比较高，一个正常通道所有时段的压缩时间总计19.97 ms。

综上所述，如果本地存储压缩后的数据，采用本文算法可整体上节约80%以上的存储空间，极大地降低了存储成本。在实时传输方面，以一个通道数据为例，压缩前数据大小约为10244×2字节，FFT压缩后由于只需记录非零值采样点采样编号及其FFT变换系数值，其大小为618字节。如果通过以太网发送（以太网数据帧最大长度1500字节），只需一次即可发送完毕，减少了网络流量，降低了CPU资源占用量。

5 结论

本文立足于整体录波数据，提出了一种分通道分时段数据压缩方案，即采用FFT算法分段压缩数据，若数据重构后误差较大，则改用小波变换压缩。当频率偏移较大时，常规FFT算法的压缩误差较大，剩余数据百分比较高，这时可采用基于DFT校正算法的改进FFT压缩方法。通过理想数据和实际故障录波数据的仿真测算，验证了算法较高的压缩性能，以及重构信号良好的信息保留特性。该方案在电力系统故障录波数据压缩中的应用是可行的。