降雨条件下软岩边坡渗流-软化分析方法及其灾变机制

谢瑾荣 ，周翠英，程 晔

（1. 中交第四航务工程勘察设计院有限公司，广州 510230；2. 中山大学 工学院，广州 510275）

1 引 言

降雨条件下软岩边坡的渗流-软化效应是滑坡领域研究的热点与难点问题。一般而言，降雨引起的边坡失稳是由于雨水入渗导致边坡内部孔隙水压力场升高所致。对于软岩边坡而言，软岩的遇水软化效应也是边坡灾变的重要原因。因而研究降雨条件下软岩边坡的渗流-软化灾变效应对软岩边坡工程的安全评价具有重要意义。

由于软岩的水-岩耦合作用机制具有高度的复杂性，目前有关软岩边坡降雨-渗流-软化的系统分析尚处于探索阶段，尤其是对于软化效应的考虑还存在一定不足。汪益敏[1]和刘祚秋[2]等在进行软化效应分析时，根据经验判断降雨的入渗深度，将软岩软化残余强度直接代入到入渗深度内的岩体中进行软化效应分析，该方法计算简便，但忽略了软岩软化区域和软化程度的变化，不利于全面揭示软岩边坡在降雨环境下的失稳演化规律，其计算结果较难反映软岩边坡实际的破坏形式和失稳模态。付宏渊等[3]根据降雨发生后软岩边坡中暂态饱和区范围来判定边坡软化区域，使分析具有一定的定量性，但对于如何根据暂态饱和区确定不同降雨历时下软岩边坡的软化区域及其软化程度的研究尚不够充分。另外，在进行边坡降雨渗流分析时，对于降雨入渗的考虑常带有一定估计性[4]，常用的方法有折减雨强法、特征线法、完全耦合法和间接耦合法等[5]，其中，折减雨强法和特征线法分析时未考虑坡面径流的影响，也未考虑边坡的几何形态及边界条件的变化，与实际情况差异较大；完全耦合法将降雨-径流-入渗视为统一的系统，建立总体耦合方程，但是迭代求解计算量大，采用该方法进行软岩边坡渗流-软化效应分析，工作效率较低；间接耦合法是基于有限元模型建立的耦合问题直接求解法，计算结果较为接近实际情况，计算效率较高，适用于数值分析问题。鉴于此，本文采用间接耦合法进行降雨入渗分析，并基于暂态饱和区建立了软岩边坡降雨-渗流-软化-灾变的数值分析方法，并重点研究了降雨条件下软岩边坡的渗流-软化灾变机制。

2 软岩边坡渗流效应分析方法

2.1 软岩边坡降雨入渗模型

降雨条件下，边坡表面的雨水入渗可分为两个阶段，一个是地表径流形成前的完全入渗阶段，另一个是地表径流形成后的有压入渗阶段。雨水入渗软岩的强度又称为入渗率。在降雨初期，降雨的强度小于软岩的渗水性能时，入渗率等于降雨强度，软岩中的含水率会随着地表水的下渗而逐渐提高以至达到一个极限值。如果降雨继续发生，且降雨强度不变或增加，那么来自外界的供水强度就超过了软岩的渗水能力，边坡地表就会形成径流或积水，此时的入渗率等于软岩自身的渗水能力。

本文采用间接耦合法进行软岩边坡降雨入渗分析，分析模型示意图见图1。

图1 降雨与入渗耦合分析示意图[5]Fig.1 Schematic of coupling analysis of rainfall and infiltration

地表水分析时采用吴长文等[6]推导的适合于陡坡、裸地的坡面流方程为

由于运动波理论可以较好地描述坡面径流的运动过程，且计算简单，因而本文采用一维运动波模型来描述，而动量方程可以采用曼宁公式代替，替换后方程如下：

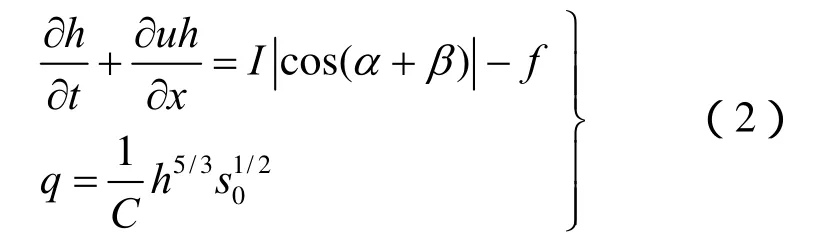
式中：q为单宽流量；C为坡面粗糙度系数。式（2）的初始条件为

边界条件为

将以上方法应用于软岩边坡降雨入渗分析中，实现步骤如下：

（1）首先将降雨强度作为初始流量边界条件施加在斜坡表面，通过地下水分析模块求解初始孔隙水压力场，地下水分析模块采用软岩边坡非饱和-饱和渗流分析法，详见本章2.2节。

（2）通过表层软岩是否达到饱和，判断是否产生地表径流。如果在某一时刻表层软岩未达到饱和，则降雨全部下渗到边坡内部，继续将降雨强度作为流量边界进行下一个时间步的渗流计算；如果边坡下渗量小于或等于降雨强度，则认为此时边坡表层软岩达到饱和。

（3）此时将地表各节点剩余流量代入地表水分析模块，计算相应的积水深度。

（4）将地表积水深度作为水头边界条件施加在边坡表层进行下一步地下水分析计算，直至降雨结束。

2.2 软岩边坡非饱和渗流-应力计算原理

由于软岩中大量孔隙、裂隙的存在，使软岩边坡地下水位以上部分处于非饱和状态。非饱和软岩的渗水能力与软岩种类、孔隙状态、流体特性及其其饱和程度密切相关。在饱和区，软岩的渗透系数可以假定为常数，但在非饱和区，其渗透系数往往要小于饱和区的软岩，这是因为液体状态的水沿连续路径流动，当含水率减少时，流径的大小和数量将减小，因而流动的水量也就减少。

基于本文对软岩边坡降雨灾变效应的研究属于宏观尺度问题，在进行非饱和渗流-应力分析时将软岩看作多孔介质，将多孔介质内的气体视为理想气体，内部流体遵循达西渗流定律[7]。因此，本文在对软岩边坡进行非饱和-饱和渗流分析时，采用Richards的控制方程，将非饱和区软岩的渗透系数表示为与饱和度、基质吸力或体积含水率相关的函数，描述如下：

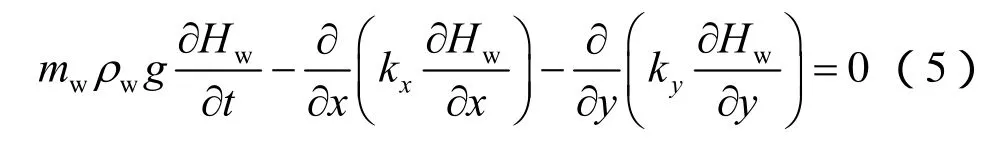
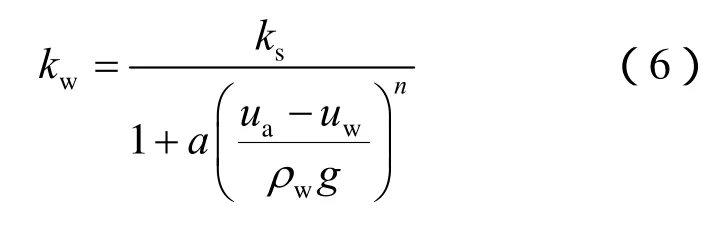
式中：ua为孔隙气压力； ua-uw为基质吸力；a、n均为加德纳系数；ks为饱和渗透系数；kw为非饱和渗透系数。

基质吸力与含水率的关系采用 Van-Genuchten模型表示：

式中：l、m、t均为非线性回归系数；θs和θr为饱和含水率和剩余含水率。

在进行渗流-应力计算时采用四自由度全耦合分析法[7－8]，根据Galerkin加权余量法及格林公式，求解此类有限元方程时采用全隐式向后差分的方法，求解渗流场的有限元法方程为

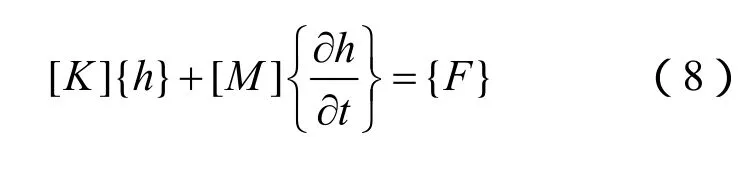
其中：

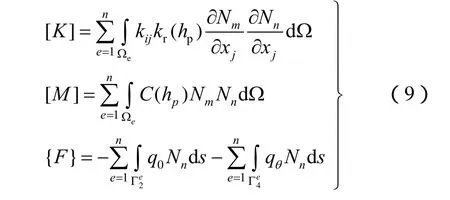
3 暂态饱和区的渗流-软化分析方法

降雨入渗条件下渗流场变化将导致软岩边坡内部孔隙水压力暂时升高，含水率增加，基质吸力降低，软岩由非饱和状态向饱和状态转变。当孔隙水压力升高为正值时，边坡内相应的区域被称为暂态饱和区[9]。工程实践[10]显示，软岩边坡暂态饱和区内的软岩体将发生软化，而文献[11]的研究结果也证明了软岩软化是软岩中孔隙水压力升高，含水率增加，孔隙饱水膨胀，颗粒连接开始松散，局部连接方式发生改变所致。同时，根据软岩饱水试验原理[12]可知，该试验最大程度模拟了软岩在实际中的饱水软化过程，通过饱水状态下的三轴破坏试验，可测定不同饱水时间下的软岩饱水软化抗剪强度指标。基于以上分析，本文将降雨过程中边坡内部出现的暂态饱和区与边坡的实际软化区相联系，将试验测得的软岩软化特征赋予暂态饱和区中对应的软岩体，再通过判定暂态饱和区的出现区域及持续时间，来模拟软岩边坡的实际软化区域和软化程度，从而实现软岩边坡软化效应的考虑。

计算模型中单元赋值准则如下：①在计算不同降雨历时下各暂态饱和区对应的软岩软化时间时，用计算的降雨历时减去各暂态饱和区出现时对应的降雨历时，就等于各暂态饱和区内软岩的软化时间（暂态饱和区未出现时，认为其内软岩还未发生软化），此时各暂态饱和区内软岩的抗剪强度参数就对应软岩遇水软化试验中此软化时间下的抗剪强度参数。②停雨以后，仍处于暂态饱和区范围内的软岩软化时间，应加上停雨时间，而原属于暂态饱和区以内，停雨以后处于暂态饱和区以外的软岩体，认为其抗剪强度等于其前一计算时刻的抗剪强度。

为使分析更接近于实际情况，需将渗流与软化相结合，对软岩边坡进行降雨条件下的渗流-软化灾变效应分析。综合前文所述方法，建立基于暂态饱和区的软岩边坡降雨-渗流-软化-灾变的数值分析方法，具体实现步骤如下：

（1）计算地层的初始地应力，并将模型的初始位移清零；

（2）通过生死单元模拟开挖，获取边坡应力重分布结果；

（3）进行降雨入渗分析，获取边坡的雨水入渗量及其表面的积水深度，作为渗流计算的边界条件；

（4）进行软岩边坡非饱和-饱和渗流分析，获取不同降雨历时下的渗流场计算结果，并根据孔隙水压力值确定某一降雨历时下的暂态饱和区分布情况；

（5）通过软岩遇水软化试验，确定边坡软岩抗剪强度的遇水软化特征；

（6）将步骤（4）中处于暂态饱和区内的软岩体抗剪强度与软岩遇水软化试验中所测得的指标值通过饱水时间相互对应；

（7）根据步骤（6）中软岩抗剪强度参数动态修改某一降雨历时下边坡暂态饱和区内的单元参数；

（8）将步骤（4）中与步骤（7）对应的渗流场计算结果输入到有限元模型中；

（9）进行软岩边坡渗流-软化效应分析，采用非饱和有限元强度折减法计算该降雨历时下的边坡稳定性；

（10）返回步骤（4），进行不同降雨历时下的软岩边坡渗流-软化效应分析，并计算其稳定性变化情况。

在进行稳定性分析时，采用迭代求解不收敛作为边坡失稳的判据，收敛条件为内力范数小于0.03，将最大塑性剪切带作为边坡潜在的失稳滑动面[2]。

4 软岩边坡渗流-软化灾变机制

4.1 工程概况及模型建立

为检验本文分析方法的正确性，将文献[1]中的软岩高边坡工程作为实例分析对象。该边坡为东深供水改造工程中K13+785～885段渠道边坡。其中左岸边坡自下至上共分为5级，每级坡比均为1:1.5，其中第1、2级边坡坡高为5 m，第3～5级边坡坡高为10 m。边坡防护措施为：第1、2级边坡采用C20混凝土现浇防护，并设φ50 mm排水孔；第3、4级边坡采用挂钢筋网喷射混凝土防护，未设排水孔；第5级边坡采用植物防护坡面，见图2。

边坡表面坡积层土壤在施工时已清除，剩余地层自上往下描述如下：①全、强风化泥质粉砂岩，风化强烈，节理裂隙发育，岩质软弱，吸水后强度指标显著降低，软化严重，分布厚度为15～30 m；②弱风化粉细砂岩，岩质稍硬，坡脚12 m深度以下范围分布。

采用非线性有限元软件MIDAS-GTS根据边坡实际情况建立模型。模型尺寸及边界条件示意图如图2所示，模型两侧及底部为位移约束边界，根据边坡排水条件，左岸第1、2级边坡及右岸第1、2级边坡为透水边界且为溢出边界，左岸第 3、4级边坡为不透水边界，左岸坡顶及其第5级边坡和右岸坡顶均为降雨入渗边界。经过网格划分，模型共3 675个单元、3 848个节点，见图3。计算所采用参数见表1，软岩非饱和特性见图4[12]。

图2 边坡示意图Fig.2 Schematic of slope

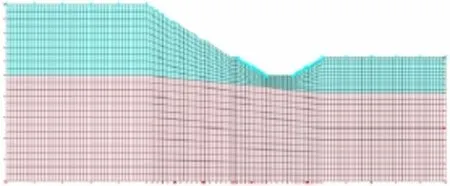
图3 有限元模型Fig.3 Finite element model

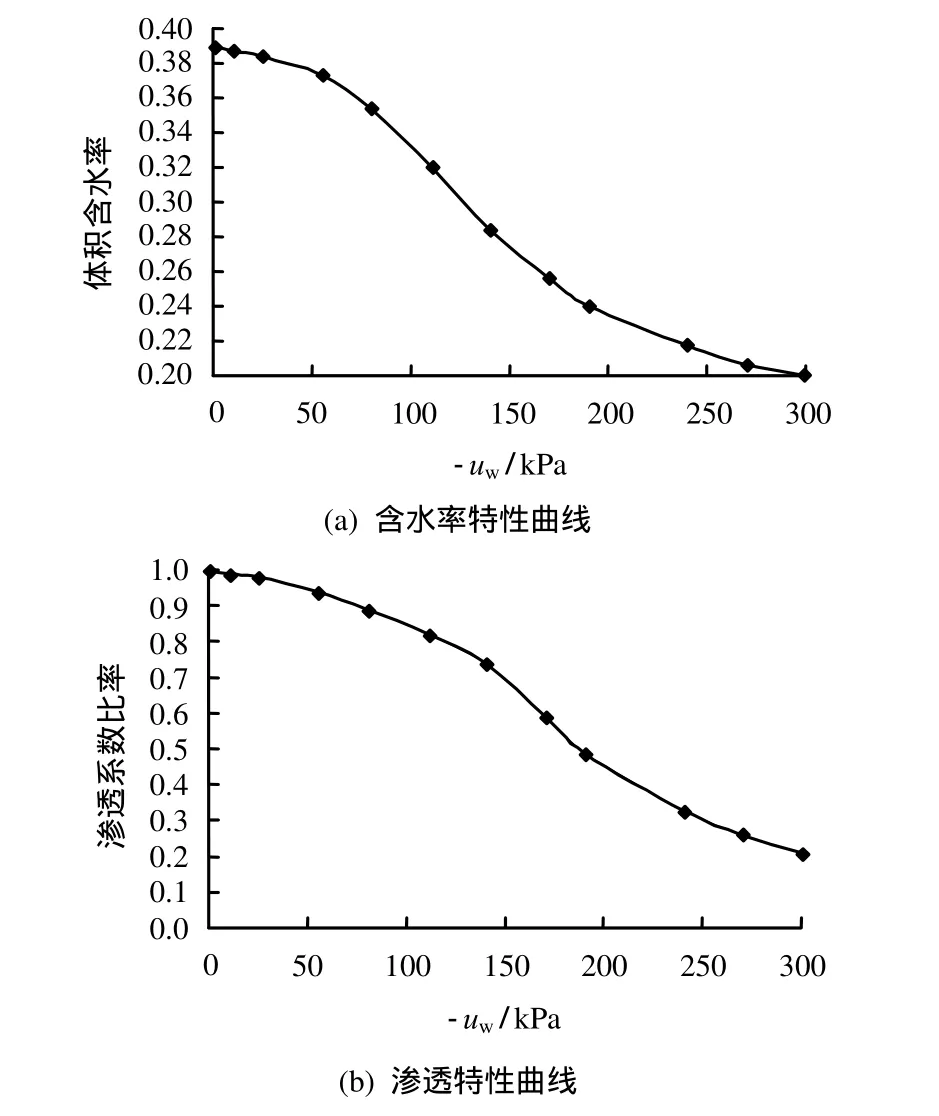
图4 软岩非饱和特性曲线Fig.4 Unsaturation characteristic of soft rock

该地区雨量充沛，年平均降雨量在 2 000 mm以上，其中 4～6月降雨量约占全年总降雨量的70%，其平均日降雨量分别为10、15、12 mm/d，其中6月最大日降雨量达到100 mm以上[1]。

表1 岩土材料参数表Table 1 Geotechnical material parameters

4.2 渗流-软化灾变机制分析

经降雨入渗分析，得到边坡入渗率及积水深度情况如图 5所示，将其作为边界条件进行非饱和-饱和渗流分析，得到边坡在降雨条件下孔隙水压力场的变化情况如图6所示，其中分析时间点分别为降雨15 d、30 d、45 d、60 d、75 d、90 d，受篇幅所限，仅列出部分结果。

图5 坡面入渗率和积水深度Fig.5 Slope infiltration rate and water depth

从图6中可以看出，随着降雨的进行，两岸边坡内部孔隙水压力值逐渐增大。至降雨30 d，即4月底时，两岸边坡坡顶孔隙水压力值大于或等于0，边坡内部出现暂态饱和区，其深度约为坡表以下2～4 m。降雨60 d时，左岸边坡坡顶后方暂态饱和区深度已开展至坡表以下9 m，但第5级边坡坡面以下暂态饱和区深度仅为2 m左右。至降雨75 d时，暂态饱和区向下开展至第4级边坡中部，孔隙水压力场自坡表向内大致呈“正—负—正”的分布态势。直至降雨90 d，分析计算结束时，第1～3级边坡坡表以下均未出现暂态饱和区，此处岩体未发生饱水软化，这是因为第1～4级边坡均为混凝土护面，其中第1、2级边坡为排水条件，第3、4级边坡为不透水条件，不直接受到降雨入渗的影响，加之渗流补给水从底部边坡排水溢出，因而此处岩体未达到饱和；第5级边坡未采用混凝土护面，为渗水边界，在降雨过程中容易发生饱和；第4级边坡由于距离第5级边坡较近，离底部排水边界较远，因而受第5级边坡的雨水入渗影响较大，在第5级边坡岩体饱和之后也出现了暂态饱和区。

图6 边坡孔隙水压力场随降雨历时变化图Fig.6 Changes of slope pore water pressure field with rainfall duration

对渗流分析结果进行后处理，以网格节点的孔隙水压力值是否大于0为判据，识别出不同降雨历时下的边坡暂态饱和区（见图7），其边界曲线内部即对应该边坡发生软化的区域，这与文献[1]中将地表以下4 m范围内认定为饱水软化区有所不同，本文结果考虑了饱水软化区随时间和空间分布与变化，更符合工程实际。再根据前文所提出的渗流-软化效应分析方法对暂态饱和区内的单元进行动态赋值，并导入对应的孔隙水压力场，然后采用非饱和强度折减法进行降雨条件下边坡稳定性分析，其中边坡模型的单元赋值情况见图8。

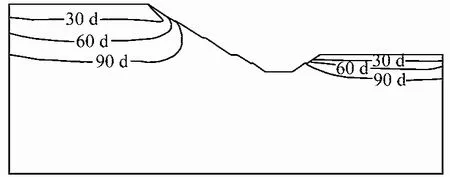
图7 暂态饱和区示意图Fig.7 Schematic of transient saturated zone

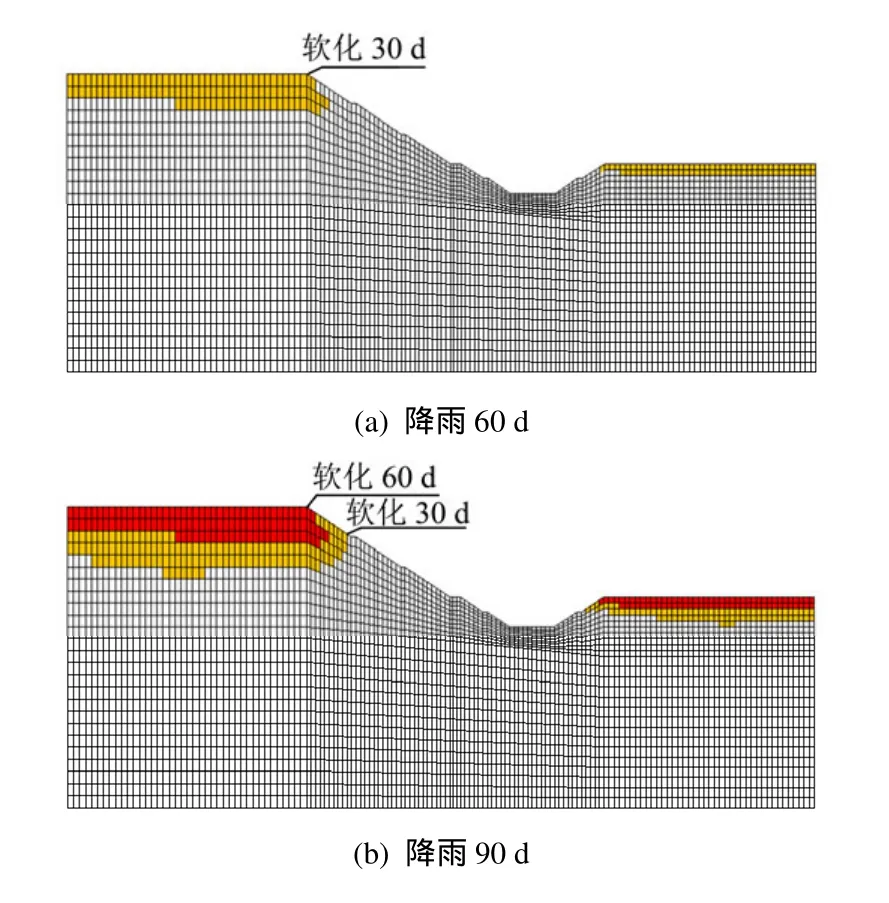
图8 单元赋值情况Fig.8 Case of unit assignment

经分析，得到不同降雨历时下边坡深部水平位移、潜在滑动面、安全系数如图9～11所示。

从图9中可看出，降雨15 d前的边坡深部水平位移量较小，变化较为稳定，降雨30 d时，深度4～5 m处的水平位移量已明显增大，且变化速率不收敛，降雨90 d时边坡已处于失稳破坏阶段。图10为边坡潜在滑动面变化情况。从图中可知，随着降雨的进行，边坡的潜在滑动面深度逐渐由深变浅，剪出面逐渐向上发展。降雨前边坡潜在滑动面最深处距坡表垂直距离约为12 m，降雨结束时约为8 m；降雨前，潜在滑动面从坡顶贯通至坡脚，随后由底部逐渐抬高；降雨 60 d时，潜在滑动面剪出口上升至第3级边坡坡脚处。该边坡的实际情况[1]是，工程竣工后，经历持续降雨季节，期间左岸第 2、3级边坡发生明显变形破坏，其中第3级边坡坡面鼓出严重，其下方岩体向临空方向产生剪切变形。工程实际破坏形态与本文模拟结果相符，说明本文分析方法与结果具有一定合理性和正确性。

从图11可知，边坡安全系数-时程曲线大致呈反向复曲线形态，渗流效应对该边坡稳定性的影响主要发生在降雨前期，其后趋于稳定；降雨历时45 d时，其安全系数-时程曲线出现明显拐点，其后边坡稳定性快速降低；渗流效应导致该边坡安全系数降低 7%，软化效应导致该边坡安全系数降低27%，软化效应对边坡稳定性影响大于渗流效应；在渗流-软化综合效应下，边坡安全系数最低为1.12，降幅达到 39%，边坡安全性已大幅降低，且低于规范要求。

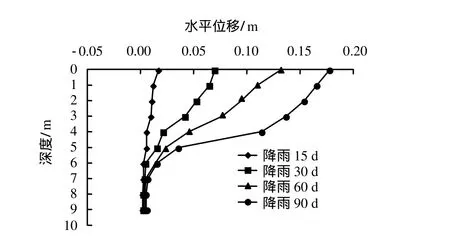
图9 第3级边坡平台处深部水平位移情况Fig.9 Deep horizontal displacement at the third slope platform

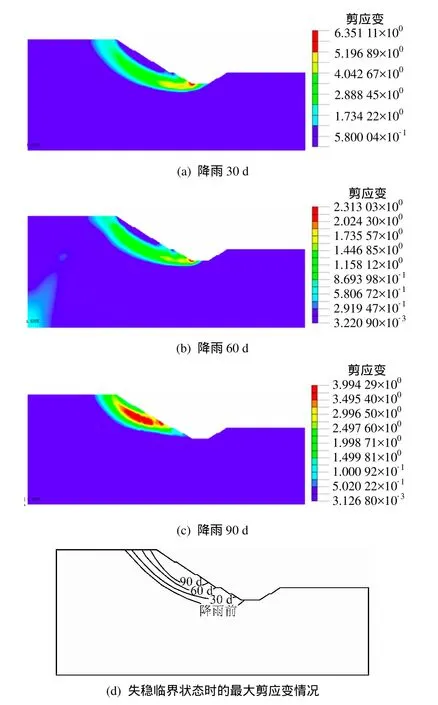
图10 边坡潜在滑动面变化图Fig.10 Changes of potential sliding surface of slope

图11 边坡安全系数-时程曲线Fig.11 Time curves of slope safety factor

5 结 论

（1）降雨发生后边坡浅部软岩逐渐由非饱和状态逐渐向饱和状态转变，边坡顶部率先出现暂态饱和区，并逐渐延伸至坡脚，孔隙水压力场自坡表向内大致呈“正—负—正”的分布态势。

（2）降雨条件下软岩边坡灾变的主导效应与软岩特性、软岩赋存面积以及降雨条件等因素有关。一般情况下，降雨前期渗流效应对软岩边坡稳定性的作用占主导地位，降雨后期和停雨后软岩软化效应的影响更为明显。

（3）由实例分析结果可知，降雨条件下边坡的潜在滑动面随降雨时间逐渐变浅；安全系数-时程曲线呈反向复曲线形态，软岩开始软化时，曲线上出现拐点，边坡稳定性开始显著下降，并由潜在滑动状态向失稳破坏演变，这表明软化效应加速了软岩边坡在降雨条件下的失稳演化进程。

[1]汪益敏, 陈页开, 韩大建, 等. 降雨入渗对边坡稳定影响的实例分析[J]. 岩石力学与工程学报, 2004, 23(6):920－924.WANG Yi-min, CHEN Ye-kai, HAN Da-jian, et al. Case study on influence of rainfall permeation on slope stability[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(6): 920－924.

[2]刘祚秋, 周翠英, 董立国, 等. 边坡稳定及加固分析的有限元强度折减法[J]. 岩土力学, 2005, 26(4): 558－562.LIU Zuo-qiu, ZHOU Cui-ying, DONG Li-guo, et al.Slope stability and strengthening analysis by strength reduction FEM[J]. Rock and Soil Mechanics, 2005,26(4): 558－562.

[3]付宏渊, 曾铃, 王桂尧. 降雨入渗条件下软岩边坡稳定性分析[J]. 岩土力学, 2012, 33(8): 2359－2363.FU Hong-yuan, ZENG Ling, WANG Gui-yao, et al.Stability analysis of soft rock slope under rainfall infiltration[J]. Rock and Soil Mechanics, 2012, 33(8):2359－2363.

[4]谢瑾荣, 周翠英, 程晔, 等. 基于非饱和土有限元强度折减法的降雨入渗条件下高边坡施工稳定性分析[J].水运工程, 2012, (4): 179－184.XIE Jin-rong, ZHOU Cui-ying, CHENG Ye, et al.Construction stability analysis of high slope under rainfall infiltration based on FEM strength reduction of unsaturated soil[J]. Port & Waterway Engineering,2012, (4): 179－184.

[5]刘俊新, 刘育田. 考虑非饱和地表径流-渗流耦合条件下斜坡降雨入渗在 FLAC中模拟[C]//第一届全国工程安全与防护学术会议论文集, 南京: [出版者不详],2008.

[6]吴长文, 王礼先. 林地坡面的水动力学特性及其阻延地表径流的研究[J]. 水土保持学报, 1995, 9(2): 32－38.WU Chang-wen, WANG Li-xian. Study on the dynamic characteristics of overland flow and resistance to overland flow of forested slopeland[J]. Journal of Soil Erosion and Water Conservation, 1995, 9(2): 32－38.

[7]陈卫忠, 邵建富, DUVEAU G, 等. 黏土岩饱和-非饱和渗流应力耦合模型及数值模拟研究[J]. 岩石力学与工程学报, 2005, 24(17): 3011－3016.CHEN Wei-zhong, SHAO Jian-fu, DUVEAU G, et al.Constitutive model of saturated-unsaturated clay and its numerical simulation[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(17): 3011－3016.

[8]顾成壮, 胡卸文, 张茂淳, 等. 强降雨下饱和平滑型滑坡坡体水流运动及其边坡稳定效应分析——以四川汉源二蛮山滑坡为例[J]. 岩土力学, 2013, 34(4): 1075－1081.GU Cheng-zhuang, HU Xie-wen, ZHANG Mao-chun,et al. Analysis of flow motion and its effect on the slope stability of plane sliding landslide saturated under heavy-rain—A case study of Ermanshan landslide in Hanyuan county of Sichuan province[J]. Rock and Soil Mechanics, 2013, 34(4): 1075－1081.

[9]付宏渊, 曾铃, 蒋中明. 降雨条件下公路边坡暂态饱和区发展规律[J]. 中国公路学报, 2012, 25(3): 59－64.FU Hong-yuan, ZENG Ling, JIANG Zhong-ming, et al.Developing law of transient saturated areas of highway slope under rainfall conditions[J]. China Journal of Highway and Transport, 2012, 25(3): 59－64.

[10]周家文, 徐卫亚, 邓俊晔. 降雨入渗条件下边坡的稳定性分析[J]. 水利学报, 2008, 39(9): 1066－1073.ZHOU Jia-wen, XU Wei-ya, DENG Jun-ye, et al.Stability analysis of slope under the condition of rainfall infiltration[J]. Journal of Hydraulic Engineering, 2008,39(9): 1066－1073.

[11]周翠英, 朱凤贤, 张磊. 软岩饱水试验与软化临界现象研究[J]. 岩土力学, 2010, 31(6): 1709－1715.ZHOU Cui-ying, ZHU Feng-xian, ZHANG Lei. Research on saturation test and softening critical phenomena of soft rocks[J]. Rock and Soil Mechanics, 2010, 31(6): 1709－1715.

[12]周翠英, 邓毅梅, 谭祥韶. 饱水软岩力学性质软化的试验研究与应用[J]. 岩石力学与工程学报, 2005, 24(1):33－38.ZHOU Cui-ying, DENG Yi-mei, TAN Xiang-shao, et al.Experimental research on the softening of mechanical properties of saturated soft rocks and application[J].Chinese Journal of Rock Mechanics and Engineering,2005, 24(1): 33－38.