软黏土加载速率效应特性试验研究：进展与趋势

朱启银，尹振宇，朱俊高，王建华，夏小和

（1. 上海交通大学 土木工程系，上海 200240；2. 河海大学 岩土工程研究所，南京 210098）

1 引 言

由于软黏土具有高黏粒含量、高含水率、大孔隙比等特点，使其力学性质不仅呈现出蠕变与应力松弛特性，而且也具有明显的加载速率效应，在宏观上表现为强度的加载速率相关性。早在 20世纪30年代，Buisman[1]通过室内试验研究指出，土体应力-应变-强度关系具有不可忽略的速率相关性。一般实际工程的应变速率（10-2～10-3%/h）和实验室常规试验的应变速率（0.5～5.0%/h）有很大差别[2－3]。因此，以实验室标准加载速度条件下取得的抗剪强度和先期固结压力作为工程设计依据而不考虑土的加载速率效应特征，将导致岩土工程结构物在施工阶段时失稳或工后长期沉降过大。基于此，黏土的应变率效应特性研究一直是土体基本性状探索的热点课题之一。

针对软黏土的加载速率效应特性，各国学者们对其进行了大量的试验研究：一维条件下的等应变速率（CRS）试验[4－12]、三轴条件下的不排水应变速率试验[7－9,13－23]以及复杂应力条件下的应变速率试验[24－26]等。然而，这些试验一般主要针对某种特定黏土，研究其在特定条件下（应力历史、固结状态和试验类型等）的应变速率效应，而较少从统一性上研究软黏土加载速率效应特性，在以下方面存在着不足：

（1）现有研究一般是将软黏土的一维先期固结压力和三轴不排水抗剪强度的速率效应分开来探讨，而对软黏土一维加载速率效应和三轴加载速率效应是否相关、有何相关性等鲜有提及。

（2）对应变速率效应在三轴压缩与伸长条件下的统一性和不同 OCR (超固结比)下的统一性都缺乏深入的探讨。

（3）应力剪缩/剪胀关系是土体的一个重要力学特性，为土体本构关系的基础之一[27－29]。然而，到目前为止，却很少有学者针对黏土加载速率对不同OCR条件下三轴压缩与伸长过程中应力剪缩/剪胀特性的影响进行深入的研究。

基于以上问题，笔者认为，有必要对现有试验成果做一综述和深入分析，为深入认识土体特性以及本构模型开发提供试验与理论基础（见图1）。本文首先对软黏土从一维到三轴、到复杂应力路径条件下的加载速率效应试验研究进行了系统的总结，并对不同速率方程进行探讨；接着，在一维和三维的统一性、压缩与伸长的统一性和不同 OCR的统一性上进一步深入讨论软黏土的加载速率效应；最后，基于香港海相黏土的试验结果，探讨加载速率对应力剪缩、剪胀关系在三轴压缩和伸长条件下以及在不同OCR条件下的影响。

2 试验研究进展

所谓的加载速率效应就是土体的应力及强度随着加载速率的增大而增大。图2为典型的土体等应变速率（CRS）试验曲线的示意图。在相同的应变条件下，当加载速率 c3＞ c2＞ c1（图 2(a)）时，与加载速率对应的应力σ3＞σ2＞σ1（图2(b)）。在本节中，笔者对黏土在不同应力条件下的加载速率效应特性进行了系统的总结，这包括：一维压缩、三轴压缩与伸长以及非常规的复杂应力。

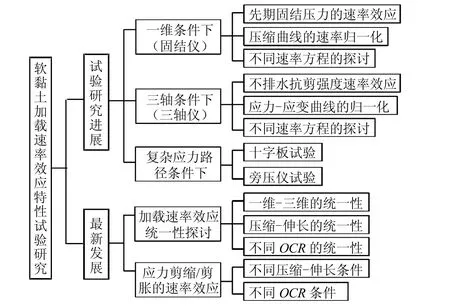
图1 研究内容框架Fig.1 Schematic illustration of research

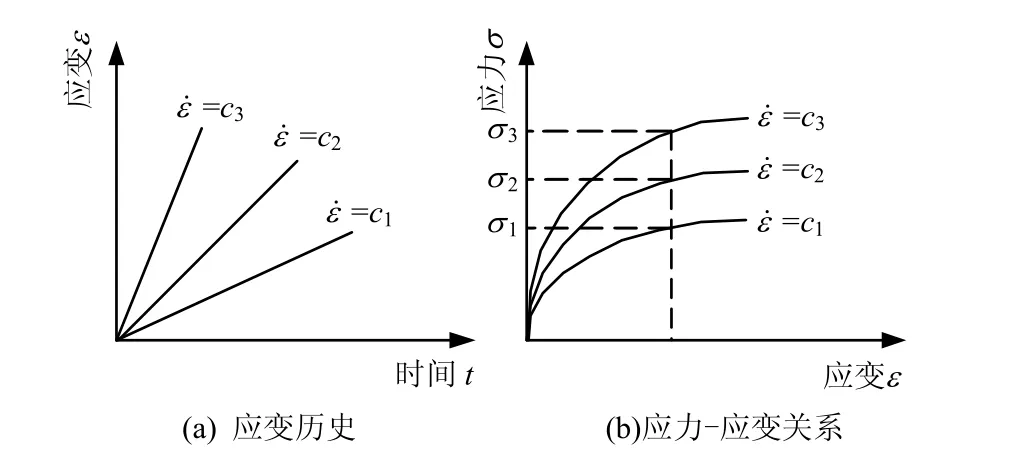
图2 等应变速率试验Fig.2 CRS tests

2.1 一维CRS试验

传统的一维 CRS试验就是在一维固结仪中对试样通过竖向恒定位移速度控制施加荷载，在试验过程中直接测量竖向应力和变形，进而得到两者之间的关系，以研究不同应变速率下土体固结特性。由于一维CRS试验是最简单的，也是最基本的研究土体应变速率效应特性的试验，是研究土体流变本构特性的基础之一。笔者基于前人所做的一维CRS试验结果，主要针对以下几个问题进行讨论：①先期固结压力的速率效应；②压缩曲线的速率归一化；③不同先期固结压力-速率方程的探讨。

2.1.1 先期固结压力的速率效应

众多一维 CRS 试验都表明[4－7,10－12,25]：加载速率越大，相应的先期固结压力σp′也越大（见图3(a)）。其中，Leroueil等[4]通过分析多地区黏土的一维CRS试验结果，系统地总结了黏土的一维应变率效应，并指出可以用等速率线[30]体系描述一维情况下先期固结压力与加载速率一一对应关系，即可以用下式来表达：

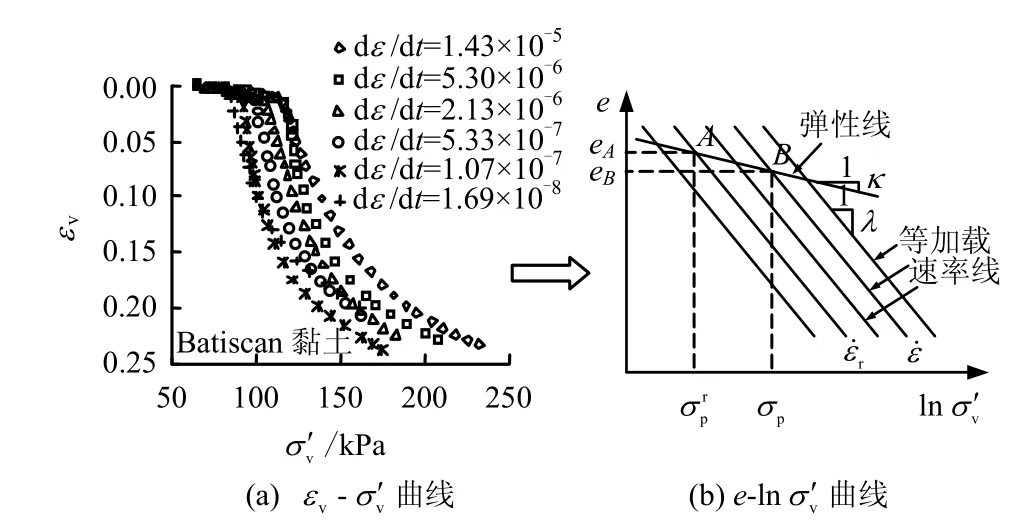
图3 一维CRS试验应力-应变-应变速率关系图Fig.3 Stress-strain-strain rate behavior of 1D CRS tests

为能够定量化地描述先期固结压力与加载速率的相关性，笔者总结了17种黏土CRS试验结果，并把先期固结压力与加载速率的关系绘于图 4。可以看出，图中所有土样的应变速率在0.002～27%/h之间，在此应变速率范围内σp′与加载速率成正比关系。

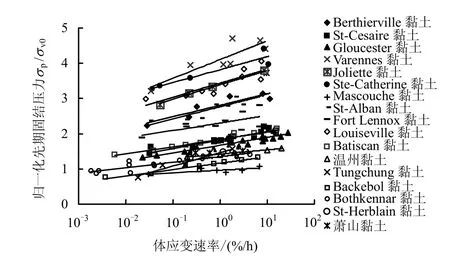
图4 先期固结压力与应变速率的关系Fig.4 Preconsolidation pressure vs. strain rate

然而需要说明的是，到目前为止，还没有可用的低应变速率（＜0.01%/h）和高应变速率（＞100%/h）下的试验结果，因此，在低和高应变速率范围内σp′与加载速率之间的关系如何（比如σp′是否存在极值），一直没有定论。究其原因，影响低加载速率下的CRS试验结果可能因素有：①用时过长，如应变速率为0.001%/h，达到体应变10%时，所需要的时间是417 d；②试验仪器位移控制台的加载速率精度控制问题（比如机械原因）；③试验时间过长，会造成土体自身产生温度/化学胶结。而且影响高加载速率下CRS试验结果可能因素有：①快速加载会引起孔压急剧产生，从而会导致试样中有效应力极不均匀；②快速加载过程中产生的声、热等能量消散问题，尚无法反映在有效应力理论中；③机械和设备原因，如传感器无法高速记录孔压变化等。这些因素都制约着低应变速率和高应变速率下黏土力学特性的研究。

2.1.2 压缩曲线的速率归一化

为探寻压缩曲线的速率归一化特性，Leroueil等[4]基于Batiscan黏土的14个CRS试验结果，把各CRS试验得到的压缩曲线（σv′-εv关系）用各自的先期固结压力σp′归一化，得到归一化后的各压缩曲线基本重合（图5(a)）。此外，作者[31]基于Vanttila黏土的3个固结试验（每级荷载历时分别为1、10、100 d）和7个CRS试验（加载速率范围1.11×10-6～1.11×10-5s-1）试验结果，同样得到归一化后的各压缩曲线基本重合（图5(b)）。此外，这种压缩曲线可以归一化的规律同样也得到了大量的其他 CRS试验的支持[4－9]，因此，可以得出结论：黏土的一维压缩曲线的速率相关性可由其先期固结压力σp′的应变率效应来表征，即可以用下式来表示：

式（2）也表明，先期固结压力σp′归一化的压缩曲线与加载速率无关。

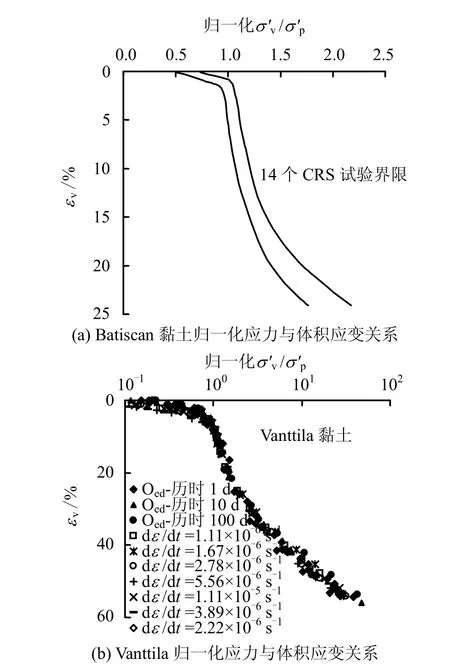
图5 黏土一维CRS试验归一化的应力-应变关系Fig.5 Normalized stress-strain relationships deduced from CRS tests

但需要说明的是，因为采用等时间线体系来描述土体的一维应变速率效应时（见图3(b)），不同应变率试验的应力从初始值增加到′过程中产生的弹性应变有差异，从而使得土体屈服时的应变不同，所以不同 CRS试验归一化的压缩曲线不会绝对重合。然而，式（2）并没有考虑应变率对屈服应变的这种影响。

2.1.3 不同先期固结压力-速率方程的探讨

（1）指数形式的速率方程

根据先期固结压力与加载速率对数间的线性关系，计算速率参数的速率方程可以统称为指数形式的速率方程。这些速率方程一般是在Graham等[9]所提方程基础上扩张而来，Graham等[9]最先用速率参数η0.1表达加载速率对先期固结压力的影响。η0.1表示以加载速率为0.1%/h的CRS试验对应的先期固结压力为基准值，当加载速率增大10倍时，先期固结压力的变化值与的比值表示为

基于此思想，更为通用的速率方程[15,33]可表示为

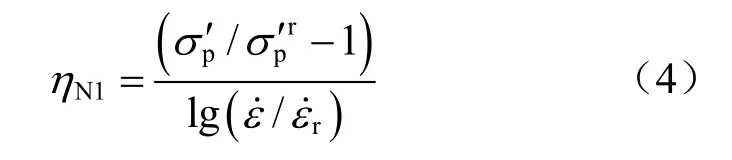
根据 Fodil等[34]的建议，另外一个速率方程可以表达为

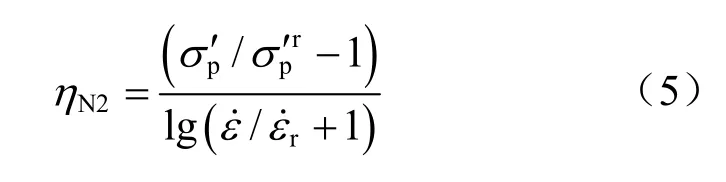
式（5）参数意义与式（4）相同，与式（4）的差别在于分母的速率比值加1；ηN2为速率参数。

（2）对数形式的速率方程

根据先期固结压力与加载速率双对数间的线性关系，学者们[35－37]提出了3种对数形式的速率方程，并得到了广泛应用[38－45]。

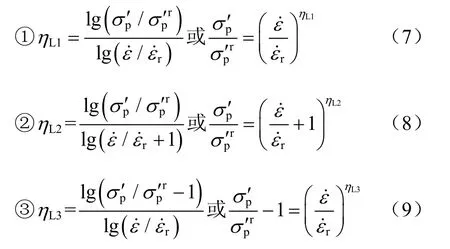
式中：ηL1、ηL2、ηL3为对数形式速率方程的速率参数[35－37]，其他参数的意义与方程（4）相同。

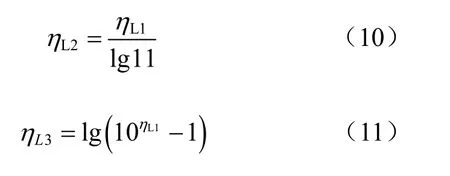
（3）各速率方程间的对比

为探讨上述速率方程（式（4）、（5）和式（7）～（9）的适用性，以Bastican黏土为例，图6(a)为先期固结压力′和加载速率关系，选用参照点处和为速率方程的参照值，5个速率方程的拟合结果分别见图6(b)～图6(e)。结果表明，用指数形式的速率方程式（4）和对数形式的速率方程式（7）拟合的结果回归系数R2最大，拟合结果最为理想。此外，式（5）、（8）需要在的基础上加1，使用不直接；而当小于′时，式（9）不再成立，因此式（9）有其特定的使用范围。因此，无论是从适用性还是拟合效果上来说，式（4）、（7）最有应用价值。

同样地，应用速率方程拟合了图4中所有黏土的先期固结压力加载速率效应，拟合出来的速率参数值、回归系数及土体物理特性见表 1。由所有土样的回归系数可知，式（4）、（7）最有应用价值。基于此，在下文中使用与式（4）、（7）对应的速率参数ηN1和ηL1来探讨软黏土的先期固结压力与加载速率效应特性。

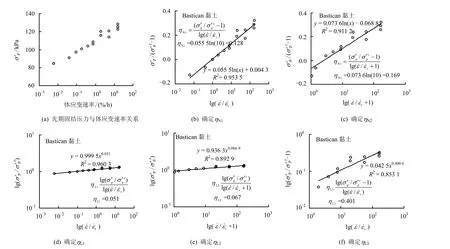
图6 先期固结压力-速率方程对比Fig.6 Comparison of preconsolidation pressure-rate formulations

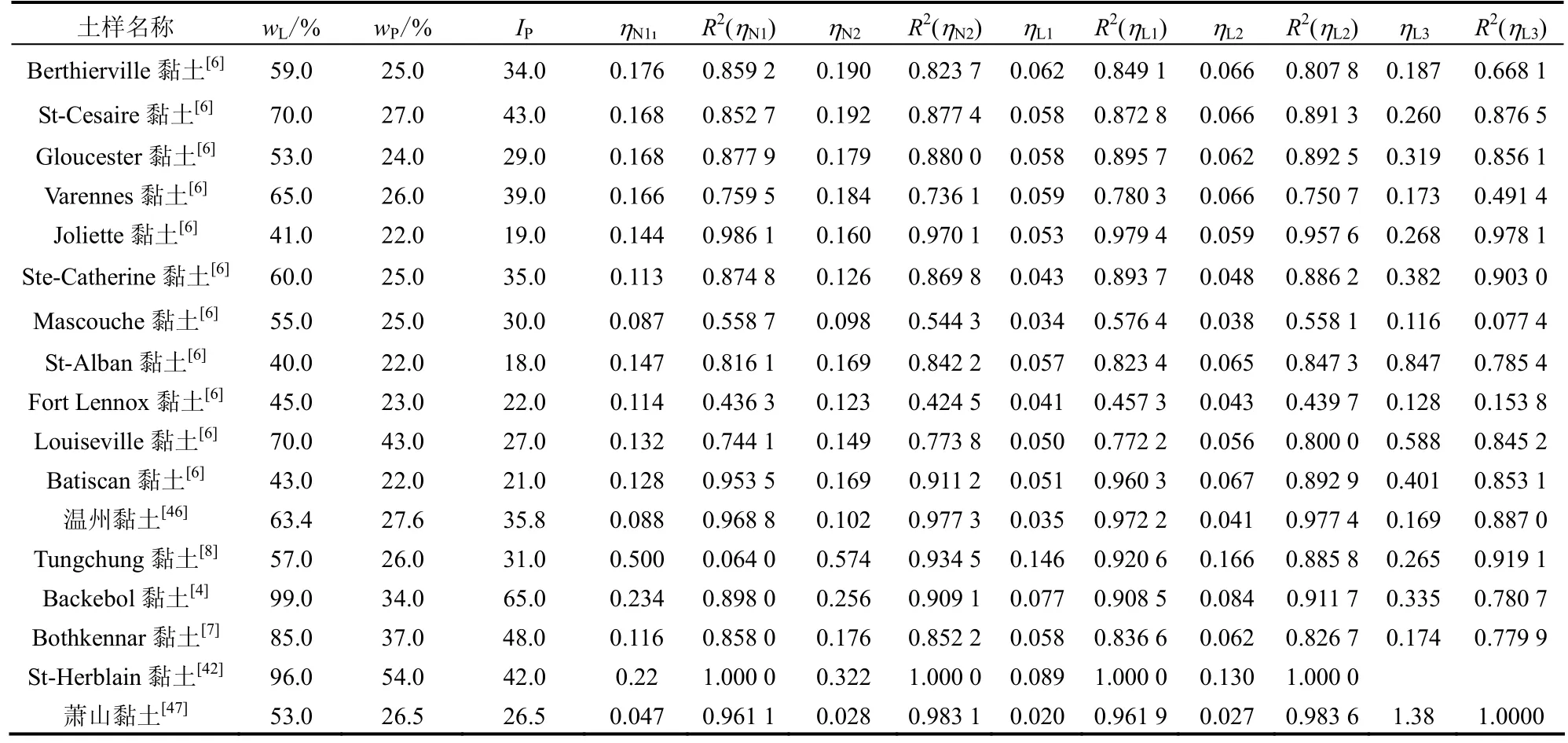
表1 一维CRS试验黏土物理特性及速率参数Table 1 Physical characteristics of 1D CRS test clays and rate parameters

按照 Casagrande塑性图分类（见图 7），图 4所调查的黏土包括低塑性无机黏土（CL）、高塑性无机黏土（CH）、高塑性粉质黏土和砂质黏土（OH）。为探寻速率参数值与土体黏塑性之间的关系，根据黏土在塑性图中的所处位置，统计出每个区域内所有黏土的速率参数ηN1和ηL1的最大、最小及平均值（见图7，去除了差异性太大的Tungchung黏土）。可以看出，塑性图中OH区的速率参数平均值最大，CH区次之，CL区最小。此外，绘制了速率参数ηN1和ηL1分别与液限（图8(a)）和塑性指数（图8(b)）关系图，并给出了线性拟合公式以及回归系数R2。结果表明，速率参数值与土的液限和塑性指数均有一定的线性规律，且从拟合效果上看，用液限拟合速率参数要优于塑性指数。

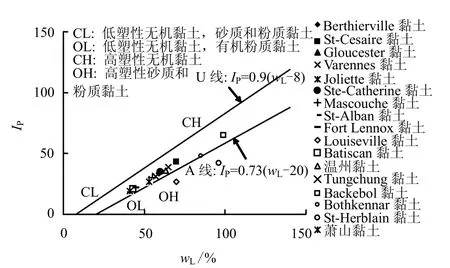
图7 一维CRS试验黏土在塑性图上的分类Fig.7 Classification of 1D CRS test soils in plasticity chart

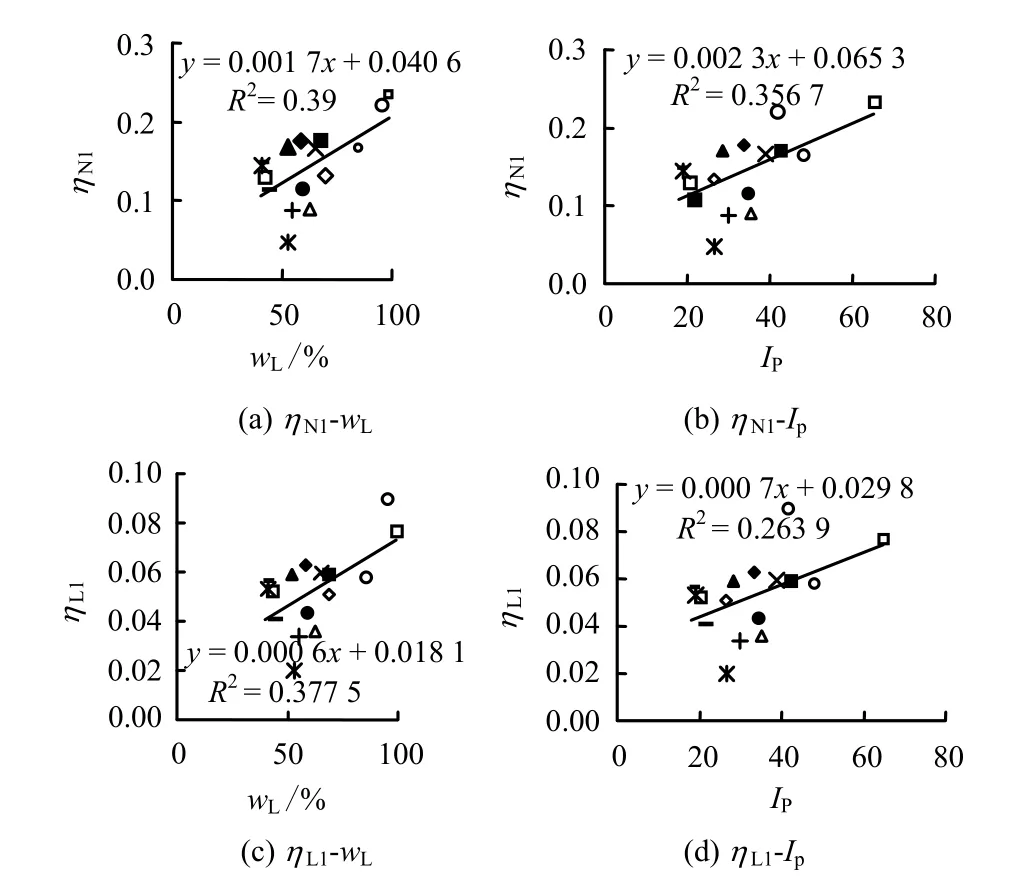
图8 η N1, η L1与 wL和 IP的关系Fig.8 Relationships between η N1, η L1 and wL, IP

此外，Mesri等[45]根据一维CRS试验与一维固结试验关系，提出先期固结压力和加载速率的关系与土样的次固结系数Cα及压缩指数Cc相关：

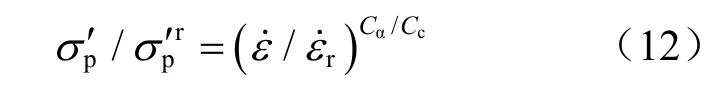
对比方程（7）、（12），不难发现：

而 Kutter等[40]、Leoni[41]、Yin[42]等认为下式更符合试验现象：

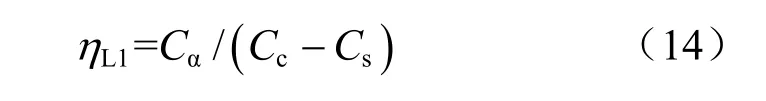
由于Cc通常是Cs的10倍左右，上述两个公式结果较为接近。由于文献中同时提供速率参数值和Cα/Cc值的结果较少，基于广泛黏土试验的速率参数值与次固结系数的相关性还有待于深入调查。

上述两种坐标系下的速率参数具有一定关联，联立方程（4）、（7），速率参数ηN1和ηL1的关系为

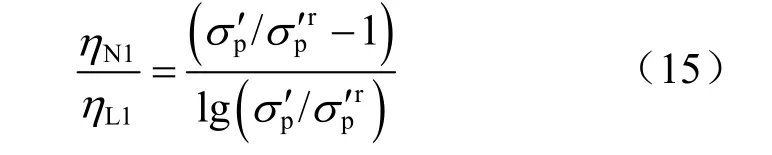
对于软黏土而言，比值 Cα/Cc的范围一般为0.030～0.090[48]。因此，ηL1的变化范围为 0.030～0.090，从而通过式（16）计算出ηN1的变化范围为0.072～0.230，这与表1所归纳黏土的速率参数ηN1和ηL1的变化范围基本吻合（ηL1为0.020～0.089，ηN1为0.047～0.234，去除了Tungchung黏土）。

2.2 三轴CRS试验

三轴 CRS试验就是在保持三轴压室围压力恒定的条件下，对试样通过竖向恒定位移速度控制施加荷载，在试验过程中直接测量竖向应力、孔隙水压力和竖向变形，进而得到三者之间的关系，以研究不同应变速率下土体抗剪特性。相对于一维CRS试验，土体三轴CRS试验可以通过控制试样侧向应力的大小，执行多种应力路径下的剪切试验，因此，研究三轴CRS试验特性也非常有必要。由于三轴排水试验要求低速率加载（低于0.18%/h以保证加载过程中土样内部不产生超孔隙水压力），不宜应用于速率效应的研究。因此，三轴CRS试验通常是在不排水条件下进行。类似于一维CRS试验，笔者基于现有三轴CRS试验结果，主要针对以下几个问题进行讨论：①不排水抗剪强度的速率效应；②应力-应变曲线的归一化；③不同抗剪强度-速率方程的探讨。

2.2.1 不排水抗剪强度的速率效应

由于不排水抗剪强度是评价黏土力学特性的一项重要指标，与工程设计与施工安全息息相关。Bjerrum[49]首次提出三轴不排水抗剪强度与加载速率相关的观点。然后，学者们通过大量的三轴CRS试验研究得出加载速率越大，土体的不排水抗剪强度越高，且应变率增加10倍时，土体不排水抗剪强度增长幅度大致在5%～20%之间的结论[15－18,50－55]。研究还表明，此增长幅度与土体固结状态（K0或等向固结）、固结应力及试验类型（伸长或压缩）均无关，而是与土体的物理力学性质相关。因此，土体物理力学性质的差异会导致不排水强度增长幅度不同。

为更形象地描述不排水抗剪强度 Su与应变速率的相关性，笔者总结了强度归一化的17种黏土的CRS试验结果。如图9所示，图中所有土样的应变速率在0.003～800%/h之间，在此应变速率范围内Su与加载速率呈正比关系。需要说明的是，因为在低应变速率（＜0.01%/h）和高应变速率（＞100%/h）下三轴CRS试验同样存在一维CRS试验可能存在的问题，因此，不排水抗剪强度Su与在两个极端应变速率范围内的规律如何，尚无法定论。

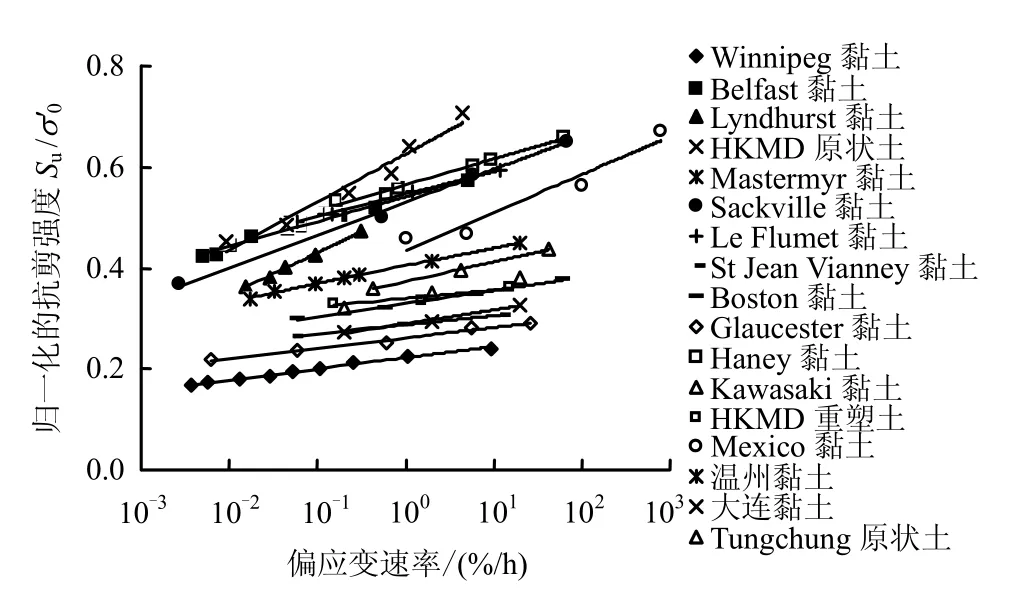
图9 不排水抗剪强度与应变速率关系Fig.9 Undrained shear strength vs. strain rate

2.2.2 应力-应变曲线的归一化

与一维CRS试验压缩曲线归一化特性类似，三轴 CRS试验同样具有应力-应变曲线的归一化特性[9]。不同的是，因为现有研究表明，三轴不排水抗剪强度峰值对应的应变与加载速率无关[14,18,56]，所以，理论上讲，三轴CRS试验归一化特性要优于一维CRS试验。以香港黏土在3种加载速率下的压缩与伸长试验为例，三轴压缩和伸长强度随加载速率增加逐渐增大（见图10(a)），且用与加载速率对应的最大压缩或伸长强度值归一化后的应力-应变曲线几乎重合（见图10(b)）。因此可以得出，不同加载速率下的三轴CRS试验应力-应变曲线具有较好的归一化特性。

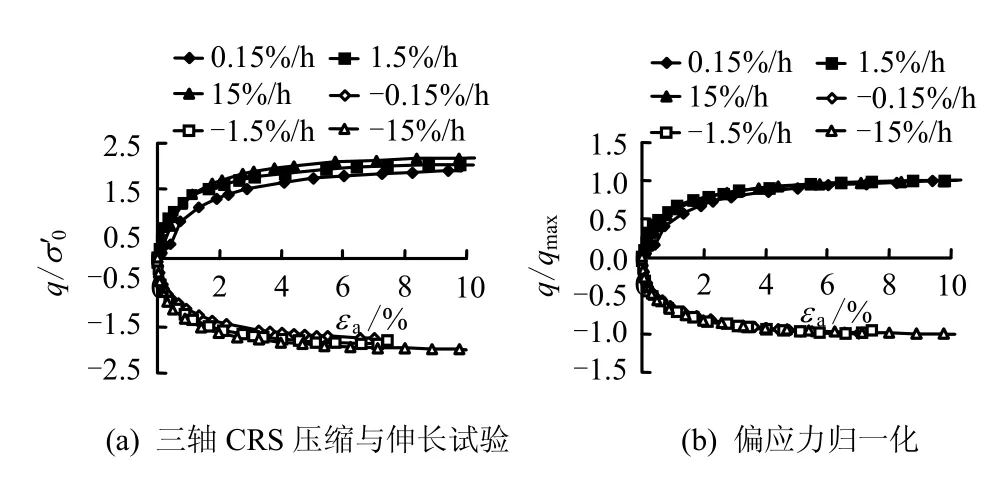
图10 三轴CRS压缩与伸长试验应力-应变曲线归一化Fig.10 Normalized stress-strain relationships for triaxial CRS compression and extension tests

2.2.3 不同抗剪强度-速率方程的探讨

综上所述，鉴于不排水抗剪强度在土力学研究中的重要性，研究其加载速率效应特性也很有意义。与一维CRS试验研究方法类似，在三轴CRS试验中同样采用速率参数值来表征加载速率对不排水抗剪强度的影响，且三轴CRS试验不排水抗剪强度的速率方程与一维 CRS试验先期固结压力的速率方程在表达式的形式上完全相同。采用类似的探讨方法，根据表达式形式的不同把速率方程分为两类：指数形式的速率方程和对数形式的速率方程。

指数形式的速率方程为

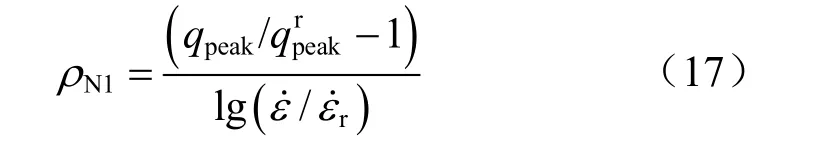
式中：qpeak为与应变率˙对应的峰值剪应力为与参考偏应变率对应的峰值剪应力；先期固结压力ρN1为速率参数；不排水抗剪强度Su= qpeak/2。

第2个指数形式的速率方程为

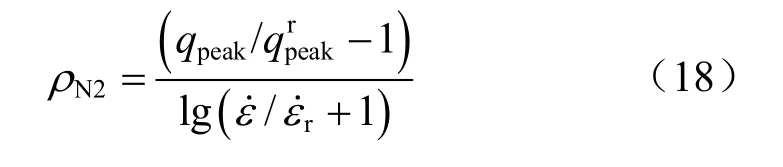
式（18）参数意义与式（17）的差别在于分母在速率比值的基础上加1；ρN2为速率参数。当10时，两个速率参数ρN1、ρN2之间的关系为

对数形式的速率方程：

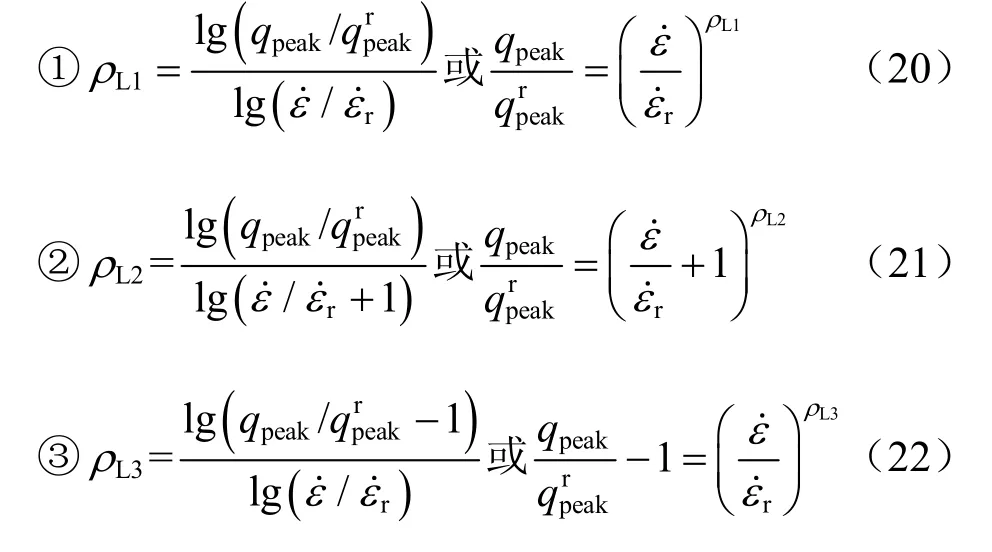
式中：ρL1、ρL2、ρL3为3个对数形式速率方程对于速率参数，其他参数的意义与方程（17）相同。且当时，3个速率参数ρL1、ρL2、ρL3之间的关系为

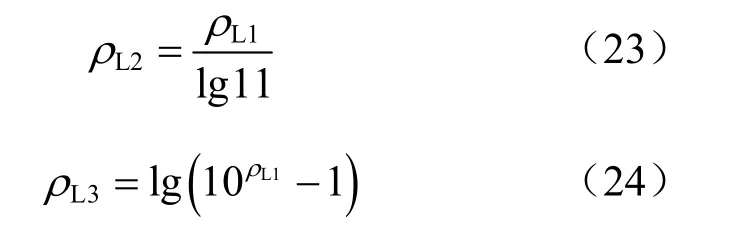
为探讨上述不排水抗剪强度速率方程（式（17）、（18）和式（20）～（22））的适用性，以Winnipeg黏土为例，图11(a)为不排水偏应力qpeak与加载速率关系，选用参照点处和为速率方程的参照值，5个速率方程的拟合结果分别见图 11(b)～图11(e)。结果表明，用指数形式的速率方程式（17）、（18）和对数形式的速率方程式（20）、（21）拟合的结果回归系数R2最大，拟合结果最为理想。此外，上文已述，式（18）、（21）需要在的基础上加1，使用起来也不直接，以及式（9）有其特定的使用范围综上所述，无论从适用性还是拟合效果上来说，式（17）、（20）最有使用价值。

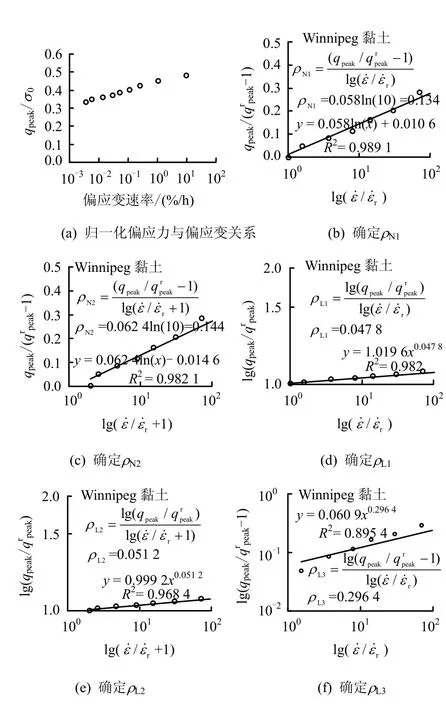
图11 三轴CRS试验不排水强度速率方程对比Fig.11 Comparison of rate formulation for triaxial undrained shear strength

同样地，应用速率方程拟合了图9中所有黏土的不排水抗剪强度加载速率效应，拟合出来的速率参数值、回归系数及土体物理特性见表 2。由所有土样的回归系数可知，式（17）、（20）最有应用价值。基于此，在下文中使用与式（17）、（20）对应的速率参数ρN1和ρL1来探讨软黏土的不排水抗剪强度加载速率效应特性。

按照Casagrande塑性图分类（图12），图9所调查的黏土同样包括低塑性无机黏土（CL）、高塑性无机黏土（CH）、高塑性粉质黏土和砂质黏土（OH）。根据黏土在塑性图中所处区域，统计区域内所有黏土速率参数值ρN1和ρL1（见表 2），得到了每个区域内速率参数最大、最小及平均值（见图12），可以看出，塑性图中CH区的速率参数平均值最大，OH区次之，CL区最小。此外，绘制了土的不排水抗剪强度速率参数值与土的液限和塑性指数关系，并给出了线性拟合公式以及回归系数R2。结果表明，土的不排水抗剪强度速率参数值与土的液限和塑性指数存在一定的线性规律。从拟合效果上看，速率参数ρN1与液塑限的相关性优于ρL1，且用塑性指数拟合速率参数值所对应的回归系数大于用液限的情况。

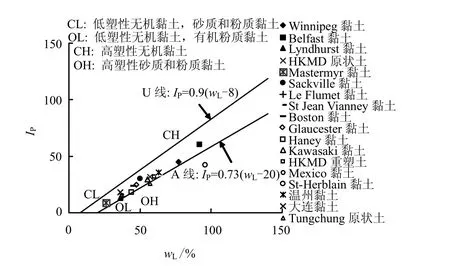
图12 三轴CRS试验黏土在塑性图上的分类Fig.12 Classification of 3D CRS test soils in plasticity chart

此外，根据式（17）、（20）可以推出ρN1和ρL1的关系：

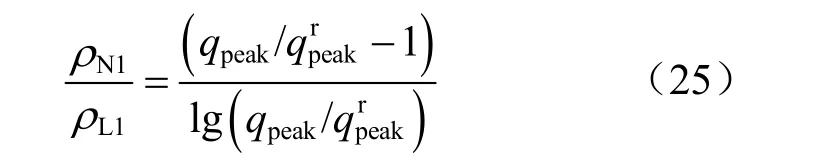
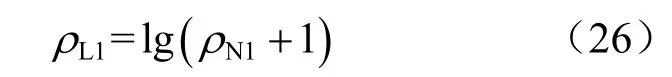
如前文所述，对于一般性软黏土，学者总结ρN1的范围为0.050～0.200，这与本文表2所归纳黏土的速率参数ρN1的变化范围基本一致，ρN1=0.055～0.230，ρL1=0.023～0.087。

2.3 复杂应力下实际土体CRS试验

实际工程中软黏土所受的应力状态远复杂于一维和三轴应力等理想土单元体状态[59－64]。因此，进行一些实际土体在复杂应力下的加载速率效应试验，如非常规室内试验等，也很有必要。

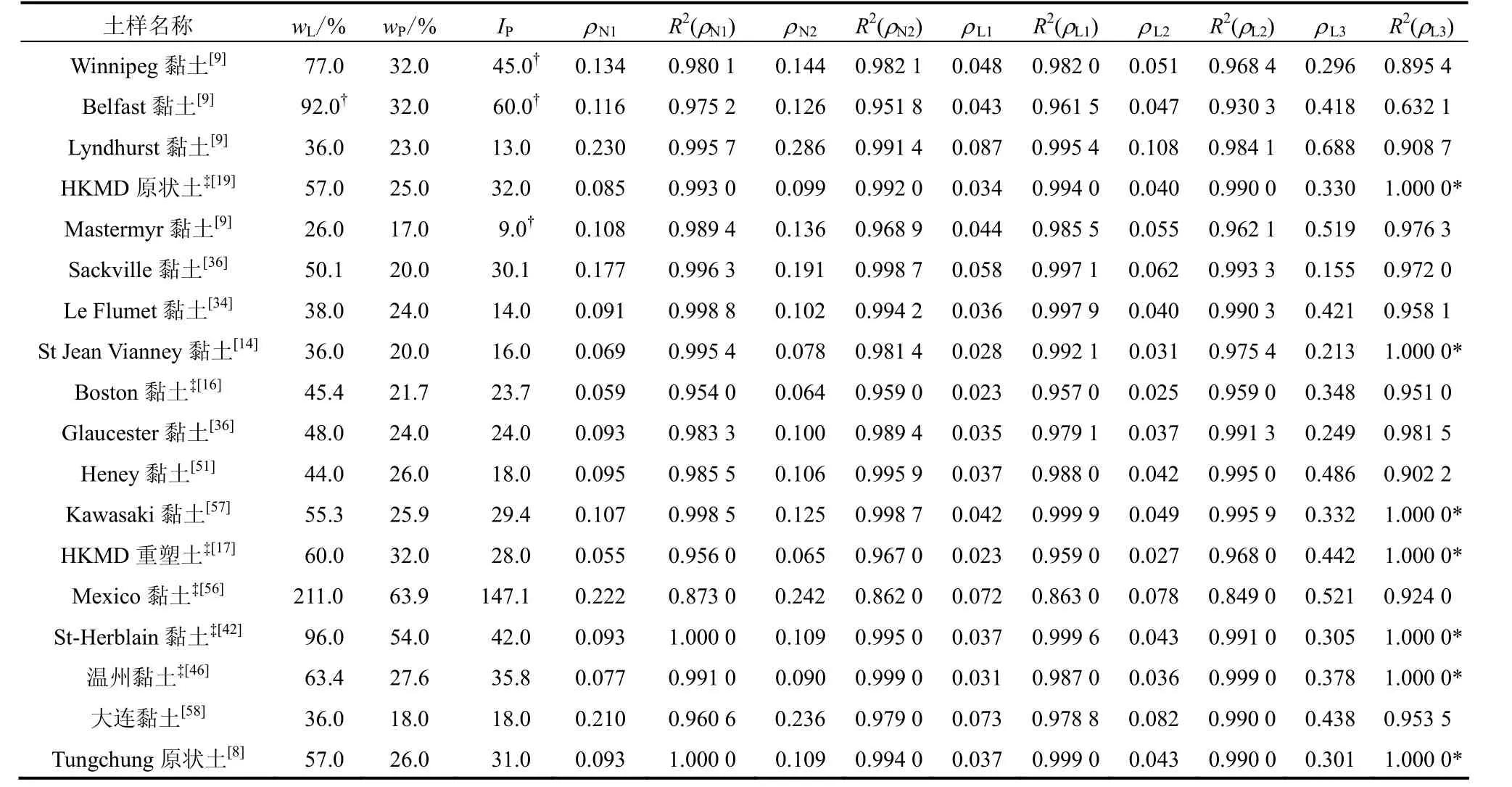
表2 三轴CRS试验黏土物理特性及速率参数Table 2 Physical characteristics of 3D test clays and rate parameters

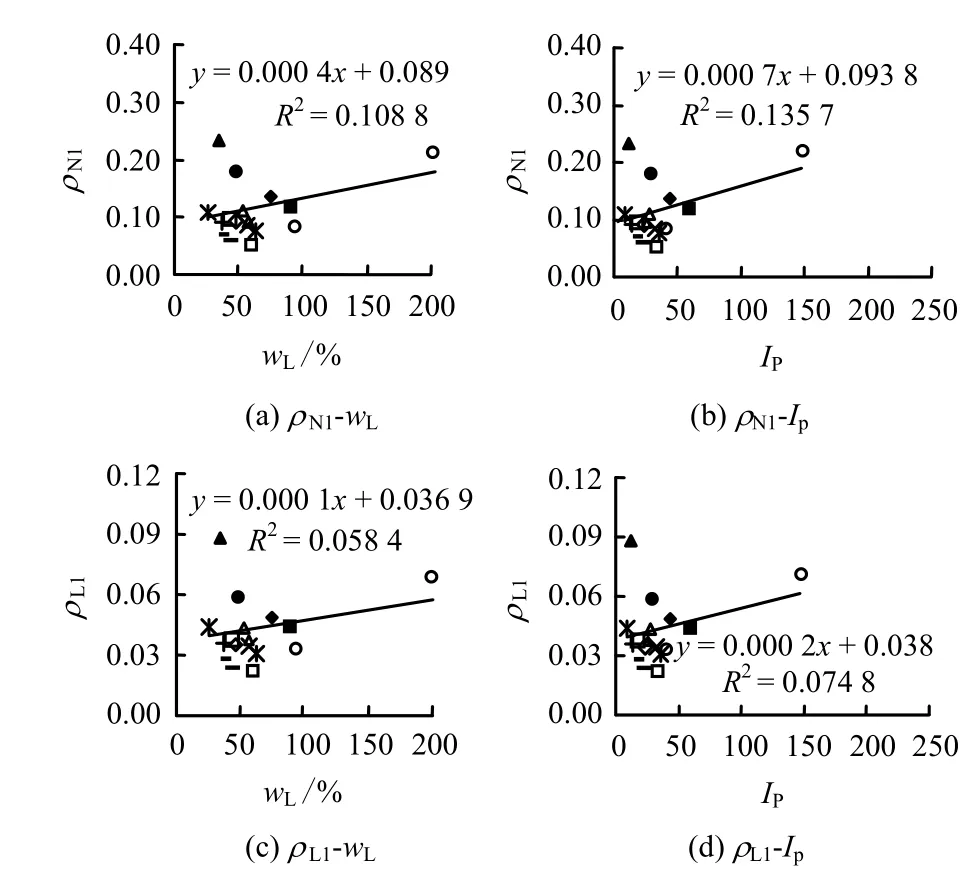
图13 ρ N1, ρ L1与 wL和 IP的关系Fig.13 Relationships between ρ N1, ρ L1 and wL, IP

十字板剪切试验作为一种快速测定饱和软黏土快剪强度的一种简易的原位测试方法，在我国沿海软土地区被广泛使用。Rangeard等[25]利用图14所示室内十字板剪切仪研究了剪切速率下的 Saint Herblain黏土抗剪强度的影响。试验在多级不同十字板旋转速度下进行，旋转速度依次为0.20、0.06、0.20、1.20 °/s，最大抗剪强度值出现在累计旋转角度20°～30°之间，归一化的剪切强度值与十字板旋转速度、累积旋转角度关系。很明显地，增大或减小十字板旋转速度会显著地引起抗剪强度值增加或降低。

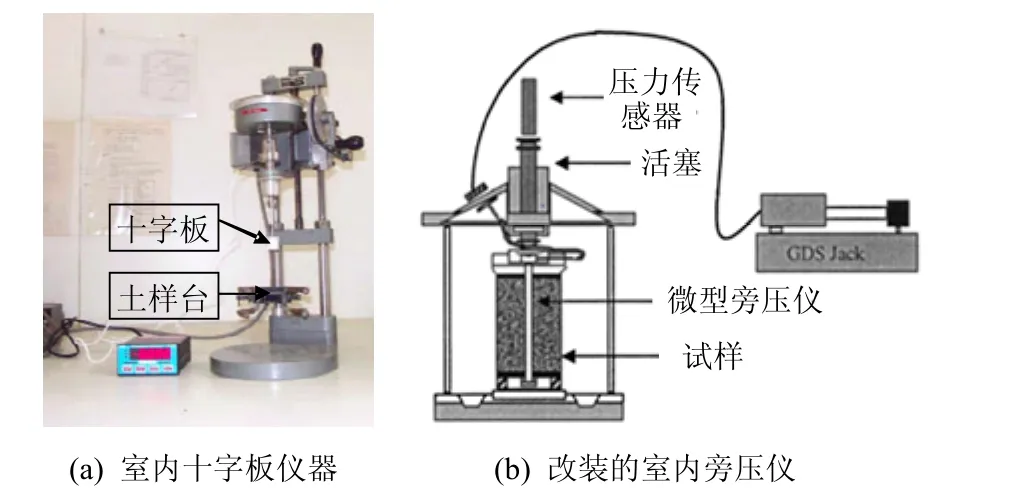
图14 室内十字板仪器[25]和改装的室内旁压仪[65]Fig.14 Laboratory vane shear apparatus and modified pressio-triax apparatus

另外，旁压仪也是一种能够方便测量土体应变速率效应的仪器。为了更有效地控制边界条件和土样均匀性，Hicher团队[25,65－66]开发了室内旁压测试仪（图14(b)）。Yin等[66]根据3个不同加载速率的旁压试验，利用反分析方法推演了黏土黏性参数，结合修正剑桥模型[67]优化了试验参数，并用实测值对该方法进行了验证，结果表明，利用旁压试验获得的参数值与三轴和固结试验值吻合。此外，Prevost[68]、Prapaharan 等[24]和 Silvestri[26]通过分析轴对称荷载作用下的小孔扩张理论，应用旁压试验推导了应变速率对土体不排水强度影响的解析解。

3 加载速率效应的统一性探讨

现有文献大都叙述软黏土加载速率效应的试验现象和一般性的研究方法，而没有具体描述黏土的速率参数特点以及讨论各CRS试验之间关系。本节尝试从以下3个方面进行加载速率效应的统一性探讨：①不排水抗剪强度速率效应与先期固结压力速率效应的统一性；②不排水抗剪强度的速率效应在三轴压缩与伸长条件下的统一性；③超固结度对不排水抗剪强度速率效应的影响。

3.1 一维-三轴统一性探讨

为探究一维和三轴加载速率效应之间的关系，作者选用温州原状土[15]作为研究对象，首先研究了一维先期固结压力（图15(a)）和三轴不排水抗剪强度与轴向应变速率关系（图15(b)），并以式（4）、（7）、（17）、（20）为例计算出加载速率参数ηN1=0.088、ηL1= 0.035、ρN1=0.077，ρL1=0.031（ρN1和ρL1为3个围压下的平均值）。然后，把一维先期固结压力和三轴不排水抗剪强度分别用加载速率为0.2%/h试验对应的强度值归一化，并绘于同一幅图（图15(c)）中。结果表明，温州黏土一维与三轴条件下的归一化强度值与轴向应变速率的对数近似呈直线关系。因此，可以说温州黏土在一维与三轴条件下的速率效应具有较好的统一性。

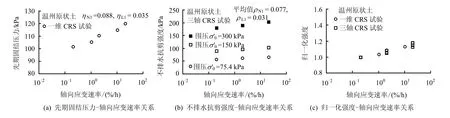
图15 温州黏土一维和三轴应变速率效应Fig.15 1D and 3D strain rate effect for Wenzhou clay

然而，对于St-Herblain黏土[42,65]和香港Tung Chung原状土[8]，其一维和三轴条件下的归一化强度差异性较大（见图16），速率效应不具有统一性。但需要注意的是，St-Herblain黏土的一维CRS试验只有两个加载速率下试验结果，由于原状土试验结果具有一定的离散型，因此，一维CRS试验条件下的速率参数值不具有统计意义；Tung Chung黏土的ηN1= 0.500，远高于本文所总结ηN1的一般变化范围（0.047～0.234），文献中缺乏原状土样不均匀性或其他原因的说明及探讨。

值得指出的是，对于同种黏土，同时做过一维CRS试验和三轴CRS试验的研究较少。因此，黏土的一维和三轴速率效应的统一性还需要更多的试验论证。

3.2 三轴压缩-伸长统一性探讨

实际工程中，有时土体会在压缩和伸长应力状态转换，如堆载、开挖等[69]，且施工速率会对黏土的压缩和伸长应力状态产生影响。因此，为了探究加载速率对三轴压缩和伸长特性影响的异同点，作者分析了温州原状土[15]、Mastemyr原状土[9]、香港重塑土[18]、香港原状土[19]和 Kawasaki重塑土[57]的不同加载速率下的三轴压缩和伸长试验。

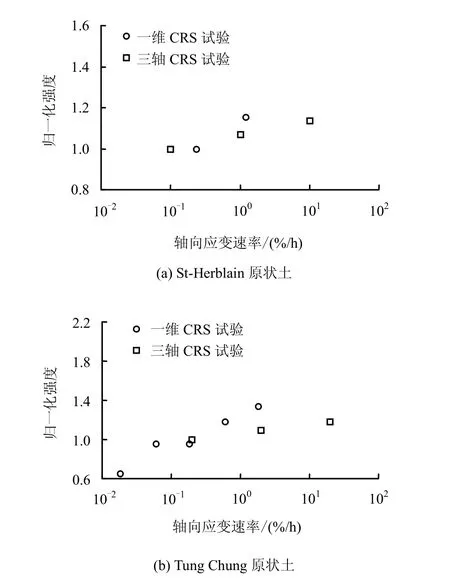
图16 St-Herblain和Tung Chung黏土一维和三轴应变速率效应Fig.16 1D and 3D strain rate effect for St-Herblain and Tung Chung clays

采用与上文相同的强度归一化方法，总结出各黏土三轴压缩和伸长条件下的归一化强度与轴向应变速率绝对值（伸长试验应变速率为负值）的对数关系（图17）。结果显示，温州黏土、Mastemyr黏土和香港原状土三轴压缩和伸长特性速率效应有较好的统一性；香港重塑土的三轴压缩和伸长特性速率效应有较大的差异性，可能与香港重塑土压缩试验ρN1= 0.049较低相关（本文总结ρN1的一般变化范围为0.055～0.229）；而由于Kawasaki重塑土伸长速率为42%/h的伸长强度值离散太大，造成ρN1=0.212，从而使得其三轴压缩与伸长特性速率效应的统一性较差。

综上所述，黏土三轴压缩与伸长特性的应变速率效应在总体上具有较好的统一性，但仍需更多的试验论证。

3.3 不同OCR统一性探讨

超固结土的力学特性研究同样是土力学研究中的重要课题。然而，在以往的试验中，同时考虑加载速率和 OCR对黏土不排水抗剪强度影响的试验较少，主要有香港重塑土[18]、Boston重塑土[16]及Mexico原状土[56]等试验研究。

采用与上文同样的研究方法分析这3种黏土，首先计算各OCR条件下的速率参数ρN1和ρL1，然后绘制归一化强度与轴向应变速率的关系图（见图18）。结果显示，Boston黏土和Mexico黏土在不同OCR条件下的加载速率效应统一性较差，而香港重塑土稍好。

因此，黏土的不同OCR条件下速率效应的统一性也需要更多的试验论证。

4 应力剪缩、剪胀的应变速率效应

应力剪缩、剪胀关系是土体的一个重要特性，也是研究土体本构关系的基础。众多学者研究了砂土的应力剪缩/剪胀关系[28]，而对黏土应力剪缩/剪胀特性的研究较少，尤其是加载速率对不同 OCR条件下三轴压缩与伸长过程中应力剪缩/剪胀特性的影响。本部分通过研究本文作者之一针对香港海相黏土的室内试验结果，探讨不同OCR，三轴压缩和伸长条件下黏土剪缩/剪胀的加载速率效应。

HKMD（香港海相沉积）软黏土基本的物理指标Gs=2.664，wP=28%，wL=60%，IP=32。试验前将所获得的天然沉积土经过制浆、过滤等过程，在竖向应力55 kPa下静置3周，制备成重塑土样。然后，进行了一系列不同OCR条件下的三轴CRS压缩和伸长试验[18, 70]。

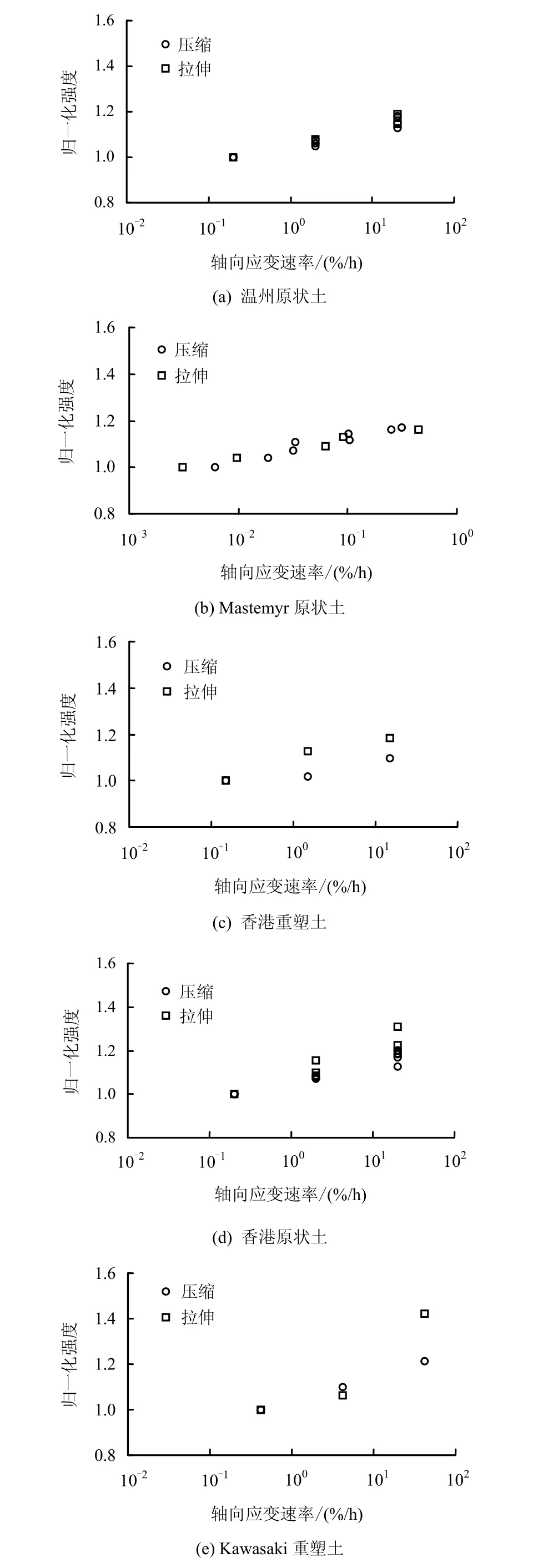
图17 归一化压缩与伸长强度值与轴向应变速率关系Fig.17 Normalized compression and extension strength vs. axial strain rate

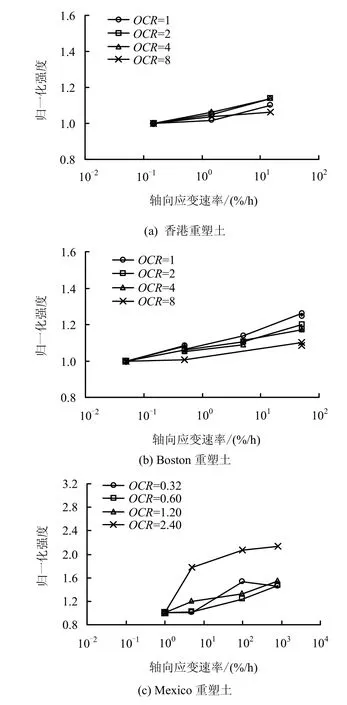
图18 不同OCR条件下归一化压缩强度值与应变速率关系Fig.18 Normalized compression strength vs. axial strain rate for different OCRs

不同超固结比（本试验中 OCR=1、2、4、8）三轴试样获取方法为：首先，在各向同性应力σo状态下对试样进行固结，三轴压缩和伸长试验试样固结持续时间分别为36 h和48 h；然后，卸载先期固结压力至与超固结比对应的围压值 σc=σo/OCR（表3），对于三轴压缩和伸长试验试样，此围压下的固结时间同样分别为36 h和48 h。另外，三轴CRS试验采用 3种加载速率加载，分别为±0.15、±1.5、±015%/h，符号“+”代表三轴压缩试验，符号“－”号代表三轴伸长试验。因此，对应于4种超固结比和3种加载速率下压缩与伸长试验，本试验方案共完成了24个三轴试验。试验过程中测量试样的孔隙水压力和轴向应力随轴向位移（时间）的发展关系。

4.1 三轴CRS试验非弹性应变增量

本部分阐述以OCR=1的试验为例。图19展示了OCR=1的香港海积黏土在三轴CRS压缩与伸长试验中归一化偏应力和孔隙水压力随轴向应变的变化规律，以及偏应力与平均有效应力的演变规律（CSL为临界状态线）。试验结果显示，无论压缩还是伸长试验，偏应力都会随着加载速率的增长而变大；在伸长试验中，随着轴向应变的发展，孔隙水压力在经历短暂的负压之后又变为正值，且逐渐增大。

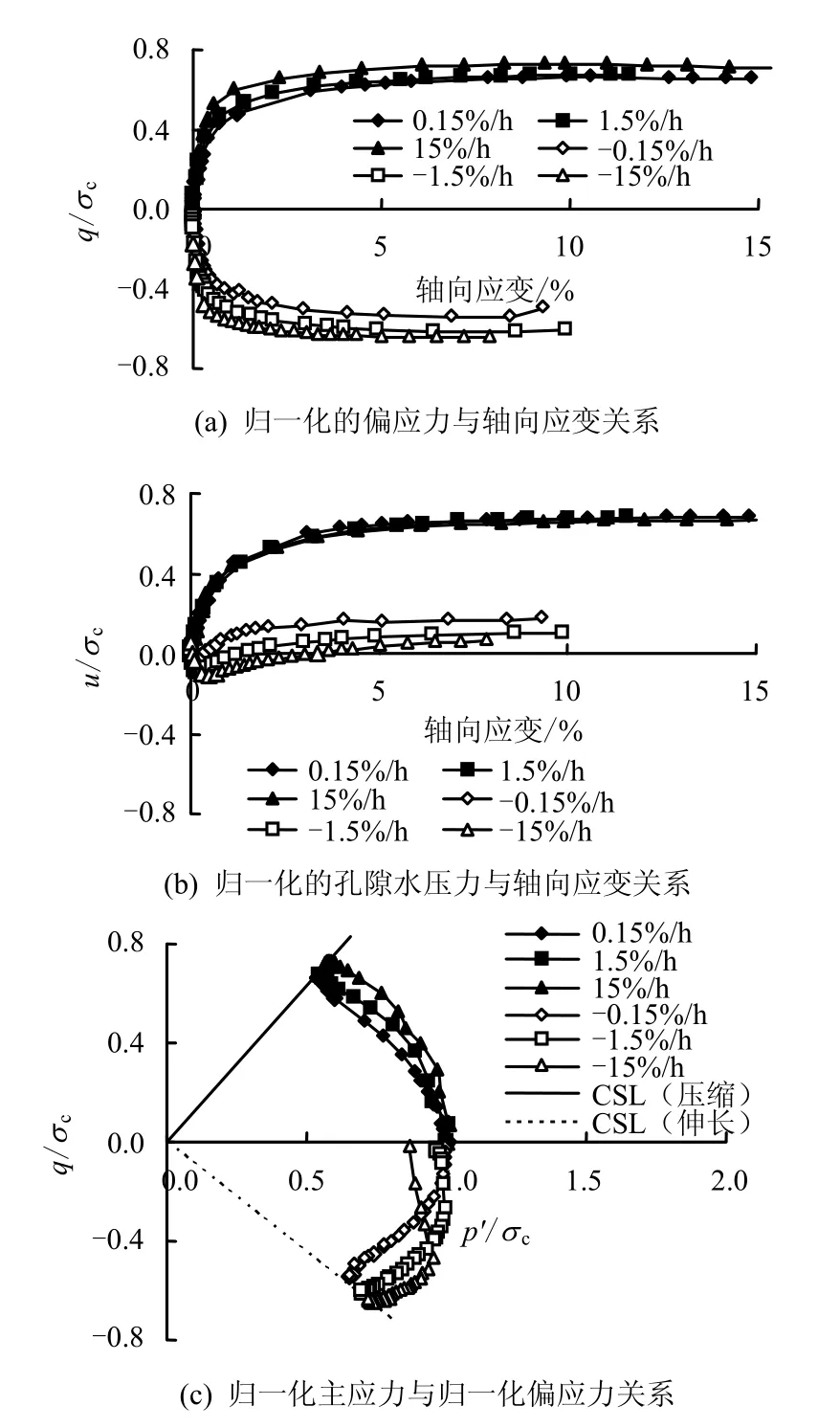
图19 香港海积黏土三轴CRS压缩与伸长试验（OCR=1）Fig.19 Triaxial CRS compression and extension tests of HKMD（OCR=1）

按照经典的弹塑性理论，总的体积应变增量和偏应变增量可以由两部分组成：弹性应变部分和非弹性应变部分（此处为塑性应变）：

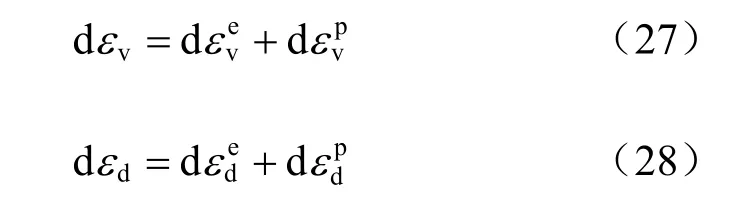
在三轴不排水试验中体应变为 0，所以塑性体积应变增量与弹性体积应变增量和为 0，即因此，可以通过平均有效应力增量计算塑性体积应变增量：

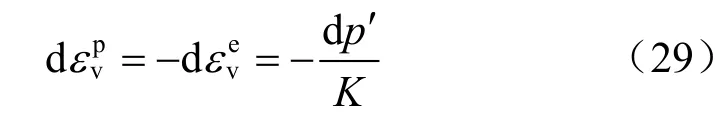
式中：体积模量 K=(1+e0)p′/κ，有效体应力 p′ =σc+q/3-u，κ为e-ln(p′)曲线中的回弹指数，u为孔隙水压力，q为偏应力。这样，即可以从图19得到塑性体积应变增量与应力比q/p′的关系（见图20(a)）。再则，因为不排水剪切过程中体应变为 0，即dεa+ 2dεr= 0，dεa为轴向应变增量，dεr为径向应变增量。因此，在不排水剪切过程中，可得到偏应变增量为

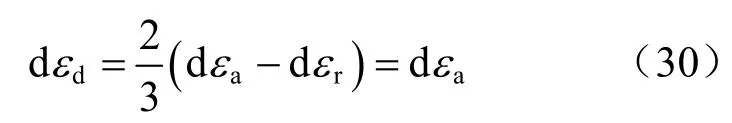
另外，方程（28）中的弹性偏应变增量可以通过偏应力增量dq计算：

剪切模量G可以通过体积模量和泊松比计算：

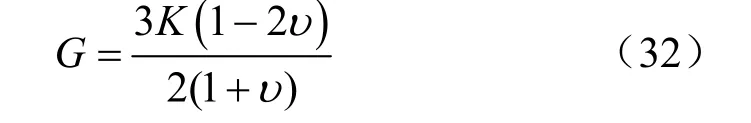
对于软黏土，泊松比一般取v = 0.2。因此，联合方程（28）、（30）、（32），塑性偏应变增量可以表达为

以此为基础，从图19得到塑性偏应变增量随应力比的变化规律（见图20(b)），从而可以得到塑性体积应变增量与塑性偏应变增量的比值随应力比的变化规律（见图20(c)）。

图20(a)表示：①压缩试验的塑性体积应变增量始终为正值；加载速率快的试验，其所产生的塑性体积应变增量越小，且达到最大值时对应的应力比越大。②而对于伸长试验，试验规律更复杂：加载速率为-0.15%/h的试验，塑性体积应变增量始终为正值，而其他两个伸长试验的塑性体积应变增量初始为负值，然后随着应力比的增长逐渐变为正值；加载速率快的试验，其所产生的塑性体积应变达到最大值时对应的应力比越大。图20(b)表示：①压缩试验的塑性偏应变增量为正值；加载速率慢的试验，其所产生的塑性偏应变增量始终大于加载速率快的试验。②伸长试验的塑性偏应变增量为负值；与压缩试验结果类似，加载速率慢的试验产生较大的塑性偏应变增量；应力比达到最大值时，塑性偏应变增量开始急剧增长。图20(c)表示，压缩试验和伸长试验都表现出剪缩特性，但从整体上来说，所选加载速率0.15～15%/h对压缩试验和伸长试验的应力剪缩/剪胀特性影响不大。

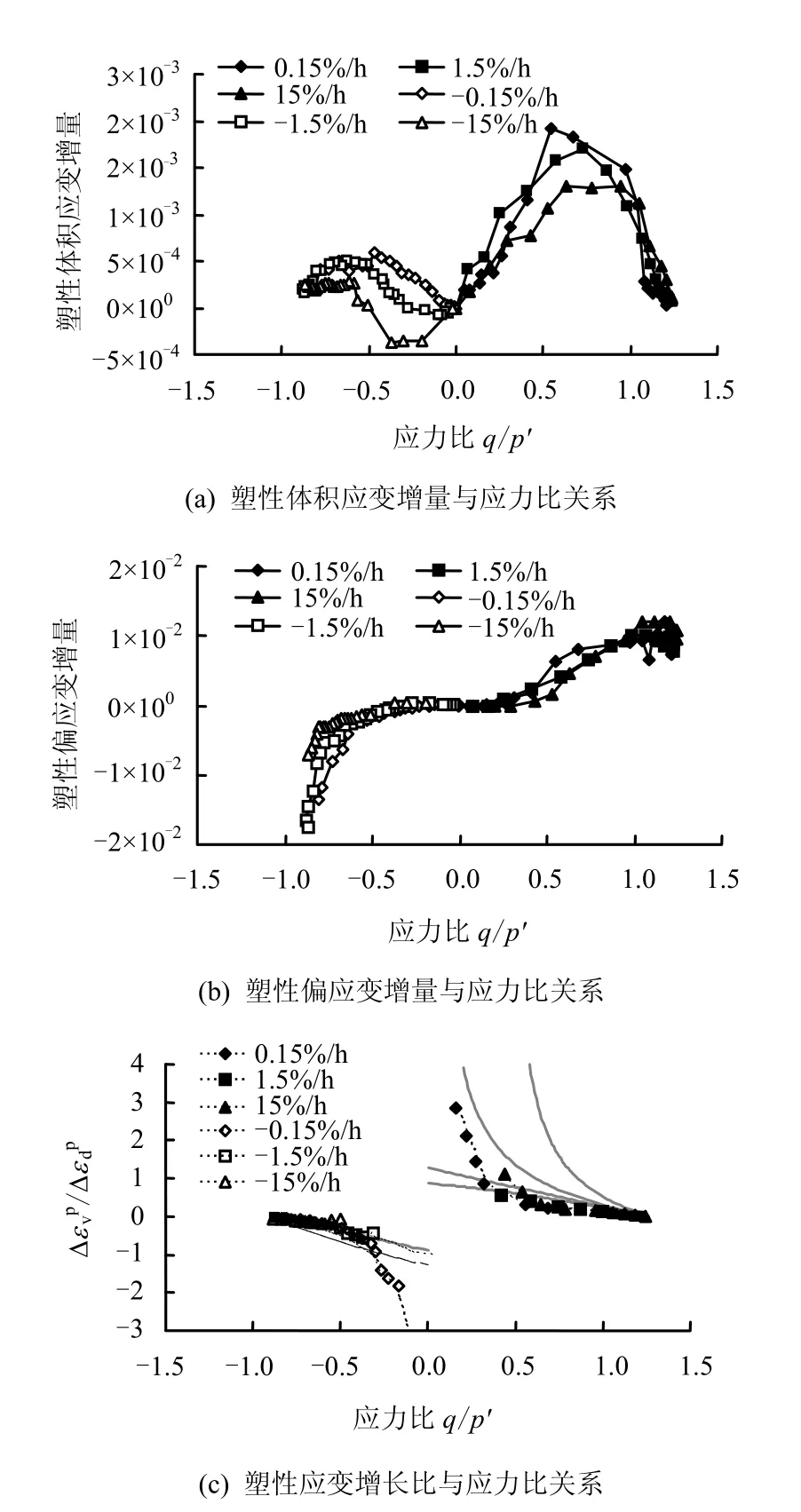
图20 塑性体积应变增量、塑性偏应变增量与应力比之间的关系Fig.20 Relationships of plastic volumetric strain increment,plastic deviatoric strain increment and stress ratio

用同样的方法，可以得到OCR分别为2、4和8的 HKMD 的应力剪缩/剪胀关系（见图 21(a)～图 21(c)）。结果显示：①3种 OCR条件下的 CRS伸长试验都表现出较强的剪胀特性，但速率规律性还不够明显；② OCR=2的压缩试验几乎无应力剪缩/剪胀，而OCR为4和8的压缩试验表现出应力剪胀特性，同样速率规律性不强。从这些结果可以得出，所选加载速率（0.15～15%/h）对不同超固结度黏土的应力剪缩/剪胀特性影响均不大。

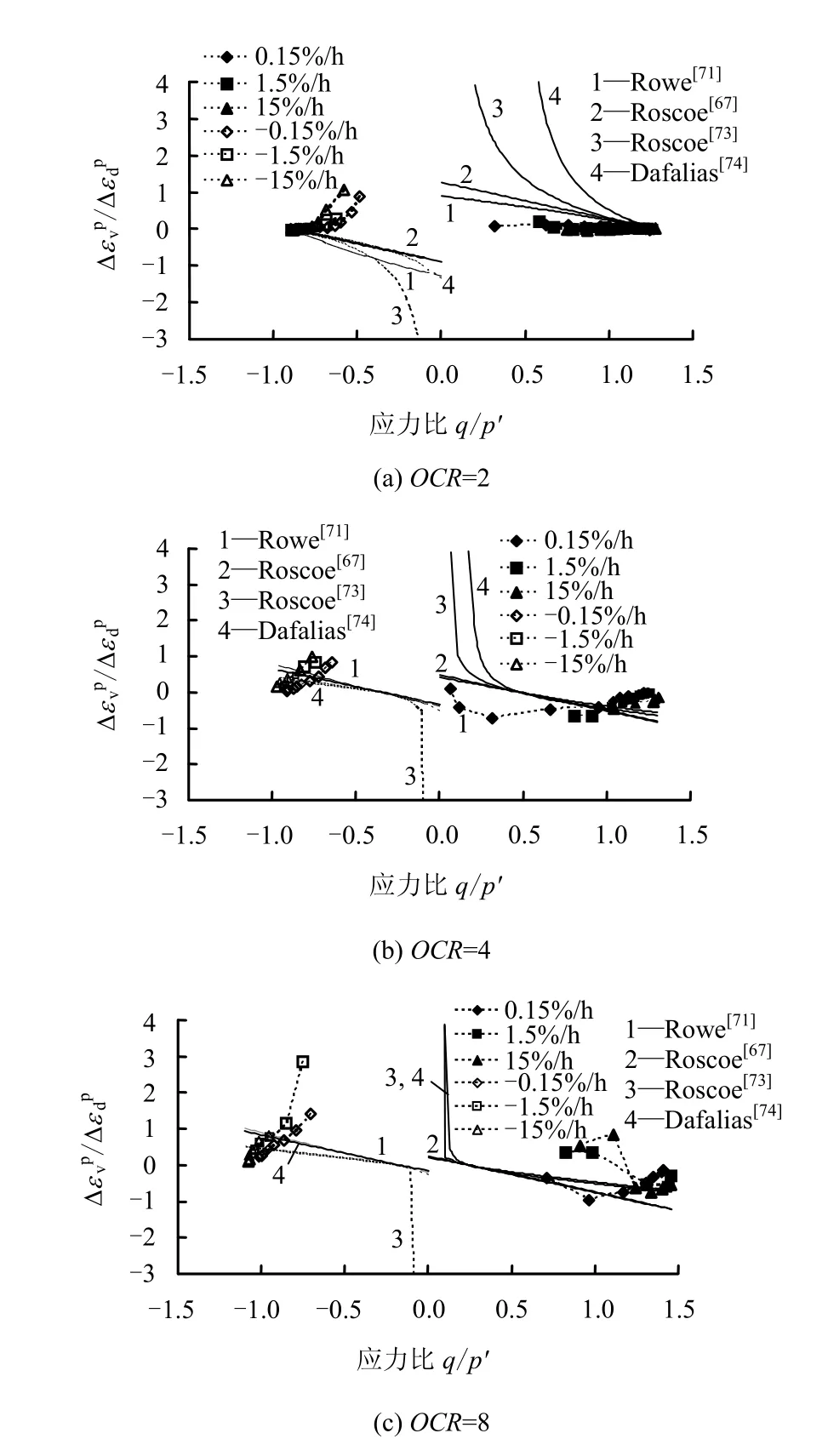
图21 OCR分别为2、4和8的HKMD的应力剪缩/剪胀关系Fig.21 Stress dilatancy of HKMD for OCRs=2, 4 and 8

因此，弹黏塑性理论可采用弹塑性理论中的应力剪缩/剪胀方程。下文中将首先介绍几种典型的应力剪缩/剪胀方程，然后评估其在拟合黏土压缩与伸长试验过程中的应力剪缩/剪胀特性的适用性。

4.2 几种典型的应力剪缩/剪胀方程

Reynolds在早期首先讨论了剪胀的物理表现，之后Rowe[71]和Roscoe等[67]引入了两种不同的剪胀方程，许多本构方程都是以这两种方程为基础建立的。Rowe[71]建立的应力剪胀方程假定输入能量增量与输出能量增量的比为恒定值 R。在压缩试验中，输入能量增量为，输出能量增量为而在伸长试验中，此两值相反。得到

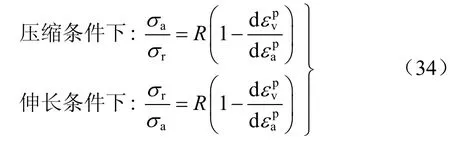
采用临界状态土力学中的变量，方程（34）可表示为

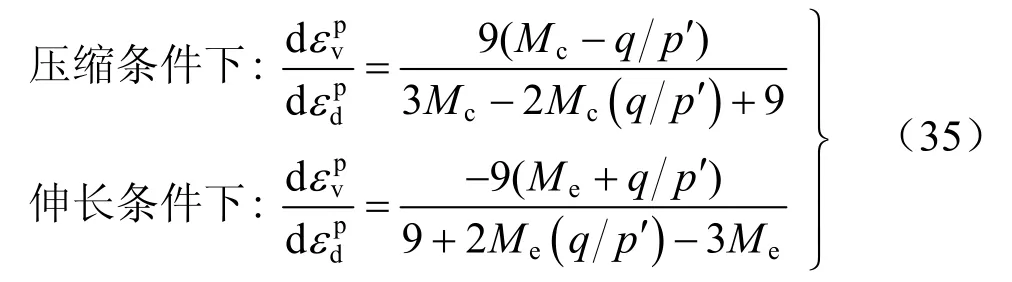
此外，Roscoe等[67]提出了一个基于三轴应力能量消散的剪胀方程，此方程表明，塑性增量与摩擦过程中消散的能量相等，得到

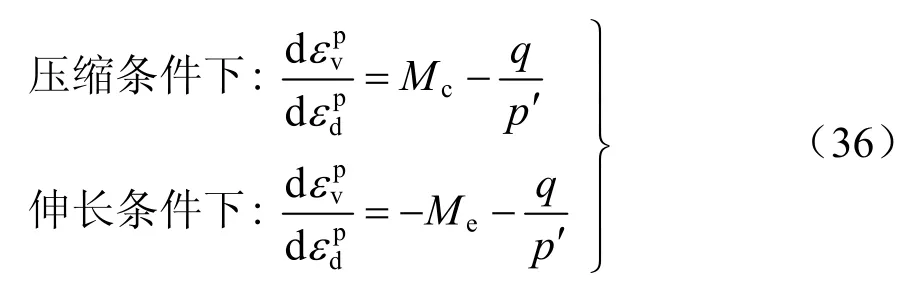
这个剪胀方程可以反映 Schofield等[72]所提出原始剑桥模型的流动法则。随着修正剑桥模型的发展，Roscoe等[73]提出了另一个被广泛使用的剪胀方程。此剪胀方程在三轴压缩与伸长应力状态下形式相同，可写为

基于此，在各向异性本构模型中，倾斜屈服面及塑性势面已被广泛接受[42,74－75]：

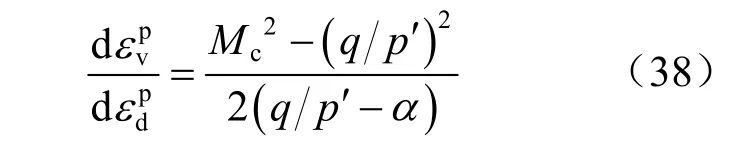
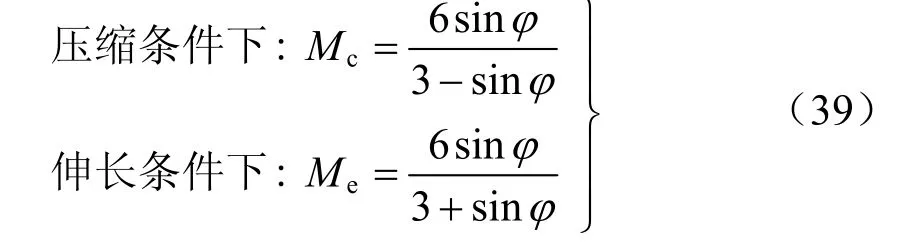
另外，因为当黏土的超固结比较高时（OCR＞2.5），在偏应力达到临界值前，就会产生剪缩/剪胀现象[76]。因此，为正确描述高 OCR条件下黏土的剪缩/剪胀现象，需要进一步修正方程（35）～（38）中的临界值。根据 Hattab等[76]超固结土剪缩/剪胀试验结果，得到归一化的 PT（状态转化，phase transformation）应力比与黏土超固结比的关系（见图22）。本文中正常固结HKMD黏土的Mc=1.27，Me=0.89，因此，当OCR=4方程（35）～（38）中的Mc=0.48，Me=0.34；而当OCR=8时，Mc=0.24，Me=0.14。

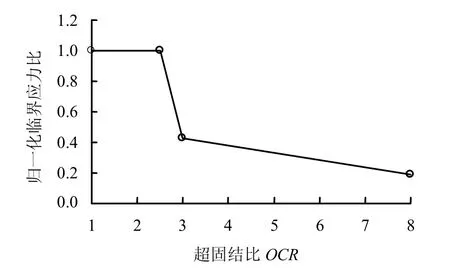
图22 归一化的临界应力比与超固结比关系Fig.21 Normalized critical stress ratio vs. OCR

将4种剪胀关系（式（35）～（38））绘于图20(c)和图21中，可以看出，在OCR=1时，Roscoe等[73]及 Dafalias[74]所提出的公式可以从总体趋势上描述三轴CRS压缩与伸长过程中的黏土应力剪缩特性。然而，当OCR分别为2、4和8时，无论对于压缩试验还是伸长试验，这4种剪胀方程都不能够很好地描述超固结黏土在三轴压缩与伸长过程中的黏土剪缩/剪胀特性。因此，对于超固结土，应引入密砂的动态PT应力比随应力状态而变化[27－28]，来改进各应力剪缩/剪胀方程。由于动态PT应力比难于显式表达[43]，这里暂不做修正。

5 结 论

（1）黏土的先期固结压力和不排水抗剪强度都具有应变速率效应，且应力-应变曲线具有归一化特性。本文总结黏土的速率参数ηL1的一般变化范围为0.020～0.089，ηN1为0.047～0.234，ρL1为0.055～0.230，ρN1为 0.023～0.087。

（2）针对先期固结压力与加载速率的关系，指数形式的速率方程（5）和对数形式的速率方程（7）适用性较强。同时，相同形式的速率方程（17）对黏土的不排水抗剪强度速率效应特性拟合效果较好，并建立了速率参数值与土的液塑性之间的关系。

（3）针对黏土强度加载速率效应的统一性，基于现有试验结果调查了一维和三轴条件、三轴压缩和伸长条件以及不同OCR条件，结果表明，黏土强度加载速率效应在各条件下具有一定的统一性，但还需要更多的试验论证。

（4）加载速率（0.15～15%/h）对不同条件下（压缩、伸长、不同 OCR）的黏土应力剪缩/剪胀特性影响不大。传统的剪缩/剪胀方程能较好地描述正常固结土的剪缩/剪胀关系，但对于超固结黏土则需要引入动态PT应力比来改进。

未来工作的重心将放在超低速及超高速加载试验仪器、方法及规律的研究上，速率效应与应力松弛及蠕变的相关性或等效性上，以期更全面、深入地认识效率效应机制，并为本构模型开发及工程应用提供必要的理论支持。

[1]BUISMAN A S. Results of long duration settlement tests[C]//Proceedings of 1st International Conference on Soil Mechanics and Foundation Engineering. Cambridge:[s. n.], 1936, 1: 103－107.

[2]KABBAJ M, TAVENAS F, LEROUEIL S. In-situ and laboratory stress-strain relationships[J]. Geotechnique,1988, 38(1): 83－100.

[3]HANZAWA H, TANAKA H. Normalized undrained strength of clay in the normally consolidated state and in the field[J]. Soils and Foundations, 1982, 32(1): 132－148.

[4]LEROUEIL S, KABBAJ M, TAVENAS F, et al.Stress–strain–strain rate relation for the compressibility of sensitive natural clays[J]. Géotechnique, 1985, 35(2):159－180.

[5]LEROUEIL S, KABBAJ M, TAVENAS F. Study of the validity of a σ′v-εv-dε/dt model in in-situ conditions[J].Soils and Foundations, 1988, 28(3): 13－25.

[6]LEROUEIL S, TAVENAS F, SAMSON L, et al.Preconsolidation pressure of Champlain clays (Part II):Laboratory determination[J]. Canadian Geotechnical Journal, 1983, 20(4): 803－816.

[7]NASH D F T, SILLS G C, DAVISON L R.One-dimensional consolidation testing of soft clay from Bothkennar[J]. Géotechnique, 1992, 42(2): 241－256.

[8]CHENG C, YIN J H. Strain-rate dependent stress-strain behavior of undisturbed Hong Kong marine deposits under oedometric and triaxial stress states[J]. Marine Georesources & Geotechnology, 2005, 23(1－2): 61－92.

[9]GRAHAM J, CROOKS J H A, BELL A L. Time effects on the stress-strain behaviour of natural soft clays[J].Géotechnique, 1983, 33(3): 327－340.

[10]YIN J H, GRAHAM J. Viscous-elastic-plastic modelling of one-dimensional time-dependent behaviour of clays[J].Canadian Geotechnical Journal, 1989, 26(2): 199－209.

[11]YIN Z Y, WANG J H. A one-dimensional strain-rate based model for soft structured clays[J]. Science China Technological Sciences, 2012, 55(1): 90－100.

[12]YIN Z Y, KARSTUNEN M. Modelling strain-ratedependency of natural soft clays combined with anisotropy and destructuration[J]. Acta Mechanica Solida Sinica, 2011, 24(3): 216－230.

[13]李建中, 彭芳乐, 龙冈文夫. 不同含水率黏土在不同试验条件下的应力-应变特性[J]. 岩土工程学报, 2006,28(3): 343－347.LI Jian-zhong, PENG Fang-le, TATSUOKA Fumio.Stress-strain behaviour of clay with different water contents under different test conditions[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(3): 343－347.

[14]VAID Y, ROBERTSON P K, CAMPANELLA R G. Strain rate behaviour of Saint-Jean-Vianney clay[J]. Canadian Geotechnical Journal, 1979, 16(1): 34－42.

[15]但汉波, 王立忠. K0固结软黏土的应变率效应研究[J].岩土工程学报, 2008, 30(5): 718－725.DAN Han-bo, WANG Li-zhong. Strain-rate dependent behaviors of K0consolidated clays[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(5): 718－725.

[16]SHEAHAN T C, LADD C C, GERMAINE J T.Rate-dependent undrained shear behavior of saturated clay[J]. Journal of Geotechnical Engineering, 1996,122(2): 99－108.

[17]ZHU J G, YIN J H, LUK S T. Time-dependent stress-strain behavior of soft Hong Kong marine deposits[J]. ASTM Geotechnical Testing Journal, 1999,22(2): 118－126.

[18]ZHU J G, YIN J H. Strain-rate-dependent stress-strain behavior of overconsolidated Hong Kong marine clay[J].Canadian Geotechnical Journal, 2000, 37(6): 1272－1282.

[19]YIN J H, CHENG C. Comparison of strain-rate dependent stress-strain behavior from K0-consolidated compression and extension tests on natural Hong Kong marine deposits[J]. Marine Georesources &Geotechnology, 2006, 24(2): 119－147.

[20]蔡羽, 孔令伟, 郭爱国, 等. 剪应变率对湛江强结构性黏土力学性状的影响[J]. 岩土力学, 2006, 27(8): 1235－1240.CAI Yu, KONG Ling-wei, GUO Ai-guo, et al. Effects of shear strain rate on mechanical behavior of Zhanjiang strong structured clay[J]. Rock and Soil Mechanics,2006, 27(8): 1235－1240.

[21]高彦斌, 汪中为. 应变速率对黏土非排水抗剪强度的影响[J]. 岩石力学与工程学报, 2005, 24(增刊2): 5779－5783.GAO Yan-bin, WANG Zhong-wei. Effect of strain rate on undrained shear strength of clays[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(Supp.2):5779－5783.

[22]CASAGRANDE A, WILSON S D. Effect of rate of loading on the strength of clays and shales at constant water content[J]. Géotechnique, 1951, 2(3): 251－263.

[23]YIN J H, ZHU J G, GRAHAM J. A new elastic viscoplastic model for time-dependent behaviour of normally and overconsolidated clays: theory and verification[J]. Canadian Geotechnical Journal, 2002,39(1): 157－173.

[24]PRAPAHARAN S, CHAMEAU J, HOLTZ R. Effect of strain rate on undrained strength derived from pressuremeter tests[J]. Geotechnique, 1989, 39(4): 615－624.

[25]RANGEARD D, HICHER P Y, ZENTAR R. Determining soil permeability from pressuremeter tests[J].International Journal for Numerical and Analytical Methods in Geomechanics, 2003, 27(1): 1－24.

[26]SILVESTRI V. Strain-rate effects in self-boring pressuremeter tests in clay[J]. Canadian Geotechnical Journal, 2006, 43(9): 915－927.

[27]CHANG C S, YIN Z Y. Modeling stress-dilatancy for sand under compression and extension loading conditions[J]. Journal of Engineering Mechanics, 2010,136(6): 777－786.

[28]YIN Z Y, CHANG C S. Stress-dilatancy behavior for sand under loading and unloading conditions[J].International Journal for Numerical and Analytical Methods in Geomechanics, 2011, doi:10.1002/nag.1125

[29]WANG L Z, YIN Z Y. Stress-dilatancy of natural soft clay under undrained creep condition[J]. International Journal of Geomechanics, 2012, doi:10.1061/(ASCE)GM 1943－5622.0000271

[30]ŠUKLJE L. The analysis of the consolidation process by the isotache method[C]//Proceedings of 4th International Conference on Soil Mechanics and Foundation Engineering. London: [s. n.], 1957, 1: 200－206.

[31]YIN Z Y, KARSTUNEN M, CHANG C S, et al.Modeling time-dependent behavior of soft sensitive clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(11): 1103－1113.

[32]YIN Z Y, KARSTUNEN M, HICHER P Y. Evaluation of the influence of elasto-viscoplastic scaling functions on modelling time-dependent behaviour of natural clays[J].Soils and Foundations, 2010, 50(2): 203－214.

[33]李建中, 彭芳乐. 描述黏土黏塑性的新参数[J]. 岩石力学与工程学报, 2005, 24(5): 859－863.LI Jian-zhong, PENG Fang-le. New parameter to describe viscoplastic property of clay[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(5): 859－863.

[34]FODIL A, ALOULOU W, HICHER P Y. Viscoplastic behaviour of soft clay[J]. Geotechique, 1997, 47(3): 581－591.

[35]ROWE R, HINCHBERGER S D. The significance of rate effects in modelling the Sackville test embankment[J].Canadian Geotechnical Journal, 1998, 35(3): 500－516.

[36]HINCHBERGER S D, ROWE R K. Evaluation of the predictive ability of two elastic-viscoplastic constitutive models[J]. Canadian Geotechnical Journal, 2005, 42(6):1675－1694.

[37]SHAHROUR I, MEIMON Y. Calculation of marine foundations subjected to repeated loads by means of the homogenization method[J]. Computers and Geotechnics,1995, 17(1): 93－106.

[38]LEROUEIL S, SOARES MARQUES M E. Importance of strain rate and temperature effects in geotechnical engineering[C]//Measuring and Modeling Time Dependent Soil Behavior. [S. l.]: [s. n.], 1996: 1－60.

[39]KIM Y, LEROUEIL S. Modeling the viscoplastic behaviour of clays during consolidation: application to Berthierville clay in both laboratory and field conditions[J]. Canadian Geotechnical Journal, 2001,38(3): 484－797.

[40]KUTTER B L, SATHIALINGAM N. Elastic viscoplastic modelling of the rate-dependent behaviour of clays[J].Geotechnique, 1992, 42(3): 427－441.

[41]LEONI M, KARSTUNEN M, VERMEER P A.Anisotropic creep model for soft soils[J]. Géotechnique,2008, 58(3): 215－226.

[42]YIN Z Y, CHANG C S, KARSTUNEN M, et al. An anisotropic elastic-viscoplastic model for soft clays[J].International Journal of Solids and Structures, 2010,47(5): 665－677.

[43]YIN Z Y, HATTAB M, HICHER P Y. Multiscale modeling of a sensitive marine clay[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35(15): 1682－1702.

[44]尹振宇. 天然软黏土的弹黏塑性本构模型：进展及发展[J]. 岩土工程学报, 2011, 33(9): 1357－1369.YIN Zhen-yu. Elastic viscoplastic models for natural soft clay: review and development[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(9): 1357－1369.

[45]MESRI G, CHOI Y K. Strain rate behaviour of Saint Jean Vianney clay: Discussion[J]. Canadian Geotechnical Journal, 1979, 16(4): 831－834.

[46]但汉波. 天然软黏土的流变特性[博士学位论文 D]. 杭州: 浙江大学, 2008.

[47]齐添. 软土一维非线性固结理论与试验对比研究[博士学位论文D]. 杭州: 浙江大学, 2008.

[48]MESRI G, GODLEWSKI P. Time and stress compressibility interrelationship[J]. Journal of the Geotechnical Engineering Division, 1977, 103(5): 417－430.

[49]BJERRUM L. Engineering geology of Norwegian normally-consolidated marine clays as related to settlements of buildings[J]. Géotechnique, 1967, 17(2):83－118.

[50]TAVENAS F, LEROUEIL S, LA ROCHELLE, et al.Creep behaviour of an undisturbed lightly overconsolidated clay[J]. Canadian Geotechnical Journal, 1978, 15(3): 402－423.

[51]VAID Y P, CAMPANELLA R G. Time-dependent behavior of undisturbed clay[J]. Journal of the Geotechnical Engineering Division, 1977, 103(7): 693－709.

[52]LEFEBVRE G, LEBOEUF D. Rate effects and cyclic loading of sensitive clays[J]. Journal of Geotechnical Engineering, 1987, 113(5): 476－489.

[53]KULHAWY F H, MAYNE P W. Manual on estimating soil properties for foundation design[M]. New York:Cornell University, 1990.

[54]RICHARDSON A M, WHITMAN R V. Effect of strain-rate upon undrained shear resistance of a saturated remoulded fat clay[J]. Géotechnique, 1963, 13(4): 310－324.

[55]SORENSEN K K, BAUDET B A, SIMPSON B.Discussion: Influence of structure on the time-dependent behaviour of a stiff sedimentary clay[J]. Géotechnique,2007, 57(9): 783－787.

[56]DÍAZ-RODRíGUEZ J A, MARTíNEZ-VASQUEZ J J,CARLOS SANTAMARINA J. Strain-rate effects in Mexico City soil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(2): 300－305.

[57]NAKASE A, KAMEI T. Influence of strain rate on undrained shear characteristics of K0-consolidated cohesive soils[J]. Soils and Foundations, 1986, 26(1): 85－95.

[58]齐剑锋, 栾茂田, 聂影, 等. 饱和黏土剪切变形与强度特性试验研究[J]. 大连理工大学学报, 2008, 48(4): 551－556.QI Jian-feng, LUAN Mao-tian, NIE Ying, et al.Experimental study of shear and strength behavior of saturated clay[J]. Journal of Dalian University of Technology, 2008, 48(4): 551－556.

[59]尹振宇, 张冬梅, HICHER P Y, 等. 一个能够模拟软土时效特性的简单弹黏塑性模型[J]. 岩土工程学报, 2008,30(6): 880－888.YIN Zhen-yu, ZHANG Dong-mei, HICHER P Y, et al.Modeling of the time-dependent behavior of soft soils using a simple elasto-viscoplastic model[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(6): 880－888.

[60]尹振宇, 黄宏伟, UTILI S, 等. 模拟堤坝荷载作用下软土的速率效应特性[J]. 岩土工程学报, 2009, 31(1): 109－117.YIN Zhen-yu, HUANG Hong-wei, UTILI S, et al.Modeling rate-dependent behavior of soft subsoil under embankment loading[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(1): 109－117.

[61]KARSTUNEN M, YIN Z Y. Modelling time dependent behaviour of Murro test embankment[J]. Géotechnique,2010, 60(10): 735－749.

[62]YIN Z Y, KARSTUNEN M, WANG J H, et al. Influence of features of natural soft clay on the behavior of embankment[J]. Journal of Central South University of Technology, 2011, 18(5): 1667－1676.

[63]YIN Z Y, XU Q, YU C. Elastic viscoplastic modeling for natural soft clays considering nonlinear creep[J].International Journal of Geomechanics, 2012, doi:10.1061/(ASCE)GM.1943－5622.0000284

[64]KARSTUNEN M, REZANIA M, SIVASITHAMPARAM N, et al. Comparison of anisotropic rate-dependent models for modelling consolidation of soft slays[J].International Journal of Geomechanics, 2012,doi:10.1061/(ASCE)GM.1943－5622.0000267

[65]YIN Z Y. Modélisation viscoplastique des argiles naturelles et application au calcul de remblais sur sols compressibles[D]. [S. l.]: Ecole Centrale de Nantes, 2006.

[66]YIN Z Y, HICHER P Y. Identifying parameters controlling soil delayed behaviour from laboratory and in-situ pressuremeter testing[J]. International Journal for Numerical Methods in Geomechanics, 2008, 32(12):1515－1535.

[67]ROSCOE K H, SCHOFIELD A N, THURAIRAJAH A.Yielding of clays in states wetter than critical[J].Geotechnique, 1963, 13(3): 211－240.

[68]PREVOST J H. Undrained stress-strain-time behavior of clays[J]. Journal of the Geotechnical Engineering Division, 1976, 102(12): 1245－1259.

[69]WANG L Z, SHEN K L, YE S H. Undrained shear strength of K0consolidated soft soils[J]. International Journal of Geomechanics, 2008, 8(2): 105－113.

[70]朱俊高. 土体的流变特性与弹黏塑性模拟[M]. 北京:科学出版社, 2007.

[71]ROWE P W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact[C]//Proceedings of the Royal Society A: Mathematical,Physical and Engineering Sciences. [S. l.]: [s. n.], 1962,269: 500－527.

[72]SCHOFIELD A N, WROTH P. Critical state soil mechanics[M]. London: McGraw-Hill, 1968.

[73]ROSCOE K H, BURLAND J B. On the generalized stress-strain behaviour of wet clay: Engineering plasticity[M]. Cambridge: Cambridge University Press,1968: 535－609.

[74]DAFALIAS Y F. Anisotropic critical state clay plasticity model[C]//Proceedings of the 2nd International Conference on Constitutive Laws for Engineering Materials. [S. l.]: Tucson Elsevier, 1987, 1: 513－521.

[75]WHEELER S J, NÄÄTÄNEN A, KARSTUNEN M, et al.An anisotropic elastoplastic model for soft clays[J].Canadian Geotechnical Journal, 2003, 40(2): 403－418.

[76]HATTAB M, HICHER P Y. Dilating behaviour of overconsolidated clay[J]. Soils and Foundations, 2004,44(4): 27－40.