单层非饱和多孔介质一维瞬态响应半解析解

凌道盛 ，王 筠 ，单振东，丁皓江

（1. 浙江大学 软弱土与环境土工教育部重点实验室，杭州 310058；2. 浙江大学 岩土工程研究所，杭州 310058；3. 中国地震局工程力学研究所，哈尔滨 150080）

1 引 言

多孔介质瞬态响应问题的研究是岩土工程、地震工程和地球物理等学科领域的一个重要课题。在岩土工程中，如果多孔介质内充满单一流体，则称这种多孔介质是饱和的；如果多孔介质内存在多种流体，则称这种多孔介质是非饱和的[1]。大多数情况下，多孔介质内有两种流体共存。它们可能是两种液体，如石油工程中的油和水；也可能是一种液体和一种气体，如非饱和土中的水和气。

自从Biot[2－3]1956年建立饱和多孔介质波动理论以来，多孔介质的波动理论引起了包括岩土工程在内的多个领域的学者的广泛重视。由于存在惯性、黏性和机械耦合作用，多孔介质的动力问题比单相弹性介质复杂得多，大多数问题只能通过时间和空间上离散等数值方法进行求解，即使是一维的瞬态响应问题，也只能在某些特殊情形下才能给出解析解。Garg等[4]运用Laplace变换法求解一维瞬态响应问题，得到了黏性耦合作用为0或无穷大两种极端情况下时域内的解析解；Simon等[5]运用Laplace变换给出了材料参数满足动力相容条件时的解析解；Gajo等[6]给出了分离变量型的位移通解和饱和多孔介质层上下表面同时作用阶跃位移的精确解；Schanz等[7]运用 Laplace变换给出了黏性耦合为 0时的解析解；凌道盛等[8]给出了单层不可压缩饱和多孔介质一维瞬态响应的精确解；Shan等[9]运用分离变量法给出了3类非齐次边界条件的精确解；凌道盛等[10]提出了一种适用于单层饱和多孔介质任意非齐次边界条件的半解析方法。

针对非饱和多孔介质一维瞬态响应问题的研究成果相对较少，Li等[11]基于混合物理论，运用Laplace变换研究了单层问题，给出了变换域内的解析解和时域内的数值Laplace逆变换解；Shan等[12]给出了单层问题3类典型非混合边界条件的级数解和半无限问题两类边界条件的积分解。1964年Brutsaert[13]指出，非饱和多孔介质内存在3种类型的压缩波，这与饱和多孔介质（两类压缩波）存在显著的不同，深入认识非饱和多孔介质一维瞬态响应是理解多孔介质内波动传播的基础，有必要对非饱和多孔介质一维瞬态响应问题开展进一步的研究。

综上可见，针对非饱和多孔介质的一维瞬态响应问题的研究还比较少，目前还没有适用混合边界的解析解，而且基于 Laplace变换法的求解方法存在数值 Laplace逆变换稳定性较差、在响应时间较长时可能出现发散等不足[14]。本文以一类混合边界条件为例，给出了一种考虑孔隙流体和固体颗粒压缩性以及惯性、黏滞和机械耦合作用的半解析解法。该解法不受边界条件和材料参数的限制，具有很好的适用性。

2 基本方程和定解条件

本文研究的一维单层非饱和多孔介质及其坐标系如图1所示。图中，H为非饱和多孔介质层厚度。

2.1 基本方程

Zienkiewicz 等[15]和 Li等[16]将 Biot理论[2－3]推广到非饱和多孔介质领域，提出了非饱和多孔介质波动理论的基本方程。对于多孔介质孔隙内部含有两种不同流体，即湿相流体和干相流体的一维问题，方程可以表述为如下形式：

图1 单层非饱和多孔介质示意图Fig.1 Sketch of single layer unsaturated porous media

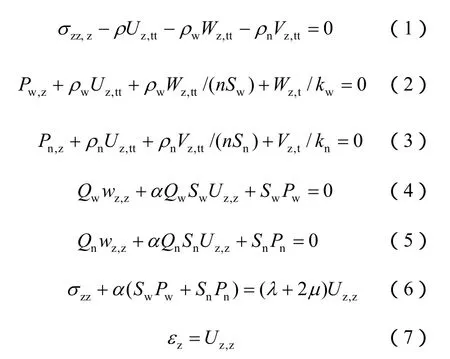
式中：带有下标w或n的变量分别是与湿相或干相流体有关的变量。σz为总应力，以拉为正；Pw和Pn为湿相和干相流体的孔隙流体压力，以压为正，且有称为有效孔隙流体压力；Uz是固体骨架的绝对位移；Wz、Vz分别是湿相和干相的流体相对位移，且有和Vz=为流体的绝对位移；n为孔隙率；Sw和Sn分别为湿相流体和干相流体的饱和度，且有 Sw+Sn=1；ρs、ρw、ρn分别为固体颗粒、湿相流体和干相流体的密度，非饱和多孔介质总体密度为分别为湿相流体和干相流体的动力渗透系数；γ和μ为固体骨架的 Lame常数；α、Qw和Qn均为与固体颗粒和流体压缩性有关的系数，且有(α - n)/Ks+ n/Kn。其中Kb、Ks、Kw和Kn分别为固体骨架、固体颗粒、湿相流体和干相流体的体积模量，且有 Kb=λ+2μ / 3；t为时间。

式（1）、（2）、（3）分别为非饱和多孔介质整体平衡方程和两种流体的运动平衡方程；式（4）、（5）分别为两种流体的渗流连续方程；式（6）为固体骨架的本构方程；式（7）为固体骨架的几何方程。

为方便起见，引入如下无量纲量：

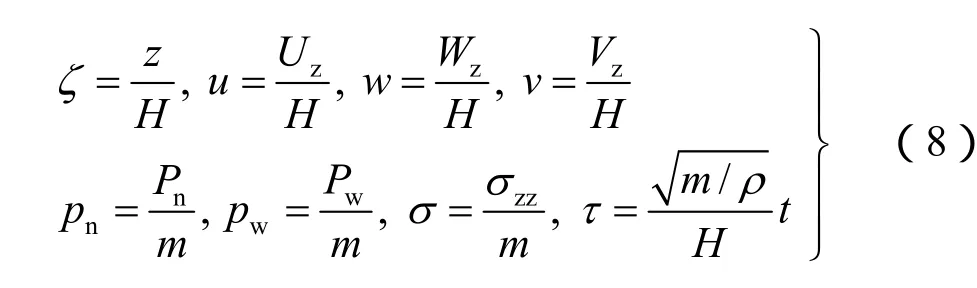
利用上述无量纲量，基本方程（1）～（7）可以写成如下矩阵形式：

其中：

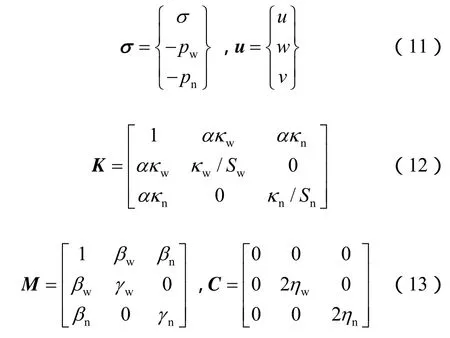
其中：

将式（10）代入式（9）中，得到用位移矢量u表示的控制方程为

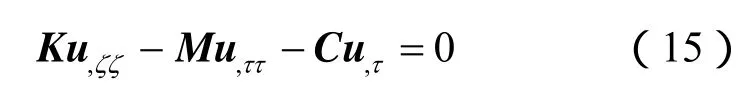
2.2 定解条件

限于篇幅，本文仅以如下混合边界条件为例给出非饱和多孔介质一维瞬态响应半解析解。

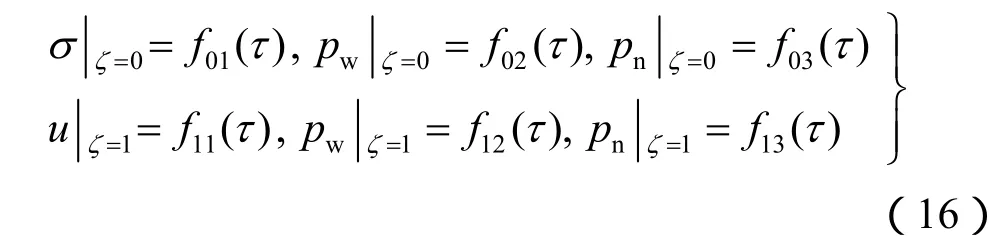
式中： fij(τ)(i = 0,1; j = 1, 2,3)为可以具有任意形式的指定函数。

初始条件为

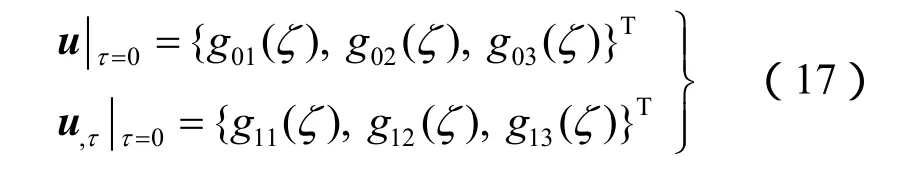
式中： gij(ζ)(i = 0,1; j = 1,2,3)为可以具有任意形式的指定函数。

3 问题的求解

3.1 边界条件齐次化

将位移表达式分解为两部分：

其中：

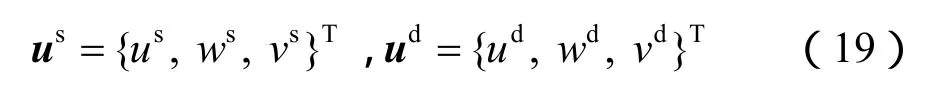
选取适当的 us，使其满足非齐次边界条件（16）。本文选取的 us表达式为

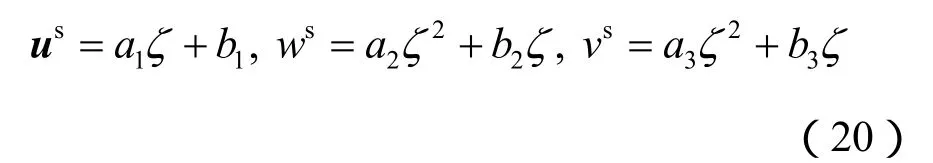
其中：

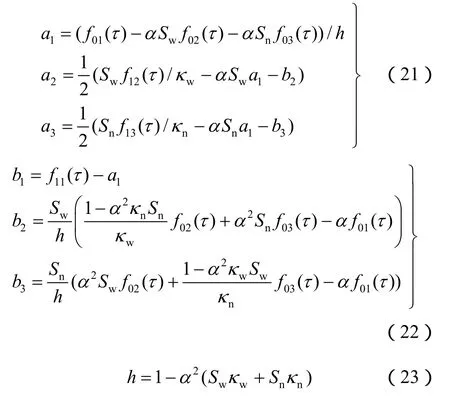
将式（18）代入到式（15），得到 ud表示的控制方程、边界条件和初始条件：

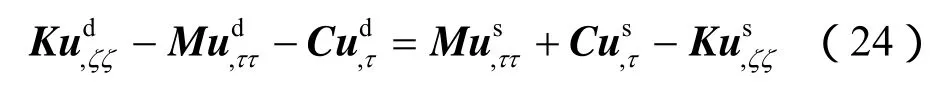
当ζ=0时，有

当ζ=1时，有

当τ=0时，有

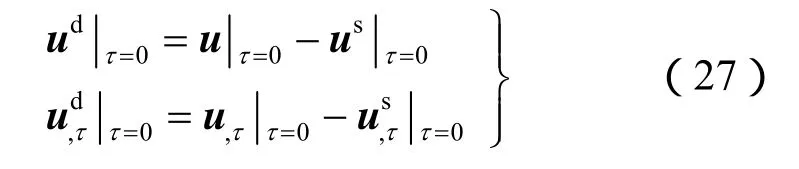
3.2 特征值和特征函数

为了求解 ud，先求 ud对应的无阻尼特征值问题，令

式中：ω≥ 0。式（24）～（26）对应的无阻尼系统特征方程为

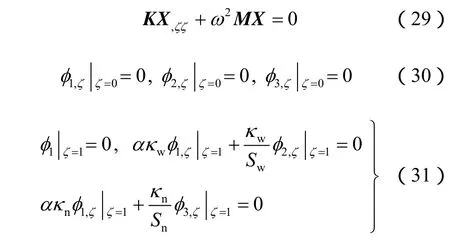
当ω=0时，式（29）具有如下形式的解：

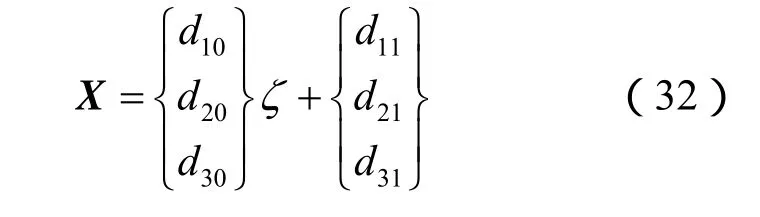
将式（32）代入到式（30）、（31），可求得

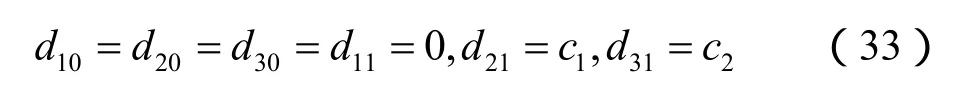
式中：c1、c2为任意常数。可见ω=0对应的两个模态分别为

当ω＞0时，式（29）具有如下形式的解：

式中：βd为待定常数，将式（35）代入式（29）得

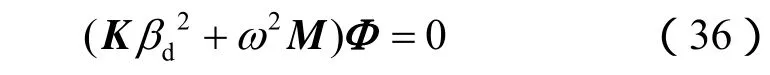
为使方程（36）有非零解，其系数矩阵行列式必须为0。由此可得到如下特征方程：

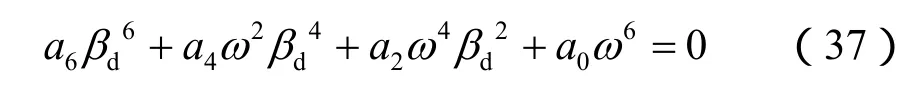
其中：

由式（37）可求得6个特征值，记为βdi(i=1, 2,3, 4, 5, 6)，在一般情况下，βdi均为虚数，且有

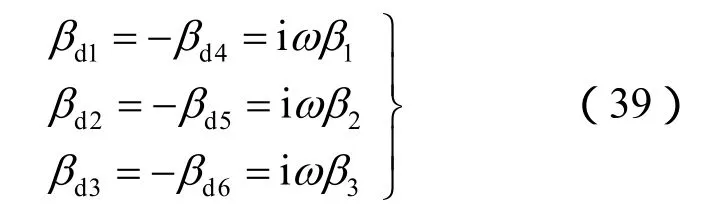
式中：β1、β2、β3是只与材料参数有关，与ω值无关的常数。利用式（35），可求得特征值βdi对应的特征向量，记为Φi(i=1, 2, 3, 4, 5, 6)，则有

其中：

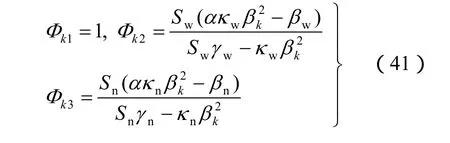
此时X的表达式可以写成：

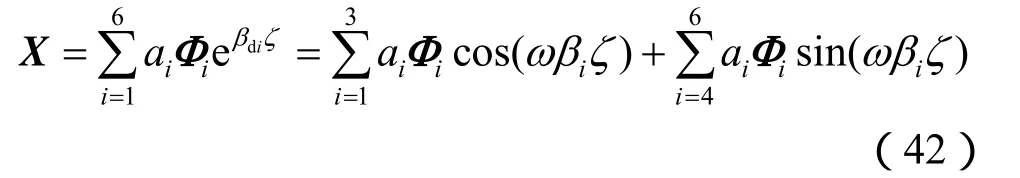
将式（42）代入边界条件（30）得

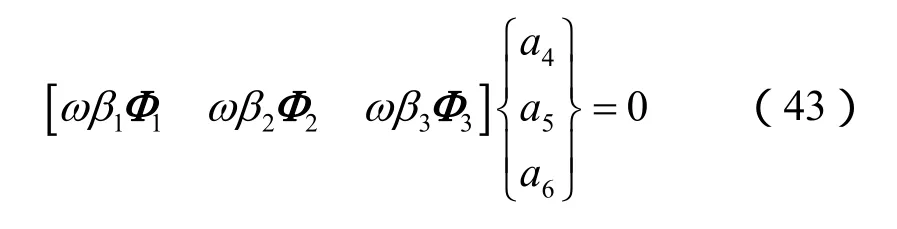
因为方程（43）的系数矩阵行列式不为 0，所以式（43）只有零解，即 a4=a5=a6= 0。此时，式（42）化简为

将式（44）代入边界条件（31）得

式中： i= 1, 2, 3。

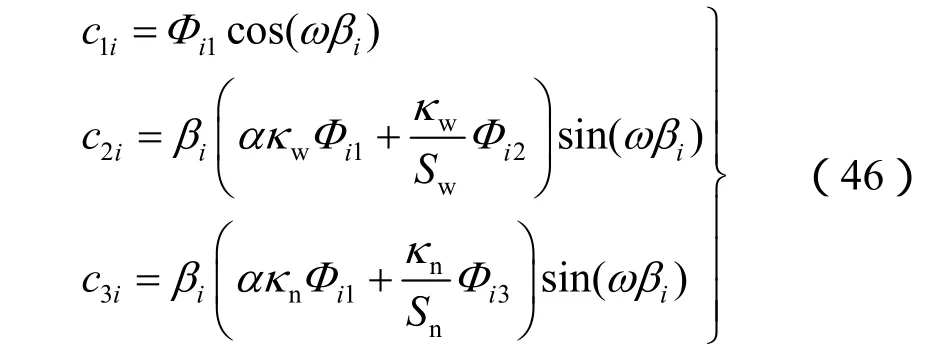
若式（45）有非零解，其系数矩阵行列式必为零，即

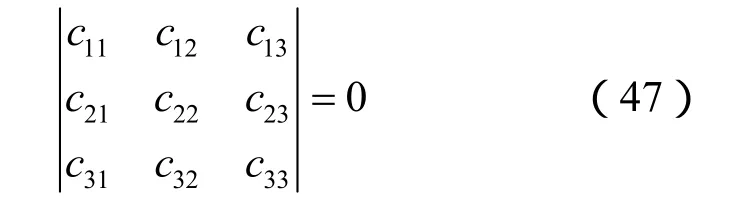
上式即为确定ω的特征方程，由此可得到一系列的特征值，从小到大排列，记第 p(p ≥ 3)个特征值为ωp，记ωp对应的特征向量为由式（45）可求得

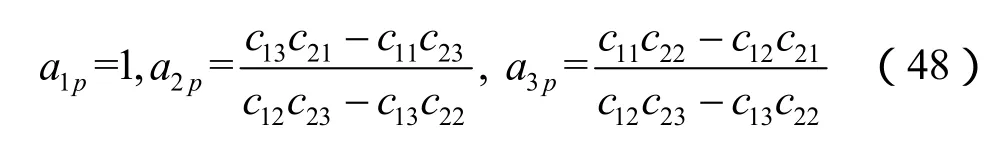
因此，Xp的表达式就可以写成：

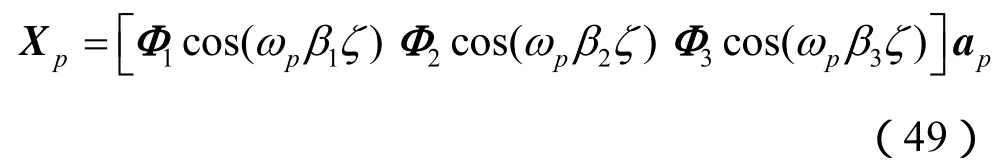
此时所有ω对应的模态都已经求出。为方便起见，记 ω1=ω2= 0，令

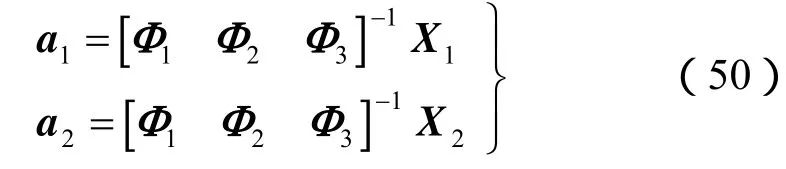
则所有模态均可用式（49）表示，只是p=1,2,3…。

3.3 特征函数的正交性

设ωp和ωq为两个不同的特征值，它们对应的特征函数为Xp和Xq。利用M矩阵的对称性质和式（29）可得

采用分部积分技术并应用边界条件，容易证明上式第一个积分值为0。

将Xp和Xq代入可得

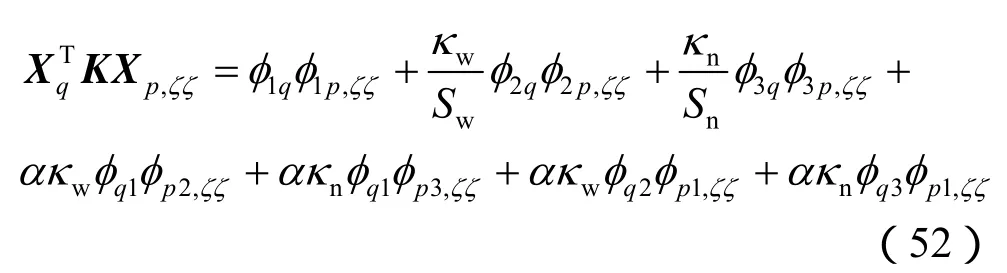
采用分部积分技术，有

根据边界条件（30）、（31），上式可简化为

用同样的方法可以得到

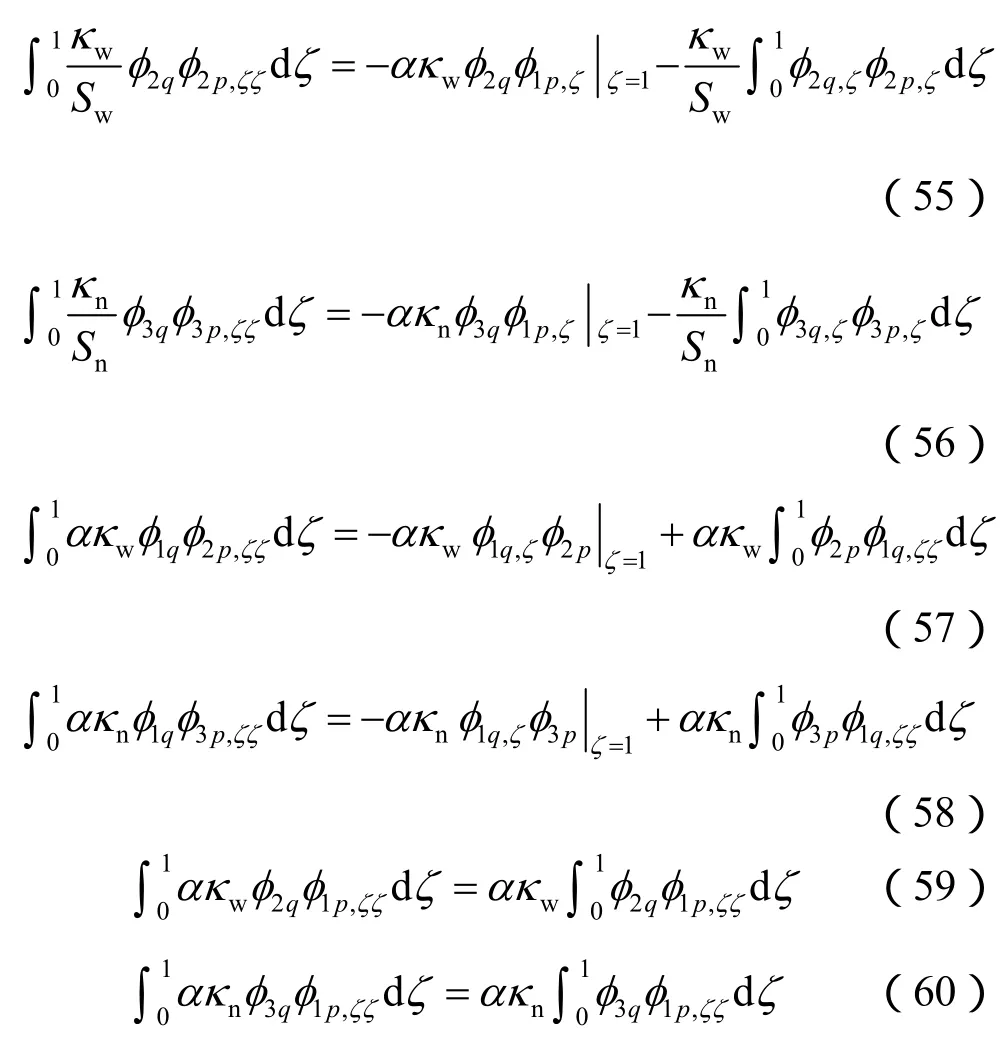
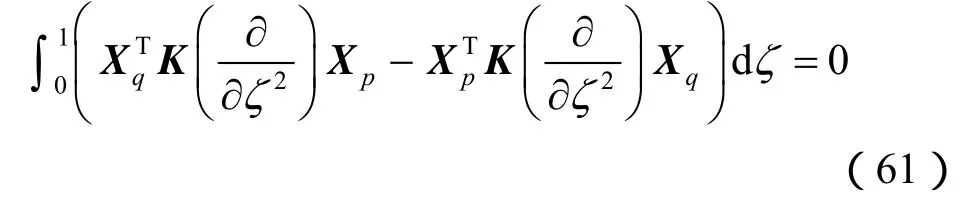
于是，特征函数的正交性就得到证明。

当 ωp≠ωq时，有

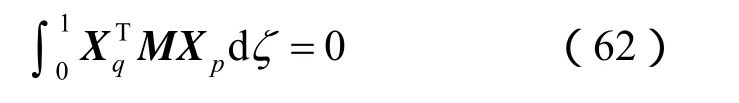
特征函数M的正交性得到证明，为方便起见，将特征函数关于矩阵M规范化处理，定义规范化的特征矢量为

3.4 动力问题的解

对有阻尼系统的受迫振动，根据变异系数法，设 ud具有以下形式的解：

代入式（24），并利用式（29）得

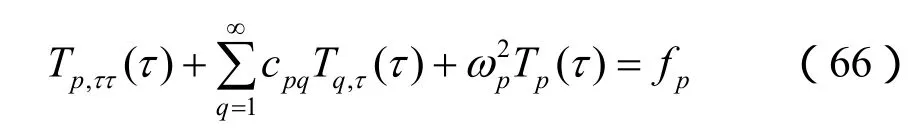
其中：

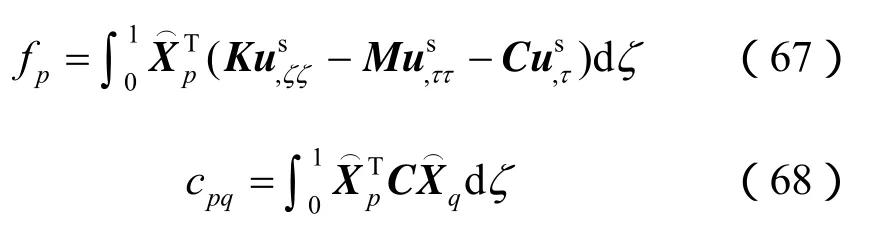
将式（64）代入初始条件（27），得

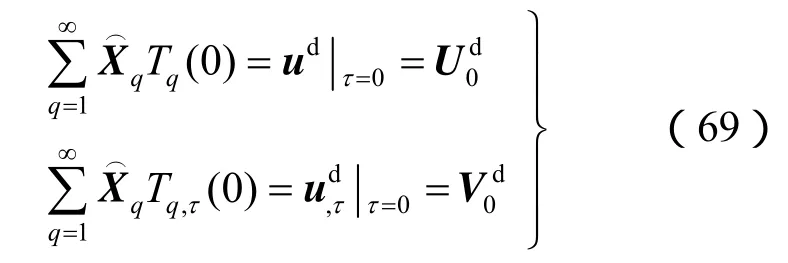
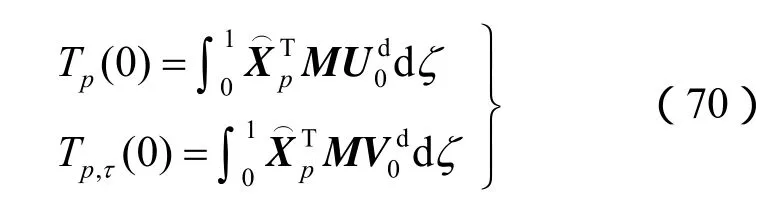
求解由式（66）、（70）构成的初值问题，即可得到 ud，利用式（18）即可得到原问题u的解。

4 常微分方程组的精细时程积分解

常微分方程组（66）中含有无限个常系数微分方程，由于ω已经按照从小到大的顺序排列，因此，在实际求解时，可以根据荷载性质及精度要求截取前N项进行计算。将式（66）改写成如下矩阵形式：

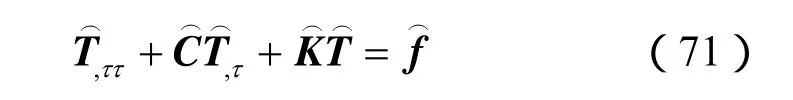
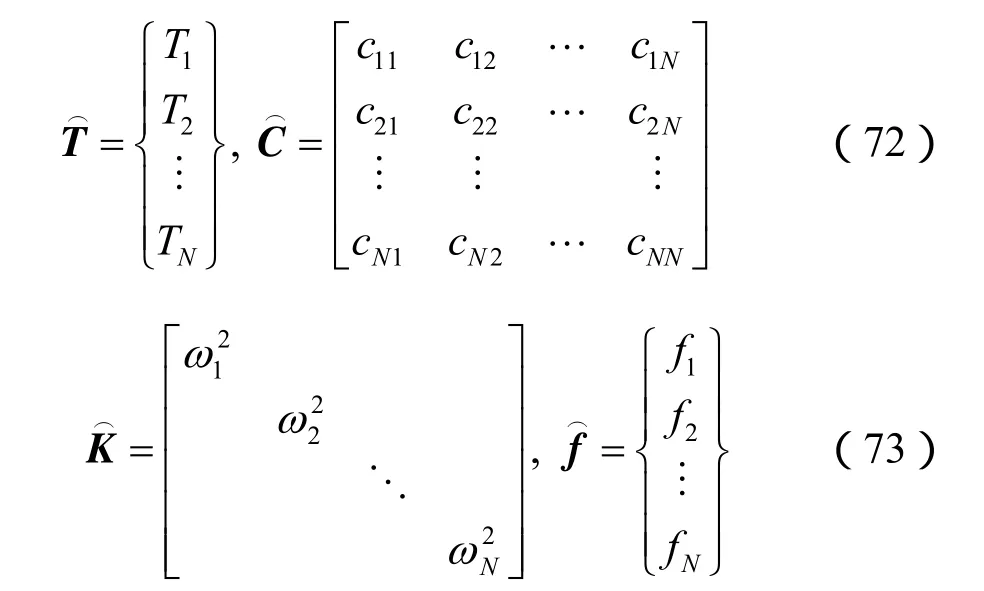
对应的初始条件仍为式（70）。

当湿相流体和干相流体的渗透系数都趋向无穷大时，cpq趋近于0，阻尼阵为零矩阵，式（71）解耦，此时可求得解析解。一般情况下，为满阵，式（70）、（71）构成的初值问题难以获得精确解，本文采用钟万勰[17]提出的精细时程积分法求解上述初值问题。

5 数值算例

以下算例均假定多孔介质内部孔隙充满水和油两种流体，且均满足零初始条件。本文算例选取的材料参数取自文献[18－19]，具体数值如表1所示。

表1 材料参数Table 1 Material parameters

5.1 算例1

截断项数N既关系到计算的精度，又直接影响计算的效率。为考虑N对计算结果的影响，选定上、下表面都完全透水、透气，下表面固定，上表面作用单位阶跃荷载作为边界条件，即

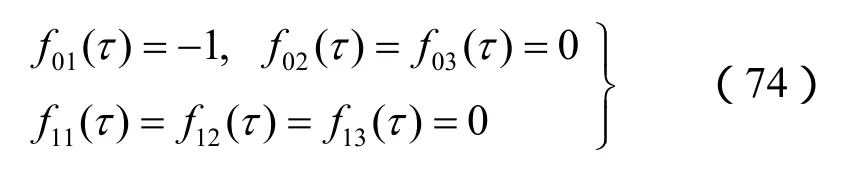
图2给出了边界条件（74）时，两种流体的动力渗透系数kw、kn分别为80、20 m4/(N·s)，N值分别为5、50、500、5 000时，土层中部ζ=0.5处总应力响应时程曲线。

由图 2可以看到，N=5时，曲线不能完整反映土层的动力响应。随着N值的增加，计算响应越来越精确。当 N= 5 000时，可以清晰的观察到三类波的传播，验证了本文方法的合理性与有效性。综合考虑计算效率和计算精度，如没有特别说明，本文算例在阶跃荷载作用时取 N= 5 000，正弦荷载作用时取 N= 1 000。

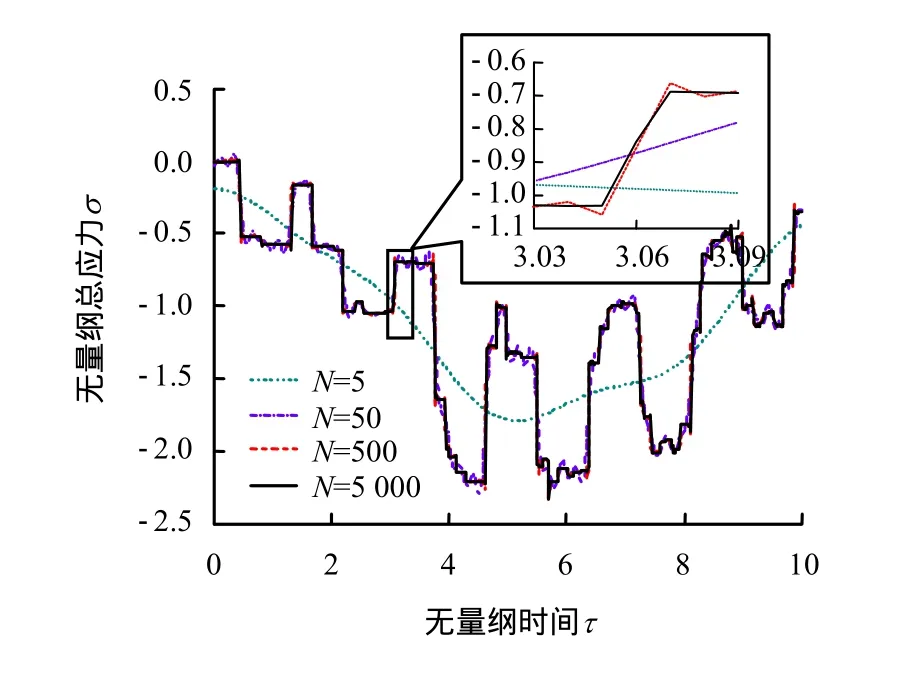
图2 不同截断项数下的响应时程曲线Fig.2 Numerical results for different partial sums of the series solution

为进一步验证本文方法，令非饱和多孔介质内的干相和湿相两种流体都为水，此时，非饱和多孔介质模型就退化为饱和多孔介质。对于非饱和多孔介质模型，边界条件仍采用式（74）。对于饱和多孔介质模型，采用如下边界条件：

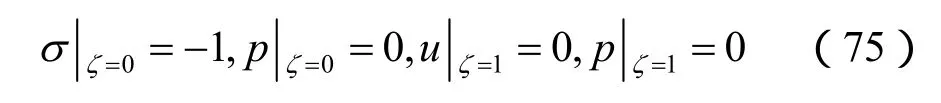
式中：p为饱和多孔介质模型中的孔压。

图3、4给出了动力渗透系数为10-2m4/(N·s)时，分别用本文方法和文献[10]方法计算得到ζ= 0.5处的孔压和流体相对位移响应结果。

由图3、4可以看到，用两种方法计算得到的孔压结果几乎完全一致，而饱和模型中的流体相对位移等于非饱和模型中湿相流体和干相流体的相对位移之和，从而进一步验证了本文提出的非饱和多孔介质动力响应分析方法的有效性。

图3 不同模型的孔隙流体压力-时程曲线对比Fig.3 Pore pressure responses contrast of different models

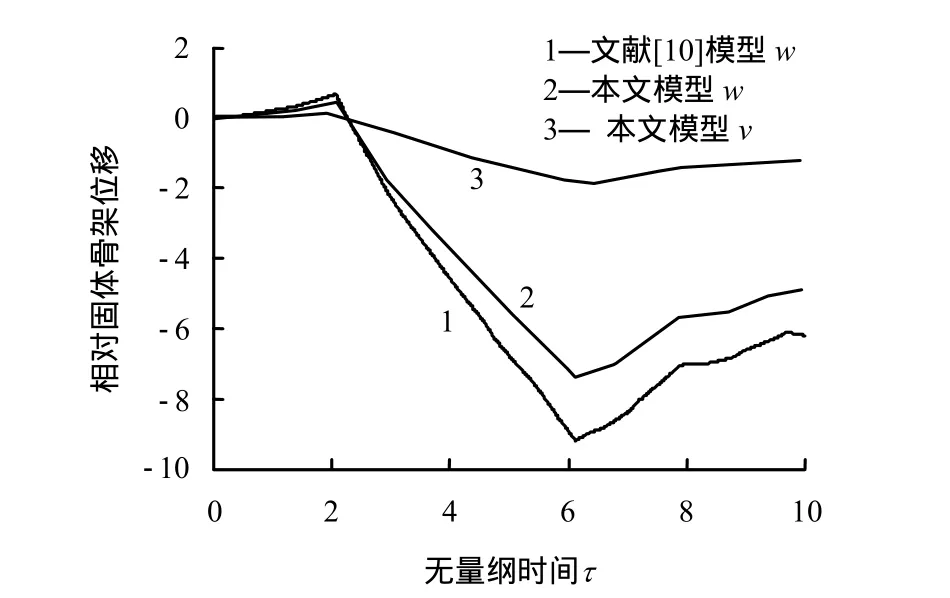
图4 不同模型的流体相对位移-时程曲线对比Fig.4 Fluid relative displacement responses contrast of different models

5.2 算例2

本算例同样选取式（74）作为边界条件，图 5为不同动力渗透系数下土层ζ=0.5处湿相流体孔压pw的响应时程曲线。

由图5可以看到，波在非饱和多孔介质中的传播与衰减特点与饱和多孔介质中相似，但在非饱和多孔介质中明显存在 3类压缩波。如图 5(a)、5(b)所示，当动力渗透系数较大时，这3类压缩波均清晰可见。大量计算表明，当流体渗透系数的数量级大于10-2时，多孔介质的动力响应几乎完全一致；从 10-5量级开始，随着渗透系数减小，流-固间的耦合作用逐渐增大，波的耗散逐渐加快，并在 10-8量级附近达到最大，此时3类压缩波都迅速衰减，看不到明显的波动现象。图5(d)表明，当渗透系数很小时，固体和两种流体之间存在很强的黏滞耦合作用，此时多相孔隙介质呈现单相介质的波动特性。

5.3 算例3

本算例采用如下边界条件：

即土层上、下表面均完全透水、透气，底部固定，土层顶部受到一个完整周期的正弦脉冲荷载作用。

图6为不同动力渗透系数下土层ζ=0.2处的总应力-时程曲线。从图中可以更清晰、直观地反映出不同渗透系数下非饱和土中压缩波的传播和衰减情况。在渗透系数较大时，流-固耦合作用很小，3类压缩波的独立传播非常明显，当渗透系数减小到10-8量级时，受流-固间的黏滞耦合作用，此时只能观察到传播速度较快的第1类波的波形，且波形不完整，说明此时波的耗散非常快。当渗透系数进一步减小到10-11量级时，只能观测到1类波的波形，且波形是完整的，说明此时的多孔介质性质接近于单相介质。

图5 阶跃荷载下ζ =0.5处湿相流体孔压响应曲线Fig.5 Pore pressure responses to step loading at ζ =0.5

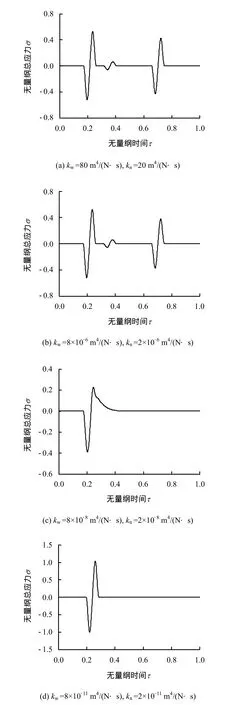
图6 正弦脉冲荷载作用ζ =0.2处总应力响应曲线Fig.6 Stress responses to sinusoidal impulse loading at ζ =0.2

5.4 算例4

本算例分析两种流体的饱和度变化对非饱和多孔介质动力响应的影响，采用如下边界条件：

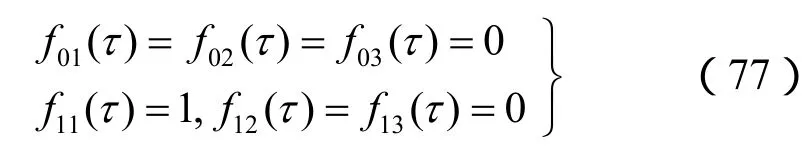
动力渗透系数取kw=80 m4/(N·s)，kn=20 m4/(N·s)，这里无量纲过程中的m=λ+2μ+

图7给出了 4种不同饱和度条件下，介质层ζ= 0.8处的固体位移和两种流体位移-时程曲线。

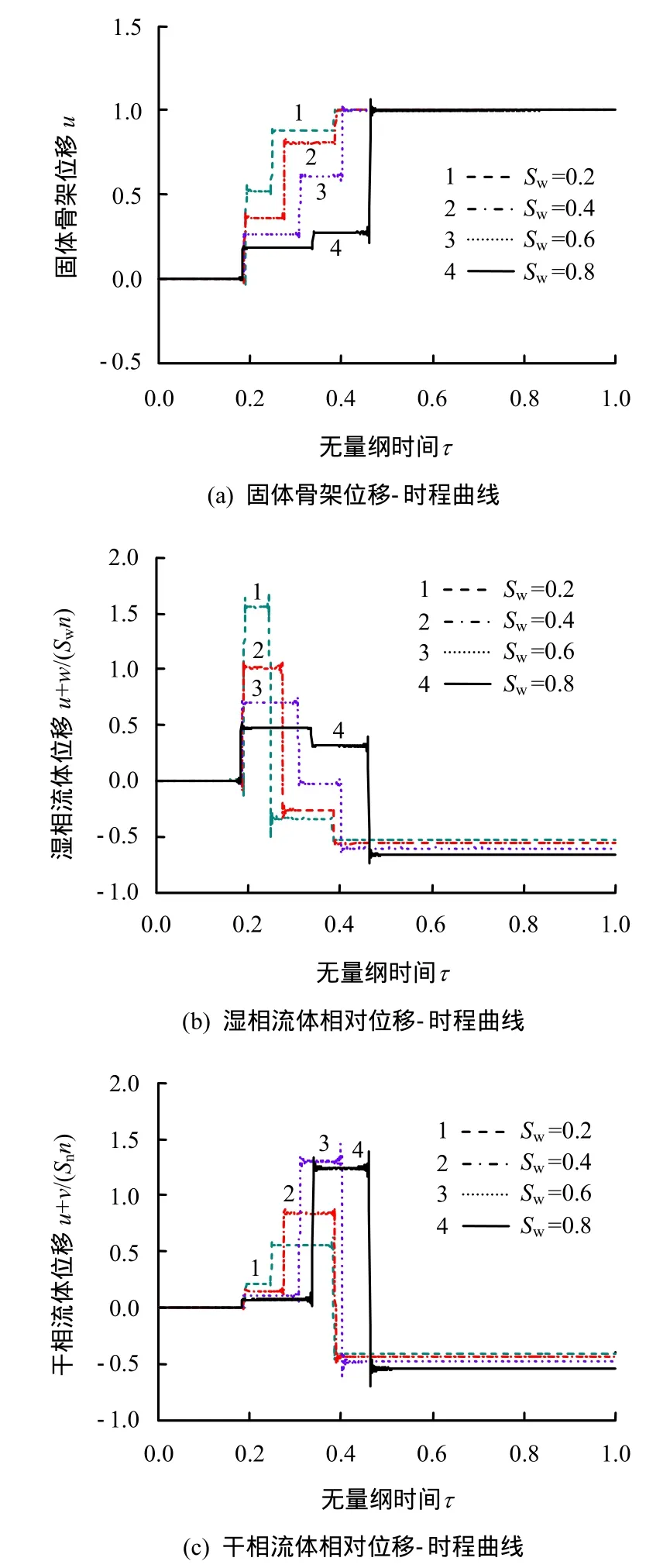
图7 不同饱和度下ζ =0.8处位移响应曲线Fig.7 Displacement responses for different saturations at ζ =0.8

由图7可知，非饱和多孔介质内部两种流体的不同比例会对介质的瞬态响应产生显著影响。图7(a)中可以清楚地观察到 3类压缩波先后传到ζ=0.8处。饱和度的改变对传播速度最快的第1类波速度影响很小，而对第2、2类波的波速影响较大。波速随着湿相流体饱和度的增加而减小。此外，饱和度的改变对3类压缩波的振动幅值和振动相位也有明显影响。

6 结 语

本文基于 Zienkiewicz建立的非饱和多孔介质波动方程，以一类典型的混合边界条件为例提出了一种适用于任意边界条件、任意材料参数的半解析方法。通过算例，验证了本文所建立模型的正确性，探讨了非饱和多孔介质中波传播的特性。

（1）非饱和多孔介质内存在三类压缩波，波速最快的第一类波衰减较小，波速较慢的第二、三类波衰减较明显。

（2）当两种流体的动力渗透系数大于10-2m4/(N·s)量级时，介质层的瞬态响应基本上没有差别；压缩波的衰减随着动力渗透系数的减小逐渐变快，并在10-8m4/(N·s)量级附近达到最大；当渗透系数小于10-10m4/(N·s)量级时，非饱和多孔介质基本上呈现单相介质的波动特性。

（3）三类压缩波波速均随着湿相流体饱和度的增加而减小。同时，当湿相流体饱和度的增加时，第一类压缩波造成固体和流体的位移幅值均有所减少。第二类压缩波造成的固体位移和湿相流体位移减少，而干相流体的位移增加。与之相反的，波速最慢的第三类压缩波造成的固体位移和湿相流体位移增加，而干相流体的位移则有所减少。

[1]COUSSY O. Poromechanics[M]. West Sussex: John Wiley & Sons, 2004.

[2]BIOT M A. Theory of elastic waves in a fluid-saturated porous solid, I: Low-frequency range[J]. The Journal of the Acoustical Society of America, 1956a, 28(2): 168－178.

[3]BIOT M A. Theory of elastic waves in a fluid-saturated porous solid, II: High-frequency range[J]. The Journal of the Acoustical Society of America, 1956b, 28(2): 179－191.

[4]GARG S K, NAYFEH A H, GOOD A J. Compressional waves in fluid-saturated elastic porous media[J]. Journal of Applied Physics, 1974, 45(5): 1968－1974.

[5]SIMON B R, ZIENKIEWICZ O C, PAUL D K. An analytical solution for the transient response of saturated porous elastic solids[J]. International Journal for Numerical and Analytical Methods in Geomechanics,1984, 8(4): 381－398.

[6]GAJO A, MONGIOVI L. Analytical solution for the transient response of saturated linear elastic porous media[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1995, 19(6): 399－413.

[7]SCHANZ M, CHENG A H D. Transient wave propagation in a one-dimensional poroelastic column[J].Acta Mechanica, 2000, 145(1): 1－8.

[8]凌道盛, 张飞霞, 单振东, 等. 单层不可压缩饱和多孔介质一维瞬态响应精确解[J]. 岩土力学, 2011, 32(5):1033－1038.LING Dao-sheng, ZHANG Fei-xia, SHAN Zheng-dong,et al. Exact solution for one-dimensional transient response of single-layer incompressible fluid-saturated porous media under arbitrary vertical loadings[J]. Rock and Soil Mechanics, 2011, 32(5): 1033－1038.

[9]SHAN Z D, LING D S, DING H J. Exact solutions for one-dimensional transient response of fluid-saturated porous media[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35(4):461－479.

[10]凌道盛, 房志辉, 单振东, 等. 单层饱和多孔介质一维瞬态响应半解析解[J]. 岩石力学与工程学报, 2011,30(8): 1683－1689.LING Dao-sheng, FANG Zhi-hui, SHAN Zhen-dong,et al. A semi-analytical solution for one-dimensional transient response of single layered saturated porous media[J]. Chinese Journal of Rock Mechanics and Engineering, 1994, 34(2): 131－136.

[11]LI P, SCHANZ M. Wave propagation in a 1-D partially saturated poroelastic column[J]. Geophysical Journal International, 2011, 184(3): 1341－1353.

[12]SHAN Z D, LING D S, DING H J. Exact solutions for one-dimensional transient response of unsaturated single-layer porous media[J]. Computers and Geotechnics, 2013, 48: 127－133.

[13]BRUTSAERT W. The propagation of elastic waves in unconsolidated unsaturated granular mediums[J]. Journal of Geophysical Research, 1964, 69(2): 243－257.

[14]SCHANZ M, DIEBELS S. A comparative study of Biot′s theory and the linear theory of porous media for wave propagation problems[J]. Acta Mechanica, 2003, 161(3):213－235.

[15]ZIENKIEWICZ O C, CHAN A H C, PASTOR M, et al.Computational geomechanics with special reference to earthquake engineering[M]. Chichester: John Wiley &Sons, 1998.

[16]LI X, ZIENKIEWICZ O C, XIE Y M. A numerical model for immiscible two-phase fluid flow in a porous media and its time domain solution[J]. International Journal for Numerical Methods in Engineering, 1990, 30(6):1195－1212.

[17]钟万勰. 结构动力方程的精细时程积分法[J]. 大连理工大学学报, 1994, 34(2): 131－136.ZHONG Wan-xie. On precise time-integration method for structural dynamics[J]. Journal of Dalian University of Technology, 1994, 34(2): 131－136.

[18]LO W C, SPOSITO G, MAJER E. Wave propagation through elastic porous media containing two immiscible fluids[J]. Water Resources Research, 2005, 41:W02025.

[19]ARNTSEN B, CARCIONE J M. Numerical simulation of the Biot slow wave in water-saturated Nivelsteiner sandstone[J]. Geophysics, 2001, 66(3): 890－896.