无线传感器网络在协同攻击环境中的安全定位研究*

罗 臻， 刘宏立， 徐 琨

(湖南大学 电气与信息工程学院，湖南 长沙 410082)

0 引 言

随着信息技术的快速发展，无线传感器网络越来越多地被用于军事和民用领域,一个典型的应用是监测感兴趣区域中的对象或估计对象的位置。近几年来，研究者们提出了很多种关于无线传感器网络的定位算法[1～6]，这些算法大多都没有考虑恶意节点或攻击者的影响。当无线传感器网络部署在恶意危险的环境中时，很可能存在攻击者不断地尝试对网络发起各式各样的攻击，从而影响节点的正常定位，因此，安全定位是非常重要的。

最近已经有研究人员提出了几种用于无线传感器网络的安全定位算法[7～11]。文献[8]中提出了一种最小中位数二乘(least median of squares，LMS)估计法，通过最小化误差平方的中位数来估算位置，具有较强的抗攻击能力。文献[10]中提出了一种基于投票的定位算法，通过将网络区域量化成一个网格并采取投票选举的方式来容忍攻击。

对于基于距离的定位算法，无线传感器网络面临的攻击大致可以分为两类：1)单个或多个恶意锚节点独立地对网络进行攻击，发送互不相关的数据给定位节点，恶意锚节点之间没有相互协作，称之为非协同攻击；2)多个恶意锚节点串通起来对网络进行攻击，不仅影响定位准确度，而且可以诱导节点定位到攻击者任意指定的位置，称之为协同攻击。本文主要考虑协同攻击对网络产生的影响，提出了一种能够抵御协同攻击的安全定位算法，该算法通过矢量关系分辨出正常锚节点和恶意锚节点，并把恶意锚节点从网络中剔除，从而消除掉恶意锚节点对定位结果造成的影响，同时采用分布式计算，由定位节点自行计算自己的位置，减少了节点的能耗，从而增加了整个网络的生存时间。

1 无线传感器网络安全定位分析与建模

无线传感器网络的定位算法包括两大类：一类是无需测量节点间距离，称之为Range-free的定位算法；另一类是需要测量节点间距离，然后使用三边测量法或三角测量法来计算节点位置，称之为Range-based的定位算法。

在Range-based的定位算法中，定位节点需要收到一些{(x，y，d)}信息集，其中，d表示定位节点到位于(x，y)的锚节点的距离估计值。这个距离d可以由不同的测量方法获得，如到达时间(TOA)、到达时间差(TDOA)、到达角度(AOA)和接收信号强度指示(RSSI)等。例如：在基于RSSI的定位算法中，锚节点向网络中发送一系列信标信号，定位节点接收到这些信标信号并测量其信号强度，然后可以将RSSI转换为距离估计值。

在理想的情况下，也就是测量数据不受到任何噪声干扰时，这些{(x，y，d)}信息集形成一个圆，即有

d2(x,y)=(x-x0)2+(y-y0)2.

(1)

其中,(x0,y0)是定位节点的位置。在实际应用中，距离的测量往往带有测量噪声，那么，收到一些{(x,y,d)}信息集然后求解(x0,y0)就是一个由超定方程组和测量噪声引起的最小二乘(LS)问题。

然而，这样的方法应用在对{(x，y，d)}信息集有恶意攻击的情况下并不合适。例如:如果攻击者俘获了一些锚节点使其成为了恶意锚节点，然后这些恶意锚节点互相协作向网络中发送错误的信标信号，就可能导致测量距离d与其真实值之间出现重大偏差。即使在大部分{(x，y，d)}信息集都是正确的情况下，只要存在一些明显不正确的{(x，y，d)}信息集就将使定位节点的位置估计值远远偏离真实值。

2 协同攻击及其数学模型

Range-based的定位算法都是建立在测量节点之间距离的基础上。表1中列举了几种用来测量距离的物理特性和攻击者针对各特性可采取的攻击方式。这些攻击是Range-based的定位算法所特有的，主要是为了阻碍节点之间准确的距离测量，因此，这些攻击可以绕过常规的安全检测。例如:在使用TOA或者TDOA测距技术的定位系统中，攻击者俘获锚节点之后可以故意延迟或提前发送响应报文,从而达到增加或减少定位节点和锚节点之间距离的目的。

表1 距离测量特性及其针对这些特性的攻击

实际中，单一恶意锚节点的攻击对无线传感器网络的影响作用不是很明显。攻击者往往希望俘获网络中的多个锚节点，拥有网络中尽可能多的资源，然后联合起来对网络发起协同攻击。这样，不但可以阻碍其他节点的准确定位，甚至可以随意改变定位结果，使节点定位到攻击者任意指定的位置上，协同攻击比非协同攻击对网络的威胁更大。

不失一般性，假设在攻击过程中恶意锚节点只改变距离d值，这样的假设是合理的，因为改变其他任何参数都可以同等地转换为改变d值。协同攻击是由多个恶意锚节点一起协作，使定位节点定位到攻击者任意指定的位置Pmal=[xmal,ymal]T。在这种情况下，假设定位节点计算出的距离d为恶意锚节点的位置Pk与攻击者期望定位到的位置Pmal之间的距离，定义

其中，distk为第k个锚节点与定位节点的真实距离，nk为均值为0，方差为σ2的加性高斯噪声。定位节点接收到各锚节点发来的{(Pk,dk)},k=1,2,…,N信息集，然后用这些信息来确定自己的位置。协同攻击的攻击强度由da=|P-Pmal|决定，其表示定位节点的真实位置和攻击者指定的位置之间的距离。

3 安全定位算法

本节提出了一种计算高效的基于梯度下降法的迭代安全定位算法。注意到，当测量噪声为高斯噪声，环境区域中不存在恶意锚节点时，任意给定的点(X,Y)是节点真实位置的概率正比于负的误差平方和，即

那么,节点位置的最大似然估计就是使概率达到最大值的点，或者说是使概率的相反数达到最小值的点。本算法采用梯度下降法一步步迭代缩小误差平方和，然后确定节点位置的最大似然估计。

从直观上讲，该算法可以看作是围绕锚节点(xk,yk)以半径dk画圆。因为节点的真实位置应位于靠近这些圆的某点上，所以,在每次迭代中算法将估计的位置往靠近这些圆的地方移动。为了便于描述，定义一个称为“势矢量”的向量，其方向为当前估计值指向锚节点(xk,yk)，其大小等于当前估计值与锚节点(xk,yk)所对应圆的距离。根据定义可知，“势矢量”与当前估计值和锚节点的位置有关，每个锚节点都会对应有一个“势矢量”，因为在每一步迭代中，位置估计值都会有所变化，所以,每一步迭代的“势矢量”也会有变化。在一步迭代的过程中，所有“势矢量”之和就构成了这一步迭代的梯度。

算法开始时，首先初始化一个随机点，在第i步迭代中，前一步估计值向梯度方向移动一个步长δ(i)来获得新的估计值。这样的迭代方法使得新的估计值具有更高的概率是节点的真实位置，并最终收敛到LS估计。如前所述，在存在攻击者的情况下，LS估计可能会有很大的误差。因此，一旦梯度下降法收敛后就转换到攻击检测阶段，这一阶段会对“势矢量”进行一些挑选和过滤。

攻击检测阶段：实验表明，梯度下降法收敛以后得到的LS估计相对于由攻击者所选择的位置(xmal,ymal)会更接近节点的真实位置(xtrue,ytrue)。因此，那些正常锚节点对应的“势矢量”的模值将会比恶意锚节点对应的“势矢量”的模值要小。利用这一点可以过滤掉恶意锚节点提供的信息。首先将“势矢量”按模值从小到大排序，选择参数差分阈值β，若相邻两“势矢量”模值相差达到β，则丢弃其后面模值较大的“势矢量”，使用前面模值较小的“势矢量”来确定后续迭代的梯度。

4 算法仿真与性能分析

本节通过仿真对本算法的一些参数和性能进行了分析，并在相同条件下与文献中的其他算法进行了比较。假设20个锚节点随机部署在一个大小为100 m×100 m的区域中，测量噪声的标准差为σ=1 m，迭代次数M=200，初始迭代位置选择区域中心点(50，50)m。对于LMDS算法，子集的个数为20，每个子集中的节点数为4。所得的曲线均为500次运行计算的平均值。

图1显示了30 %恶意锚节点协同攻击下的迭代收敛曲线。由图可知，采用可变步长可以使定位误差更小，但是收敛速度较慢；而采用固定步长则定位误差稍大，但收敛速度更快，这是在运用梯度下降法时一个普遍的现象。从图中还可以观察到当采用可变步长时，在迭代大约150次左右定位误差会突然减小。这种现象的原因是算法已经进入了攻击检测阶段，这一阶段中，通过过滤掉恶意锚节点发送的信息，估计值开始远离LS估计并朝着正确的位置移动。

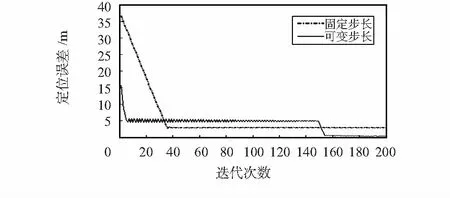
图1 30 %恶意锚节点协同攻击下的收敛曲线(攻击强度da=28 m)

图2为在不同攻击强度的情况下，差分阈值β的大小对定位精度的影响关系曲线，其中x轴表示差分阈值β的大小，y轴表示定位误差。从图中可以看到，当β值较小时，定位误差随着β的增大而减小，当β达到一定值时(图中大概为1.5)，定位误差达到极小值，随后随着β的增大，定位误差也会增大并随着攻击强度的不同而有所变化。当攻击强度较小时(如图中dα=10 m)，定位误差达到极小值之后会马上呈现上升的趋势；当da=16 m时，定位误差会在β的一定区间范围内保持稳定之后才会上升；当攻击强度较大时(如图中da=22 m,da=28 m)，取得最小定位误差的β值会有所变大，并且之后定位误差的上升趋势较为缓慢，一定程度上可以看做是保持稳定。

图2 定位误差与差分阈值β的关系

图3为30 %恶意锚节点协同攻击下定位误差与攻击强度的关系。x轴表示节点的真实位置(xtrue,ytrue)和恶意锚节点协同指定的点(xmal,ymal)之间的距离，即攻击强度da。从图中可以观察到，当恶意锚节点数占30 %时，本文算法在攻击强度较小和攻击强度较大的情况下优于LMS算法，而LS算法则不能抵御协同攻击。本文同样也仿真了当恶意锚节点数为35 %时的情况，此时，本文提出的算法比LMS算法的定位误差高大约1 m左右。这种现象的原因是，当恶意锚节点数增加时，一些距真实位置和恶意位置大致相同的锚节点可能导致数据更符合恶意位置。因此，当恶意锚节点数较高时，梯度下降法的性能略逊于LMS算法。在一般情况下，当恶意锚节点数少于50 %时，本算法是可以很好地抵御协同攻击的。

图3 30 %恶意锚节点协同攻击下的不同定位算法比较

5 结束语

本文介绍了一种计算简单的用于在恶意危险环境下的无线传感器网络安全定位算法。本算法采用梯度下降法并结合攻击检测技术，以确定一个给定区域中的节点位置。仿真结果表明：当恶意锚节点数占30 %时，算法收敛性较好，选择可变步长和合适的差分阈值β可使定位精度更高，相较于LMS算法而言，本算法具有更好的定位效果，平均定位误差不超过2 m。

参考文献:

[1] Li D,Hu Y H.Energy-based collaborative source localization using acoustic microsensor array[J].EURASIP Journal on Advances in Signal Processing,2003,4:321-337.

[2] Sheng X,Hu Y H.Maximum likelihood multiple-source localization using acoustic energy measurement with wireless sensor networks[J].IEEE Transactions on Signal Processing,2005,53(1):44-53.

[3] Ruixin N,Varshney P K.Target location estimation in sensor networks with quantized data[J].IEEE Transactions on Signal Processing,2006,54(12):4519-4528.

[4] 张广峰,段其昌,刘 政.基于加强学习与联想记忆粒子群优化算法的节点定位[J].传感器与微系统,2013,32(3):72-77.

[5] 胡中栋,贾方方.基于角度判断的无线传感器网络APIT定位算法研究[J].传感器与微系统,2013,32(1):73-75.

[6] 裴菊静,王经卓,许红艳.基于CC2510的DV-Hop定位算法的改进[J].传感器与微系统,2013,32(1):135-140.

[7] Boukerche A,Oliveira H A B,Nakamura E F,et al.Secure localization algorithms for wireless sensor networks[J].Communications Magazine,2008,46(4):96-101.

[8] Li Z,Trappe W,Zhang Y,et al.Robust statistical methods for securing wireless localization in sensor networks[C]∥Proc of IPSN 2005,Los Angeles:IEEE Computer Society,2005:91-98.

[9] Yanchao Z,Wei L,Yuguang F.Secure localization in wireless sensor networks[C]∥Military Communications Conference,2005:3169-3175.

[10] Liu D,Ning P,Du W K.Attack-resistant location estimation in sensor networks[C]∥Proc of IPSN 2005,Los Angeles:IEEE Computer Society,2005:99-106.

[11] Rawat A S,Anand P,Chen H,et al.Collaborative spectrum sen-sing in the presence of Byzantine attacks in cognitive radio networks[J].IEEE Transactions on Signal Processing,2011,59(2):774-786.