基于Fisher信息距离的被动传感器目标协同跟踪方法

王 勇

(1.中国矿业大学 信息与电气工程学院，江苏 徐州 221116；2.徐州工业职业技术学院，江苏 徐州 221140)

0 引 言

随着现代战争的需要和传感器技术的迅速发展，多传感器数据融合技术得到了广泛的应用。在现有的多传感器目标跟踪系统中， 传感器的多样性和信息来源的广泛性和复杂性，不仅限制了对传感器信息资源的有效利用，而且严重影响了传感器的合理使用。因此，研究对有限的传感器资源进行科学合理的分配，实现多传感器的协同探测已成为目前亟待解决的问题[1]。

从信息论的角度出发，当传感器对目标定位时或被跟踪目标的状态估计的精确度提高时目标的信息有所增加，即通过传感器对目标的观测使目标的位置估计得到更新，从而减少了目标位置的不确定性。文献[2]在对目标的状态估计过程中，将信息增量的含义推广为在获得新的量测条件下，定量表述目标状态不确定性的改变，并且将信息熵定义为估计误差协方差矩阵形式。文献[3]则根据Rényi差异求得信息增量，并基于此解决了大规模动态网络的传感器资源管理问题。文献[4]通过贝叶斯网络建立量测过程模型，采用分辨力增量实现异类传感器融合中目标分类的最优化。文献[5]针对传感器网络中机动目标跟踪问题，提出了一种基于Rényi信息增量的机动目标协同跟踪方法。文献[6]利用信息增量对被动传感器资源分配算法进行了研究。最近，文献[7]利用信息几何理论，以Fisher信息距离来定义目标之间的区分度，并直接依据目标之间的区分度制定传感器资源分配策略。

本文针对多被动传感器目标跟踪问题，在无迹卡尔曼粒子滤波算法的框架下，利用Fisher信息距离来计算观测到来之前的先验概率密度函数和获得观测后的后验概率密度函数之间的信息增量，选择信息增量最大的传感器进行目标跟踪。仿真实验表明:本文所提算法能够显著提高目标的跟踪精度，实现协同跟踪。

1 Fisher信息距离

1.1 基本理论

考虑如下概率分布族

P=p(x;ζ).

(1)

其中,x为随机向量，ζ=(ζ1,ζ2,…,ζn)为概率分布的参数，它是一个包含n个元素的向量。每一个参数ζ对应一个概率分布p(x;ζ)。从几何的观点来看，概率分布族P可以看做高维空间中的n维流形。在统计流形中，流形上的每一个点代表了一个概率分布函数，因此，概率密度函数之间的差异可以用流形中点之间的距离来度量,通常采用随机变量的Fisher信息作为度量张量,其定义如下[7]

(2)

其中，ζ1和ζ2分别对应概率密度函数p(x;ζ1)和p(x;ζ2)，则概率密度函数p(x;ζ1)和p(x;ζ2)之间的距离即为统计流形中对应点ζ1和ζ2之间的距离；[gij]为Fisher信息矩阵，各元素定义如下

(3)

此处E[·]表示关于p(x)的期望，也就是

(4)

在信息几何理论中，由于每个概率分布函数都被抽象为统计流形上的一个点，潜移默化实现了“去随机性”。因此，信息几何有潜力将统计学中的随机性问题变为一个确定性问题来求解，实现现有方法的革新。

1.2 Fisher信息距离的计算

直接计算Fisher信息距离需要大量的计算资源。本文采用文献[7]给出的基于完全的Isomap(isometric feature mapping)算法的Fisher信息距离近似求解方法。结合本文背景，具体算法步骤如下

2)对距离矩阵DG进行初始化

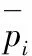
(5)

由于本文是在无迹卡尔曼粒子滤波的框架下进行跟踪，故

(6)

其中，wk为k个粒子的权值，p(z|xk)为似然函数，p(z)为观测的边缘分布函数，其表达式为

(7)

3)对距离矩阵中每个元素依次进行遍历，用D(i,j),D(i,d)+D(d,j)中较小的值来替换D(i,j),d=1,2,…，M，从而得到距离矩阵DG,并得到DF(p1,p2)。

2 基于Fisher信息的被动传感器协同跟踪

2.1 多被动传感器资源协同分配模型

设被动传感器跟踪系统中有Ms只传感器，各被动传感器使用成本相同且已进行时空对准，每只传感器能够探测和跟踪的最大目标数为m。这些传感器构成基本集合为S={1,2,…,Ms}，将集合S的子集全体(除去空集)记为扩展集合D，并记第r个子集为Dr，Dr中所包含的传感器数目为Mr，则集合D的每一个元素Dr描述了一种可能的传感器组合，所有传感器组合的数目为2Ms-1。假设在探测区域内，目标的数目为N，当传感器组合Dr分配给目标n时获得的信息增量为IDin。

建立如下线性规划模型

(8)

约束条件：

1)传感器分配约束

(9)

2)每个目标的最大被跟踪容量约束

(10)

3)每部传感器最大跟踪能力约束

(11)

其中,G为系统总体信息增量和；Ds为传感器组合总数。

式(10)给出了每个目标被跟踪容量约束，式(11)给出了每只传感器最大跟踪能力约束，从而确保被跟踪的目标数量不超过传感器的最大跟踪能力[6]。

2.2 算法实现步骤

多被动传感器协同目标跟踪算法步骤如下：

1)将所有的被动传感器进行分组；

2)每个传感器组合利用UPF获得目标状态的先验概率密度、后验概率密度函数；

3)对于每个传感器组合计算跟踪不同目标时获得的Fisher信息增量；

4)建立线性规划模型对传感器资源进行分配，求出满足约束条件时系统总体的信息增量和最优分配方案；

5)输出最优分配方案进行滤波跟踪。

3 仿真实验分析

3.1 仿真场景设置

本文所提的算法与无迹粒子滤波与协方差矩阵相结合的方法进行了比较分析。设观测区域x为[0,100]m,y为[0,100]m内随机分布10只被动传感器，各传感器的测角误差标准差σ相同，且均为1 mrad，系统采样周期T=1 s，每只传感器最大跟踪目标数为2。3个目标在观测区域内做匀速直线运动，运行时间为30 s，目标运动模型采用CV模型，粒子数为200，蒙特—卡罗次数为50次。当目标进行运动时，Fisher信息距离的求解作为目标跟踪的一部分融入整个跟踪滤波递推过程。图1给出了仿真实验的态势图，其中包括3个目标的运动轨迹和被动传感器系统中10只随机分布的传感器位置。

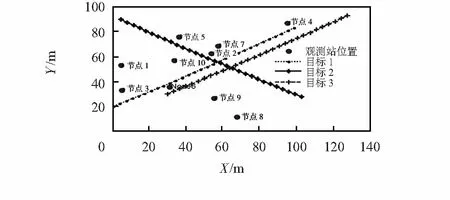
图1 目标与传感器分布态势图

3.2 实验结果与分析

图2和图3给出了1次蒙特—卡罗仿真各目标相应的传感器选择结果。从仿真结果来看，由于各被动传感器测角误差相同，所以，传感器的选择一定程度上取决于目标与传感器的距离。

图4为50次蒙特—卡罗实验的均方根误差曲线图。从结果可以看出：在跟踪区域内，采用本文方法获得的3个目标的位置误差均优于无迹粒子滤波与协方差矩阵相结合的方法。这是因为与本文提出的方法相比，在非线性非高斯环境下，协方差矩阵表征的只是后验概率密度函数的一个特征值，用其来衡量跟踪精度是不准确的，从而做出的跟踪传感器选择方案亦不是最优的。而本文的方法是利用大量粒子来近似先验概率密度函数和、后验概率密度函数，比较的是概率密度函数的近似程度，因此，Fisher信息距离包含了更多的信息，可以较为准确地描述传感器对目标跟踪的贡献，从而可以在合适时间选择恰当的传感器对目标进行精确协同跟踪，避免传感器资源的浪费。因此，本文所给出的算法可以动态地选择跟踪性能较好的传感器进行跟踪，从而实现传感器协同跟踪，显著提高系统的整体跟踪性能。

3.3 算法时间复杂度分析

表1列出了10只传感器3个目标50次蒙特—卡罗仿真实验算法复杂度对比情况，包括算法的平均运行时间和相对计算强度(将协方差矩阵法计算强度设为1，相对计算强度无量纲)。由表1可看出：所提算法运算时间有了明显地增加，额外的计算量主要用于计算先验概率密度函数和后验概率密度函数之间的Fisher信息距离。

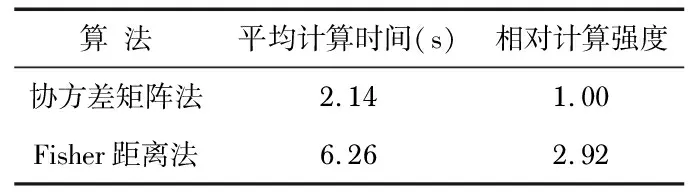
表1 算法计算复杂度

综合上述实验结果，本文所提算法可以自适应地选择跟踪性能较好的传感器进行协同跟踪，显著地提高了跟踪精度，但同时也增加了一定的计算复杂度。

4 结 论

本文针对多被动传感器协同跟踪问题进行了研究，依据信息几何理论，以流形中的Fisher信息距离来衡量先验概率密度函数和后验概率密度函数之间的距离，继而以此距离为依据动态选择传感器进行目标跟踪。与传统的协同跟踪算法相比，能够更加充分地体现出信息熵的变化。仿真实验验证了算法的可行性、优越性和动态环境中的自适应性。

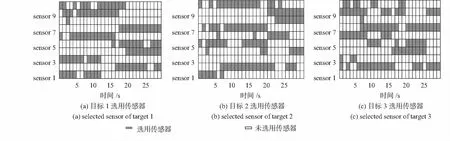
图2 本文算法传感器选择情况

图3 协方差法传感器选择情况

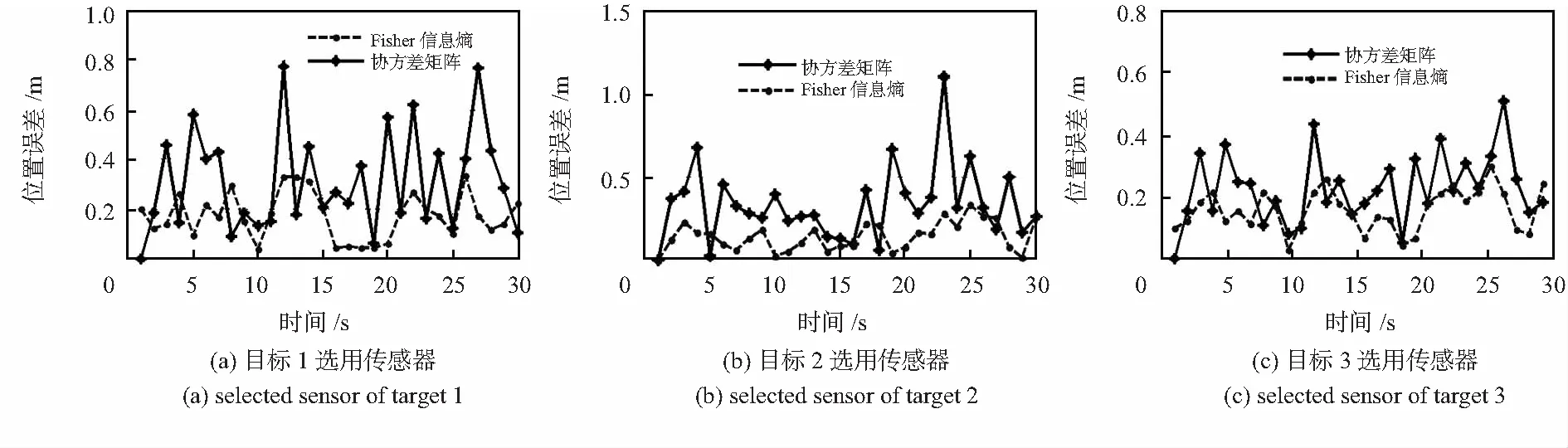
图4 目标跟踪位置误差

参考文献:

[1] 罗开平，姜 维，李一军.传感器管理评述[J].电子学报，2010，38(8):1901-1907.

[2] Hintz K J,Mcvey E S.Multi-process constrained estimation[J].IEEE Trans on Systems,Man and Cybernetics,1991,21(1):434-442.

[3] Kreucher C M,Hero A O,Kastella K D,et al.An information-based approach to sensor management in large dynamic network-s[C]∥Proc of the IEEE,2007,95(5):976-999.

[4] Yang Chun,Kadar Ivan,Blasch Erik.Comparison of information Theoretic divergences for sensor management[C]∥Proc of the SPIE Signal Processing,Sensor Fusion and Target Recognition,2011,8050:1-9.

[5] 刘 钦，刘 铮．一种基于Rényi信息增量的机动目标协同跟踪方法[J].控制与决策，2012，27(9):1437-1440．

[6] 李彬彬，冯新喜，王朝英，等.基于信息增量的多被动传感器资源分配算法[J].系统工程与电子技术，2012,34(3):502-507.

[7] 张华睿，杨宏文，胡卫东，等.基于Fisher信息距离的传感器管理方法[J].系统工程与电子技术，2012，34(8):1587-1591.

[8] Lapuyade-Lahorgur J,Barbaresco F.Radar detection using siegel diatance between autoregressive processed,application to HF and X-band radar[C]∥Proc of IEEE Radar Conference,2008:1-6.