基于视频传感器网络的高效分布式跟踪方法*
2014-09-20王典洪
方 武, 王典洪, 王 勇
(1.中国地质大学(武汉) 机电学院,湖北 武汉 430074;2.苏州经贸学院 信息系,江苏 苏州 215009)
0 引 言
在无线视频传感器网络的许多应用中[1],首先需要对图像序列的目标进行检测和跟踪。为提高跟踪精度和范围,视频节点需要相互通信来对目标进行分布式跟踪。所谓分布式跟踪是指依赖节点间多视角的目标信息的交换与融合,通过本地运算获得目标位置轨迹信息的方式。然而,受传感器节点资源和能耗的限制,传统的目标跟踪方法并不适合视频传感器网络。适用于视频传感器网络的高效分布式跟踪算法需要尽量减少节点之间的通信量以减少能量消耗,从而延长网络寿命。
近几年,一些文献对分布式跟踪算法[2,3]在无线传感器网络当中的应用进行了研究。最常用的分布式跟踪算法包括粒子滤波[4]和卡尔曼一致性滤波(Kalman consensus filtering,KCF)。然而,粒子滤波采用蒙特—卡罗方法,计算量大,不适用能量有限的无线传感器网络。因此,很多视频传感器网络的研究采用卡尔曼滤波方法来进行目标跟踪。Medeiros H,Park J,和Kak A[5]提出了一种分簇的卡尔曼滤波跟踪方法,该方法由于需要进行簇头选举,对于节点位置分布有一定的要求,灵活性较差。Soto C,Song B等人[6]提出了一种分布式估计算法即卡尔曼一致性滤波方法,该方法通过相邻节点的跟踪数据交换融合来到达对目标状态的一致性估计。另外,为了优化估计Kamal A T和Farrell J A[7,8]提出了针对测量信息权重分布式最大后验参数的一致性滤波(information weighted consensus filtering,ICF),该方法采用信息矩阵进行节点间的数据融合来达到一致性状态估计,通信数据量虽然比传递图像小,但依然比较耗能。上述方法均没有考虑到节点的通信能耗,因此,通信数据没有进行压缩。Ribeiro A,Giannakis G和 Roumeliotis S[9]在节点间通过传递新息符号进行目标状态的估计来减少通信量,然而,该方法没有考虑目标状态的一致性数据融合。
为减少节点间的通信能耗同时保证跟踪精度,本文提出一种基于残差编码(RC)的一致性滤波跟踪方法,对信息矩阵采用符号编码策略,从而大量减少视频传感器节点之间数据交换量,延长网络的使用时间。
1 基于残差编码的一致性滤波跟踪算法
1.1 一致性滤波
如图1所示,对于每个视频节点采集到的图像序列Xt,在跟踪的过程中,检测到目标的节点采用卡尔曼一致性滤波器来预测目标下一帧的状态。目标的状态和测量方程为
Xt=AXt-1+BVt-1,
(1)
Zt=HXt+Wt.
(2)
节点间传递的信息向量和矩阵为
(3)
(4)
由卡尔曼滤波式(5)~式(7)可预测目标下一帧状态的估计
(5)
i(n|n-1)=Aii(n-1|n-1),
(6)
i(n|n-1)=Hi(n)i(n-1|n-1).
(7)
1.2 残差编码
一致性滤波是通过在网络里传递信息矩阵ui和Ui来进行数据融合达到对目标状态的全局估计。相对于图像数据来说,数据虽然减少了,但对于多维的目标状态信息,通信量依然很大。采用残差符号编码可以有效减少通信能耗。节点间只传递新信息符号编码,这样可以大大减少通信开销。本文将文献[9]提到的新息符号算法扩展到一致性滤波跟踪场合,提出一种基于残差编码的一致性滤波算法,具体步骤如下:
首先,将状态向量映射到二进制量化
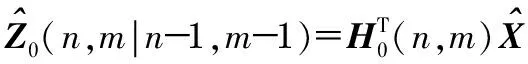
(8)
定义节点i的编码策略为
bi(n,m)=sgn[Z0(n,m)-0(n,m|n-1,m-1)],
(9)
Ki(n,m)=
(10)
i(n|n-1,m)=i(n|n-1,m-1)+
Ki(n,m)bi(n,m),
(11)
Pi(n|n-1,m)=Pi(n|n-1,m-1)-
(12)
然后,通过迭代从1~M,可以得到残差编码消息bi(n)
bi(n)=[b(n,1),…,b(n,M)].
(13)
每一步,相邻节点接收到编码消息bi(n), 通过等式(11)~式(13)从1~M迭代可以得到
(14)
Pi(n|n)=Pi(n|n-1,M).
(15)
最后,可从等式(16)得到一致性状态融合目标状态的估计
(16)
2 多视角数据融合方法
本方法中,检测到目标的各个节点采用高效的基于卡尔曼滤波的目标跟踪算法,并将跟踪的目标信息发送到相邻节点进行数据融合。对多视角跟踪的结果采均值算法进行图像融合,可获得更好的跟踪精度和更长网络使用时间。融合时,必须将目标的像平面坐标[Xt,Yt]映射到地平面坐标[Ut,Vt],其关系由Hj决定
(17)
其中,λ为尺度参数,对于每个视频节点,可计算出目标在地平面的位置
(18)
(19)
通过计算等式(16)等到多个视角跟踪平均融合后的结果。
3 实 验
为了验证该方法的效果,构建基于8个视频节点(CN)的室内测试系统。视频节点分辨率为640像素×480像素,帧速率为25 fps,15 m视野,60°视角;房间面积为6 m×9 m,跟踪持续时间13 s,测试环境和目标运动轨迹如图2所示,初始化参数M=16。
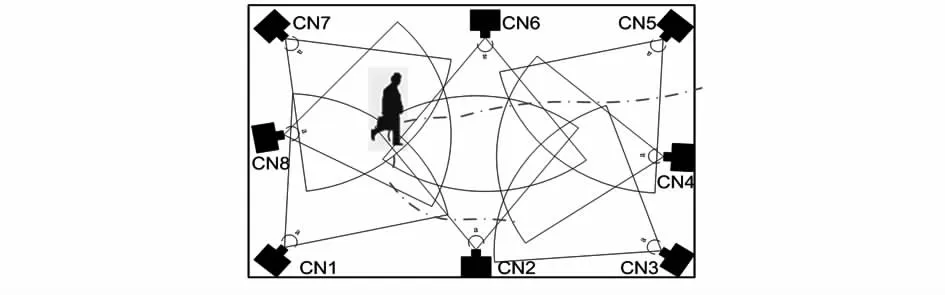
图2 测试环境
在图像序列1~450帧中,视频节点1,2,4,5同时检测到目标,节点1和4的跟踪过程分别如图3(a),(b)所示。

图3 分布式跟踪图示
目标的真实轨迹采用手工标定,目标的跟踪轨迹与单节点1和节点4的观察值之间的比较如图4所示。其中图4(a),(b)为轨迹的比较,图4(c)为一致性滤波器跟踪结果与单节点4滤波跟踪结果的均方根误差(RMSE)比较。从图中可以看出,采用一致性残差编码的方法跟踪精度高于单节点跟踪方法。

图4 跟踪结果
为了评估本文方法的性能,与另外2种分布式跟踪方法进行比较:1)分布式粒子滤波[4](DPF)方法 ;2)卡尔曼一致性滤波[9];该方法通过节点间传递信息向量和方差矩阵来进行一致性状态估计;3)本文提出的方法残差编码一致性滤波(RC—CF)。能耗的结果通过不同目标通过监测区域取10次平均结果。每个算法的数据包大小和计算复杂度如表1所示。
通信的能耗主要由包尺寸即节点间收发的消息量决定。假设目标的位置和速度分别为32位浮点型和16位整型。传统的卡尔曼一致性滤波通过传递4维的状态向量和4×4的方差矩阵来进行节点数据融合。假设每个状态信息通过一个数据包传递。卡尔曼一致性滤波的数据包大小为32×(4+4×4)=640位,而本文方法只需传递(32×4+16)=144位数据。

表1 算法能耗相关因素分析
3种方法的能耗情况如图5所示。可以看出分布式粒子滤波的能耗巨大,这是由于每个节点采用蒙特—卡洛方法进行目标跟踪和数据融合。卡尔曼一致性滤波能耗大约为方法1的30 %,这是由于卡尔曼一致性滤波计算量小。本文的方法为卡尔曼一致性滤波的33 %,主要因为节点间的通信能耗通过残差编码减少的70 %左右。

图5 能耗比较
4 结 论
本文在研究高效分布式跟踪算法的基础上,提出了一种RC—CF跟踪方法,对信息矩阵采用符号编码策略,从而大量减少视频传感器节点之间数据交换量,实验证明:该方法在保证跟踪效果的同时可减少70%左右的能量消耗,从而延长视频传感器网络的寿命。
参考文献:
[1] Karaki Al,Morillo-Pozo Julian.Wireless multimedia sensor networks:Current trends and future directions[J].Sensors,2010,10:6662-6717.
[2] Taj K M,Cavallaro A.Distributed and decentralized multi-camera tracking[J].IEEE Signal Processing Magazine,2011,28(3):46-58.
[3] Tron R,Vidal R.Distributed computer vision algorithms[J].IEEE Signal Processing Magazine,2011,28(3):32-45.
[4] Coates M.Distributed particle filters for sensor networks[C]∥Information Processing in Sensor Networks,2004:99-107.
[5] Medeiros H,Park J,Kak A.Distributed object tracking using a cluster-based Kalman filter in wireless camera networks[J].IEEE Journal of Selected Topics in Signal Processing,2008,2(4):448-463.
[6] Soto C,Song B.Distributed multi-target tracking in a self-configuring camera network[C]∥Computer Vision and Pattern Recogniton,Miami,FL,2009:1486-1493.
[7] Song B,Kamal A T,Soto C,et al.Tracking and activity recognition through consensus in distributed camera networks [J].IEEE Trans on Image Processing,2010,19(10):2564-2579.
[8] Kamal A T,Farrell J A,Roy-Chowdhury A K.Information weighted consensus[C]∥IEEE Conf on Decision and Control,2012:102-115.
[9] Ribeiro A,Giannakis G,Roumeliotis S.SOI-KF:Distributed Kalman filtering with low-cost communications using the sign of innovations[J].IEEE Trans on Signal Processing,2006,54(12):4782-4795.
