机动能力受限的目标-攻击-防御定性微分对策

梁 丽 王佳楠 王春彦 邓 方

1.北京化工大学信息科学与技术学院 北京 100029 2.北京理工大学宇航学院 北京 100081 3.北京理工大学自动化学院 北京 100081

世界各国家军备竞争不断加剧, 随着导弹防御系统的不断完善化和系统化, 导弹的突防问题也成为了国内外学者研究的焦点, 期望导弹具有突破敌方导弹防御系统的能力与其进行对抗, 并对目标进行精准的打击[1-6]. 导弹突防问题是一个由攻击弹、目标、拦截弹组成的三体博弈问题, 称之为目标-攻击-防御（target-attacker-defender, TAD）问题[7-9]. 其中,目标要躲避攻击弹的攻击, 攻击弹的目的是攻击目标且避免被拦截弹拦截, 拦截弹的目的是拦截攻击弹以保护目标避免被攻击弹攻击, 目标与拦截弹合作组成一个团队与攻击弹进行对抗.

TAD 应用情景最早见于文献[10]. 近年来, TAD问题引起了国内外学者的广泛关注[11-14]. 文献[15]提出了一种防御制导导弹为保护空中目标对抗来袭自寻的导弹的协同制导律, 设计了一个多模型自适应估计器（multiple model adaptive estimator, MMAE）来识别输入导弹的导引律和参数, 利用空中目标和防御导弹之间的合作来优化制导律；文献[16]从追逃微分对策的角度, 在局中人动态特性线性化的基础上,假设来袭导弹采取比例导引、增广比例导引或最优制导的具体极限情况；美国莱特-帕特森空军基地的Pachter 教授等从定量微分对策的角度分析了TAD 问题[17-18]. 上述研究都是从定量的角度给出局中人的策略, 没有研究定性微分对策的求解.

文献[7]提出了攻击者角色切换策略与目标-防御者的合作策略；文献[8]综合考虑导弹突防成功率和对目标打击精度的需求, 基于质点模型在二维平面中构建了TAD 问题的统一模型, 并求解了TAD 定性微分对策, 给出了对策的解析解. 然而, 在导弹攻击舰船的实际场景中, 攻击弹、拦截弹和舰船并不在一个运动平面中, 因此, 需要研究不同运动平面中的导弹突防成功的条件和突防策略.

本文将不同运动平面的三人问题抽象成一个目标机动能力受限的TAD 问题, 重点分析目标带有运动约束TAD 问题的特点, 运用TAD 微分对策的求解思路结合阿波罗尼奥斯圆原理, 研究目标机动能力受限的TAD 微分对策定性求解方法, 给出攻击者突防成功的条件和突防策略.

1 问题描述

本文针对机载反舰导弹突防策略展开研究. 攻击弹（攻击者attacker）对一个具有机动能力和防御能力的舰船（目标target）进行打击, 该舰船在意识到导弹攻击威胁时机动躲避, 同时自身或请求友邻平台发射一枚防御弹（防御者defender）拦截攻击弹, 攻击弹要突破防御弹的拦截实现对舰船目标的打击. 攻击弹、舰船和防御弹三者构成一个TAD 三体博弈问题. 为了概念一致, 下文用目标、攻击者和防御者来描述.

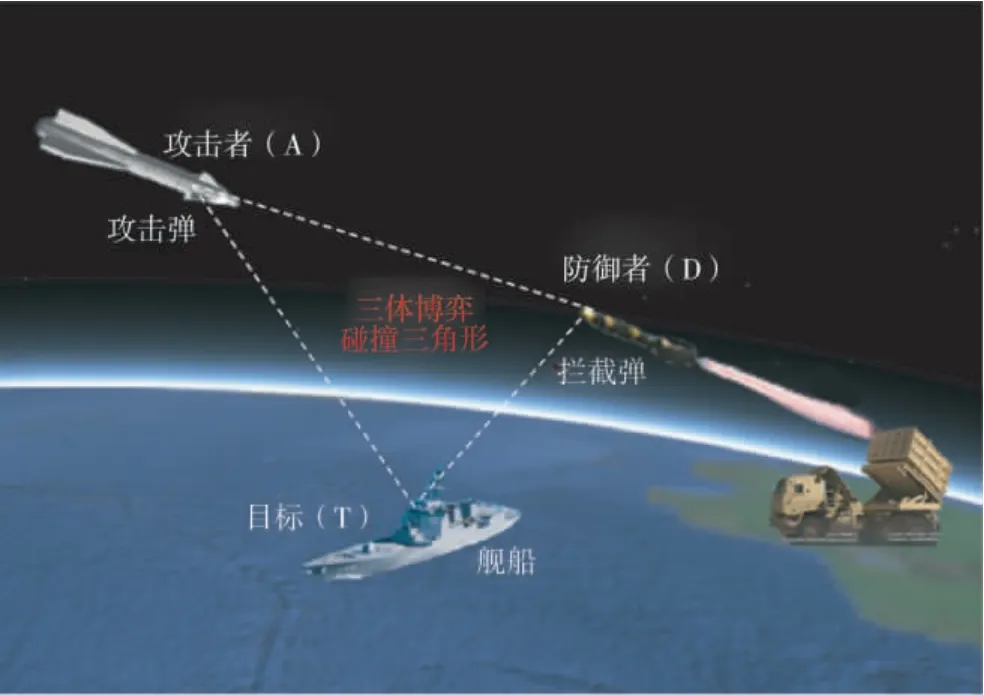
图1 反舰导弹攻防示意图Fig.1 Schematic diagram of anti-ship missile engagement

1.1 TAD 微分对策的数学模型

系统的初始状态为

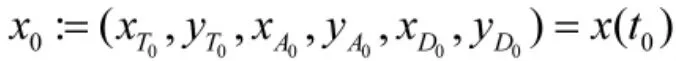
攻击者和防御者在空中运动, 而目标在海平面运动, 为了求解TAD 三体博弈问题, 假设攻击弹和防御弹的运动平面与目标的运动平面相交于一线, 目标只能在此相交线上移动, 即航向角=0°或180°. 如图2 所示. 因此, 这是一个目标机动能力受限的TAD三体博弈问题.

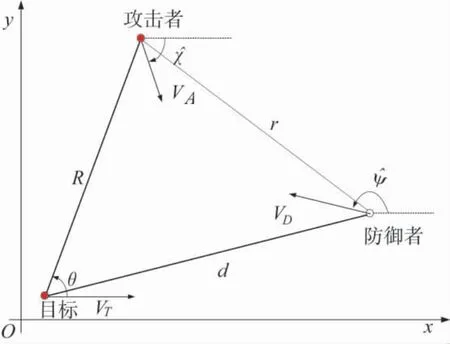
图2 目标运动能力受限的TAD 微分对策Fig.2 TAD differential game with limited target motion ability

1.2 终止条件（目标集）

攻击者目的在于追捕目标的同时避免被防御者拦截, 而防御者试图在适当的时机捕获攻击者, 以防目标被攻击者捕获. 因此, 攻击者的目标集表示为

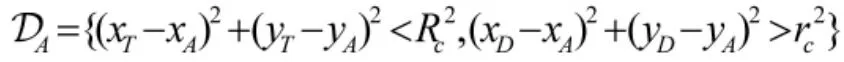
其中, RC和rC为正常数, 分别表示攻击者和防御者的捕获半径. 如果攻击者与目标之间的距离小于攻击者的捕获半径RC, 攻击者成功捕获目标；如果攻击者与防御者之间的距离小于防御者的捕获半径, 防御者成功捕获攻击者.

目标的目标集为

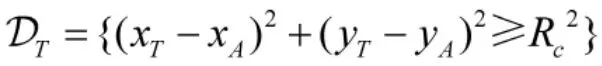
防御者的目标集为

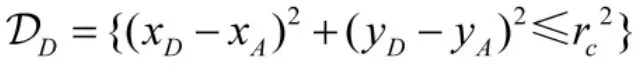
显然, 在TAD 微分对策中存在3 个目标集边界,传统的求解倒退轨迹方程法无法求解这个定性微分对策, 因此, 本文应用阿波罗尼奥斯原理结合几何分析法求解攻击者突防成功的条件.

2 TAD 微分对策定性求解

2.1 阿波罗尼奥斯圆原理

首先考虑攻击者和防御者之间的博弈问题, 引入阿波罗尼斯圆（Apollonius circle）的概念, 阿波罗尼斯圆是一个到平面上两点的距离之比为常数且不等于1 的点的轨迹, D（xD, yD）和A（xA, yA）分别是防御者D 和攻击者A 的位置, 阿波罗尼斯圆O1为点P 的轨迹, 使得为常数, 且β>1. 由几何分析,可求出圆心的坐标为

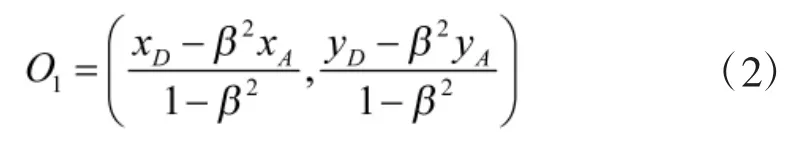
半径为

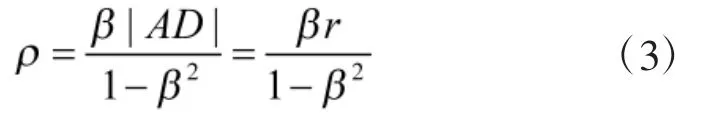
对于一个无界区域内的单对单追逃博弈（PE 博弈）, 当两个博弈者都以简单质点模型运动时, 通过构造阿波罗尼奥斯圆可以得到博弈的完全解[19-20]. 因此, 给出如下定义.

定义1 设P 和E 是追逃博弈中的两个局中人,空间中P 能比E 先到达的所有点W（x, y）所组成的集合, 称之为P 的优胜区域, 记为ΩP.

2.2 攻击者赢得条件

防御者和攻击者构成一个追逃博弈, 其中, 防御者是追捕者, 攻击者是逃跑者. 攻击者A 和防御者D之间的阿波罗尼奥斯圆用O1表示, 圆O1内部为防御者D 的优胜区域, 外部为攻击者A 的优胜区域, 如果A 朝向圆O1内运动, 必然会被防御者D 拦截, 因此,根据阿波罗尼奥斯圆原理, 如果目标T 总能在防御者D 的优胜区域里, 目标T 就能逃离攻击者A 的攻击或者使得防御者D 成功拦截到攻击者A, 因此, 攻击者A 要想赢得对策, 必须在目标T 进入防御者D的优胜区域之前攻击到目标T. 攻击者A 攻击到目标T 的位置点正好在攻击者A 与防御者D 的阿波罗尼奥斯圆上是双方对抗是否成功的临界条件. 因此, 给出如下定理.

定理1 如果系统初始状态满足条件

证明：

目标T 的可达区域是目标T 在被攻击者A 捕获前所能到达的轨迹点, 由于目标T 只能沿直线运动,如果不考虑防御者的拦截, 攻击者A 会在目标T 的运动线上将其捕获.

假设攻击者和目标经过时间△t 后分别从各自的初始位置移动到点C, 如图3 所示.

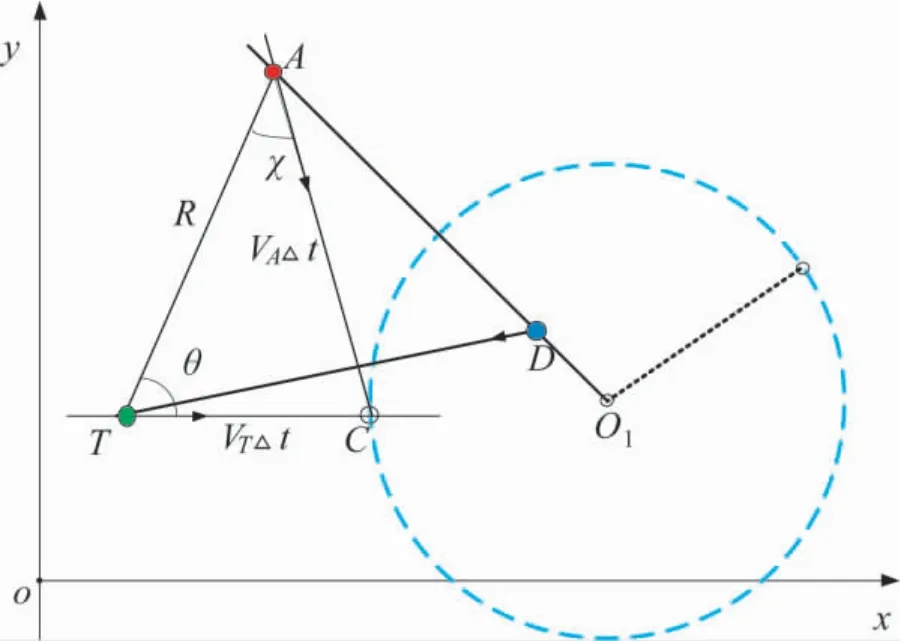
图3 攻击者的优胜区域Fig.3 The dominant area of the attacker

根据三角定理有如下方程

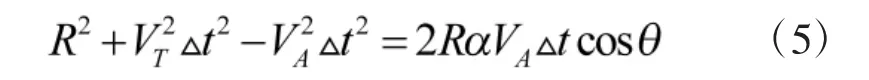
设攻击者A 和目标T 之间的速度比为α, 有

根据余弦定理有

将式（6）和式（7）代入式（5）有

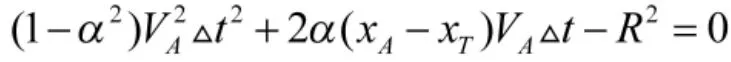
计算得出

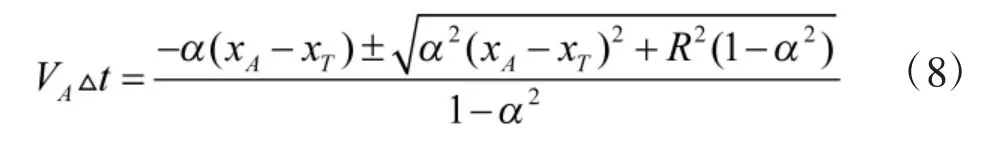
那么C 点坐标可写为

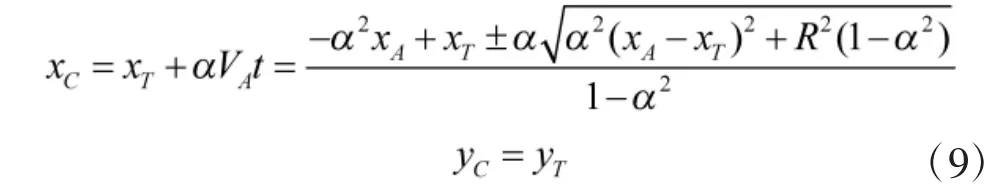
如果C 点处于攻击者的优胜区域, 攻击者就可以在被防御者拦截之前攻击到目标, 因此, 攻击者捕获目标赢得对策的条件可以表示为

将式（2）和式（9）代入式（10）可得到式（4）.

注：攻击者的赢得条件（4）事实上就是目标-攻击-防御微分对策的界栅, 它将整个对策空间分成两部分, 当对策的初始条件满足条件（4）时, 攻击者能赢得对策, 当条件（4）不满足时,防御者和目标赢得对策.

为了直观地显示和理解界栅, 在坐标系中绘制这个边界条件, 假设目标和防御者之间的距离r 为10, 目标T 和防御者D 的坐标分别为xT=（0, 0）和xD=（10, 0）, 攻击者A 的坐标为xA=（x, y）. 图4 显示了界栅与相对参数变化之间的关系, 曲线内部（除D 点外）是攻击者的赢得区域, 曲线和曲线外部是目标-防御者团队的赢得区域. 攻击者赢得区域的大小与目标防御者之间的距离r 成正比, 与速度比参数α 和β 成反比. 当参数β 和r 不变时, α 越大, 攻击者的赢得区域越小, α 越小, 攻击者的赢得区域越大（如图4（a）所示）. 当参数α 和r 不变时, β 越大, 攻击者的赢得区域越小, β 越小, 攻击者的赢得区域越大（如图4（b）所示）.

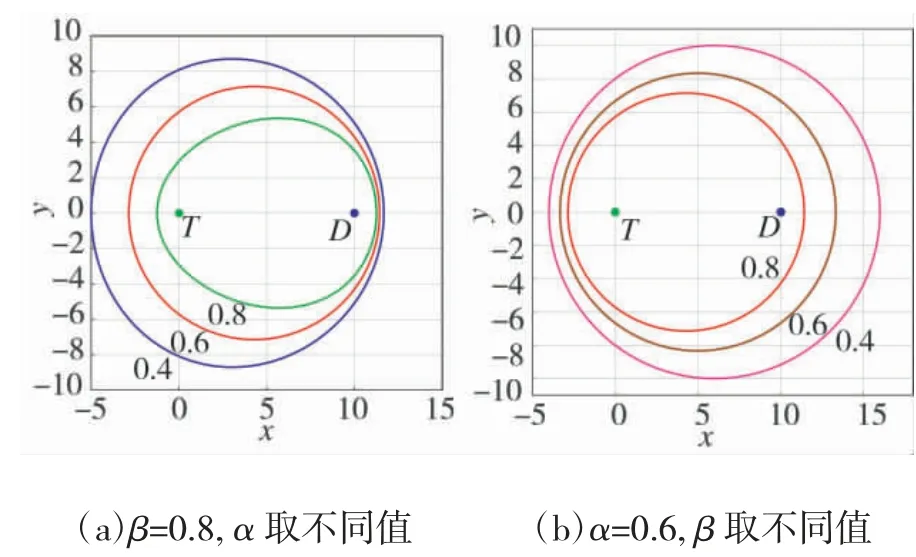
图4 不同参数对应的攻击者的赢得区域Fig.4 The dominant area of the attacker corresponding to different parameters

如图5 所示, 红色曲线为本文目标机动能力受限条件下的界栅, 绿色曲线为文献[6]中目标机动能力不受限时的界栅, 曲线内部为攻击者的赢得区域,曲线外部为防御者和目标的赢得区域, 显然, 当目标的运动能力受限时, 攻击者的赢得区域会相应增加,与实际情况相一致.

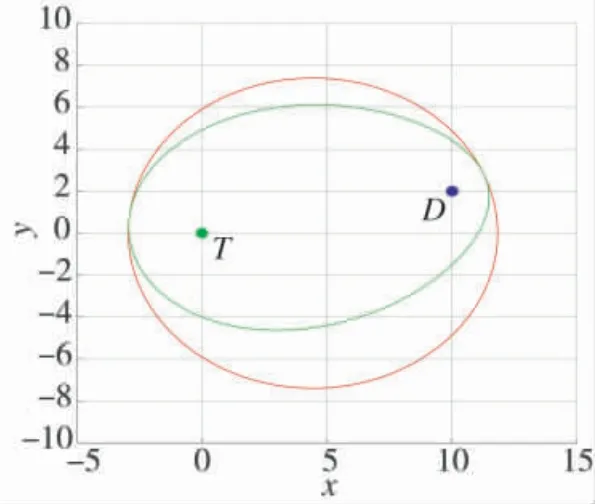
图5 攻击者的赢得区域对比xT=（0, 0）, xD=（10, 2）, α=0.6, β=0.8Fig.5 The comparison of the attacker’s dominant area xT=（0, 0）, xD=（10, 2）, α=0.6, β=0.8

3 目标-攻击-防御微分对策定量求解

当系统状态位于攻击者的赢得区域时, 无论目标-防御者团队采取何种策略, 攻击者总能捕获目标.这种情况下, 攻击者的目的是在最短时间内捕获目标, 相反地, 目标-防御者团队的目的是尽可能延长目标被捕获的时间, 因此, 这个区域中的支付函数可以定义为

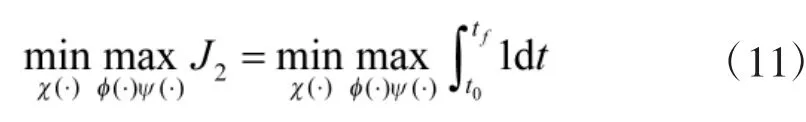
其中, tf为定量目标-攻击-防御微分对策的支付.

自然地, 引入哈密顿函数, 有

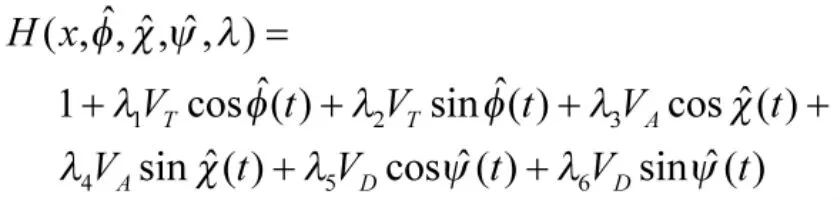
含有协态变量的最优控制输入可以表示为:

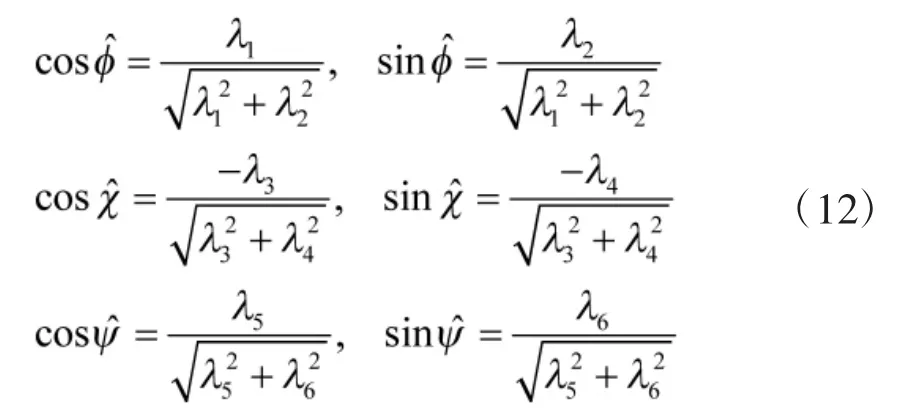
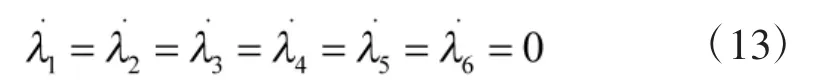
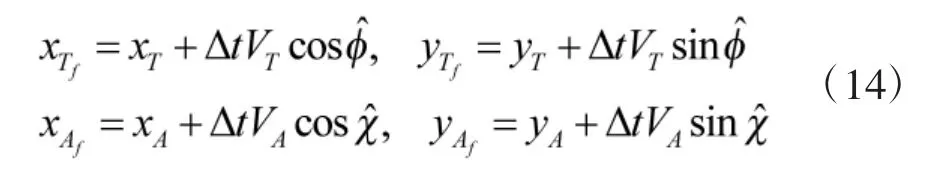
在攻击者的赢得区域, 目标最终会被攻击者捕获, 终止条件可以表示为

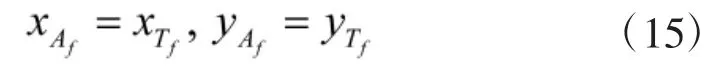
将式（8）和式（14）代入式（15）

可以得到攻击者的最优控制角

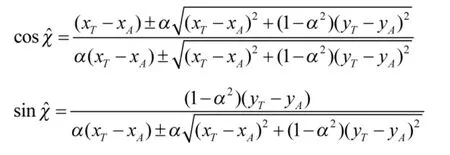
4 仿真实验分析

本节将通过两个仿真示例来说明本文提出的界栅和最优攻击策略的有效性.

攻击者和防御者的初始位置设为：xT0=0 km 和0 km, 攻击者的速度设为10 km 和2 km, 速度比α=0.6, β=0.8.

当攻击者的初始位置位于攻击者的赢得区域时,设xA=（4,7）.攻击者在位置（4.2 km,0 km）处攻击到目标, 打击成功, 耗费时间为140 s, 如图6 所示.

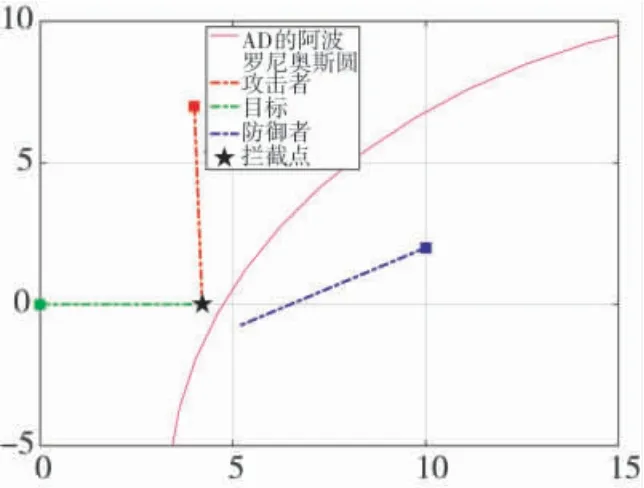
图6 攻击者成功打击目标Fig.6 The attacker successfully attacked the target

当攻击者的初始位置处于赢得区域外围时, 设xA=（5,8）, 防御者在位置（4.8 km,1.5 km）处拦截到攻击者, 成功保护目标, 耗费时间为130 s, 如图7 所示.

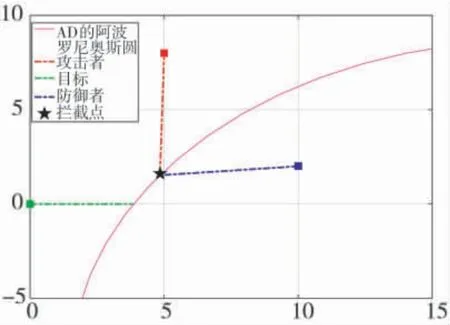
图7 防御者成功拦截攻击者Fig.7 The defender successfully intercepted the attacker

5 结论

针对导弹攻击具有防御导弹保护和机动躲避能力的目标的三体博弈问题, 将不同运动平面的三人问题抽象成一个目标机动能力受限的目标-攻击-防御微分对策问题, 构建了攻击弹、防御弹和机动能力受限目标的三人微分对策模型, 运用显示策略法结合阿波罗尼奥斯圆原理, 求解了目标机动能力受限的目标-攻击-防御定性微分对策, 给出攻击者突防成功的条件和最优突防策略的解析解, 为导弹突防打击提供火力分配和制导策略的决策依据.