永磁同步电机直接转矩控制高速运行范围拓宽

林斌， 孙丹， 贺益康

(浙江大学电气工程学院，浙江杭州 310027)

由PMSM的转矩和定子磁链公式(2)、式(3)可知，每一组(id、iq)都将对应一组(Te、ψs)，因此可得到PMSM DTC在MTPA算法下的转矩与定子磁链的关系，如图3中L1段所示。图3为不同算法下的转矩－定子磁链关系图。可看出，MTPA运行阶段转矩随定子磁链的增大而增大。

点A是MTPA曲线与电流限制圆的交点，若在该点上运行，PMSM可在保持定子电流为最大值条件下输出最大转矩。将式(11)中Is取值为Imax，可得A点所对应的电流、转矩、定子磁链为

0 引言

直接转矩控制(direct torque control，DTC)在定子坐标系中实施运算，无需坐标旋转变换及转子位置信息，具有结构简单，转矩动态响应快，参数鲁棒性强等诸多优点，作为一种高性能的交流电机控制策略，其研究得到了学术界和工业界的广泛关注［1－6］。

然而基于开关表和滞环控制器的常规DTC方式，存在转矩波动大、开关频率不固定等缺点［1］。已有大量文献对其进行了改进研究，提高了系统稳态精确度［2－6］。其中文献［2－3］将空间电压调制(space vector modulation，SVM)方法引入永磁同步电机(permanent magnet synchronous motor，PMSM)常规DTC中，虽系统复杂度略有增加，但实现了开关频率固定，极大提高了系统稳态精确度，也保持了快速的动态响应性能，被广泛认可。但对于PMSM的大量DTC改进研究都是在基速以下，较少涉及弱磁高速运行。

DTC方式下PMSM的弱磁高速运行理论源自矢量控制(vector control，VC)下的弱磁运行。PMSM弱磁高速运行时应满足电压和电流的限制，有文献分别讨论了在该限制条件下PMSM基于VC的最大转矩电流比(maximum torque per ampere，MTPA)［7］、恒 功 率 转 速 比(constant power speed range，CPSR)［8］、最大转矩电压比(maximum torque per voltage，MTPV)［8］等3种运行方式，以期实现最大转矩及高速的运行目标。VC是通过对定子电流矢量的交、直轴分量进行独立(解耦)控制而实现的，DTC则是通过对转矩和定子磁链的控制来实现的。由于PMSM的转矩、定子磁链与交、直轴电流分量有相互对应关系，据此文献［9］讨论了基于DTC的MTPA和CPSR弱磁方法。也有文献指出在电流限制条件下PMSM DTC弱磁运行时，如转矩角超过最大允许值，可能会导致电机运行失步，无法实现PMSM的高速稳定运行［9－10］。

按照VC方式直接推得的DTC弱磁控制算法在转矩和定子磁链计算时需用到交、直轴电感和永磁体磁链，对电机参数的依赖很大。因而需探求一种结构简便、参数鲁棒性更好的控制方法。文献［11－12］提出了一种新颖的电磁转矩给定值的计算方法，但需用到三相静止坐标系到两相旋转坐标系的旋转变换，计算量较大。

为解决DTC方式下PMSM的运行稳定性问题，本文将首先系统地分析MTPA、CPSR和MTPV 3种算法下PMSM的运行状态，指出高速稳定运行的关键。其次在常规SVM－DTC策略的基础上，提出一种转矩角限幅方法，以拓宽电机稳定运行的速度范围。进一步还提出一种利用定子磁链和电流的转矩给定值计算方法，确保了PMSM DTC的高速稳定运行，有效提高了系统鲁棒性，并使电机稳定运行不再受转矩角的影响。详尽的仿真研究结果验证了DTC方式下PMSM的两种拓宽高速稳定运行区域的方法的可行性和有效性。

1 PMSM的运行阶段及转矩角分析

PMSM在不同坐标系下的矢量图如图1所示。在转子磁链定向的d-q同步旋转坐标系下，PMSM的电压、定子磁链、电磁转矩方程可分别表示为

其中:Vd、Vq、id、iq、Ld、Lq、ψd、ψq分别是d、q轴电压、电流、电感和定子磁链;ψs、ψf分别是定、转子磁链;Te是电机的电磁转矩;R是定子绕组的电阻;ω是转子的电角速度，即d-q坐标系的旋转角速度;p是电机的极对数。

由逆变器驱动运行的永磁同步电机存在电流和电压的极限约束条件，即有电流和电压极限方程为

其中:Imax为允许的最大定子电流;Vmax为允许的最大定子电压，一般由逆变器直流母线电压Vdc决定，即Vmax=Vdc/。

式(5)和式(7)表明，电流极限方程可在以id为X轴，iq为Y轴的坐标系内形成一个以O1(0，0)为圆心、Imax为半径的圆;电压极限方程也可画成一个以O2(－ψf/Ld，0)为圆心、长短轴与Vmax/ω成正比的椭圆;上述电流限制圆和电压极限圆如图2中所示。随着转速ω的升高，电压极限圆与转速成反比变小。需要说明的是，文中所绘图形均依据下文仿真研究中的嵌入式PMSM参数所得［1］，此类PMSM的特征是电压限制圆的圆心位于电流限制圆之内。

将式(4)带入式(6)，可得

图2 电流电压限制圆与运行轨迹Fig.2 The limit circles of current and voltage and the operation loci

在对PMSM进行控制时，需确保id、iq值在电流和电压限制圆内。当电机转速低于基速时，电压限制圆的半径较大，id、iq的取值只需满足电流限制圆的要求，此时通常采用MTPA［7］算法，确保单位电流下输出最大转矩，其运行轨迹如图2中L1段所示。当电机运行于基速以上时，电机端电压达到极限，为保证在同时满足电流和电压限幅的条件下电机加速运行，则其运行轨迹必须沿电流限制圆逆时针方向运动，即采用CPSR［8］算法，如图2中L2段所示。由式(2)可知，如id反向增大可减弱d轴磁链，同时id幅值的增大也可导致iq减小，使得定子磁链的幅值减小，以弱磁的方式来满足电压极限条件。当电机运行于更高转速时，为获得单位电压下的最大转矩输出，可采用MTPV［8］算法，即沿着电压极限圆缩小的轨迹运行，如图2中L3段所示。可看出，CPSR阶段能同时利用电压和电流的最大极限容量，而MTPV阶段电流并非维持在其极限值，但MTPV阶段的输出转矩将大于CPSR阶段，对此后文将予以证明。

为保证PMSM DTC系统的稳定运行，必须考察其转矩角的变化情况，因此需对PMSM DTC的MTPA、CPSR和MTPV运行方式进行讨论，并对各阶段的转矩角情况进行深入分析。

1.1 MTPA

设电流矢量Is与d轴的夹角为γ，有其中，Is为电流矢量Is的幅值。则电磁转矩方程可改写为

在电流极限约束条件下，要求单位电流输出最大转矩，可对式(9)求导并整理可得

由PMSM的转矩和定子磁链公式(2)、式(3)可知，每一组(id、iq)都将对应一组(Te、ψs)，因此可得到PMSM DTC在MTPA算法下的转矩与定子磁链的关系，如图3中L1段所示。图3为不同算法下的转矩－定子磁链关系图。可看出，MTPA运行阶段转矩随定子磁链的增大而增大。

点A是MTPA曲线与电流限制圆的交点，若在该点上运行，PMSM可在保持定子电流为最大值条件下输出最大转矩。将式(11)中Is取值为Imax，可得A点所对应的电流、转矩、定子磁链为

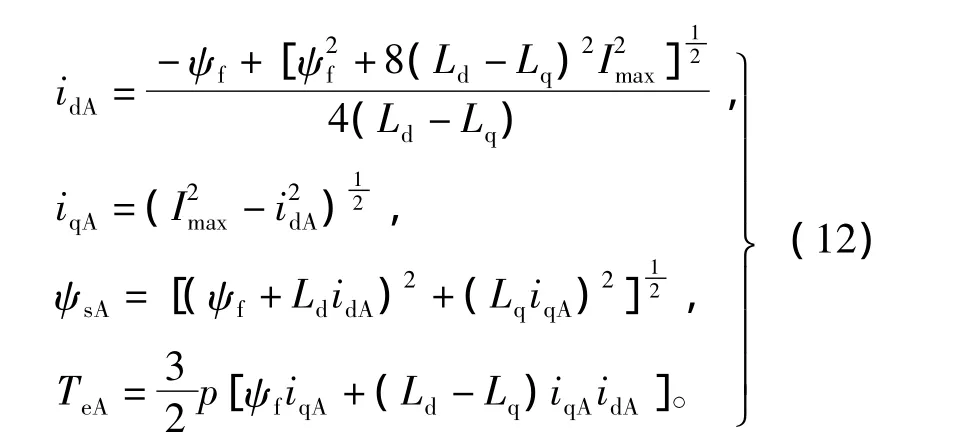
由电压极限方程可知，电压极限圆随着转速的增大而变小。当转速ω小于基速ωb时，电机运行仅需考虑电流限制圆，在A点运行满足电流限制条件，并可输出最大转矩。而当ω增大，电压限制圆逐渐变小将与电流限制圆交于A点，此时需同时考虑电流与电压的限制要求。

1.2 CPSR

当转速上升到基速ωb、定子端电压也达到最大值Vmax，id、iq的取值必须同时满足电压和电流极限条件。将式(5)和式(7)2个不等式取等号求解可得

同理，根据式(2)、式(3)可得CPSR算法下的转矩与定子磁链的关系，如图3中L2段所示，图中ω2＞ω1＞ωb。可看出，转矩和定子磁链均随着转速的提高而减小，符合弱磁运行时的电机特性。

1.3 MTPV

当电机超过某一转速后，任一给定转速下，电动机电压极限圆轨迹上存在着一输出转矩最大的点。

根据式(7)，可得

其中，θ为一角度变量。

则电磁转矩可改写为

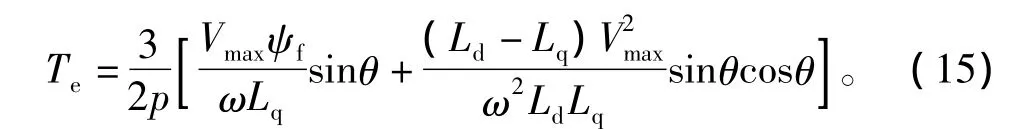
对式(15)求导，并整理可得

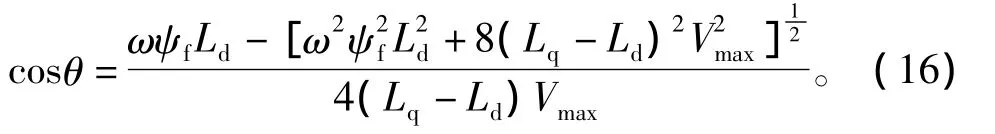
令cosθ=λ，则有

同理，由式(2)、式(3)可得MTPV算法下的转矩与定子磁链的关系，如图3中L3段所示。

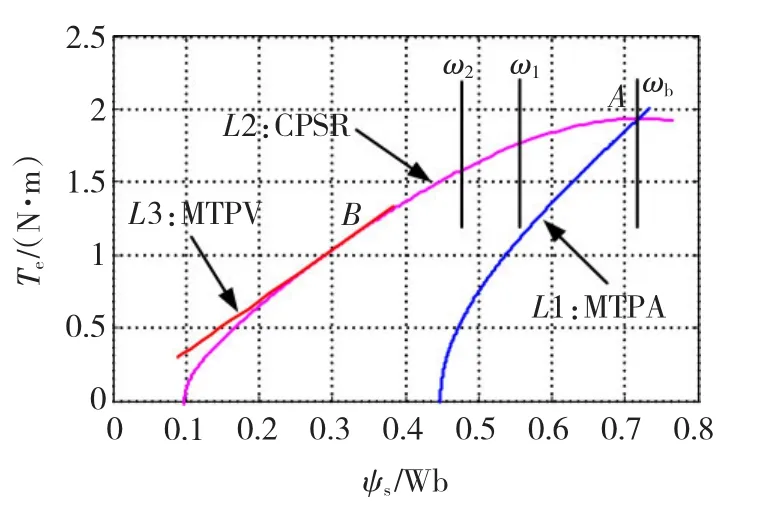
图3 转矩－定子磁链关系图Fig.3 Relationship between torque and stator flux linkage

可看出图3中的L3段与L2段相交于B点，即MTPV曲线与电流限制圆的交点，与图2对应。可发现在相同的定子磁链条件下L3段的转矩大于L2段，说明如在B点之后选择MTPV算法，则可在满足电压电流限制条件下输出更大的转矩。

1.4 转矩角

PMSM电磁转矩方程可用定、转子磁链的关系表示为

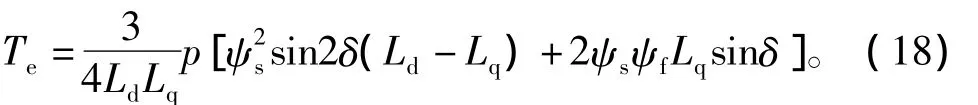
其中，δ为转矩角，即定、转子磁链矢量间的夹角。对式(18)求导得

在PMSM DTC系统中，当δ＜δm时转矩值将随转矩角的增大而增大，当δ=δm时转矩达最大;而当δ＞δm时转矩值将随着δ的增大而减小，最终将会导致转矩关系不平衡而使电机运行失步。因此弱磁控制时为保证系统运行稳定必须保持δ≤δm。

根据式(18)可知，Te、ψs、δ 3者中只有2个独立，因此在已知MTPA－CPSR－MTPV 3个阶段中Te随ψs变化轨迹的前提下，可绘制出δ随ψs变化的轨迹，如图4所示。图中L1段为MTPA，L2段为CPSR，L3段为MTPV。同时由式(20)还可得到最大转矩角δm随ψs变化的关系，如图4中L4段所示。

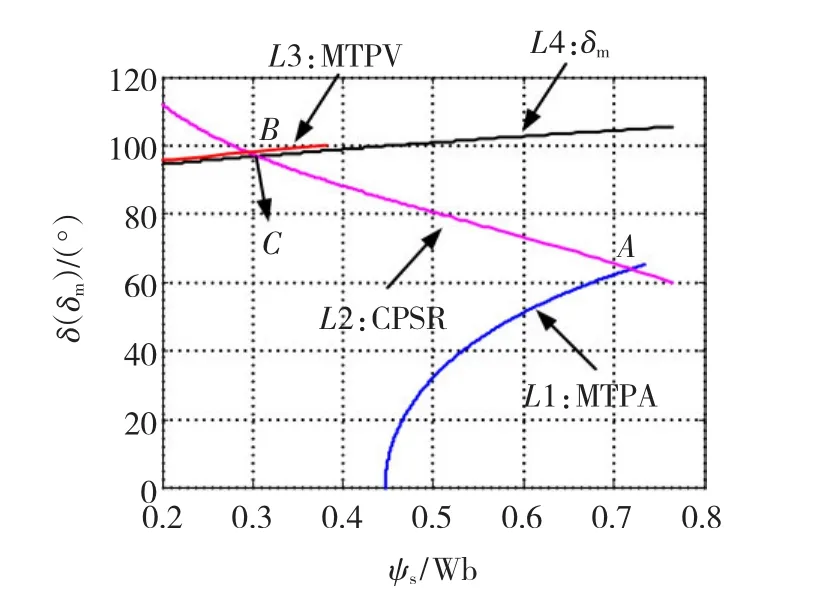
图4 转矩角(最大转矩角)－定子磁锭关系图Fig.4 Relationship between torque angle(maximum torque angle)and stator flux linkage

由图4可知，在整个MTPA阶段δ均小于δm;在CPSR阶段随着转速的不断上升ψs逐渐减小，δ随之增大，而 δm随之减小。在 ψs=0.306 Wb，δm=96.97°的C点，δ等于 δm，C点之后 δ超过 δm导致CPSR运行区域出现不稳定。而在MTPV整个阶段的转矩角δ始终大于最大转矩角δm，无法稳定运行。因此为了使PMSM DTC系统速度运行范围得到拓展，必须进行必要的改进。

2 PMSM SVM-DTC弱磁运行的实现

传统PMSM SVM－DTC的结构框图如图5所示［2］。其中，转矩与定子磁链给定值计算模块如图6所示。当ω ＜ωb，输出转矩最大值为图3中A点所对应的转矩。而当ω＞ωb之后，受制于电压极限，转矩将无法维持该最大值。根据图3，CPSR运行阶段每一转速将对应一个最大输出转矩，且其值随转速的升高而降低。据此可制定出一个最大转矩－转速查询表Temax=f(ω)，以对通过转速PI调节器获得的初始转矩给定T'e实现限幅，获得最终的转矩给定值。

图5 传统永磁同步电机直接转矩控制结构框图Fig.5 Block diagram of SVM DTC for PMSM

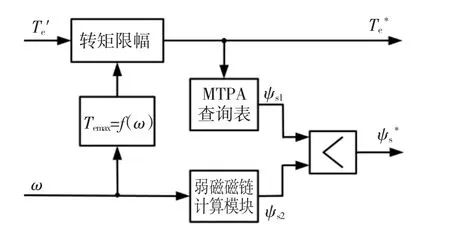
图6 转矩与定子磁链给定值计算模块Fig.6 Calculator of reference torque andstator flux linkage

当ω＜ωb时电机按MTPA轨迹运行，此时可根据转矩与定子磁链的对应关系，通过查询MTPA表格获得转矩给定下所对应的定子磁链ψs1。而当ω＞ ωb之后为满足电压极限要求，根据ψs2=Umax/ω关系，定子磁链需随转速的增大而减小。通常在低速时ψs1小于ψs2，高速时ψs1大于ψs2，此时可通过对ψs1和ψs2的比较，取小值作为定子磁链的实际给定幅值。

由式(18)可知，在定子磁链幅值一定的情况下电磁转矩主要由转矩角来决定。因此可利用PI调节器将转矩的误差反映到转矩角的变化上，继而通过改变定子磁链相对于α轴的夹角来改变参考电压空间矢量的给定值，实现对转矩的有效控制。图7即为定子磁链角度给定值计算模块。

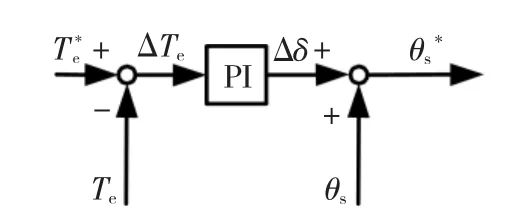
图7 定子磁链角度给定值计算模块Fig.7 Calculator of reference stator flux linkage angle

3 转矩角限幅方法

在基速以上，随着转速的上升定子磁链减小，由图4可见，最大转矩角也变小;但按CPSR算法求得的转矩角却随转速增加而增大。为了保证作为DTC稳定运行依据的PMSM转矩角和转矩之间的正比例关系，满足δ≤δm的稳定运行条件，必须对转矩角实施限幅。通过对图5的观察发现，MTPV阶段的δ略大于δm且与δm非常接近，因此可以在C点之后通过对δ进行限幅而实现类MTPA算法下的高速运行。考虑到传统PMSM SVM－DTC中没有对转矩角进行直接观测和控制，必须对算法进行改进。

由图4可知，最大转矩角δm与定子磁链ψs间存在一一对应关系;而在弱磁阶段定子磁链ψs与转速ω间同样存在对应关系，因此可得到以查询表表示的最大转矩角与转速之间的关系δm=f(ω)，这样就可根据转速ω来确定允许的最大转矩角δm，实现δ限幅控制。

图8为基于转矩角限幅的定子磁链角度给定值计算框图。在通过传统算法得到定子磁链矢量初始给定相对于α轴的夹角θ's后，与电机转速ω积分求得的转子位置角θe比较，得到给定转矩角δ。再通过查表得到允许最大转矩角δm，实现对给定转矩角限幅，按此从转矩的限制角度保证满足稳定运行条件。最后将经限幅后的给定转矩角与转子位置角θe相加，即可作为给定定子磁链相对于α轴的夹角给定值。

图8 基于转矩角限幅的定子磁链角度给定值计算框图Fig.8 Calculation diagram of reference stator flux linkage angle based on torque angle limitation

上述分析表明，通过转矩角限幅之后的PMSM SVM－DTC可在高速时达到类MTPV的运行效果。可见该改进方法的优势是能在不过多增加运算复杂性的前提下，通过对电机转矩角的有效处理，保证电机的高速稳定运行，同时实现了最大转矩输出。但其运行特征与MTPV算法相似，即在转速逐渐上升时保持电机端电压最大，电流幅值随之减小。

4 改进给定转矩计算方法

在传统PMSM的SVM－DTC弱磁运行中，转矩限幅值是根据Temax=f(ω)关系通过查表获得，而该表的建立对交、直轴电感Ld、Lq和永磁体磁链ψf等电机参数的依赖较大，系统鲁棒性较差。同样，基于转矩角限幅的改进策略中也需要用到Temax=f(ω)关系，同样也需依赖精确的电机参数。对此本文进一步提出一种基于定子磁链定向、对电机参数依赖性小的改进转矩给定方法，其算法如图9所示。

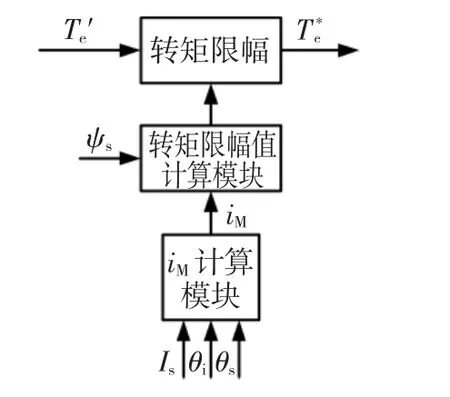
图9 给定转矩改进方法Fig.9 Modified algorithm of reference torque

定子磁链定向即将同步速旋转的M－T坐标系的M轴定在定子磁链矢量方向上，如图1中所示。此时有定子磁链M轴分量ψM=ψs，T轴分量ψT=0。

这样定子磁链定向下电磁转矩方程可表示为

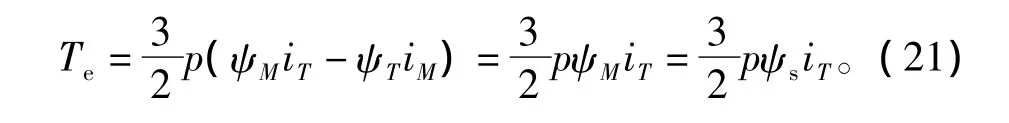
其中，iM、iT分别为定子电流的M轴和T轴分量。

在M－T坐标系下，转矩限幅值可表示为

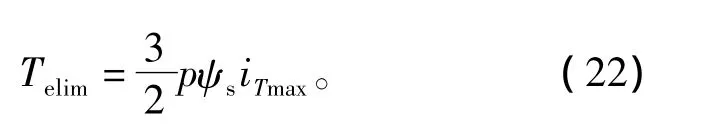
其中，iTmax为下式计算得T轴电流的最大值，可表示为

其中，定子电流M轴分量iM为

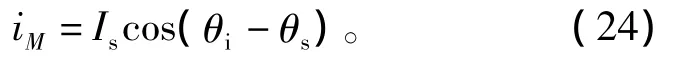
其中:θi为定子电流矢量Is相对于α轴的夹角;θs为定子磁链矢量ψs相对于α轴的夹角，如图1所示。

利用转矩限幅值Telim对转速PI调节器的输出T'e实施限幅，即可得到改进的给定转矩T*e。

上述改进转矩给定算法，利用定子磁链与定子电流在定子磁场方向上分量的乘积获得转矩限幅值，能够实时地根据系统的实际运行状态计算转矩限幅值，不再需要保持转矩角和转矩之间的严格正比例的关系，因此转矩角无需维持在最大转矩角范围内，就可实现高速稳定运行。而且由于改进算法中转矩限幅值与交、直轴电感和转子永磁体磁链没有直接联系，因此对电机参数依赖小，鲁棒性强。

5 仿真研究

为验证上述分析和改进方法的正确性，针对一内嵌式PMSM进行了基于Matlab/SIMULINK的仿真研究，电机参数如下:极对数为2，定子电压18.6 Ω，直轴电感0.388 5 H，交轴电感0.475 5 H，永磁磁链0.447 Wb，最大定子电压240 V，最大定子电流1.4 A，额定转矩1.94 N·m。运行条件为空载启动至转速6 000 r/min，。图10～图12分别是PMSM基于传统SVM－DTC、转矩角限幅SVM－DTC和给定转矩改进SVM－DTC的运行特性。

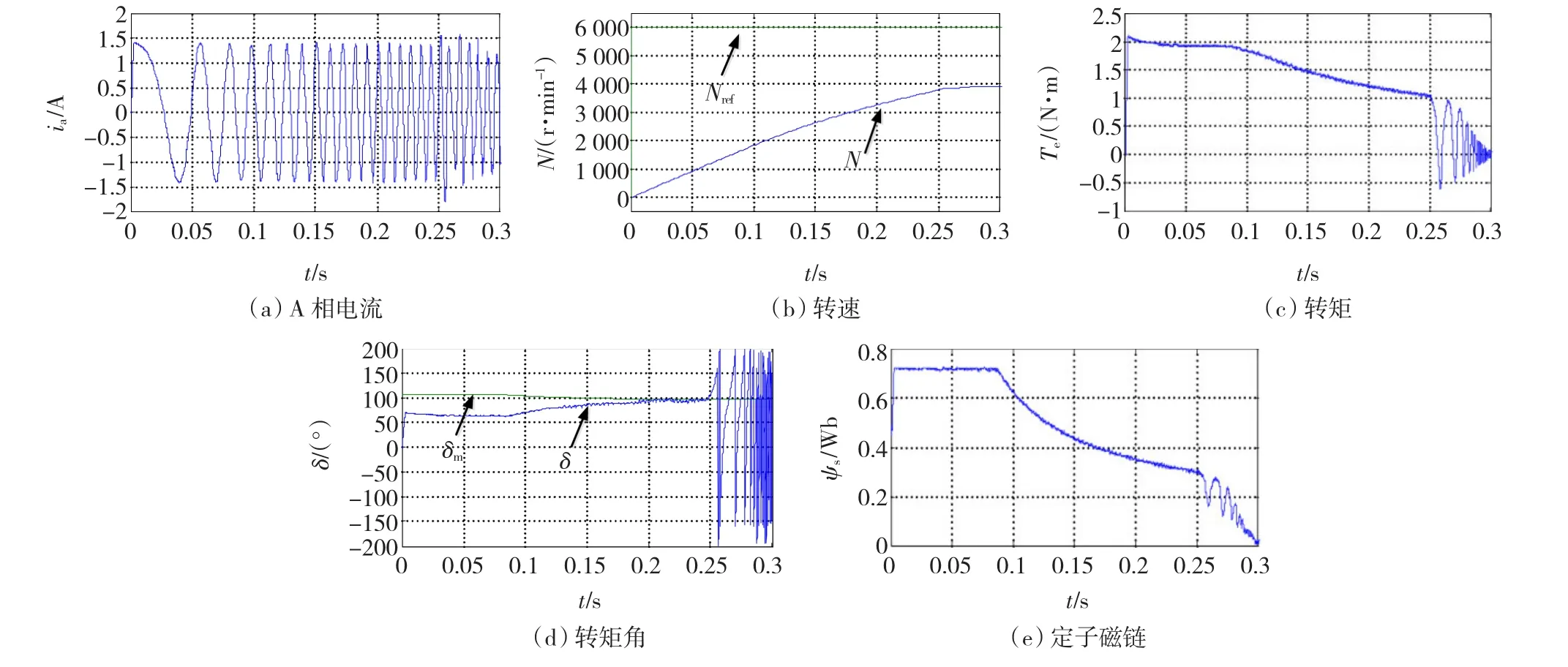
图10 传统PMSM SVM-DTCFig.10 Conventional PMSM SVM-DTC

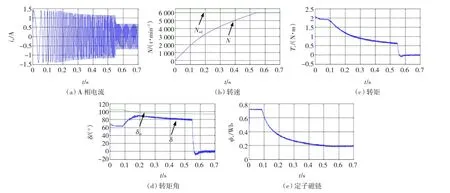
图11 转矩角限幅PMSM SVM-DTCFig.11 PMSM SVM-DTC based on torque angle limitation

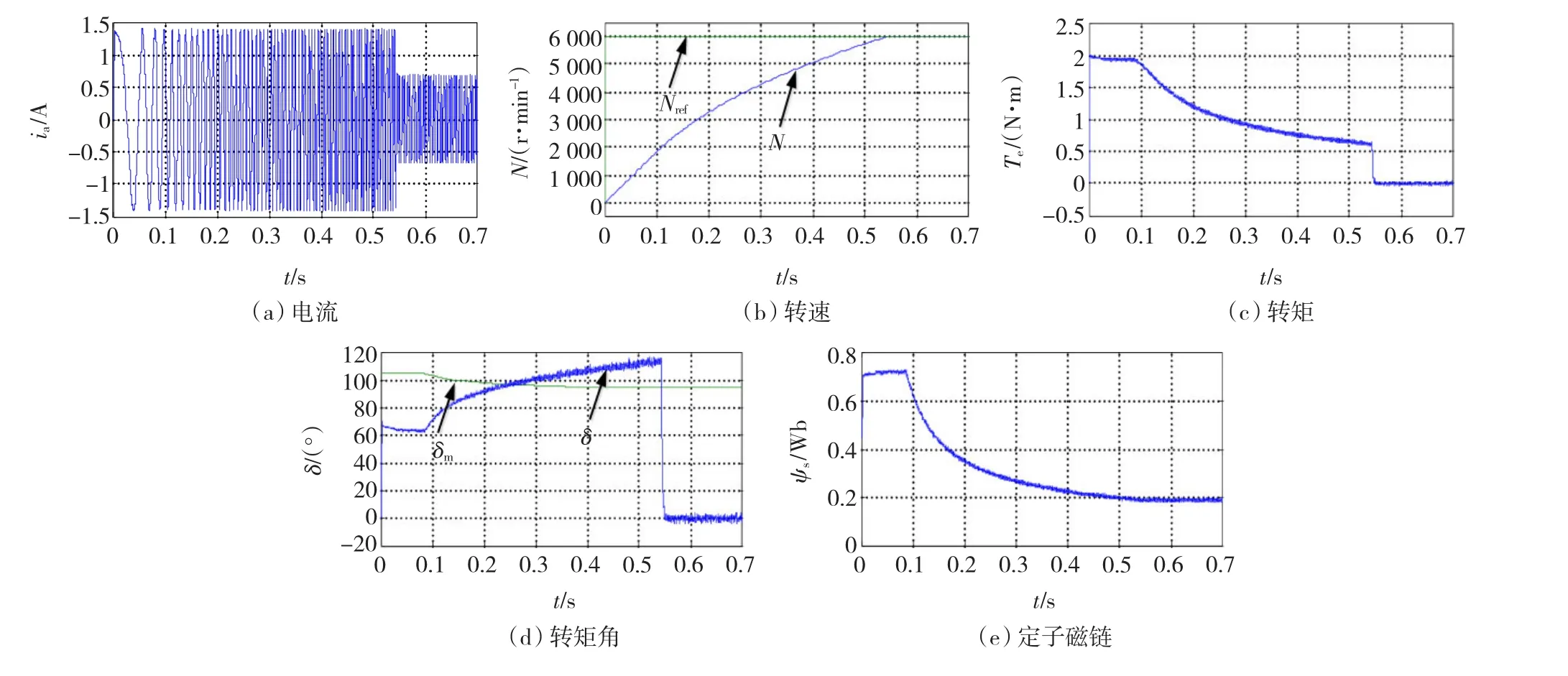
图12 给定转矩改进PMSM SVM-DTC Fig.12 PMSM SVM-DTC based on modified reference torque algorithm

由图10可知，在t=0.25 s之前，基于传统SVMDTC的PMSM运行稳定，电流保持最大幅值，转速平稳升高。升速过程中转矩角一直小于最大转矩角，基速以上磁链开始变小。在t=0.25 s之后电流开始波动，转矩和转矩角振荡剧烈，磁链也在波动。表明此时转矩角已超过了最大转矩角，导致电机运行失步。

图11波形表明，基于转矩角限幅SVM－DTC的PMSM系统，在转矩角达到最大转矩角之前，转速不断上升，转矩角不断增大，电流幅值维持为最大幅值;而在转矩角接近最大转矩角时，由于受到转矩角限幅控制，转矩角变化趋缓，与图4所示的最大转矩角的变化规律一致，最终在转速达到给定值之后转矩角降至零。当转矩角随最大转矩角的限制逐渐减小时，电流的幅值随之减小，与MPTV阶段的运行阶段特性相似。从图中可发现，实际转矩角开始减小的时刻在t=0.2 s，而此时实际转矩角尚未达到最大转矩角。这是因为实施限幅的对象是给定转矩角，而非实际转矩角，故其开始限幅的时刻主要由转矩PI控制器的输出决定，从而导致实际转矩角的提早减小。同时可看出，由于是转矩角开环控制，实际转矩角与最大转矩角之间存在一定差值，即实际转矩角的轨迹不是最大转矩角的轨迹。

由图12可看出，基于给定转矩改进SVM－DTC的PMSM系统，随着转速的升高，转矩角不断增大。同时A相电流幅值始终保持最大，表明此方法充分利用了电机极限容量。而且当转矩角超过最大转矩角之后，系统依然稳定运行。

6 结论

1)系统地分析了PMSM基于MTPA、CPSR和MTPV 3种算法的特点以及转矩角的情况，总结出DTC方式下PMSM弱磁高速运行时转矩角超过其最大值是系统失稳的关键。

2)提出了基于转矩角限幅的DTC方法，可有效限制转矩角，使得PMSM能在转矩角限幅阶段运行于类MTPV算法，获得最大转矩，确保PMSM高速运行时的稳定性。

3)提出了基于转矩给定改进计算方法的DTC策略，能有效提高系统的参数鲁棒性，实现同时满足电流和电压限幅状态下的高速稳定运行，更有效地拓宽了PMSM的高速运行范围。

4)两种方法均可保持PMSM DTC系统优异的动态性能，且计算方便。

［1］ZHONG L，RAHMAN M F，HU W Y，et al.Analysis of direct torque control in permanent magnet synchronous motor drives［J］.IEEE Transactions on Power Electronics，1997，12(3):528－536.

［2］TANG L X，ZHONG L，RAHMAN M F，et al.A novel direct torque controlled interior permanent magnet synchronous machine drive with low ripple in flux and torque and fixed switching frequency［J］.IEEE Transactions on Power Electronics，2004，19(2):346－354.

［3］孙丹，贺益康.基于恒定开关频率空间矢量调制的永磁同步电机直接转矩控制［J］.中国电机工程学报，2005，25(12):112－116.

SUN Dan，HE Yikang.Space vector modulated based constant switching frequency direct torque control for PMSM［J］.Proceedings of the CSEE，2005，25(12):112－116.

［4］裘君，赵光宙.永磁同步电机磁链自适应控制［J］.电机与控制学报，2009，13(6):798－803，810.

QIU Jun，ZHAO Guangzhou.Flux adaptive control of PMSM［J］.Electric Machines and Control，2009，13(6):798－803，810.

［5］贾洪平，孙丹，贺益康.基于滑模变结构的永磁同步电机直接转矩控制［J］.中国电机工程学报，2006，26(20):134－138.

JIA Hongping，SUN Dan，HE Yikang.The PMSM DTC based on variable structure sliding mode［J］.Proceedings of the CSEE，2006，26(20):134－138.

［6］万健如，宫成，刘暐，等.基于MTPA的永磁同步电机滑模变结构直接转矩控制［J］.电机与控制学报，2012，16(3):30－35.

WAN Jianru，GONG Cheng，LIU Wei，et al.Sliding mode variable structure control of permanent magnet synchronous machine based on MTPA［J］.Electric Machines and Control，2012，16(3):30－35.

［7］KWANG Woon Lee，SANG Bin Lee.MTPA operation point tracking control scheme for vector controlled PMSM drives［C］//International Symposium on Power Electronics Electrical Drives Automation and Motion(SPEEDAM)，June 14－16，2010，Pisa.2010:24－28.

［8］MORIMOTO S，TAKEDA Y，HIRASA T，et al.Expansion of operating limits for permanent magnet motor by current vector control considering inverter capacity［J］.IEEE Transactions on Industry Applications，1990，26(5):866－871.

［9］RAHMAN M F，ZHONG L，KHIANG W L.A direct torque-controlled interior permanent magnet synchronous motor drive incorporating field weakening［J］.IEEE Transactions on Industry Applications，1998，34(6):1246－1253.

［10］窦汝振，温旭辉.永磁同步电动机直接转矩控制的弱磁运行分析［J］.中国电机工程学报，2005，25(12):117－121.

DOU Ruzhen，WEN Xuhui.Analysis of field weakening operation for the direct torque control of PMSM［J］.Proceedings of the CSEE，2005，25(12):112－116.

［11］INOUE Y，MORIMOTO S，SANADA M.A novel method of maximum-power operation for IPMSMs in DTC system［C］//13th European Conference on Power Electronics and Applications，September 8－10，2009，Barcelona.2009:1－10.

［12］INOUE Y，MORIMOTO S，SANADA M.Control method suitable for direct-torque-control-based motor drive system satisfying voltage and current limitations［J］.IEEE Transactions on Industry Applications，2012，48(3):970－976.