基于混沌理论的模拟量纠错编码方法研究
2014-09-18马林华贾镇泽
胡 星,马林华,贾镇泽,杨 雪
(1.空军工程大学航空航天工程学院,陕西西安 710038;2.空军驻北京地区军事代表局,北京 100009)
1 研究背景
1.1 数字纠错编码的局限性
1948年,香农(Shannon)在论文《通信的数学原理》中提出并证明了有噪信道编码定理(香农第二定理)。信道编码定理告诉人们:只要信息传输速率小于信道容量,则信息传输可以以任意小的错误概率进行[1]。这一结论为信道编码指出了方向,开创了信道编码的新纪元。
信道纠错编码最开始就是在数字通信中实现的。1950年,汉明发表了纠正单个随机错误的汉明码;随后半个多世纪,在信息技术发展和实际需要的不断推动下,人们一直在寻求纠错性能更好的、简便的编码方法,去逼近Shannon理论的理想界限。从早期的分组码(BCH码、RS码)、卷积码、串行级联码,到今天的Turbo码、LDPC码,其性能在不断逼近Shannon限。
经试验表明:Turbo、LDPC码的性能与香农限只相差不到1 dB[2-3]。由于数字通信在信源压缩、信源加密、信道编码以及数字调制等方面已有成熟技术,因此已在各个领域得到广泛应用。
对于数字图像无线通信来说,关键在于信源压缩和信道编码。在生活中仍存在许多的物理量是模拟的,数字通信需要对信源进行量化,量化是将幅度连续的序列按照一定的准则转变成幅度离散的序列,会产生不可恢复的量化误差[4]。另外,模拟信源在量化后,其传输带宽就会扩展。因此要进行信源压缩,如JPEG、MPEG、H.264等,压缩后的信源包含的冗余信息大大减少,对误码很敏感,会产生误码扩散的问题。例如,近年来视频压缩标准H.264得到了广泛的应用,它的熵编码是基于上下文的算术码CABAC,由于其压缩性能较高,冗余信息留存较少,解码一旦出现错误,比特就会很快地将误码扩散,导致重建视频质量的严重下降[5]。
在数字图像通信中,由于存在量化误差、带宽扩展、误码扩散等问题,传输的误码率只有在低于10-6时,才能保持正常通信。但是在低信噪比的恶劣环境中,现有的成熟的数字编码技术,很难保证误码率低于10-6,使无线图像通信难以进行。
1.2 四位循环Baker码的研究意义
传统的模拟通信,由于没有有效的模拟量信道编码方法,因此抗噪声能力很弱,应用受到限制。当加入模拟量信道编码方法后,模拟通信系统具有抗噪声能力,在无线遥测、通信控制、军事等领域都有很强的应用需求。数字纠错编码通信和模拟量的纠错编码通信模型如图1、图2所示。
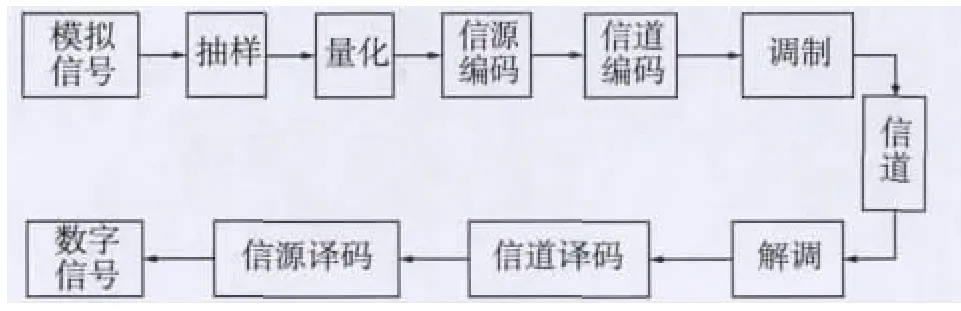
图1 数字纠错编码通信的基本模型
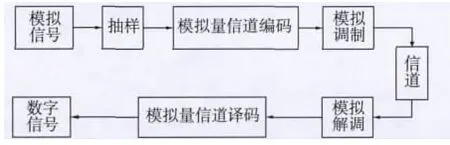
图2 模拟量纠错编码通信的模型
所谓的模拟量信道编码就是在传输模拟信息时,只进行采样,不需要进行量化直接传输。为了进行有效、可靠的模拟量通信,关键在于信源压缩和信道编码。
早在20 世纪80 年代,Wolf和 Marshall[6-7]首次提出了“模拟量纠错编码”的概念。近年来,关于模拟量纠错编码的研究有了一定的进展,模拟量纠错编码的关键在于设计和构造性能好的映射关系,在模拟量编码概念被提出的近30年中,只发现了为数不多的几种具有纠错性能的码字,分为线性和非线性构造方法。例如数字正余弦变换(DCT/DST)码、数字傅里叶变换(DFT)码(其一些码字演化为模拟量BCH码和RS码)等线性码字,以及Kai Xie等人提出的非线性的镜像Baker码(Mirrored Baker’s Map Code)和混沌模拟量拓扑(CAT)码[8]。
对于Kai Xie等人提出的非线性的镜像Baker码,在较高信噪比(10 dB以上)的纠错能力有待于进一步提高。本文借鉴近年“镜像Baker码”模拟量纠错编码研究结果,提出“四位循环Baker码”的编码方法和最大似然译码方法,有效提高了模拟量编码的纠错性能。
2 编码方法的改进
2.1 镜像Baker码编码方法
Kai Xie,Jing Li(Tiffany)提出的镜像 Baker码[9]是基于Baker’s map和tent map结合构造的混沌系统,通过该混沌系统映射获得的一种编码方法。
混沌系统是一种在演变过程中对初始状态具有很强敏感性的非线性系统[10]。近年来,混沌的这种特性被Xie Kai和Li Jing发现,这种对初始状态的敏感性是模拟编码的关键[11]。具体说来,如果把混沌系统的初始状态看作是有待于编码的信源,把混沌系统演变而来的状态看作是编码后的码字,这样混沌系统就可以有效地放大信源的差异,增大码距,从而达到信道编码的目的[12]。另外,为了得到均衡的纠错能力,提出一种镜像的结构来构造码字。其中,{x[0],y[0]}是码字的初始状态,{x[k],y[k]}是根据Baker’s map的映射函数F得到的后续状态,即

通过Baker’s map变换可以进行模拟编码,镜像编码是指对每个二维的信源调换次序,得到镜像的对称信源。例如:对信源{u,v},首先将其作为初始状态进行Baker’s map 变 换,得 到 编 码 码 字 {x1[0],y1[0]}={u,v},{x1[1],y1[1]},{x1[2],y1[2]},…,{x1[2N-1],y1[2N-1]},再对 {v,u}进行变换得到 {x2[0],y2[0]}={u,v},{x2[1],y2[1]},{x2[2],y2[2]},…,{x2[2N-1],y2[2N-1]},得到码率为c的码字。编码过程为

2.2 四位循环Baker码编码方法
本文提出的四位循环Baker码也是利用Baker’s map和tent map结合构造的混沌系统,通过对信息位的扩展,构造出一种四位循环的结构,来平衡各位的纠错能力,再通过该混沌系统的映射,得到四位循环的码字,如图3所示。
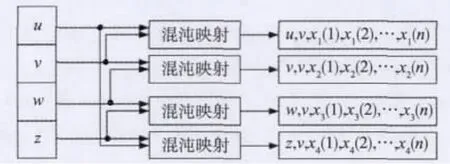
图3 四位循环Baker码编码流程
通过循环结构的编码方式,加强信源的相关性,实现信源的均衡保护,从而提高纠错的性能。例如对信源{u,v,w,z},根据Baker’s map利用循环的方式进行编码。首先,对 {u,v}进行变换得到 {x1[0],y1[0]}={u,v},{x1[1],y1[1]},{x1[2],y1[2]},…,{x1[2N-1],y1[2N-1]},对 {v,w}进行变换得到 {x2[0],y2[0]}={v,w},{x2[1],y2[1]},{x2[2],y2[2]},…,{x2[2N-1],y2[2N-1]},对{w,z}进行变换得到{x3[0],y3[0]}={w,z},{x3[1],y3[1]},{x3[2],y3[2]},…,{x3[2N-1],y3[2N-1]},再对 {z,u}进行变换得到 {x4[0],y4[0]}={z,u},{x4[1],y4[1]},{x4[2],y4[2]},…,{x4[2N-1],y4[2N-1]},得到码率为1/2N的码字。编码过程为
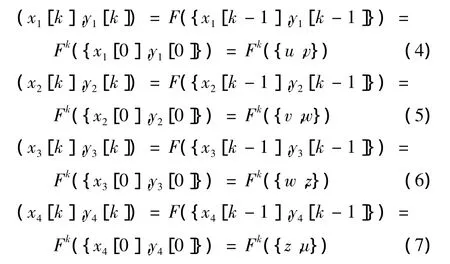
3 最大似然译码
本文提出的四位循环Baker码,利用最大似然准则进行译码[13]。但模拟量的最大似然译码不同于数字的最大似然译码。
对于数字量的最大似然译码准则为:设离散单符号信道的输入符号集为A={ai},i=1,2,…,r;输出符号集为B={bj},j=1,2,…,s;制定译码规则就是设计一个函数F(bj),它对于每一个输出符号bj确定一个唯一的输入符号ai与其对应。即选择一种译码函数F(bj)=a',a'⊂A,bj⊂B,使满足P(bj|a')≥P(bj|ai),ai⊂A,ai≠a'[1]。
但对于模拟量,由于是整个实数域,没有固定的值,所以最大似然译码应借鉴极限的概念,对于输入的信号S,S⊂R,根据一定的编码规则f,得到冗余的信息T,T⊂R,其中,T=f(S),其码字为{S,T},通过一定的无线信道后,得到的信息为{RS,RT},则模拟量的最大似然译码即为选择一个最接近原信号的S',使Pr{RS,RT|S}最大,应用极值的求解方法即可得到近似解S'。
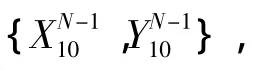

由于是四位循环编码,为了使错误概率进一步降低,可以得到
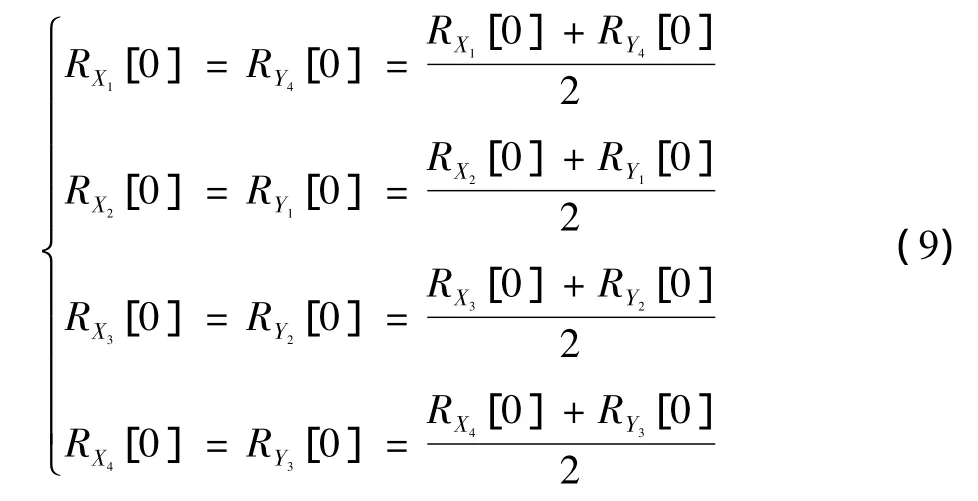


由于 Baker’s map 的每一次变换都是线性的[13],所以可以得到
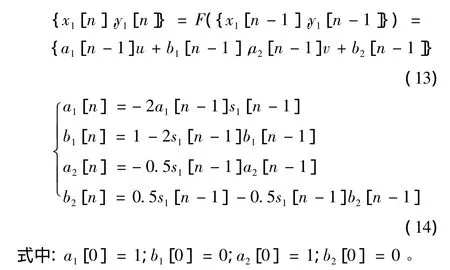


4 仿真及结果分析
本文提出的模拟编码主要是用来传输模拟信号,也可以用来传输数字信号,为了与数字编码相比较,本文将用模拟编码传输JPEG图像信息,通过镜像Baker码和四位循环Baker码相比较,得出结论。
本文对255×256的Lena图像进行处理,对于Lena图像,其每个像素点是用8位二进制表示的0~255的数,传统的数字编码是将每个像素点扩展成二进制表示,对255×256×8的二进制的码流进行处理。而本文提出的模拟编码则是将像素点看作一个个实数来处理。
1)把JPEG图像的每个像素点通过(x-128)/128变换成[-1,1]之间的小数,进行四位Baker码编码。
2)将编码后的信息通过加性高斯信道,通过控制信噪比(SNR)来比较图像的失真度。
3)将加噪后的信息进行最大似然译码,把[-1,1]之间的小数经(x×128)+128变换成0~255之间的像素点,并还原出图像,便于对比。
通过分别对255×256的Lena图像进行镜像Baker码和四位循环Baker码进行处理,由图4~图7可以明显看出,经四位循环Baker码编码处理的图像,其噪声点明显减少,抗噪声性能更强,纠错能力得到明显加强。

图5 13 dB噪声下图像比较
在信噪比为7 dB和13 dB时,由四位循环Baker码恢复的图像的噪声点明显比镜像Baker码少,图像质量得到一定的改善;在信噪比为19 dB和25 dB时,由四位循环Baker码恢复的图像与源图像有略微的差别,比镜像Baker码的纠错性能有一定的提高。

图6 19 dB噪声下图像比较

图7 25 dB噪声下图像比较
4)峰值信噪比PSNR,是一种评价图像的客观标准,通过PSNR值来衡量图像的品质,即

式中:x代表原始灰度图像的灰度值;y代表处理后图像的灰度值。
5)对Lena图像,通过四位循环Baker编码,根据得到的数据,得出SNR-PSNR曲线,并与镜像Baker码的性能相比较,如图8所示。

图8 镜像Baker码与四位循环Baker码性能比较
由图8可看出,在信噪比低于10 dB的信道环境中,镜像Baker码和四位循环Baker码的PSNR随着SNR呈近似线性的增长,改进的编码方法的纠错性能略好。在信噪比高于10 dB的信道环境中,在四位循环Baker码的纠错能力与镜像Baker码相比有较大的提高。
特别地,对于图像来说,PSNR在30 dB以上才算是好图像,由图8可以看出,四位循环Baker码在信噪比16 dB即可使PSNR达到30 dB,而镜像Baker码则需要信噪比达到20 dB以上,由此可看出:改进的编码算法纠错性能有一定的提高。
5 结束语
本文基于混沌基本理论和编码理论,通过对Kai Xie和Jing Li(Tiffany)提出的镜像Baker码的编码方法进行改进,利用循环结构,增加码元之间的相关性,构造出一种简便、失真小、性能好的四位循环Baker码。并根据最大似然译码算法,将其应用于数字图像的传输上。经MATLAB仿真,与镜像Baker码性能相比较,可以看出:在低信噪比(SNR<10 dB)环境中,四位循环Baker码的纠错能力比镜像Baker码略好;在高信噪比(SNR>10 dB)环境中,其有效作用环境更加宽。尤其在高信噪比情况下,四位循环Baker码的纠错能力比镜像Baker码有很大的提升。特别对于数字图像传输来说,通过四位循环编码,可以大大提升图像的质量,在低信噪比情况下,仍能得到质量较好的图像,弥补数字纠错编码低信噪比的缺陷。
进一步的研究有三个方面:首先,进一步对Baker码进行研究,特别是其编码的结构,找到一种更好的纠错性能更好的编码方法;其次,通过对混沌理论的进一步研究,找到一种距离扩散更快的混沌模型,提高模拟量编码的纠错能力;最后,对模拟量信源的压缩感知进行研究,搭建出一种基于压缩感知和模拟量编码的通信系统。
:
[1]傅祖芸.信息论[M].西安:电子工业出版社,2007:240-244.
[2]贺鹤云.LDPC码基础与应用[M].北京:人民邮电出版社,2009:104-107.
[3]樊昌信,曹丽娜.通信原理[M].北京:国防工业出版社,2010:25-53.
[4]LIU Yang,LI Jing,XIE Kai.Efficient image transmission through analog error correction[C]//Proc.IEEE Workshop on Multimedia Signal Processing(MMSP).Hangzhou:IEEE Press,2011:1-6.
[5]郭凯.H.264中SP帧抗误码应用研究[D].北京:北京邮电大学,2009.
[6]THOMAS G,MARSHALL J.Coding of real-number sequences for error correction:A digital signal processing problem[J].IEEE Journal on Selected Areas in Communications,1984,SAC-2(2):381-391.
[7]WOLF J K.Analog codes[C]//Proc.IEEE International Conference on Communications.Boston,MA,USA:IEEE Press,1983:310-312.
[8]LIU Yang,LI Jing,XIE Kai,et al.Wireless data sensing and transmission through analog codes[C]//Proc.46th Annual Conference on Information Sciences and Systems(CISS).Princeton,NJ:IEEE Press,2012:1-6.
[9]XIE Kai,LI Jing.Chaotic analog error correction codes:the mirrored Baker’s codes[C]//Proc.IEEE Global Teleommunications Conference.Ottawa,Canada:IEEE Press,2010:1-5.
[10]CHEN B,WORNELL G W.Analog error-correcting codes based on chaotic dynamical systems[J].IEEE Trans.Communications,1998,46(7):881-890.
[11]XIE K,TAN P Y,CHONG N B,et al.Analog turbo codes:a chaotic construction[C]//Proc.IEEE International Symposium on Information Theory.Seoul,Korea:IEEE Press,2009:894-898.
[12]冯久超.混沌信号与信息处理[M].北京:清华大学出版社,2012:3-7.
[13]PAPADOPOULOS H C,WORNELL G W.Maximum likelihood estimation of a class of chaotic signals[J].IEEE Trans.Information Theory,1995,41(1):312-317.
