一种基于C均值的模糊核聚类图像分割算法

彭建喜

(佛山职业技术学院，广东佛山 528000)

图像分割是把图像分解成具有特殊含义的不相交的空间区域，然后分离出有价值目标的技术和过程，是成功进行图像分析、模式识别与理解和图像编码的关键技术之一，图像分割的质量直接到影响后面进行的分析、识别和解释的质量［1-2］。近年来，随着人们对图像分割进行深入的研究，提出了各种图像分割方法，包括直方图阈值的方法、最大熵值方法、区域分割增长的方法和微粒群优化的分割方法等，其中Bezdek提出的模糊聚类算法FCM，是一种基于目标函数的非线性迭代最优化方法，通过引入像素聚类样本到聚类中心的隶属度来表示像素样本的隶属度，该类隶属度的大小能够客观反映出算法中样本点隶属于某一类的程度［3］。但FCM算法对初值敏感，很大程度上依赖初始聚类中心的选择，并且容易收敛于局部极小值，用于图像分割时，隶属度的计算只考虑了图像中当前的像素探值，而未考虑邻域像素点的空间信息，故对分割含有噪声图像不理想。为了有效解决FCM图像分割方法所存在的问题，Yang和Chuang等人从不同角度考虑了像素点的空间信息，Gomez提出了一种自适应的空间聚类算法，该算法提出在模糊C均值聚类算法的目标函数中加入像素点空间信息，提高算法的鲁棒性，但对于对低灰度信息的图像分割，该算法就会失效。刘刚等采用轮廓波变换在变换域对图像做降噪预处理，但容易在处理结果中产生伪吉布斯效应，Chuang为解决低灰度信息问题，通过在目标函数中加入径向基函数来区分像素点之间的相似度［4-10］。针对以前方法的进行研究与分析，本文对FCM分割算法的改进主要在两个方面:首先，建立一种新的称为近似模糊C均值聚类算法，通过数据约简大幅度降低数据个数，节省计算时间;然后在FCM算法中利用核函数将约简后的数据映射到非线性高维空间中进行聚类划分，最后使用像素点的空间邻域信息修正当前像素空间的隶属度值，得到更加准确的聚类结果。

1 经典的模糊C均值聚类分割算法

由Bezdek提出的模糊C均值聚类算法，其实质是根据图像分解后像素样本与每个聚类中心的加权相似性测度，通过对目标函数进行非线性迭代优化方法，然后确定最优聚类，它给出每个样本隶属于某个聚类的隶属度，即使对于很难明显分类的变量，FCM也能得到较为满意的效果。FCM通过将图像I={f(x，y)，0≤x＜m，0≤y＜n}分成C类来实现图像的分割，其中f(x，y)为特征数据，Qk(x，y)是f(x，y)对于第k类的隶属度，为了计算各个样本点相对于聚类中心的隶属度，聚类目标函数可定义为

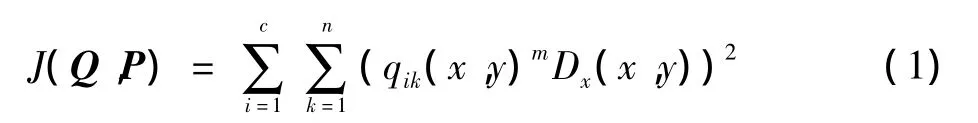
式中:Q=［qik(x，u)］为模糊分类矩阵;P=［p1，p2，…，pc］为聚类中心集合;m∈［1，∞)是控制聚类结果的权指数，一般赋值为2;Dx(x，y)为f(x，y)到聚类中心pk的距离，表示为

图像FCM分割就是通过多次迭代确定隶属度函数和聚类中心，使目标函数获得最小值。利用拉格朗日乘数法来求解使得J(Q，P)达到最小值的满足下列等式

Bezdek利用梯度下降方法，通过对模糊分类矩阵Q与聚类中心矩阵V不断进行迭代算法，以修正聚类中心值以及各样本的隶属度，最终寻找出样本数据所含有的分类特性，使各样本划分到其隶属度最大的一类中。该算法对初始聚类中心或隶属度矩阵有较为敏感，参数初值选取决定着聚类结果的优劣和稳定性;当初始聚类中心偏离全局最佳聚类中心比较大时，FCM很有可能陷入局部最小值。

2 近似模糊C均值聚类的中心初始化

2.1 数据约简

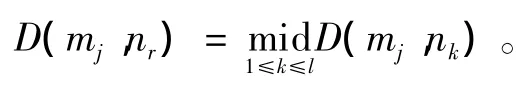
3)如果D(mj，nr)＞γ，l=l+1，nl=mj;否则，令nr=nr∪mj，j=j+1 。

4)如果j＜i，则转到步骤2);否则，将nk更新为其自身数据集合的平均值。

2.2 加入特征空间中的模糊核聚类算法

在线性空间中难以划分的问题利用核映射处理来处理，将数据从线性空间映射到高维的非线性空间解决。

先通过一个非线性映射Φ:X→F(X∈Rp→Φ(x)∈Rq，q＞p)将输入空间X变换至高维特征空间F;然后在特征空间F中进行聚类。

对在FCM目标函数中使用核映射，则得到目标函数息，得到与模糊C均值接近的聚类中心。

设原始数据集合M中含有i个不同的样本M={m1，m2，…，mn}⊂Rs。分析聚类问题就是将 {m1，m2，…，mi}区分为M中的c(2≤c＜i)个子集，相似的样本应要求尽量在同一子集(聚类)内，c为聚类数目。约简后数据集合为N={n1，n2，…，ni}⊂Rs。D(m，S)表示数据m与数据集合S间的距离。则数据约简算法的步骤如下:

1)初始化阈值，其中 γ，l=1，nl=m1，j=2 。

2)对聚类样本数据mj，计算整数值r，使其满足

其中

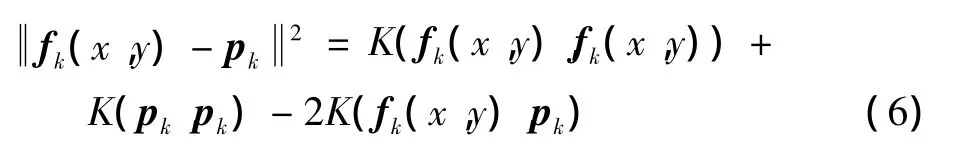
由核代入技巧知，上述内积定义了F中的一个核函数K(x，y)，满足K(x，y)=(fk(x，y)－pk)T(fk(x，y)－pk)。Dx(x，y)为特征空间中的欧氏距离，由于核的代入，在原输入空间中诱导出了一类核依赖的新的距离度量，由此将FCM在欧氏距离下的执行推广到了同一空间中不同距离度量的新的聚类。

本文将式(6)中高斯核函数代入式(5)中，得到目标函数为

使用拉格朗日数乘法，首先对qk(x，y)m求偏导数，得到隶属度迭代式

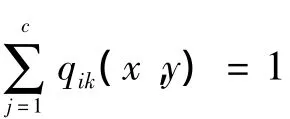
求出λ代入式(9)

利用高斯核函数，代入高斯核函数，则目标函数变为

可以解得聚类中心迭代表达式

2.3 加入空间约束信息

对图像进行非线性高维聚类划分后，通过表征空间邻域像素对初始聚类中心作用的先验概率来修正各像素样本的聚类划分，形成最终修正的分割效果。利用Chuang Keh-Shih的研究成果，对已完成高维非线性空间核聚类划分后并进行数据约简的图像进行空间邻域隶属度约束处理。划分后的邻域信息为

式中:NB(fj(x，y))表示像素fj(x，y)的领域大小;qim(x，y)表示像素fm(x，y)属于i类的隶属度值。Hik的值是除了当前空间像素领域区域内其他像素属于i类的隶属度和。经过邻域隶属度约束修正后的隶属度的迭代表达式为

式中:p，q是正则化参数，用于控制最终隶属度值的控制参数。式(14)表示邻域空间中某一类的像素和其空间邻域中像素同属于一个类时Hik的值就越大，对原始隶属度的修正就越大，反之则像素隶属度值就减小。最终本文的分割算法过程步骤如下:

1)选择聚类有效性指标计算方法，设置模糊系数m，设定聚类个数的最小值cmin、最大值cmax。

2)采用本文2.1节的方法得到约简后的数据集合Nc={n1，n2，…nic}⊂Rs。

3)采用核估计方法实现聚类中心的估计，确定初始聚类中心。

4)再根据式(12)与式(10)分别计算或更新初始聚类中心和划分矩阵。

5)利用式(14)修正隶属度原型模式。

6)判断迭代次数达到事先设定的最大次数，达到迭代次数则停止，否则继续迭代。

3 实验结果分析

为验证本文所提算法的有效性，对正常大脑磁共振图像进行实验。初始参数设置:矩阵指数m=2，单步最小变化为0.000 5，最大迭代次数为100，聚类类别数为8，核参数均为150。参与比较的算法为原始的模糊C均值聚类算法、PSOFCM算法、KFCM算法、DWKFCM和本文算法，所有算法收敛精度相同且为ε，其他参数按原有文献设定，运行20次取平均值。

为了验证几种分割算法的量化比较，采用合成图像的分割精度和运行时间均值作为分割评价指标，定义合成图像的分割精度为

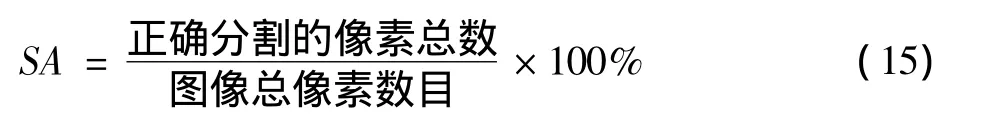
图1为FCM算法、PSO_FCM算法、KFCM算法、DWKFCM算法及本文算法分割后图像与本文算法的比较结果。

图1 大脑磁共振图像分割结果对比图

图1a为是一幅181×181像素的大脑磁共振图像，图1b为原始FCM算法，图像分割效果有些模糊，一些细节还没有分割出来，图1c分割效果对比FCM算法稍好，但在中间部位的信息有一定的丢失。可以看出，本算法分割效果不错，不但误分割很少，且分割的脑灰质和脑白质边缘也很光滑，在传统模糊核聚类算法与动态加权模糊核聚类算法的分割结果里，都有较多的脑白质被误分为脑灰质和脑脊液，同时分割的目标边缘也毛糙;减小了过度分割的现象，又保留了图像的细节部分，图像中的主要目标较为准确、清晰地分割出来。

图2是FCM、KFCM、DWKFCM和本文算法四种算法对图1a进行分割时的算法收敛次数对比图。从图2可以看出，本文算法收敛次数很少，在很短时间内就能找到目标函数的最小值，具有明显的速度优势。

图2 几种算法的目标函数收敛对比图

表1为FCM、PSOFCM、KFCM、DWKFCM和本文算法的性能比较结果。

表1 几种算法性能比较表

从表1可以看出，在同一迭代次数处，本文算法从图像分割精度和运行时间上都大大高于其他几种算法，实验表明本算法具有较好的适应性和鲁棒性。

4 结束语

针对传统模糊核聚类算法存在的问题，本文将数据约简技术与模糊核聚类算法相结合提出一种新的算法，先通过数据约简大幅度降低数据个数，节省计算时间;然后在FCM算法中利用核函数将约简后的数据映射到非线性高维空间中进行聚类划分;最后使用像素点的空间邻域信息修正当前像素空间的隶属度值，得到更加准确的聚类结果。改进的受空间约束的模糊核聚类算法简单且运算速度更快，再结合空间邻域信息修正当前像素的隶属度值，得到更加准确的聚类结果。实验结果表明，该算法具有较好的分割图像质量，相比其他几种图像算法有更快的分割速度及更准确的分割精度，表现出了较强的鲁棒性和较好的工程价值。

:

［1］刘刚，梁晓庚，张京国.基于轮廓波变换和改时模糊C均值聚类的红外图像分割［J］.系统工程与电子技术，2011，23(2):443-448.

［2］曲福恒.一类模糊聚类算法研究及其应用［D］.长春:吉林大学，2009.

［3］CHUANG K，TZENG H，CHEN S，et al。Fuzzy C mean clustering with spatial information for image segmentation［J］.Elsevier Science，2006(30):9-15.

［4］杨润玲，周军妮，刘利.基于改进型FCM聚类的图像分割新方法［J］.电视技术，2008，32(6):12-14.

［5］丁震，胡钟山，杨静宇，等.FCM算法用于灰度图像分割的研究［J］.电子学报，1997，25(5):39-43.

［6］匡泰，朱清新，孙跃.FcM算法用于灰度图像分割的初始化方法的研究［J］.计算机应用，2006，26(4):784-786.

［7］高新波.模糊聚类算法的优化及应用研究［D］.西安:西安电子科技大学，1999.

［8］庞冬冬，史健芳.基于改进主动轮廓模型的图像分割算法［J］.电视技术，2013，37(1):41-44.

［9］WANG S.A new integrated clustering algorithm GFC and switching regressions［J］.Int.J.Pattern Recognition and Artificial Intelligence，2002，16(4):433-447.

［10］GOKCAY E，PRINCIPE J.Information theoretic clustering［J］.IEEE Trans.PAMI，2002，24(2):158-171.