基于DCT的自适应多重彩色图像盲水印算法

谢 斌，刘 珊，任克强

(江西理工大学信息工程学院，江西赣州 341000)

数字水印技术发展至今，已被公认为是版权保护和隐蔽通信的重要手段之一［1］。随着多媒体技术的广泛应用，设计较为成熟的数字图像水印方案是现阶段必须解决的重点问题之一［2］。然而，理论分析和实验结果表明，现有的图像水印算法存在的问题主要表现在以下几个方面［3］:1)未能有效结合载体的具体特征，使算法的稳健性不够理想;2)用伪随机序列作为水印，其信息量较小且版权意义不够直观;3)绝大多数算法都是单水印系统，其在不同阶段的版权认证及多著作权标识等方面很难满足人们的需要;4)提取水印时需要用到原始载体图像，不能实现盲提取，其实用性较弱;5)一些算法的水印载体为灰度图像，其适用性不够;6)在选择水印嵌入位置时，未能较好地考虑人类视觉特性，容易造成载体图像的重要特性产生可感觉到的失真，从而影响了算法的稳健性。

针对以上问题，文中利用离散余弦变换理论，结合人类视觉系统特性，提出了一种能够抵抗多种常规攻击的自适应多重彩色图像盲水印算法，以二值图像作为水印，以彩色图像作为载体，将不同的水印数据分别嵌入到离散余弦变换后的低频和中频系数，并进行了多重水印的嵌入、提取及抗攻击实验。实验结果表明，文中所提多重图像水印算法对马赛克、高斯、椒盐及压缩等攻击均具有较强的稳健性。

1 离散余弦变换

离散余弦变换与图像压缩标准兼容，具有很好的能量集中特性，它可以将原始图像信息块转换成代表不同频率分量的系数集［4］。图像信号经过离散余弦变换后，其能量主要集中在低频部分，不重要分量的描述只需要很少的比特数。当信号具有接近马尔科夫过程的统计特性时，离散余弦变换的去相关性接近K-L变换，具有良好的去相关性能［5］。因此，在图像信号处理方面离散余弦变换得到了广泛的应用。在彩色图像处理过程中通常采用二维离散余弦变换。

设彩色载体图像f(x，y)为M×N大小的矩阵，则其二维离散余弦变换(DCT)为

二维离散余弦变换逆变换(IDCT)为

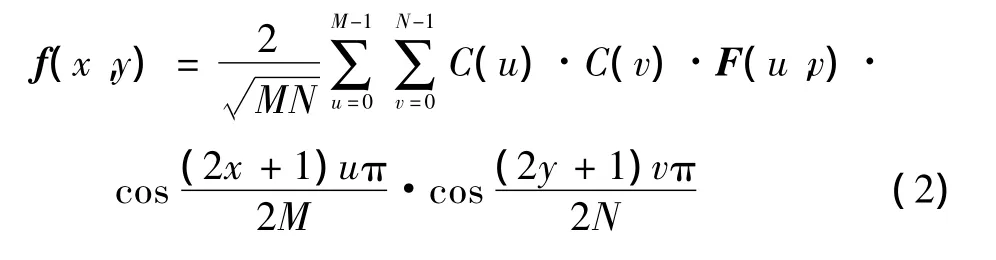
2 水印的置乱

水印的置乱是利用某种算法在保持像素总数不变的情况下将水印图像各个像素的位置打乱以消除它们之间的相关性。水印图像经过置乱后，能够使可能受到的局部影响分散到整幅图像中，一定程度上提高了算法的稳健性和安全性。图像置乱的方法主要有Arnold变换、幻方变换、Hilbert曲线变换和Fibonacci变换等。其中Arnold变换简单易行，且置乱效果相对较好［3］。

对于N×N大小的图像矩阵F(x，y)，设像素坐标x，y∈ {0，1，2，…，N-1}，则其 Arnold 变换为

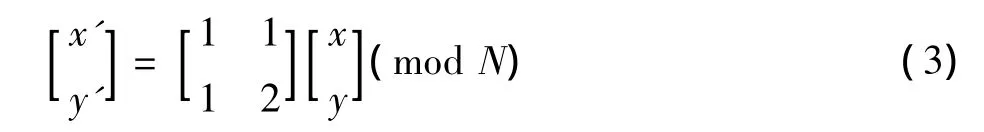
迭代地对数字图像使用Arnold变换则可得到一系列不同置乱结果的图像。文中选择Arnold变换对N×N大小的水印A和水印B分别进行置乱，得到置乱后的二值水印。图1a、图1b为待嵌入的水印A和水印B图像，图1c、图1d是置乱后的水印A和水印B图像。

图1 原始二值图像水印及置乱后的水印

3 水印图像的嵌入算法原理

载体图像经过离散余弦变换以后，其系数矩阵的能量从左上角至右下角迅速递减，依次为直流分量、低频分量、中频分量和高频分量［4］。其中直流分量和低频分量的能量最大，主要描述图像的轮廓。高频分量主要描述图像的细节部分，能量最小，因此其嵌入容量相对较小，对它的改变将会较明显地影响水印的透明性，且容易受到各种信号处理的破坏［5］。另外，彩色载体图像通常可以分解成红、绿、蓝三基色，其中红色分量和蓝色分量对常规JPEG压缩的抵抗能力较弱，而绿色分量经过JPEG压缩后能量损失相对较小［6］。文中选择将不同的水印数据嵌入在彩色载体图像绿色分量的低频和中频离散余弦系数中，以此提高算法的稳健性。水印嵌入算法步骤如下:

1)为了提高了算法的稳健性和安全性，利用Arnold变换对水印A和水印B进行置乱预处理，得到置乱后的水印数据。

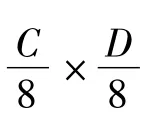
3)考虑到人眼视觉系统特性及图像画面的景深因素，图像画面的边角位置通常是人们最容易忽视的部分。所以文中选择在彩色载体图像4个边角部分的N×N个8×8离散余弦变换子块的低频分量和中频分量分别嵌入水印A的数据和水印B的数据。水印A的数据和水印B的数据在8×8离散余弦变换子块中的嵌入位置如图2所示，通过修改低频系数d的取值Wd和修改中频系数z的取值Wz来实现。系数修改算法如图3所示，嵌入水印A数据后的系数D其取值WD由周围的4近邻离散余弦变换系数值X1～X4共同决定，嵌入水印B数据后的系数Z，其取值WZ由周围的4近邻离散余弦变换系数值X3～X6共同决定。

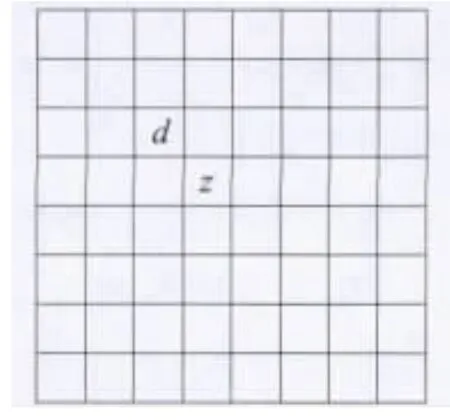
图2 水印嵌入位置

图3 低频、中频系数修改方案

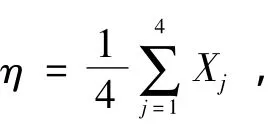
式中:η为低频系数d周围的4近邻系数值A1～A4的平均值;ζ为中频频系数z周围的4近邻系数值A3～A6的平均值;μ为嵌入系数，水印的嵌入深度μη和μζ可以根据载体图像内容及特性的不同实现自适应调节，因而可以较好地利用人眼视觉掩蔽特性，提高水印的不可知性。

4)按照上述方法，依次将水印A和水印B的数据嵌入到彩色载体图像后，对所有的8×8离散余弦变换子块进行分块离散余弦逆变换，得到含两个水印的载体图像绿色分量，然后将其与原先未变化的载体图像红色分量R及蓝色分量B进行重构得到含水印A和水印B的彩色图像。

4 水印图像的提取算法原理

水印提取算法步骤如下:

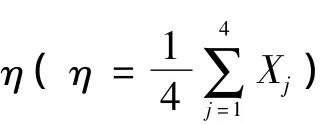
4)按照以上方法，对所有含水印A、水印B数据的绿色分量8×8离散余弦变换子块进行水印数据的提取，分别得到N×N个置乱后的水印A数据和N×N个置乱后的水印B数据。

5)对上述方法得到的置乱后的水印A数据和置乱后的水印B数据进行Arnold逆置乱，得到提取出的水印A图像和提取出的水印B图像。

5 实验数据及分析

文中选择大小为1 280×800的彩色图像作为水印载体，如图4所示。水印A和水印B均采用64×64的二值图像。

图4 原始载体图像

二重水印数据的提取是其嵌入的逆过程。由于嵌入的两个水印位置已经确定，因此在水印提取时不需要用到原始彩色载体图像，即文中算法可以实现盲提取。图5为正常嵌入水印A和水印B后的彩色图像，其各方面性能与原始彩色载体图像保持高度一致，肉眼很难察觉二者的区别，说明文中算法具有较好的不可感知性。图6a为正常提取的水印A，它与原始水印的相似度NC=0.993 4，图6b为正常提取的水印B，它与原始水印的相似度NC=0.993 2，由此可以看出文中水印的盲提取算法效果较好。

图5 含水印A和水印B的彩色图像

图6 正常提取的水印

通过对含有二重水印的彩色图像进行不同类型的攻击实验，将从中提取的水印与原始水印进行相似度比较来检测算法的抗攻击能力。文中对含水印A和水印B的彩色图像进行了马赛克、高斯、椒盐及压缩等攻击测试，实验数据如表1所示。

根据表1所示实验结果可知，经过不同强度的马赛克、高斯、椒盐及压缩攻击后，提取出的水印A、水印B与原水印A、水印B的相似度较高，即便在较大强度攻击下提取出来的水印仍然比较清晰。以上实验结果表明，文中所提算法对上述各类攻击具有较好的稳健性。

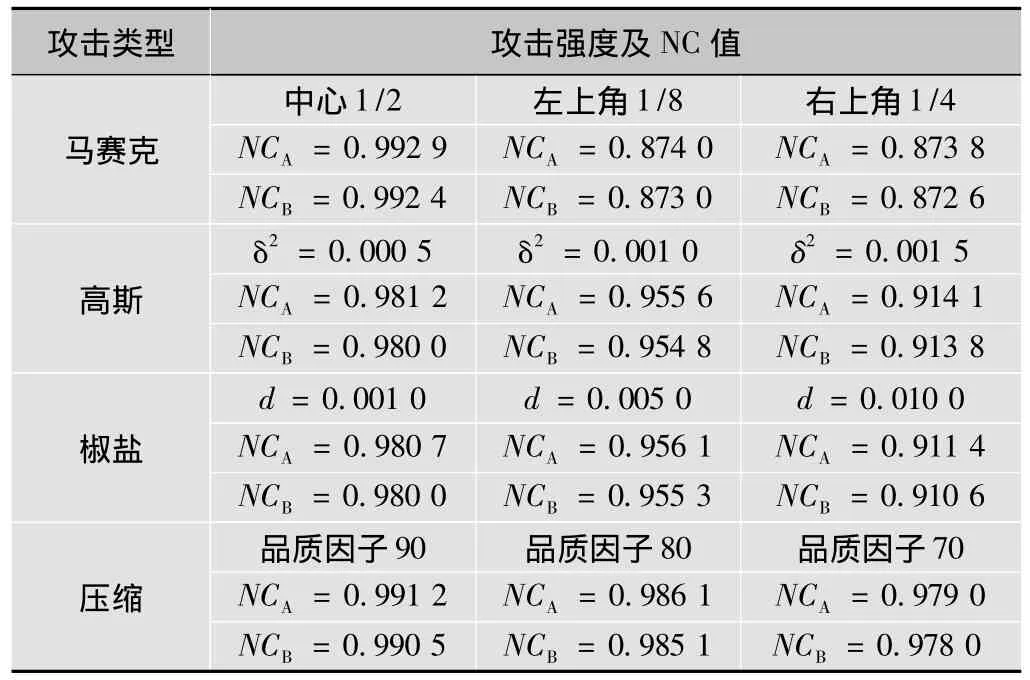
表1 攻击后水印A及水印B的相似度

6 总结

文中针对现有图像水印算法的一些不足，结合人眼视觉特性，提出了一种基于离散余弦变换的自适应多重彩色图像盲水印算法，将不同的水印分别嵌入到彩色载体图像绿色分量的离散余弦变换低频系数和中频系数，较好地实现了不同水印在彩色载体图像中的嵌入及盲提取。实验结果表明，该算法较好地平衡了水印系统的透明性与稳健性之间的关系，对常规攻击具有较强的抵抗能力。其在不同阶段的版权认证及多著作权标识等方面具有一定的应用价值。由于针对图像的攻击种类繁多，如何进一步提高算法对其他攻击尤其是几何攻击的稳健性是今后研究的重点。

:

［1］LI Lizhong，GU Qiaolun，GAO Tiegang.A zero-watermarking algorithm based on fuzzy adaptive resonance theory［C］//Proc.FSKD'09.Tianjin:IEEE Press，2009:378-382.

［2］王海峰，吴冬燕，吴卫华.基于矩阵范数分析的自适应数字水印算法［J］.电视技术，2012，36(19):51-54.

［3］ARYA M，SIDDAVATAM R.A novel biometric watermarking approach using LWT-SVD［J］.Communications in Computer and Information Science，2011(147):123-131.

［4］姚军财.基于离散余弦变换的图像半盲水印技术研究［J］.电视技术，2012，36(17):37-39.

［5］ZHANG Y，WU J，SHU H.Robust watermarking using conjugate symmetric sequency ordered complex hadamard transform and normalization［C］//Proc.2010 3rd International Congress on Image and Signal Processing(CISP).Yantai，China:IEEE Press，2010:1176-1180.

［6］YAO Juncai.Measurements of human vision contrast sensitivity to opposite colors using a cathode ray tube display［J］.Chinese Science Bulletin，2011，56(23):2425-2432.