一种基于MQ编码器的图像联合压缩加密算法

2014-09-18谢凯明邓家先

电视技术 2014年9期

谢凯明，邓家先

(海南大学信息科学技术学院，海南海口 570228)

为减小数字图像存储空间、降低传输带宽、提高信息的安全性，数字图像压缩和加密技术成为当前研究的一个热点领域［1-11］。同时为提高数据传输的实时性，将SPIHT、EZW等压缩算法与加密技术相结合成为一个新的研究方向［12-14］。文献［12］提出先对小波系数使用标准映射和logistic映射进行扩散和混淆来加密，再利用SPIHT算法进行压缩，但是加密改变了图像的能量分布和小波系数间的相关性，降低了图像的压缩效率。文献［13］提出在EZW编码的基础上引入自适应算术编码来实现联合压缩加密，但是该算法使用的是固定密钥，密钥空间小、周期短、敏感性低，不能很好地抵抗攻击。文献［14］利用EZW编码的渐进式传输特性和树形结构特征进行加密，取得了较好的压缩加密效果，但是该算法将密文反馈到密钥发生器，使得混沌映射的高精度迭代次数太多导致加密时间太长，降低了整个系统的运行效率。

针对文献［12-14］存在的问题，本文提出的算法利用MQ算术编码器对数据快速自适应概率估计的特性，使用其对EZW编码进行改进，结合chebyshev映射对初值、参数的高敏感性和线性反馈移位寄存器(Linear Feedback Shift Register，LFSR)的简单易实现来产生混合混沌序列，并将其作为流密钥对比特平面编码产生的上下文和判决进行修正。加密过程约束在比特平面编码和熵编码之间进行，并不破坏小波变换后各分辨率子带系数间的相关性。仿真结果表明，该算法不仅具有很好的安全性能和压缩效率，而且具有较高的时间效率。

1 MQ编码器简述与加密可行性分析

MQ编码器是一种基于上下文CX(Context)的自适应二进制算术编码器，其自适应的概率估计模型能够使输出的码长逼近信源的熵，已经广泛应用于JPEG2000、H.264等图像和视频压缩编码算法［15-16］。CX用于选择编码判决D(Decision)时所用的概率估计值，可以很好地降低信源的相关性。利用条件交换和概率估计状态机中的贝叶斯学习过程实现符号概率模型自适应过程，并采用位填充技术解决编码中的进位问题，是一种高效率物理可实现的压缩编码算法。其算法如图1所示，CODE0与CODE1编码过程类似，未予列出。

图1 MQ编码算法流程图

由图1知，根据判决D的不同分别进行CODE0或者CODE1编码过程。I(CX)用于索引Qe值，根据概率估计结果的不同对D进行大概率符号编码(CODEMPS)或者小概率符号编码(CODELPS)。因此，可以使用密钥对D进行修正来改变原来的CODE0或者CODE1编码过程，进而改变原来的CODEMPS或者CODELPS编码过程;同时，也可以使用密钥对CX进行修正，并通过I(CX)索引获得新的Qe值来改变原来的概率空间，从而使得最后调用byteout()函数输出的码流发生变化来实现算术加密。

2 改进零树编码

零树编码是由Shapiro提出的一种基于小波变换和比特平面编码的方法［17］，利用了小波变换后各级子带系数在空间上和方向上所呈现出的带间相似性进行数据压缩，本文引入MQ算术编码器对其进行改进，改进零树编码的框图如图2所示。

图2 改进零树编码

由于MQ编码器有CX和D两个输入参数，现对比特平面编码产生的判决使用相邻系数或者相邻集合的重要性进行分类，称之为系数上下文或集合上下文。与优化截断的嵌入式分块编码(Embedded Block Coding with Optimized Truncation，EBCOT)［18-20］算法一样，系数上下文进一步细化为零编码上下文、幅值细化上下文、符号编码上下文，其具体计算方法与EBCOT中的一致，这里不再赘述。下面阐述集合上下文的形成过程。以三级小波变换为例，零树结构如图3所示。本文对具有相同分辨率的相邻集合重要性进行分类来形成集合上下文CXS，集合的邻居关系如图4所示，将8个邻居形成的256种上下文合并成4种集合上下文［13］，CXS表示为

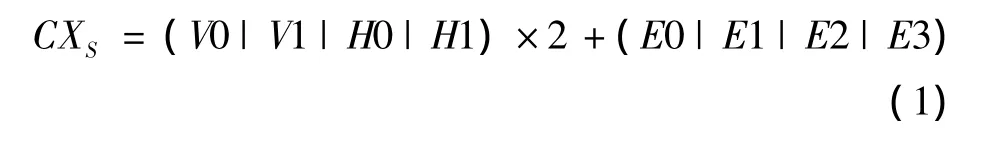
其中:“|”表示逻辑或运算，V0，V1，H0，H1，E0，E1，E2，E3表示X的邻居，其取值为{0，1}(其中0表示不重要，1表示重要)。

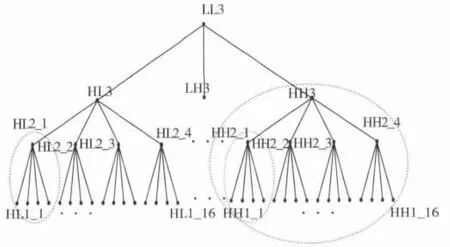
图3 零树结构

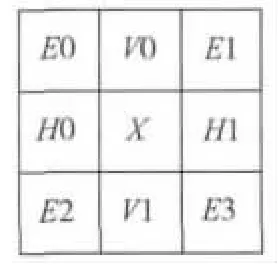
图4 集合邻居

3 图像联合压缩加密

3.1 密钥的产生

本文采用chebyshev混沌映射迭代运算来产生混沌序列，并将其与基于LFSR产生的m序列进行非线性运算来生成最终的混合混沌序列密钥，密钥生成过程如图5所示。

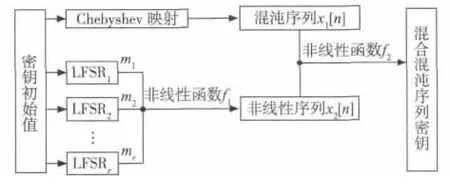
图5 混合混沌序列密钥的生成

chebyshev混沌映射的迭代方程为

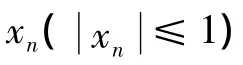
设ni级LFSR产生的m序列的周期为Ti，则非线性序列x2［n］的周期为

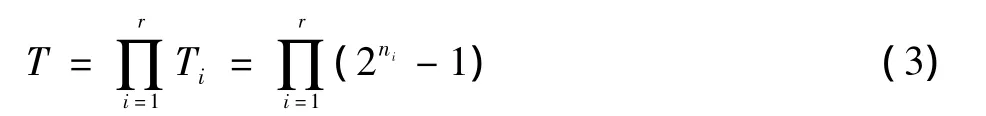
其中r表示m序列的组数。显然，经非线性函数运算后，密钥序列的复杂度会得到很大的提高。

3.2 压缩加密算法的实现

本文提出算法的原理如图6所示。

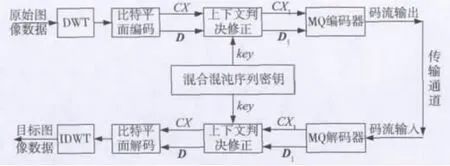
图6 图像联合压缩加密算法原理框图

使用MQ编码器对EZW算法进行改进，直接对离散小波变换后零树的集合重要性和系数重要性进行编码，将混合混沌序列作为流密钥对比特平面编码产生的数据对(CX，D)进行修正，并将修正后的(CX1，D1)送入MQ编码器进行熵编码，从而实现联合压缩加密。因为(CX1，D1)改变了MQ编码时的概率空间，所以MQ编码器不仅提高了数据的压缩效率，而且在数据压缩的同时实现了算术加密。解密解压缩的过程与之相反，不予赘述。下面分别阐述判决修正和上下文修正的加密原理。

1)基于判决修正的算术加密原理如下:

设D=(d1，d2，…，dN)表示比特平面编码产生的长度为N的二进制判决矢量，定义一种运算

其中key表示图5所产生的混合混沌序列密钥，D1=(d11，d12，…，d1N)也是长度为N的矢量，且每个元素仍然是二进制的。即利用流密钥对判决进行某种修正来改变原来的判决，进而改变MQ编码时的概率分布，从而实现算术加密。

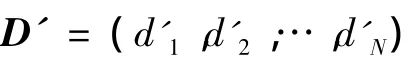
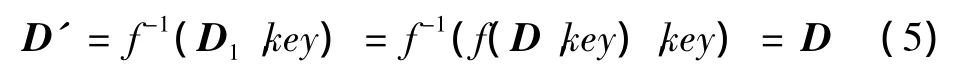
其中f-1为式(4)对应的逆运算，即要求式(4)定义的运算对正确密钥是可逆的。本文采用异或运算对判决进行修正，每使用一次流密钥进行加密后将其移位一次，以供下一次判决修正使用。

2)基于上下文修正的算术加密原理如下:

设原始上下文CX对应的取值范围为(m，m+1，…，m+L)，经密钥修正后的上下文CX1对应的取值范围为(m，m+1，…，m+L')，其中m为该类上下文的初始值，L，L'分别表示原始上下文CX和修正上下文CX1的种类。上下文修正可以表示为

其中，g()为某种运算，key表示图5所产生的混合混沌序列密钥，n表示该类上下文出现的顺序。使用式(6)进行上下文修正需要满足以下要求［13］:

(1)因为MQ编码器的概率跳转规律由上下文和判决共同确定，这就要求原始上下文和修正后的上下文必须在MQ编码器所使用的上下文的范围之内，否则会改变不同类别上下文的概率分布，从而导致压缩效率的降低;

(2)若在加解密过程中使用相同的流密钥代入式(6)对比特平面编解码产生的上下文进行修正，则送往MQ编、解码器的上下文就会相同，进而不会产生上下文引起的解密错误。因为加解密使用相同的运算进行修正，所以式(6)不需要是可逆的;

(3)对于给定的原始上下文CX和密钥key，对于不同的n，经式(6)修正后的上下文CX1不能总是固定值，否则不能改变MQ编码时的概率分布来实现算术加密。

为满足上下文修正提出的三条要求，本文在每次加密前先对流密钥key进行移位，再取移位后的最低若干位二进制数据dk与原始上下文CX进行运算，表示为

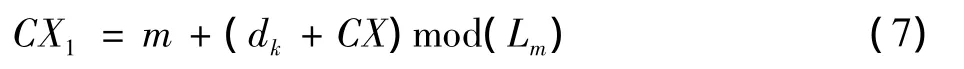
其中:mod()表示取模运算，m表示该类上下文的初始值，Lm表示修正上下文CX1的种类。

4 实验结果和数据分析

对本文提出的算法进行仿真，具体过程如下:

1)将原始图像进行三级(9，7)离散小波变换，形成3个不同分辨率的子带;

2)实验选取r=4，k=8来产生混合混沌序列。为3个不同分辨率的子带分配3组不同的密钥初始值，随机选择对应于不同分辨率级数l的LFSR和Chebyshev映射的初始值如表1。

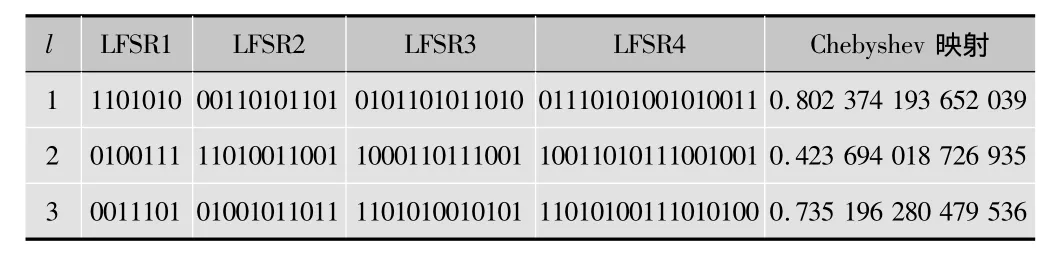
表1 密钥初始值

对应不同LFSR级数的反馈函数如下

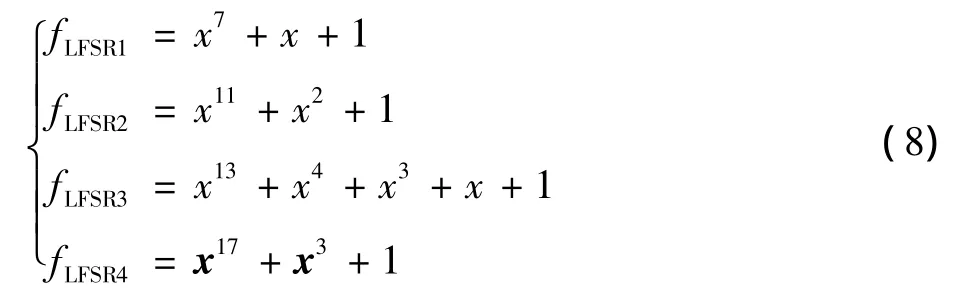
本文提出的算法中非线性函数表示为

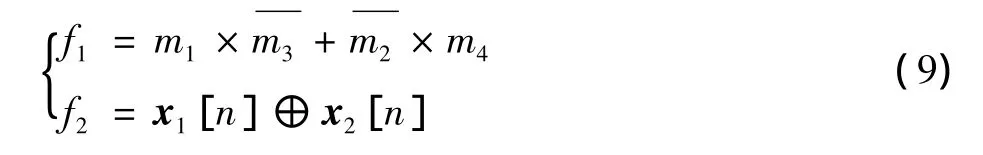
其中，“m”表示对m取反运算，“⊕”表示异或运算。

3)将生成的混合混沌序列作为流密钥对比特平面编码产生的(CX，D)数据对进行修正，并将修正后的(CX1，D1)送入MQ编码器进行熵编码，从而实现图像联合压缩加密。

4.1 重构图像的质量分析

采用大小为512×512的标准8位灰度级图像(Pepper，Barbara，Lena)对所提出的算法进行仿真，当码率分别为0.50 bpp(bit per pixel)、0.75 bpp、1.00 bpp 时，重建图像的PSNR值如表2所示。从表中可以看出，相对于原始EZW算法，在使用MQ编码器对EZW压缩算法进行改进后，重构图像的PSNR值提高了2 dB左右;在使用混合混沌序列作为流密钥对比特平面编码产生的数据对(CX，D)修正进行算术加密后，重构图像的PSNR值提高了1 dB以上。

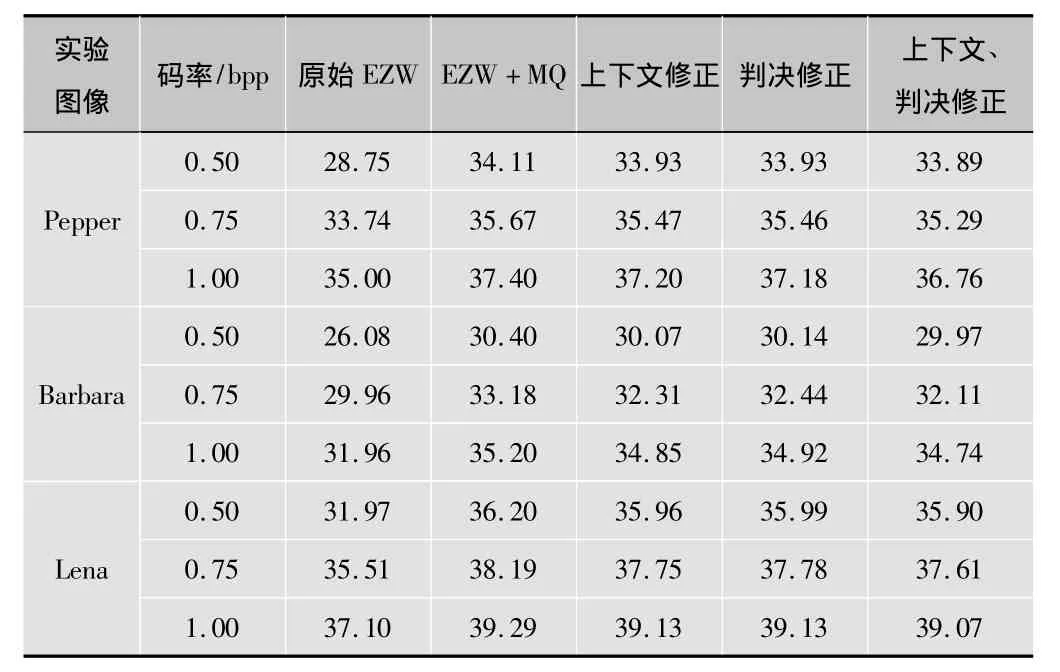
表2 原压缩算法与本文算法重构图像的PSNR比较 dB

4.2 重构图像的安全性能分析

针对文献［13］使用固定密钥不能很好抵抗攻击的缺点，本文使用混合混沌序列作为流密钥来进行加密，下面分别从密钥空间、密钥敏感性、明文敏感性、加解密速度对本文提出的算法进行分析。

1)密钥空间:因为二元域的异或相当于相加运算，结合式(3)和表1，则生成的混合混沌序列密钥的周期P为

其中S和T分别表示混沌序列x1［n］和非线性序列x2［n］的周期，h(S，T)表示求二者的最小公倍数。本文分别为3个不同分辨率的子带产生了256×128=215bit的流密钥，相应的密钥空间为23×215bit。因此，算法拥有足够长的密钥周期和密钥空间，能够很好地抵抗穷举攻击。

2)密钥敏感性测试:利用混沌现象对初值的敏感性，将Chebyshev映射密钥初始值的最后一位加1或减1来测试密钥的敏感性。仅对l=3时的Chebyshev映射秘密初始值由x3=0.735 196 280 479 536改为x3=0.735 196 280 479 537，其他的密钥初始值不变。对上下文和判决进行修正，然后逐位比较两种情况下产生的密文序列，并计算其比特变化百分比。对Pepper，Barbara，Lena测试的结果如表3所示。实验表明，在不同的码率下，位变化百分比相同且都在50%左右，说明密文对密钥是敏感的。

表3 密钥敏感性测试

3)明文敏感性测试:为测试明文敏感性，任意选取明文图像几个不同位置的像数值与1进行异或，然后使用相同的密钥对上下文和判决进行修正。随机选取Pepper，Barbara，Lena 图像的(35，78)、(69，483)、(218，256)、(379，18)、(492，508)五个位置的像数值在码率为1.00 bpp时进行测试，并将其位置顺序编号。逐位比较两种情况下产生的密文序列，计算比特变化百分比如表4所示。从表中可以看出，不同位置的微小变化，位变化百分比都在50%以上，说明明文对密钥是敏感的。

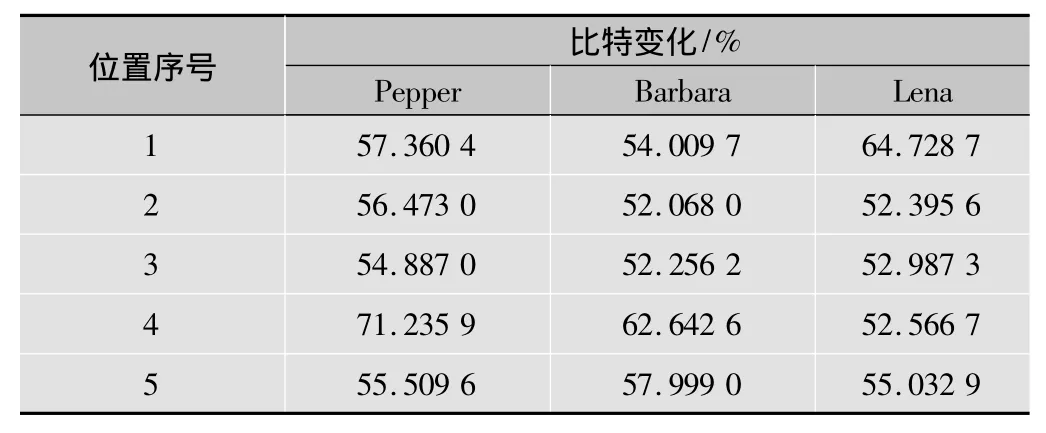
表4 明文敏感性测试

4)加解密速度:对上下文和判决修正的情况进行测试，实验结果列于表5中。从表中的数据可知，加密时间占算法总时间的百分比均小于15%，即通过增加相对短的时间进行加密来增加图像的安全性能是可行的。表中的加密时间表示加密时间占总时间的百分比。

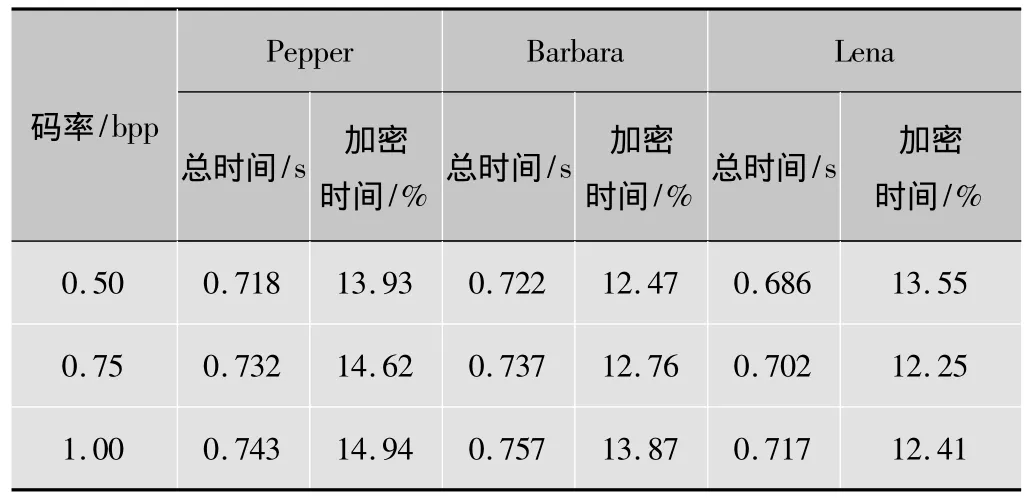
表5 加解密速度

4.3 与其他压缩加密算法的比较分析

将文献［14］提出的EZW+密文反馈压缩加密同步算法和文献［12］提出的SPIHT+SHA-1先加密后压缩的算法与本文提出的算法进行比较，采用Lena图像进行测试，结果列于表6中。结果表明，相对于前者，本文提出算法的加解密速度有了很大的提高，因为本文使用流密钥进行加密，而文献［14］对MQ编码器每生成一个字节的码流就将其反馈到密钥发生器进行重新迭代，因混沌映射的高精度迭代次数太多导致加密时间太长，降低了整个系统的运行效率。相对于后者，本文提出算法的图像重构质量PSNR值提高了2 dB，因为本文引入MQ编码器进行再压缩，而文献［12］先对小波系数加密，使得小波变换后各子带系数间的相关性被破坏，从而降低了图像的压缩效率。

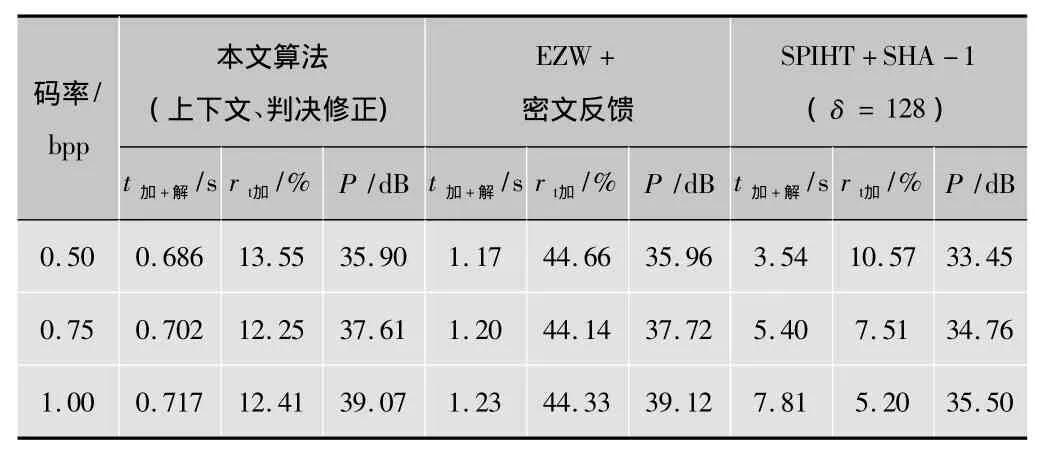
表6 本文算法与其他算法的比较

4.4 分辨率选择性加密

本文为不同分辨率的小波子带系数分配了不同的密钥初始值，实现了分辨率选择性加密。对上下文和判决进行修正，采用Pepper图像进行测试，不同分辨率级数l密钥错误时的重构图像相对于正确解密时的效果如图7所示。由图7可知，重构图像的视觉质量随子带分辨率的降低而下降，因为离散小波变换使得图像的能量分布随子带分辨率的降低而增加。因此，三级子带密钥出错使得重构图像的视觉质量最差。