一类具有时滞和非线性发生率的SIRS传染病模型稳定性与Hopf分岔分析*
2014-09-17陈方方洪灵
陈方方 洪灵
(西安交通大学机械结构强度与振动国家重点实验室,西安 710049)
一类具有时滞和非线性发生率的SIRS传染病模型稳定性与Hopf分岔分析*
陈方方 洪灵†
(西安交通大学机械结构强度与振动国家重点实验室,西安 710049)
研究了一类具有时滞及非线性特性发生率的SIRS传染病模型,首先利用特征值理论分析了无病平衡点和地方病平衡点的局部稳定性;并以时滞τ作为分岔参数,分析了模型的Hopf分岔行为,运用中心流形定理和规范型理论给出了分岔方向及分岔周期解稳定性的计算公式;最后,数值模拟验证了理论分析结果.
稳定性, 时滞, 非线性发生率, 阶段结构, Hopf分岔
引言
K-M在1927年建立了所谓的“仓室”模型[1]后,“仓室”模型的基本思想方法一直被广泛的使用并不断地发展着,截至目前,学者已根据不同疾病的发病机理建立了不同类型的传染病模型[2],并得出了一些结论.
在以前讨论的大多数模型中,我们通常将人群分成易感染者、染病者和移出者等若干类,并假定类型中的个体无差异,即他们在被感染、隔离、接种等方面完全相同,针对这类模型的研究已有很多研究结果.但是这类模型假设的合理性与实际疾病的传播仍存在一定的差距,特别是对某些传染病或接触性疾病,在不同的年龄阶段,其传播概率有很大不同,某些类型的疾病在成人中的传播概率很大,如淋病,AIDS等,而有些疾病,如麻疹,水痘等则在儿童中的传播概率较大.因此,为了更清楚的描述疾病的传播机理,就需在相应的传染病模型中考虑阶段结构.于是,在刻画传染病模型时,具有阶段结构[3-4]的传染病模型能更好地反映生物个体的生理特征和疾病的传播机理,引起了很多学者的关注,且具有重要的生物学意义.
依靠媒介传染病毒的传染病也非常多,它通过病毒、原虫或细菌等生物载体传播的,如疟疾通过蚊子来传播.Cooke在文[5]中给出了一种通过媒介传播疾病的数学模型,该建模思想在以后的建模中被广泛应用.
为方便起见,我们假定由于疾病的影响,染病的成熟个体没有繁殖能力;易感染人群仅仅被媒介染病者所感染,媒介和人群充分混合.在该假设下,我们基于文[6],建立了具有阶段结构和非线性发生率的SIRS时滞传染病模型,研究模型的平衡点的局部稳定性,分析其复杂的动力学行为.
1 模型的建立
本章所建立的SIRS时滞传染病模型:
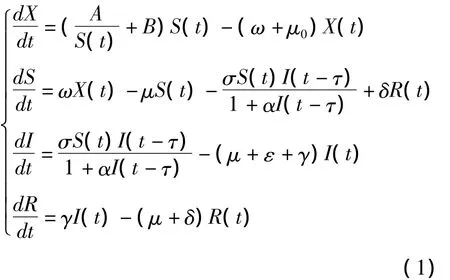
其中,X(t)为t时刻处于不成熟阶段的人口密度,S(t),I(t),R(t)为t时刻成年人中易染者、感染者和移除者的密度,ω为不成熟个体到成熟个体的转换率,μ0为不成熟个体的自然死亡率,μ为成熟个体的自然死亡率,σ为感染率,α为抑制率,ε为感染者的因病死亡率,γ为治愈率,δ为已免疫的个体重新获得易感染能力的概率,τ为疾病的潜伏期.
2 平衡点的存在性
由于模型(1)的形式较复杂,为方便讨论,我们对模型进行简化.对(1)进行无量纲化和变量替换:
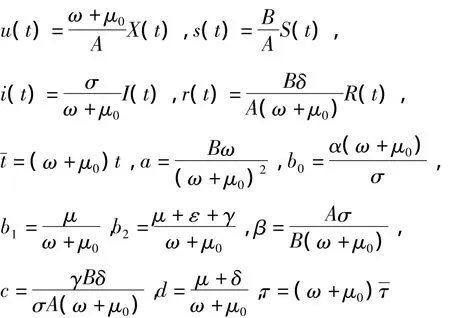
得简化后的模型为:
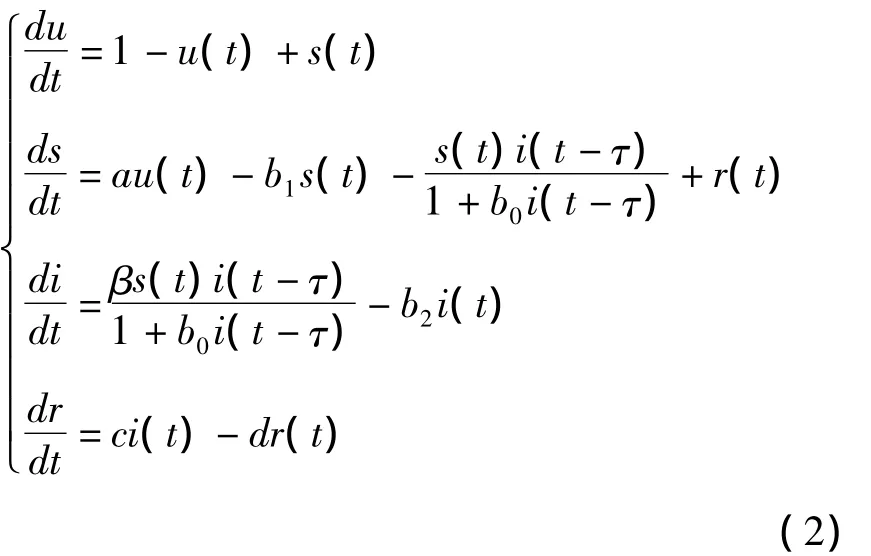
模型(2)的初始条件为:
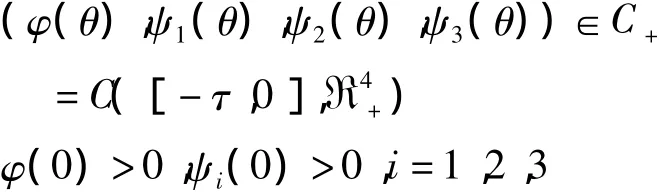
其中:ℜ4+={x1,x2,x3,x4∈ℜ4:xi≥0,i=1,2,3,4}
定义基本再生数:
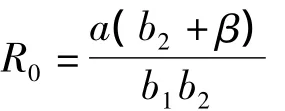
经直接计算得,系统(2)存在无病平衡点:
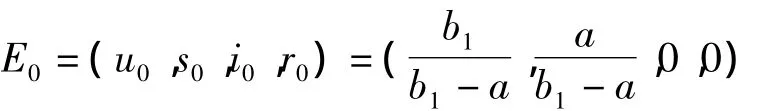
对地方病平衡点的存在性,我们有如下性质:
性质 模型(2)有唯一正平衡点E*=(u*,s*,i*,r*)当且仅当以下条件成立:
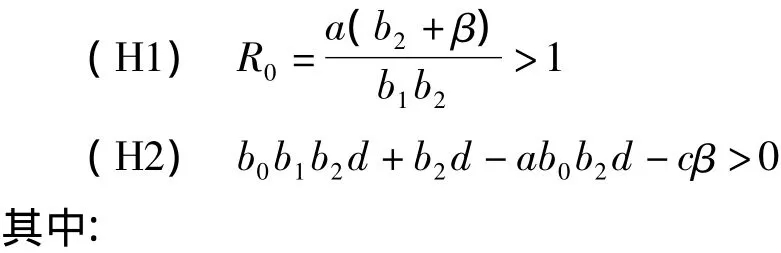
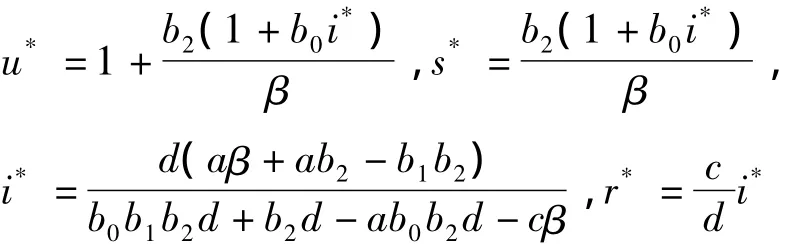
3 平衡点的稳定性
3.1 无病平衡点的局部稳定性
由平衡点的生物学意义得,若存在无病平衡点,则无病平衡点应为正,即b1>a.因此,有如下定理:
定理1 假设R0<1,对任意的τ≥0,E0局部渐近稳定的;R0>1成立,对任意的τ≥0,E0不稳定的.证明: 系统(2)在无病平衡点E0附近线性化系统的特征方程为:
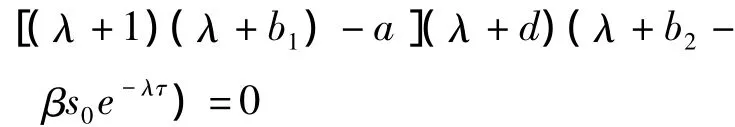
易证,当R0<1时,特征根均具有负实部;当R0>1时,至少存在一个具有正实部的特征根,因此得证.
3.2 地方病平衡点的局部稳定性
定理2 假设R0>1成立,且τ=0时,系统(2)的地方病平衡点E*局部渐近稳定.
证明: 当τ=0时,系统(2)在地方病平衡点E*附近线性化系统的特征方程为:
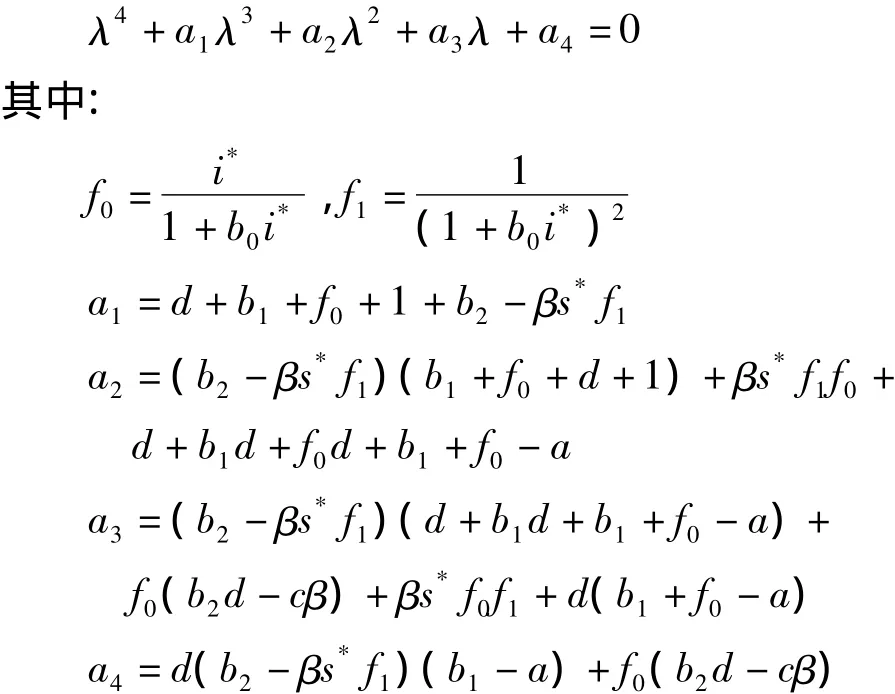
根据 Routh-Hurwitz判据,易证:当R0>1 时,a1>0,且有H1,H2,H3>0.故 τ=0 时,特征根均具有负实部,地方病平衡点E*局部渐近稳定.
定理3 当 τ>0时,若aβ+b1b2<ab2,则E*条件稳定.
证明: 当τ>0时,系统(2)在地方病平衡点E*附近线性化系统的特征方程为:
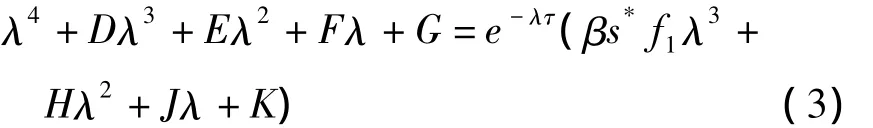
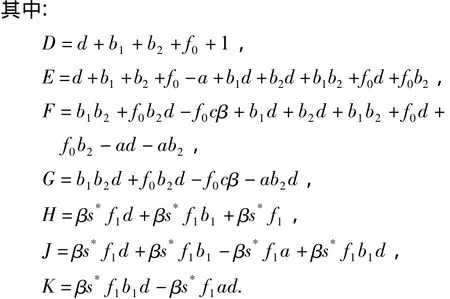
由aβ+b1b2<ab2得R0>1,已有结论,当 τ=0时系统特征根均具有负实部.以下证明特征方程(3)有唯一一对纯虚根 ±iω0(ω0>0),假定对 τ >0,iω0(ω0>0)是(3)的根,代入(3)得:
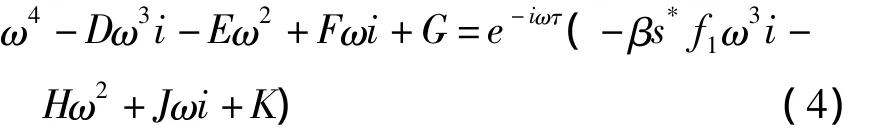
分离实部虚部得:
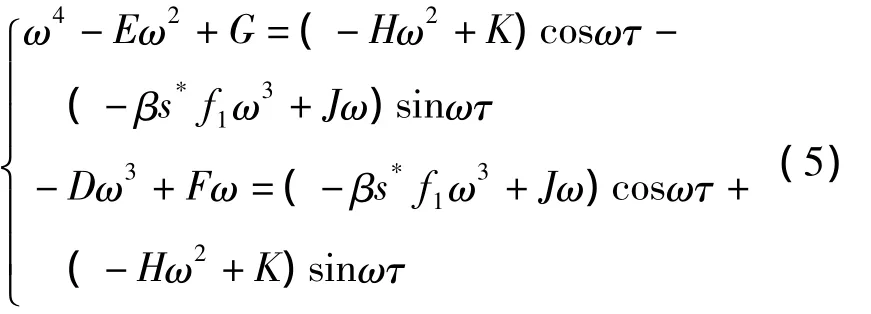
将上式两边分别平方相加得:
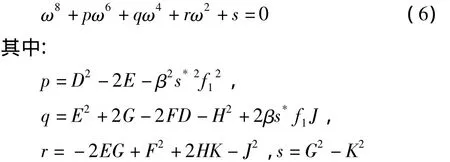
当R0>1时,我们可证得:p>0,q>0.由条件aβ+b1b2<ab2,易得s<0,由引理 2.1[6]得:(6)式存在唯一的正根ω0,即特征方程(3)存在唯一一对纯虚根,由此可得到τk>0,使得有一对纯虚根.
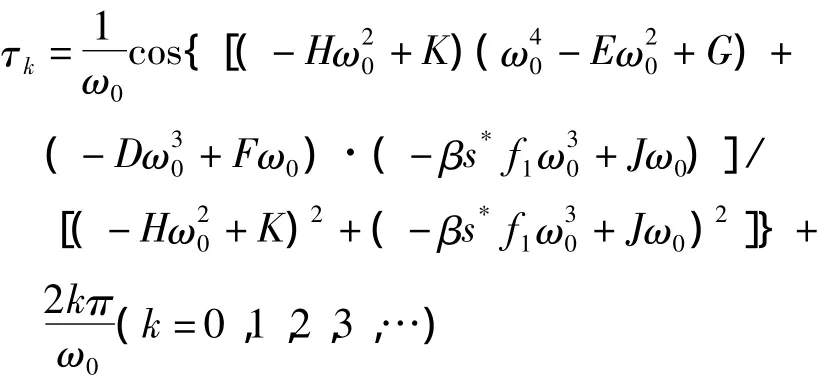
由引理2.3[7],于是我们完成了定理3的证明.以下我们将证明:
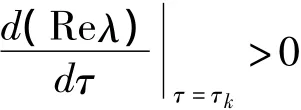
这意味着,在τ>τk时,至少存在一个具有正实部的特征根.将特征方程(3)对τ微分可得:
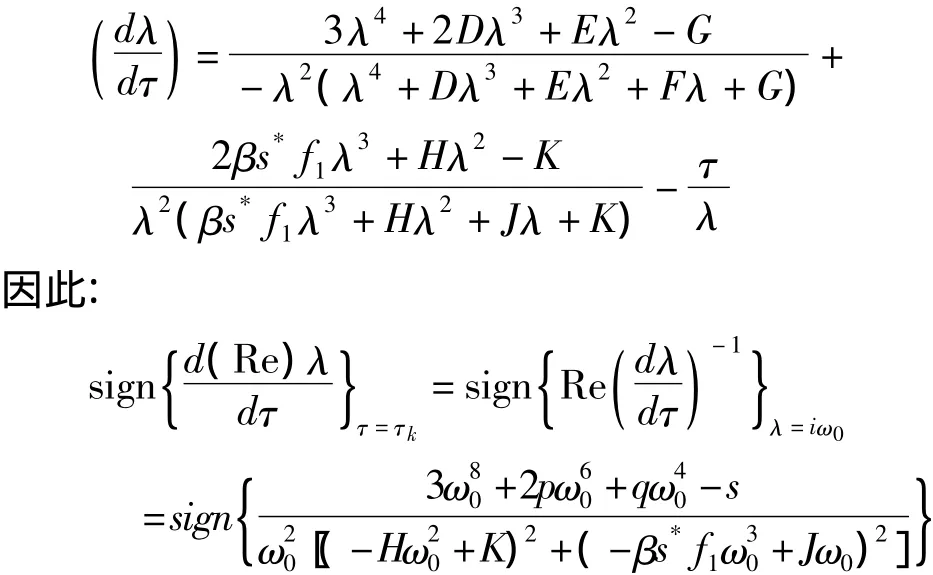
根据 Rouché's定理[8]得,时滞量 τ 由小于 τk的值增加到大于τk的值时,特征方程(3)的特征根,从虚轴左侧穿过虚轴到达虚轴右侧,横截条件成立,因此,满足 Hopf分岔条件[9],在 τ=τk处发生了Hopf分岔.
4 Hopf分岔方向和分岔稳定性
对模型(2),运用中心流形定理和规范型理论[10]给出系统(2)的Hopf分岔方向及分岔周期解的稳定性和周期计算公式.令:
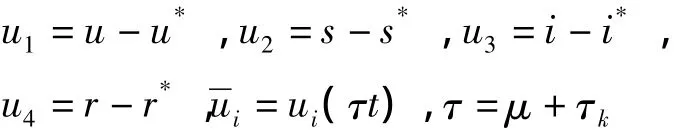
为方便起见,去掉“—”,则系统(2)可以写成C=C([-1,0],R4)上的泛函微分方程:
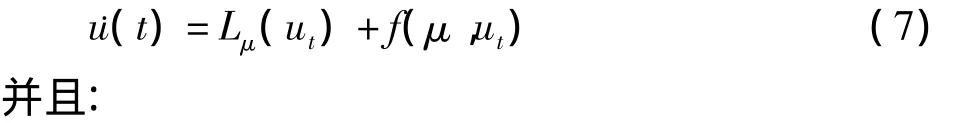

f:R×C→R4,Lμ:C→R4分别表示为:由Riesz表示引理得:对 θ∈[0,1],存在一个有界变差函数 η(θ,μ),使得:
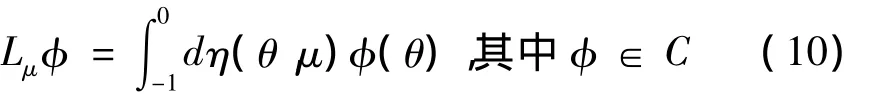
实际上,可选取:
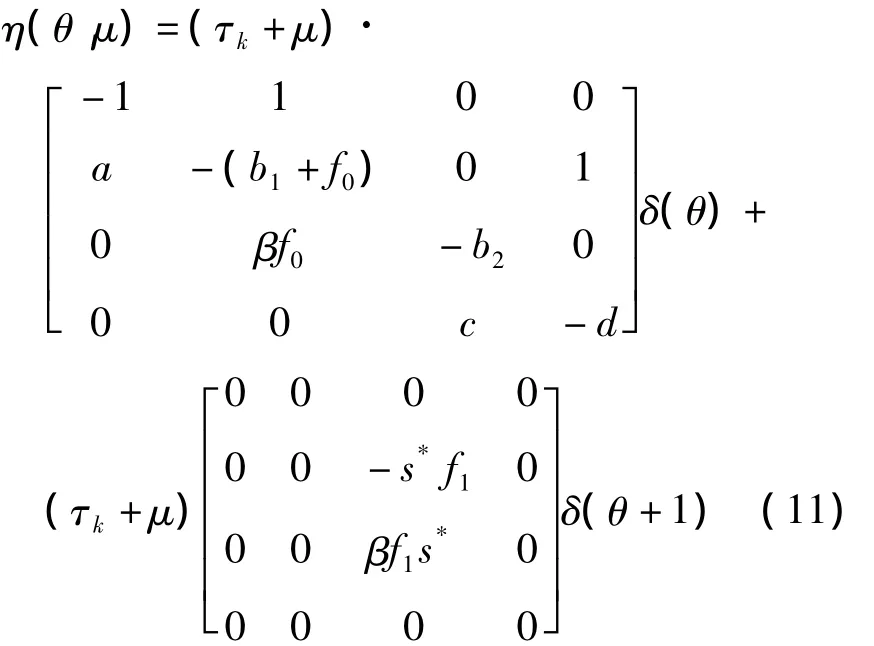
其中δ(.)表示Dirac Delta函数.
对于 φ =(φ1,φ2,φ3,φ4)T∈C[-1,0],R4),定义:
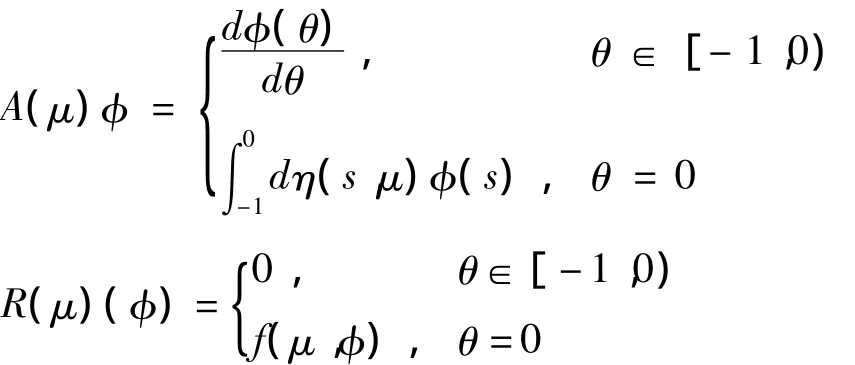
因此,系统(7)可化为:
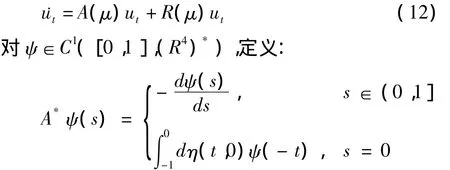
和双线性内积:
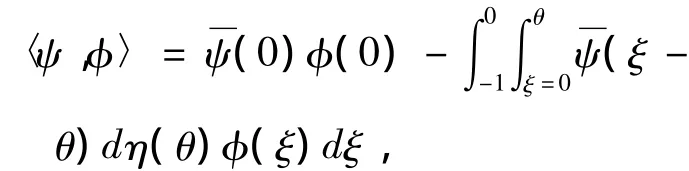
显然,A和A*为共轭算子.±iω0τk是A(0)的特征值,也是A*的特征值.下面计算A和A*关于iω0τk和 -iω0τk的特征向量.q(θ)=(1,q1,q2,q3)Teiω0τkθ是A(0)特征向量,有A(0)q(θ)=iω0τkq(θ),根据A(0)定义及式(9)(10)(11)可解得:
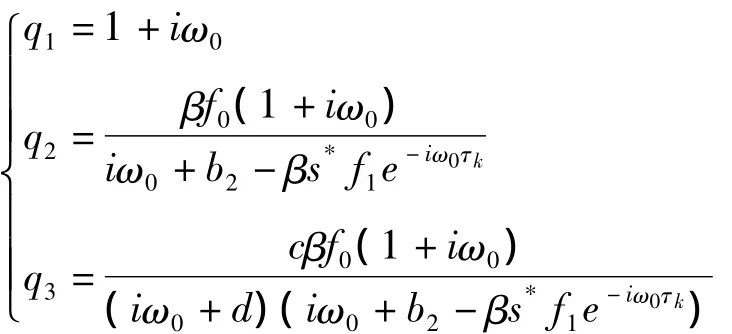
A*对应特征向量为q*(s)=D(1,)
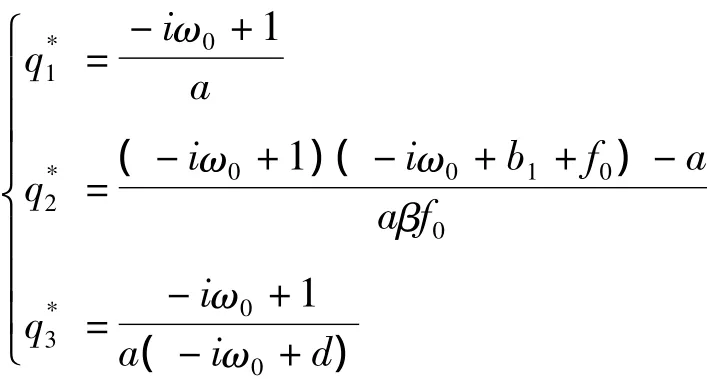
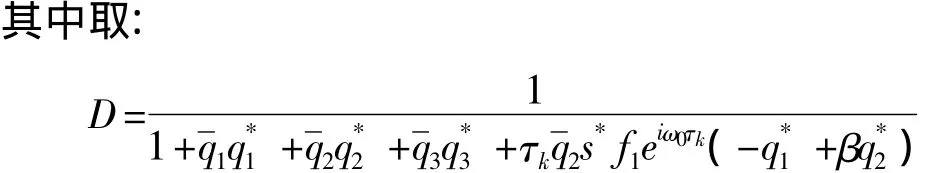
确保〈q*(s),q(θ)〉=1.接下来计算在 μ=0决定中心流形C0的坐标,令μ=0时(12)的解为ut,定义:
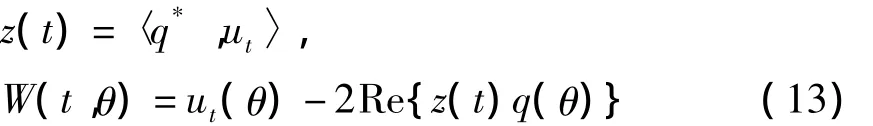
在中心流形C0上,我们有
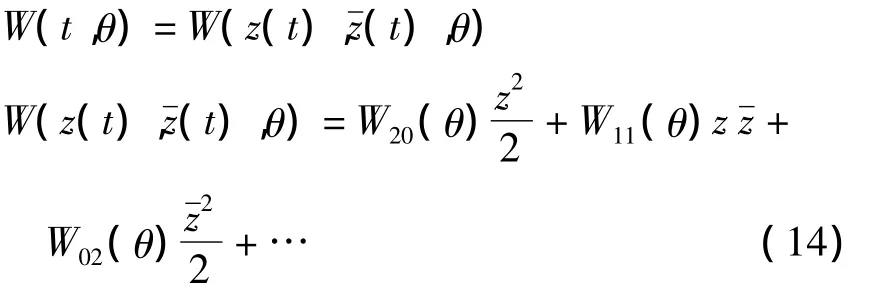
z和表示q*和上中心流形C0的局部坐标.
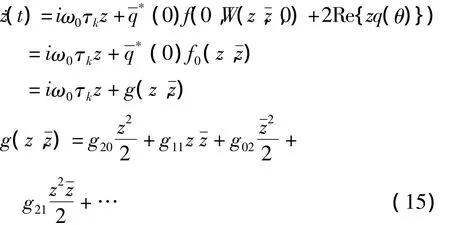
由式(13)和(14)得:
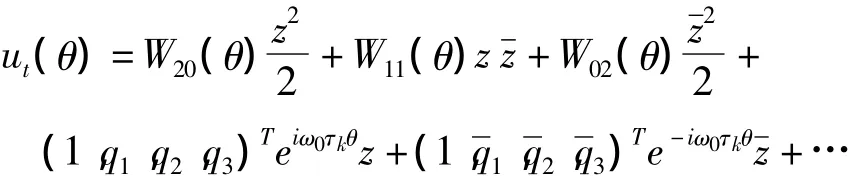
连同式(8)得:
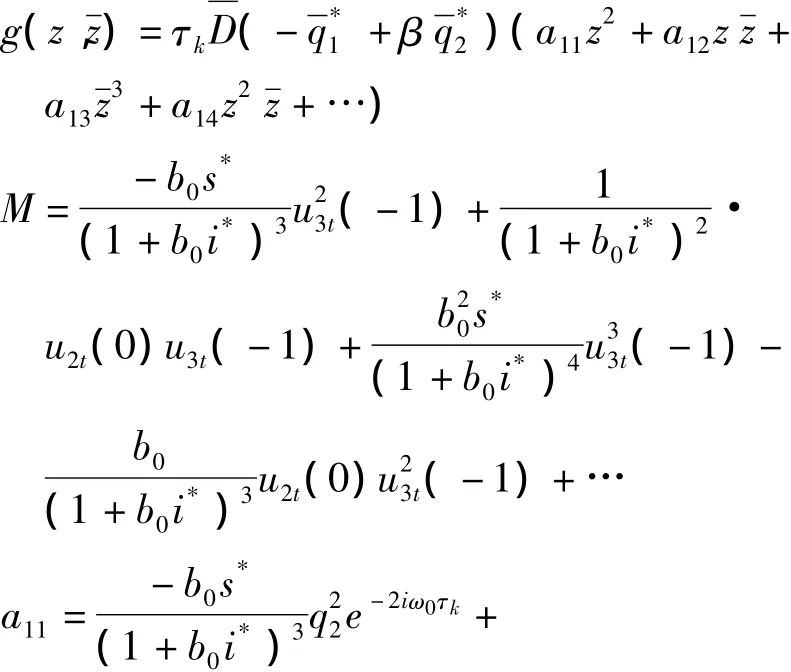

下面需要计算W20(θ)和W11(θ),由式(12)(13)得:
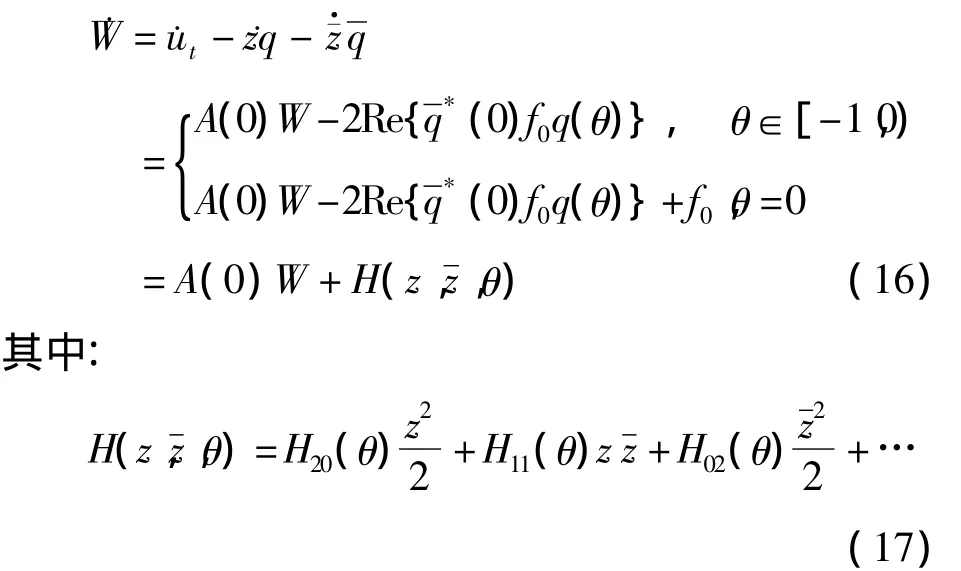
将式(17)代入式(16),并比较系数得:
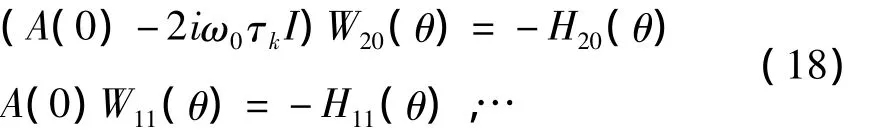
比较式(15)和式(17)的系数得:
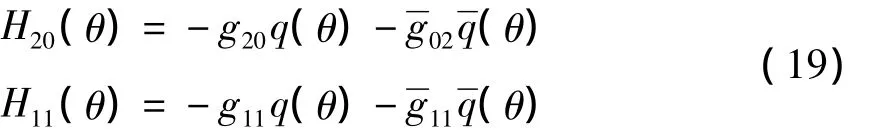
由A(0)的定义及式(18)和(19)得:
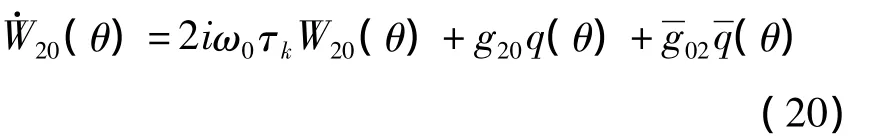
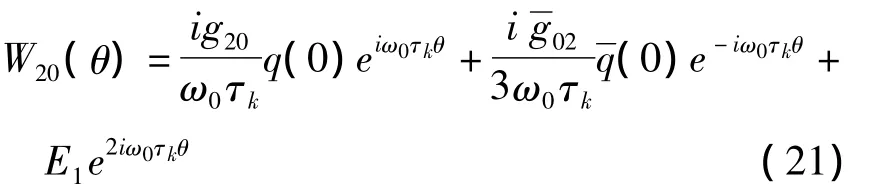
类似地,由式(18)和式(19)得:
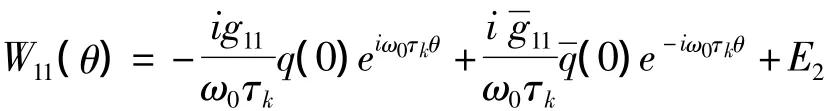
接下来,计算E1和E2的值.由A(0)及式(18),有:
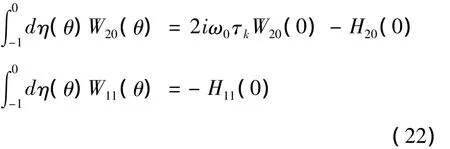
由式(16)得,当θ=0时,

此时,将式(20)和式(23)代入式(22),可求得E1.类似将式(21)和(24)代入式(22),可求得E2.因此,可得如下计算公式:
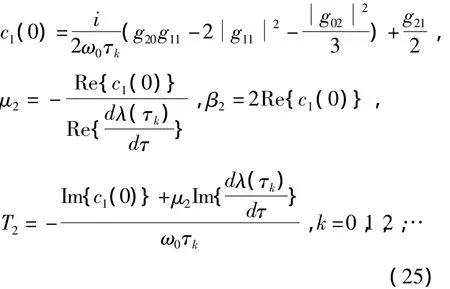
根据计算所得结果,给出如下结论:
定理4 (1)μ2决定了Hopf分岔的方向:若μ2<0(>0),则系统(2)产生次临界(超临界)的Hopf分岔,且在τ<τ0(τ>τ0)时存在分岔周期解;(2)β2决定了Hopf分岔周期解的稳定性,若β2>0(<0),则周期解是不稳定(稳定)的;(3)T2决定了分岔周期解的周期,若T2<0(>0),则分岔周期解的周期随τ的增加而减少(增加)的.
5 数值模拟
在系统(2)中,取a=2.5,b0=0.1,b1=0.5,b2=2.5,β =1.2,c=0.5,d=0.6 时,通过式(25)给出的计算公式,结合推导过程,可得:
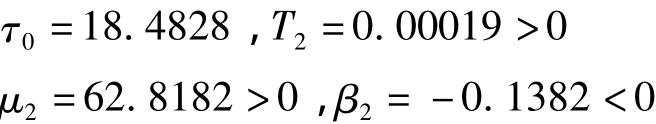
根据定理4,模型(2)在τ0处产生超临界Hopf分岔,且分岔周期解的周期是稳定的,分岔周期解的周期将随τ的增加而增加.进一步的数值模拟结果为:
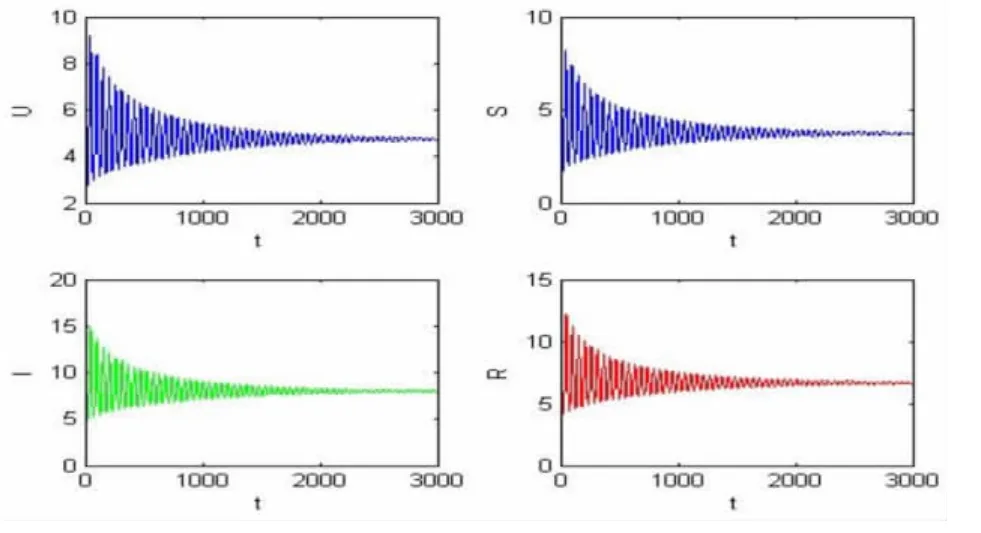
图1 地方病平衡点的时间历程图(τ=17.5)Fig.1 time history of the endemic equilibrium when τ=17.5
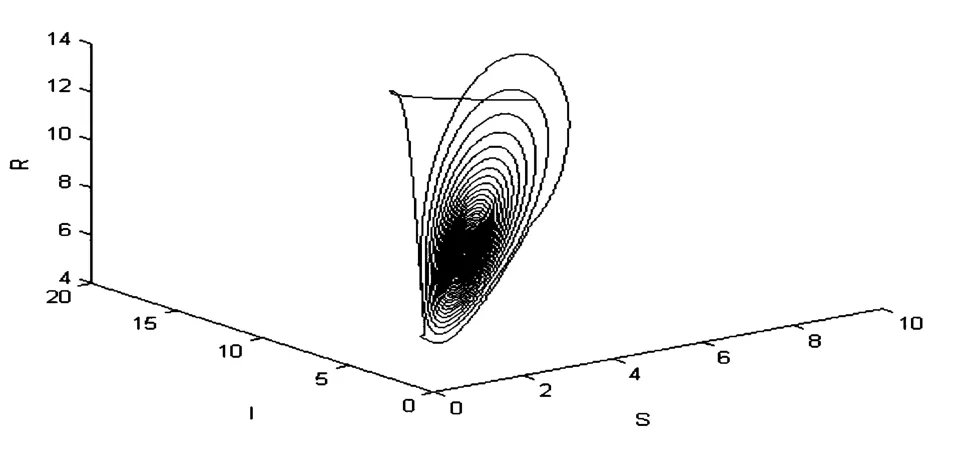
图2 地方病平衡点的相图(τ=17.5)Fig.2 phase diagram of the endemic equilibrium when τ=17.5
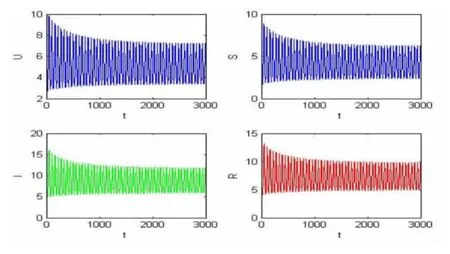
图3 地方病平衡点的时间历程图(τ=19)Fig.3 time history of the endemic equilibrium when τ=19
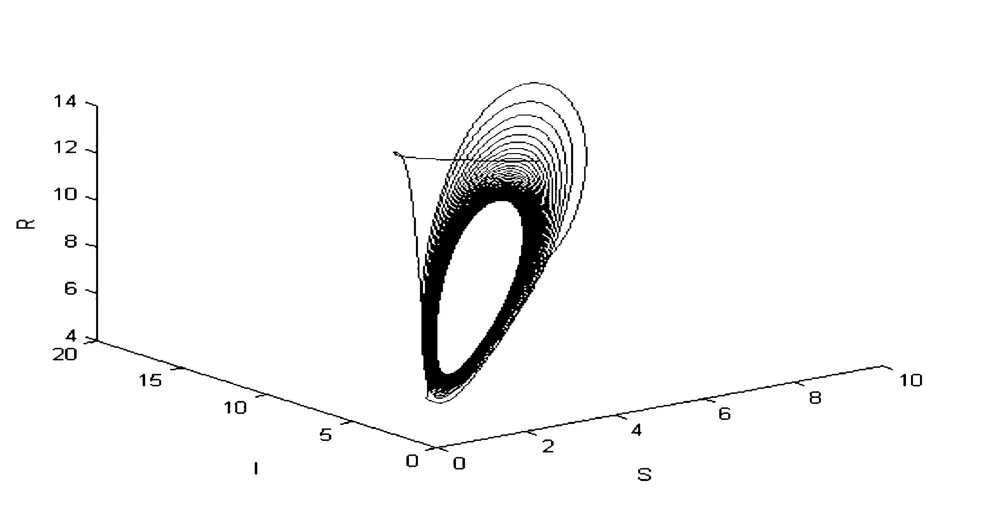
图4 地方病平衡点的相图(τ=19)Fig.4 phase diagram of the endemic equilibrium τ=19
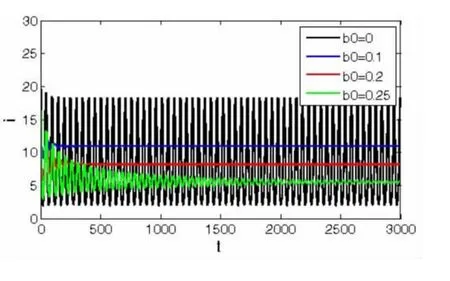
图5 不同非线性影响因素下染病个体的时间历程图Fig.5 time history of infected individuals under different nonlinear factors
6 结论
本文建立了具有非线性发生率和阶段结构的时滞SIRS模型,分析了平衡点的局部稳定性.得出:当R0<1时,对任意的τ,无病平衡点局部渐近稳定;当R0>1时,对任意的τ,无病平衡点是不稳定.对地方病平衡点稳定性分析时,在R0>1的前提下,当τ=0时,得到了地方病平衡点局部稳定的;当τ>0时,地方病平衡点条件稳定,且在τk处发生了Hopf分岔,即疾病会出现周期性爆发.
对Hopf分岔方向和分岔周期解的稳定性及分岔周期的讨论,我们运用了中心流形定理和规范型理论进行研究分析,得出系统(2)在参数满足一定的条件下,发生了超临界的Hopf分岔,分岔周期解是稳定的,且分岔周期解的周期随着时滞量τ的增加而增大.进一步的数值模拟结果,也验证了理论分析的正确性.在此基础上,为了验证非线性发生率对疾病的影响效果,通过一定的数值模拟得出,适当的增加外界抑制强度,能使染病个体的数量明显的下降,更利于治疗疾病,因此非线性发生率的引入具有非常重要的生物学意义.
1 Kermack W O,McKendrick A G.Contribution to the mathematical theory of epidemics.Proceedings of the Royal Society of London Series A,Containing Papers of a Mathematical and Physical Character,1927,115(772):700~721.
2 邵英英,刘孟,付新楚.无标度网络上分片线性传染力与免疫作用下的流行病动力学.动力学与控制学报,2009,7(3):264~269(Shao Y Y,Liu M,Fu X C.Epidemic dynamics of SIR model with piecewise linear infectivity and immunizations on scale-free networks.Journal of Dynamics and Control,2009,7(3):264 ~ 269(in Chinese))
3 Jia J W,Li Q Y.Qualitative analysis of an SIR epidemic model with stage structure.Applied Mathematics and Computation,2007,193(1):106~115
4 Lu Z H,Gao S J.Analysis of an SI epidemic model with nonlinear transmission and stage structure.Acta Mathematica Scientia,2003,23(4):440~446
5 Cooke K L.Stability analysis for a vector disease model.Journal of Mathematics,1979,9(1):31~42
6 Zhang T L,Liu J L,Teng Z D.Stability of Hopf bifurcation of a delayed SIRS epidemic model with stage structure.Nonlinear Analysis:Real World Applications,2010,11(1):293~306
7 Li X L,Wei J J.On the zeros of a fourth degree exponential polynomial with applications to a neural network model with delays.Chaos,Solitons&Fractals,2005,26(2):519~526
8 Dieudonné J A,Dieudonné J,Mathematician F.Foundations of modern analysis.New York:Academic Press ,1960
9 Hale J K,Lunel SMV.Introduction to functional differential equations.Springer,1993
10 Hassard B D,Kazarinoff N D,Wan Y H.Theory of applications of Hopf bifurcation.CUP Archive,1981
*The project supported by the National Natural Science Foundation of China(11332008)
† Corresponding author E-mail:hongling@mail.xjtu.edu.cn
STABILITY AND HOPF BIFURCATION ANALYSIS OF A DELAYED SIRS EPIDEMIC MODEL WITH NONLINEAR SATURATION INCIDENCE*
Chen Fangfang Hong Ling†
(State Key Laboratory for Strength and Vibration of Mechanical Structures,Xi'an Jiaotong University,Xi'an710049,China)
An SIRS epidemic model with nonlinear saturation incidence rate and time delay was investigated.By analyzing the corresponding characteristic equations,the local stability of disease-free equilibrium and endemic equilibrium was discussed.The bifurcation property was obtained as the time delay passed through a critical value.Applying the center manifold argument and normal form theory,some local bifurcation results were obtained and the formulas for determining the bifurcation direction and stability of the bifurcated periodic solution were derived.Numerical simulations were presented to illustrate the theoretical analysis.
stability, time delay, nonlinear incidence rate, stage structure, Hopf bifurcation
31 May 2013,
8 June 2013.
10.6052/1672-6553-2013-070
2013-05-31 收到第 1 稿,2013-06-08 收到修改稿.
*国家自然科学基金资助项目(11332008)
E-mail:hongling@mail.xjtu.edu.cn
