恒载效应对拱结构自振频率的影响分析*

康婷 许金余 白应生 孙惠香 李庆

(空军工程大学航空航天工程学院，西安 710038)

恒载效应对拱结构自振频率的影响分析*

康婷†许金余 白应生 孙惠香 李庆

(空军工程大学航空航天工程学院，西安 710038)

提出用样条有限点法分析拱的自振频率，采用3次B样条函数的线性组合作为位移振型函数，以曲杆变形理论为基础，根据Hamilton原理建立了考虑恒载效应影响时拱的振动频率方程．计算分析了恒载效应对拱结构自振频率的影响．结果表明恒载效应会使拱结构自振频率减小;影响大小与结构自身刚度有关;拱结构截面刚度一定时，拱矢跨比、径厚比越大，恒载效应对自振频率的影响越大．

拱， 恒载效应， 自振频率

引言

拱结构在振动时，同时承受着恒载的作用．因此拱结构在振动时，将从由恒载产生的初始变形状态下开始变形，使结构的后续变形减小，这就是恒载效应．恒载效应必将对拱的振动特性产生影响．

周世军［1－4］等研究了恒载效应对直梁和曲梁的自振频率的影响，发现恒载效应引起的初始弯曲应力会使梁自振频率增大．这一结论是基于纯弯曲简支梁得出的．众所周知，拱在竖向恒载作用下截面以受轴压力为主，弯矩和剪力均较小，这和梁的受力特点是完全不同的，因此这一结果并不适用于一般的拱结构．关于拱结构自振频率的研究很多［5－6］，但考虑恒载影响的很少．李保［7］等利用哈密顿原理推导出圆弧拱振动控制微分方程，用Galerkin方法研究了自重对拱自振频率的影响，但并没有分析这种影响与拱刚度、矢跨比、径厚比等因素的关系，也未考虑上覆荷载的影响．

曾有学者用样条小波有限元法分析结构的自振频率［8］，本文提出用样条有限点法，根据哈密尔顿原理建立拱振动频率方程，其中考虑了恒载效应的影响，推导出了样条有限点法的计算格式．编程计算分析了恒载效应对拱结构自振频率的影响．结果表明恒载效应会使拱结构自振频率减小，但对于一般的拱结构，自重对其自振频率的影响较小;影响大小与结构自身刚度有关;拱结构截面刚度一定时，拱矢跨比f/l、径厚比r/d越大，恒载效应对自振频率的影响越大．

1 基本方程

1．1 基本假定

(1)基于平面变形假设，变形前垂直于中线的直线，变形后仍垂直于中线;(2)忽略剪切变形的影响;(3)材料是均匀、连续、各向同性的;(4)振动是弹性的．

1．2 曲杆变形几何关系

分析时以拱的恒载变形状态作为参考状态，见图1．

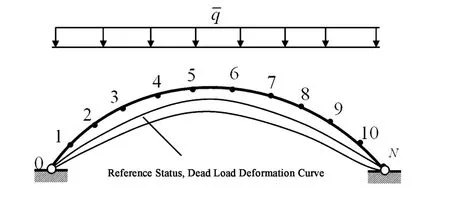
图1 拱结构样条离散化Fig．1 Spline discretization of arch

式中，u*是拱结构某一点的切向位移，以绕曲率中心顺时针转动为正和u分别表示恒载和动力活载引起的切向位移;v*是拱结构某一点的径向位移，以指向极点为正和v分别表示恒载和动力活载引起的径向位移．

根据曲杆变形理论，应变－位移具有下述关系:

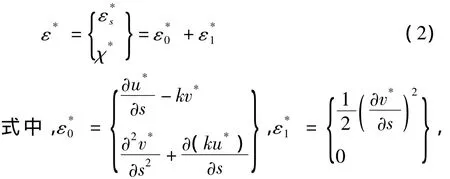
分别为线性应变部分和为非线性应变部分;其中，为拱轴向应变，以伸长为正，χ*为曲率应变．

1．3 拱振动时的泛函

根据Hamilton原理，精确解使下列泛函取驻值．

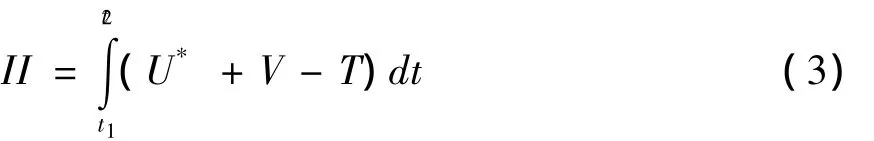
式中，U*为拱结构的应变能;V为外荷载作用下产生的势能;T为体系的动能．

在振动时，拱结构的应变能可以写为:

式中，和U分别为恒载和动力活载q作用下由于变形u、v所产生的应变能，分别定义为

式中，ε为动荷载产生的应变，ε为恒载作用下产生的应变．在计算U时使用方程(2)给出的线性应变－位移关系;而在计算时，使用方程(2)给出的线性应变－位移关系以引入恒载效应．D=diag(EA，EI)，E为弹性模量，A为截面面积．

作用在结构上的恒载产生的势能为:

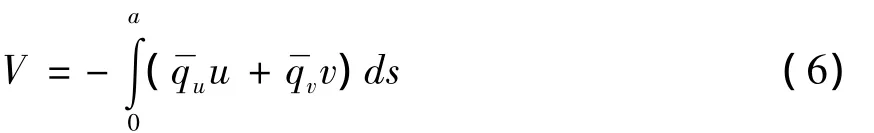
式中为恒载的切向分量为恒载的法向分量．

忽略剪力，转动惯量的影响，动能可以写为:

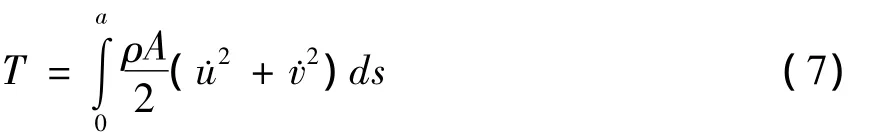
1．4 位移振型函数

拱自由振动时切向位移和径向位移可分别表示为:

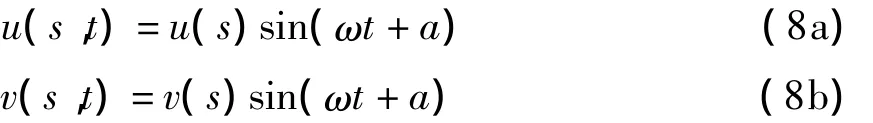
式中u(s)、v(s)分别为切向、径向位移振型函数，用三次B样条函数拟合(具体做法参见文献［8］)．

其中φi(s)为三次B样条函数构成的样条基函数．u0、v0、v'0，uN、vN、v'分别为拱左端(s0)和右端(sN)处的切向位移和径向位移及转角，由位移边界条件确定．

样条基函数的构造类似于有限元法中形函数的构造，根据拱结构位移边界条件:

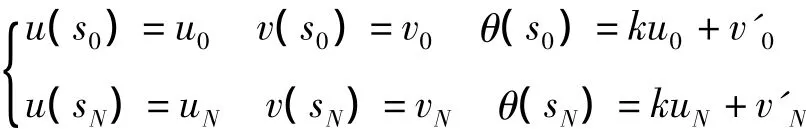
得满足边界条件的样条基函数如下式所示(具体做法参见相关文献)．

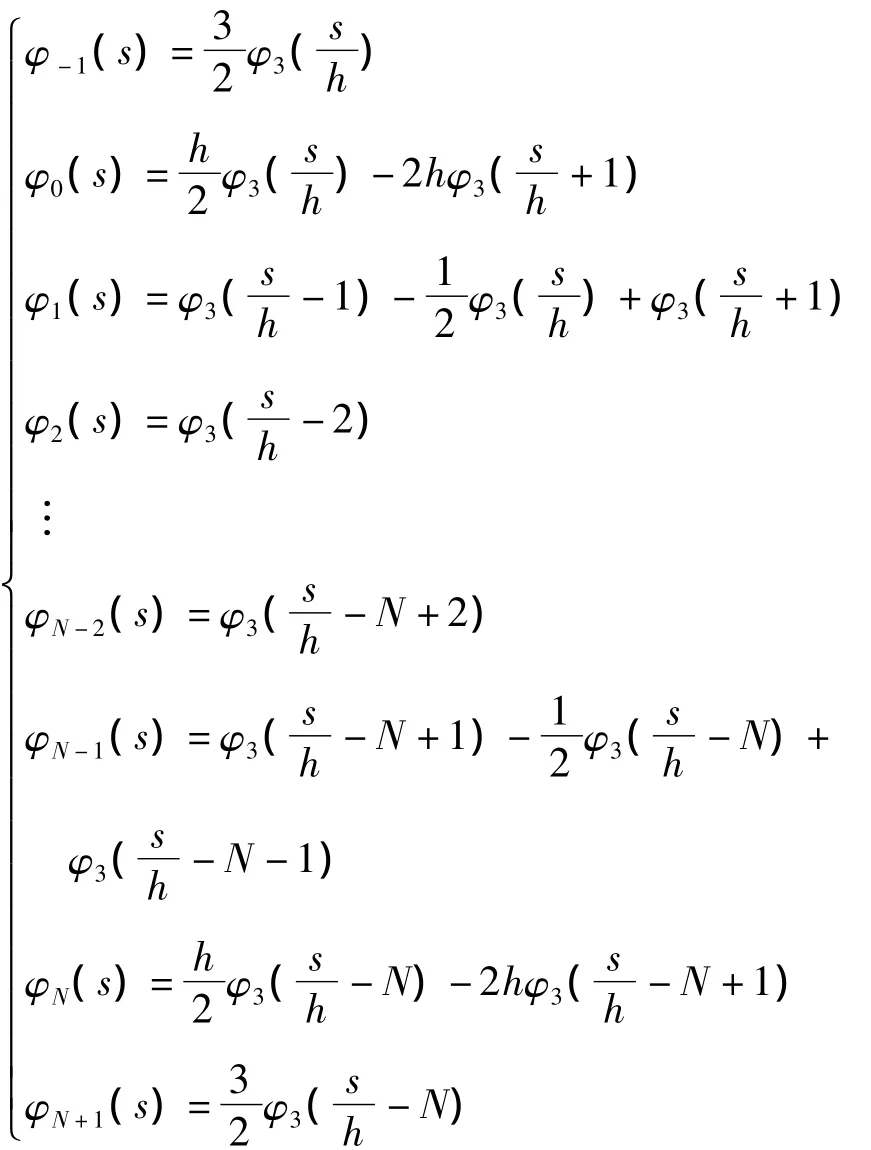
其中φ3(s)为三次样条函数，这组基函数有下列特点:

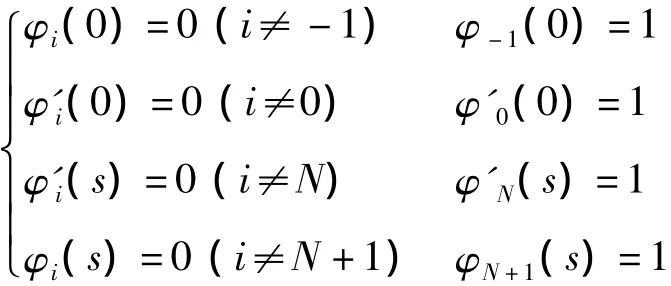
1．5 频率方程

将位移振型函数式(9)代入曲杆位移与应变的几何关系式(2)，得如下式:

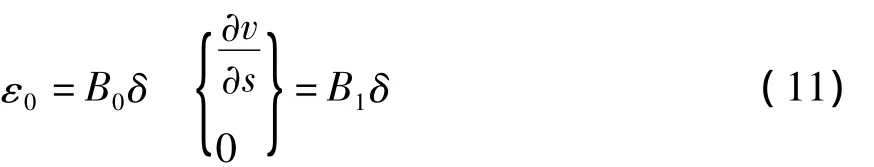
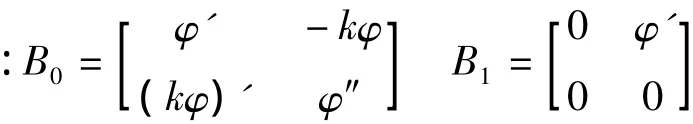
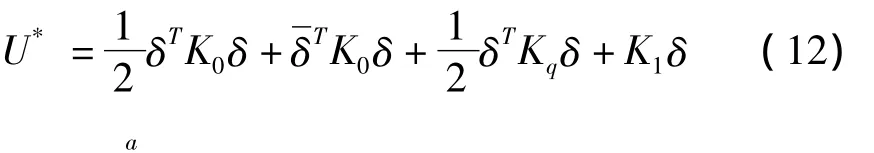
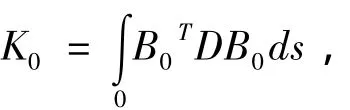
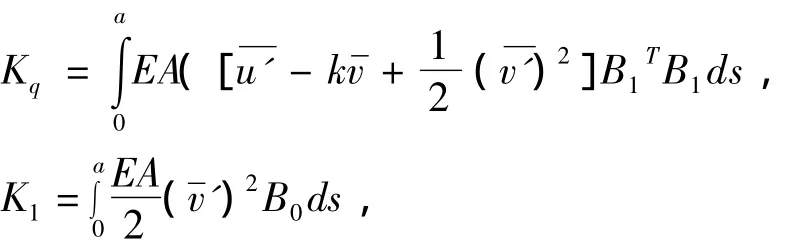
K0为一般的线性刚度矩阵;Kq和K1为由于恒载的影响而产生的刚度矩阵．

作用在结构上的恒载产生的势能为:

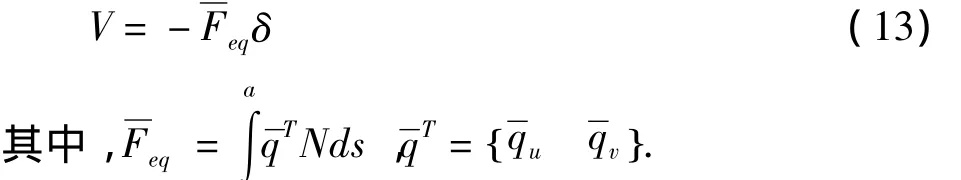
假定积分时间取为一个周期，根据变分原理可得下列方程:

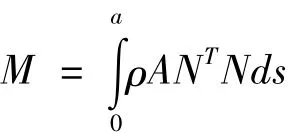
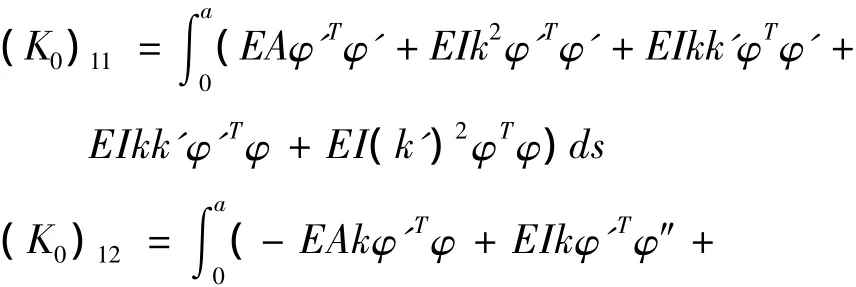
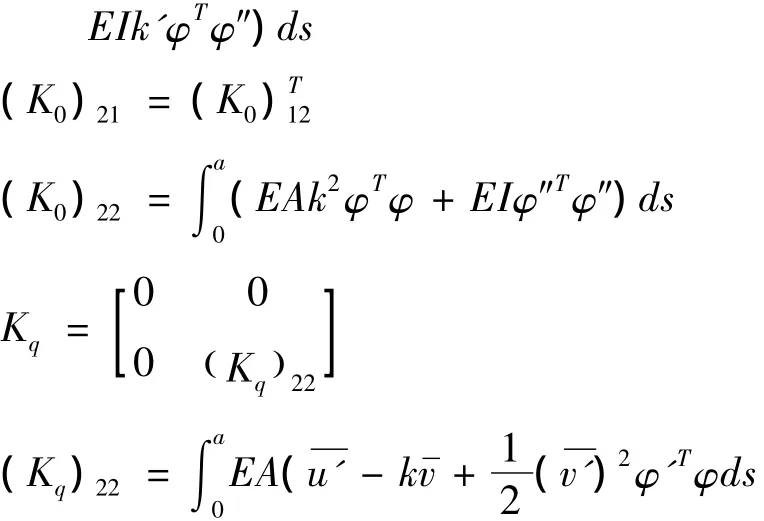
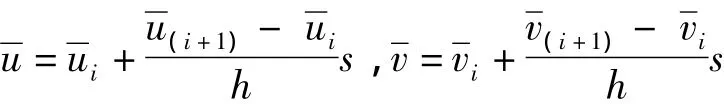
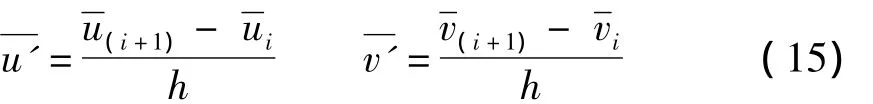
式中:h为第i单元的弧长，s为第i曲杆单元内某点距端点i的弧长是由外荷载引起的，由样条有限点法求得．

2 频率计算分析

当曲率k→0时，式(14)即转化为梁在恒载影响下的振动频率方程．为了验证本文方法的正确性、通用性和使用精度，对文献［2］中的简支梁进行了计算．材料为16Mn钢，梁跨度L=10m，矩形截面 A=b×h=0．3m ×0．4m，EI=3．36 ×108N·m2，外荷载=150kN/m．ω1为考虑恒载效应的最小频率，ω01为不考虑恒载效应的最小频率．ω1/ω01的计算结果为 1．1054，文献［2］的结果为 1．0918，文献［1］的结果为1．1081．由此说明本文方法具有足够的精度，且具有通用性．考虑横载效应会使梁自振频率增大．

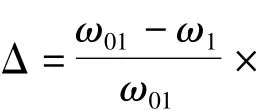
一般工程中，拱结构上除了自重还有外荷载作用．设拱为矩形截面A=b×h=1m×0．5m，均布质量=1250kg/m，自重=12．5kN/m，其他参数与上述拱相同．外荷载为q=a q1．恒载效应对自振频率的影响随失跨比的变化关系如图3所示．图4为a=6，即外荷载为自重荷载的6倍，不同径厚比(自重各不相同)时的计算结果．

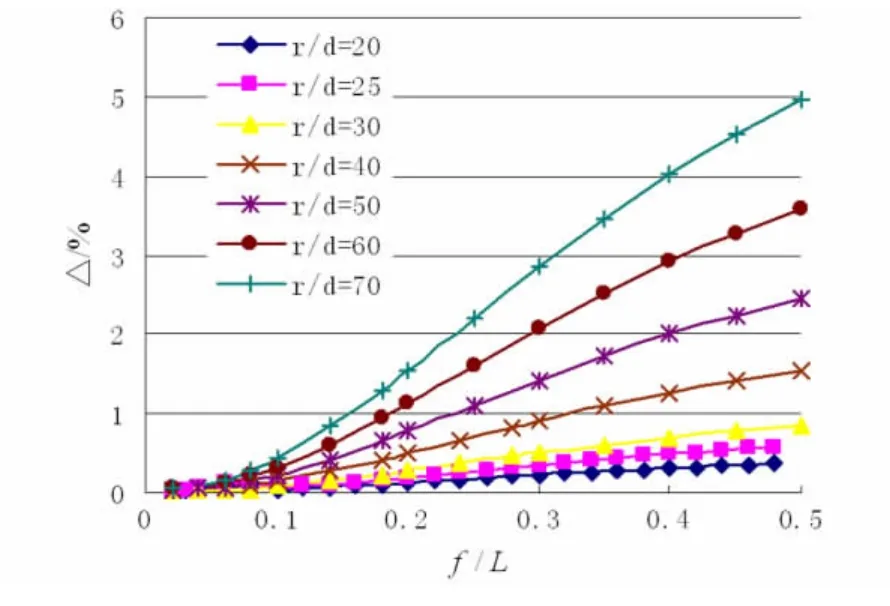
图2 不同径厚比时恒载效应对拱最小频率的影响Fig．2 Effects of dead loads on minimum frequency of arch

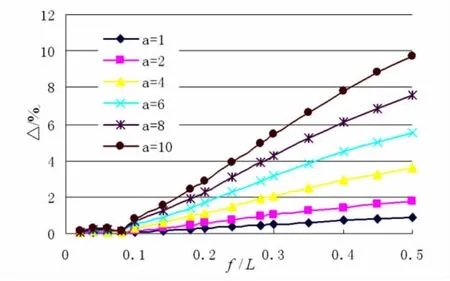
图3 不同外荷载时恒载效应对最小频率的影响(r/d=30)Fig．3 Effects of dead loads on minimum frequency of arch

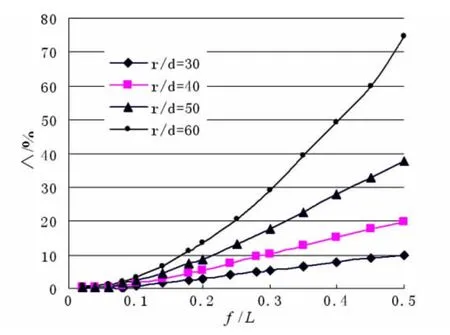
图4 恒载效应对最小频率的影响(a=6)Fig．4 Effects of dead loads on minimum frequency of arch

从图2中可以看出，考虑自重使拱的自振频率减小．减小的幅度随着矢跨比、径厚比的增大而增大．但总的来说，若没有上覆荷载，拱自重对最小频率的影响较小．若径厚比 r/d＜70，矢跨比 f/l＜0．5，不计自重的影响引起的误差不超过5%．

从图3可以看出，外荷载越大，频率减小得越多．当然外荷载不能无限制增大，当外荷载增大到使结构刚度矩阵出现负值时，这实为拱结构静力稳定的动力判据，这时的外荷载实为拱结构静力稳定极限承载力．a≤4时，恒载效应引起的频率误差不超过5%．若这时的外荷载叫临界外荷载，则径厚比、矢跨比越大，临界外荷载越小．

从图4中可以看出，即使外荷载很大(a=6)，当失跨比f/l＜0．1时，恒载效应对拱结构的最小频率影响很小．事实上恒载效应对拱自振频率的影响大小主要取决于轴向力对自振频率的影响．这时拱的曲率很小，拱的振动主要以横向振动(弯曲)为主，拱纵向振动(拉压)的影响很小，类似于梁的横向振动，因此轴向压力对最小自振频率的影响很小．当f/l→0即k→0时，方程(13)化为两个完全独立的方程，分别代表梁的横向振动和纵向振动，从刚度矩阵Kq」22的计算即可发现，恒载效应(横向)会使梁自振频率增大，与文献［2］的结论一致．

3 结论

本文用样条有限点法分析拱的动力问题，采用3次B样条函数的线性组合作为位移振型函数，以曲杆变形理论为基础，根据哈密尔顿原理建立了考虑恒载效应影响时拱的振动频率方程．编程计算分析了恒载效应对拱结构自振频率的影响，本文方法对梁具有通用性．结果表明恒载效应会使拱结构自振频率减小;拱上恒载越大，频率减小得越多;但对于一般的拱结构，自重对其自振频率的影响较小;影响大小与结构自身刚度有关;当外荷载增大到使拱结构刚度方程出现负值时，这实为拱结构静力稳定的动力判据;拱结构截面刚度一定时，拱矢跨比f/l、径厚比r/d越大，恒载效应对自振频率的影响越大，这种影响总是减小了拱的自振频率．

1 Takabatake H．Effects of dead loads on natural frequencies of beams．Journal of Structural Engineering ASCE，1991，117(4):1102～1120

2 周世军，朱唏．恒载对梁自振频率影响的分析．铁道学报，1995，17(4):98～103(Zhou S J，Zhu X ．Analysis of effect of dead loads on natural frequencies of beams．Journal of the China Railway Society，1995，17(4):98 ～103(in Chinese))

3 Zhou S J，Zhu X．Analysis of effect of dead loads on natural frequencies of beams using finite element techniques．Journal of Structural Engineering ASCE，1996，122(5):512～516

4 张家玮，周世军．恒载效应对拱形梁自振频率的影响分析．振动与冲击，2009，28(8):163～167(Zhang J W，Zhou S J．Analysis of effect of dead loads on natural frequencies of beams．Journal of Vibration and Shock，2009，28(8):163～167(in Chinese))

5 薛祖卫．抛物线拱的反对称和对称的固有振动．土木工程学报，1963，9(5):142～144(Xue Z W．Parabolic arch of the antsymmetric and symmetric vibration inherent．Civil Engineering Technology，1963，9(5):142 ～144(in Chinese))

6 钱七虎等．拱型结构的自振频率计算及轴向变形对自振频率的影响．钱七虎院士论文选集，1999，153～160(Qian Q H．Arch natural frequency calculation and affection of the axial deformation on the natural frequency．Qian Qihu Academician TECHNOLOGY，1999，153 ～160(in Chinese))

7 李宝，刘洪兵，张春燕．重力影响条件下拱的振动分析．低温建筑技术，2005，103(1):52～54(Li B，Liu H B，Zhang C Y．Vibration analysis of arch under the influence of gravity load ．Low Temperature Architecture Technology，2005，103(1):52 ～54(in Chinese))

8 陈新锋，徐建新，卿光辉．层合板固有频率分析的B样条小波元法．动力学与控制学报，2009，7(1):50～54(Chen X F，Xu J X，Qing G H．Bspline wavelet finite element method for analyzing natural frwquencies of laminated plates．Journal of Dynamics and Control，2009，7(1):50 ～54(in Chinese))

*The project supported by the National Natural Science Foundation of China(51308540，51208506)

† Corresponding author E－mail:bysapple@126．com

SPLINE FINITE POINT METHOD FOR ANALYZING THE EFFECT OF DEAD LOADS ON NATURAL FREQUENCIES OF ARCH*

Kang Ting†Xu Jinyu Bai Yingsheng Sun Huixiang Li Qing
(The Aeronautics and Astronautics Engineering Institute，Air Force Engineering University，Xi'an710038，China)

A spline finite point method was presented to study the natural frequency of arch．The displacement mode shape function of the arch free vibration was simulated with a linear combination of cubic B－spline．The free vibration frequency equation of arch structures was derived according to Hamilton principle，in which the effect of the dead load was considered．Meanwhile，the effect of the dead load on the natural frequency of arch structures was analyzed．The results show that the natural frequency of arch is reduced．The effect of influence depends on the stiffness of the arch itself．When the arch stiffness is certain，the bigger the rise span ration and the radius to thickness ration，the higher the effect of the dead load on the natural frequency of arch structures．

arch， effect of dead loads， natural frequency

5 December 2012，

17 December 2012．

10．6052/1672－6553－2013－097

2012－12－05 收到第 1 稿，2012－12－17 收到修改稿．

*国家自然科学基金资助项目(51308540，51208506)

E－mail:bysapple@126．com