非高斯噪声驱动的耗散动力系统的信息熵演化*

郭永峰 赵小山 谭建国

(1．天津工业大学理学院，天津 300387)(2．天津职业技术师范大学理学院，天津 300222)

非高斯噪声驱动的耗散动力系统的信息熵演化*

郭永峰1†赵小山2谭建国1

(1．天津工业大学理学院，天津 300387)(2．天津职业技术师范大学理学院，天津 300222)

熵在描述随机系统的演变、不稳定性、无序性或混乱程度以及信息传递方面起着重要的作用．本文对非高斯噪声驱动的一类耗散动力系统的信息熵演化进行了研究，文中通过线性变换的方法简化了所研究系统的FPK方程，然后根据Shannon信息熵定义推导出了该耗散动力系统随时间演化信息熵的精确表达式，最后分析了非高斯噪声和系统耗散参数对系统信息熵的影响．

信息熵， 非高斯噪声， 耗散动力系统， Fokker－Planck方程

引言

熵的概念是针对孤立系统准静态自然演变的定量描述而引入的，它在描述随机系统的演变、不稳定性、无序性或混乱程度以及信息传递方面起着重要的作用．1948 年，Shannon［1－2］将物理学中的数学统计方法移植到通信领域提出了信息熵的概念．信息熵的提出使熵的应用范围也有了迅速而广泛的发展，已经远远超出了热力学和统计物理学的范畴，熵在数学、化学、宇宙学、生物学、信息论、控制论、经济学、社会学及各种工程科学等领域中发挥出越来越重要的作用．人们可借助对宏观系统熵的研究来更好的了解系统的微观变化状态．

实际上，无论从信息传递的角度还是从动力学系统有序度和无序度的角度来看，信息和信息熵总是随时空过程变化的［3－4］．熵作为表征不可逆过程自发趋势的限度，表现为在一定条件下具有某种极值性质．从动力系统的角度看，信息熵的动态性是客观的，非平衡信息熵随时间的演化规律及噪声性质对其影响的研究备受关注［3－15］．D．Daems和 G．Nicolis［5］研究了高斯白噪声驱动的动力学系统中信息熵产生与相空间体积收缩的关系．Bag等［6－11］探讨了高斯色噪声或关联高斯白噪声驱动的动力学系统中噪声性质及系统的耗散参数对Shannon信息熵流、熵产生和熵变化率上界的影响，并考虑了经变换后Fokker－Planck(FPK)方程可精确求解的几类典型动力学系统，得到了Shannon信息熵流、熵产生和熵变上界随时间演化的精确表达式．文献［12－14］对准单色噪声及色噪声驱动的一类动力系统的信息熵演化、熵流与熵产生和熵变化率上界等现象进行了相关探讨．

由于噪声的性质对系统的信息熵演化、熵流与熵产生以及熵变化率上界有着显著的影响，因此研究由不同性质的噪声对其所驱动的动力系统的影响有着十分重要的意义．然而，在上述的研究中人们主要考虑的是高斯噪声，非高斯噪声所驱动的动力系统的信息熵演化现象值得进一步研究．文献［15－21］分别对非高斯噪声驱动的动力系统的熵流与熵产生、稳态概率密度、随机共振等相关问题进行了探讨．那么非高斯噪声对其所驱动的耗散动力系统信息熵演化的影响将会是怎样的呢?本文将在已有的研究基础上对这一问题进行探讨．

1 非高斯噪声驱动的随机耗散动力系统

考虑下述非高斯噪声驱动的随机耗散动力学系统，其 Langevin 方程为［15］:

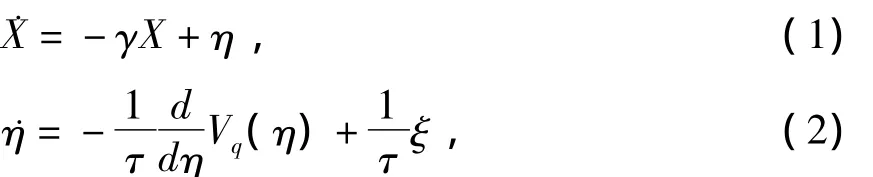
这里，η为非高斯噪声，ξ为高斯白噪声，其统计性质为

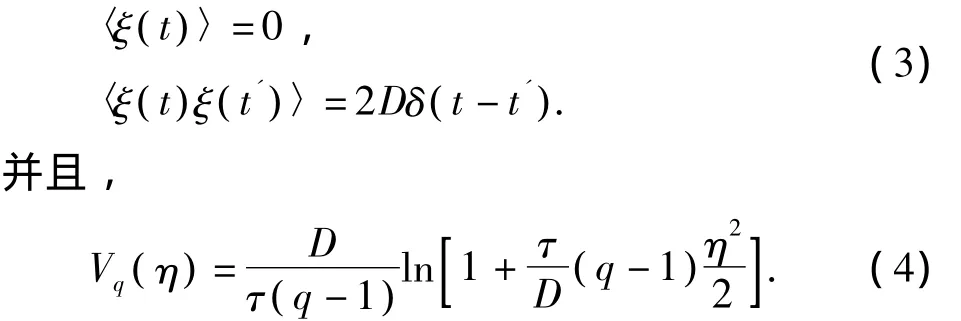
其中，参数q表示η偏离高斯分布的程度．

根据文献［16－21］可知方程(2)式的稳态概率密度为

当≪1 时，由路径积分近似［16－21］，可得

这里，τeff为有效噪声关联时间，满足

并且有效噪声强度为

显然，当q→1时，有 τeff→τ且Deff→D，方程(1)退化为由色噪声驱动的情形．

通过以上近似，(2)式就可以简化为标准的Ornstein－Uhlenbeck 过程，即

并且〈ξ(t) ξ(t') 〉=2Deffδ(t－t')．

令X1=X，X2=η，并结合(10)式可将方程(1)等效化为［15］

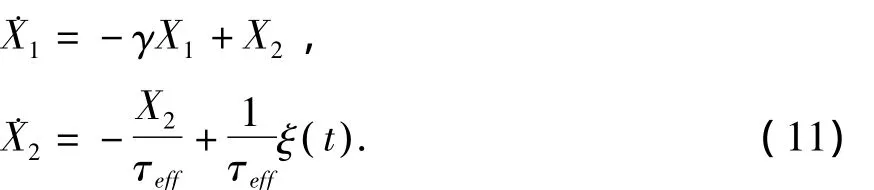
由上式可得到系统的等效FPK方程:

其中 ρ(X1，X2，t)为扩维后相空间的概率分布函数．

2 系统随时间演化的信息熵表达式

上式中，

这里，λ和a是待定常数．把U=aX1+X2代入(15)式可得到

将FPK方程(13)式写成下述形式

其中，▽U表示相空间的散度，

根据信息熵定义，取具有连续概率分布ρ(U，t)的 Shannon信息熵为

由上述Shannon信息熵定义以及(5)式和(6)式得信息熵S随时间演化的方程为

对上式右边进行部分积分，并利用边界条件［23］j=0可得

根据文献［6－12］的方法，方程(13)式解的形式可设为

根据初始条件

并将(22)式和(24)式进行对比可得

接下来将(22)式代入(13)式可得到

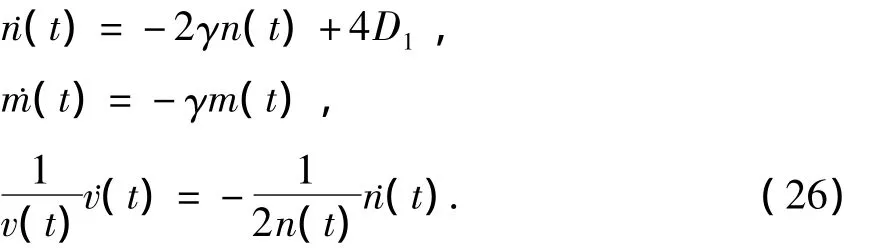
进一步求解方程(26)可得

将(22)，(23)以及(27)式代入(21)式可得

最后对(28)式求解可得信息熵表达式为［6－12］

3 耗散参数及非高斯噪声对系统信息熵的影响

下面我们分析系统耗散参数γ及非高斯噪声对系统信息熵的影响(所有计算值均为无量纲)．选取S(0)=0．0，n(0)=0．1．图1 我们给出了信息熵S随时间t的变化情况．从图1可见，S先是随着时间的增加而单调增加，但时间较大时，S最终趋向于一有限定值，系统的熵变化速度减缓，这表明系统内部各种因素的相互作用将最终使系统从非平衡态达到平衡态．图2我们给出了信息熵S随耗散参数γ的变化情况，从图2中可以看出，S随γ的增加而单调减小．图3我们给出了信息熵S随关联时间τ的变化．从图3中可以看出，S随关联时间τ的增加亦单调减少．图4我们给出了信息熵S随噪声强度D的变化情况，从图4中可以看出，S随噪声强度D的增加而单调增加．以上现象表明耗散参数γ与关联时间τ对系统信息熵的增加起到了抑制作用，即耗散参数γ与关联时间τ的增加有利于系统从非平衡态达到平衡态;而噪声强度D对系统信息熵的增加起到了促进作用，这使得系统从非平衡态达到平衡态的速度变缓．

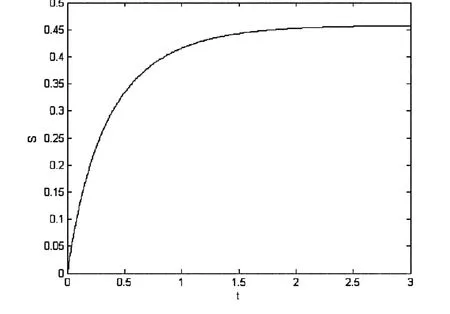
图1 信息熵S在D=0．5，γ=1．0，τ=2．0时随时间t的变化曲线Fig．1 Plot of S as a function of t at D=0．5，γ =1．0，τ=2．0

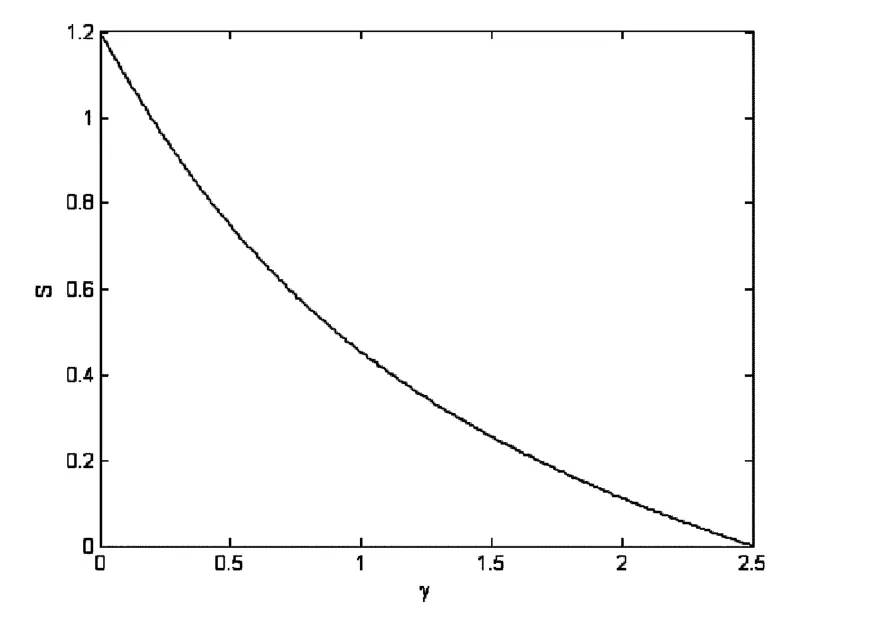
图2 信息熵 S 在 t=2．0，D=0．5，τ=2．0 时随耗散参数γ的变化曲线Fig．2 Plot of S as a function of γ at t=2．0，D=0．5，τ =2．0

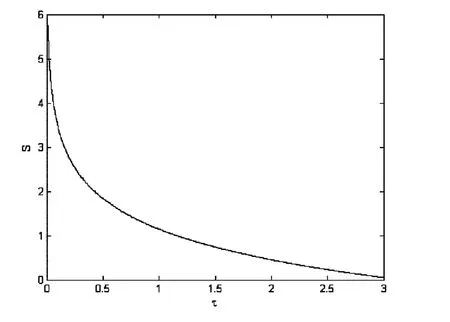
图3 信息熵 S 在 t=2．0，D=0．5，γ =1．0 时随关联时间τ的变化曲线Fig．3 Plot of S as a function of τ at t=2．0，D=0．5，γ =1．0

图4 信息熵S在t=2．0，γ=1．0，τ=2．0时随噪声强度D的变化曲线Fig．4 Plot of S as a function of D at t=2．0，γ =1．0，τ =2．0

4 结论

本文研究了一类由非高斯噪声驱动的耗散动力学系统的信息熵演化现象，文中首先通过路径积分法得到了系统的近似FPK方程，然后结合Shannon信息熵定义推导了该系统随时间演化的信息熵表达式．并进一步并分析了非高斯噪声及耗散参数对系统的信息熵演化的影响．通过数值计算发现，耗散参数γ与关联时间τ对系统信息熵的增加起到了抑制作用，而噪声强度D对系统信息熵的增加起到了促进作用．

1 Shannon C E．A mathematical theory of communication．Bell System Technical Journal，1948，27:379 ～423，623 ～656

2 Shannon C E．Communication in the presence of noise．Proceedings of the IRE，1949，37:10～21

3 邢修三．熵产生率公式及其应用．物理学报，2003，52(12):2969～2976(Xing X S．On the formula for entropy production rate．Acta Physics Sinica，2003，52(12):2969～2976(in Chinese))

4 邢修三．非平衡统计信息理论．物理学报，2004，53:2852 ～2863(Xing X S．Nonequilibrium statistical information theory．Acta Physics Sinica，2004，53:2852 ～2863(in Chinese))

5 Daems D，Nicolis G．Entropy production and phase space volume contraction．Physical Review E，1999，59:4000 ～4006

6 Bag B C，Chaudhuri J R，Ray D S，Chaos and information entropy production．Journal of Physics A:Mathematical and Genernal，2000，33:8331 ～8350

7 Bag B C，Banik S K，Ray D S．Noise properties of stochastic processes and entropy production．Physical Review E，2001，64，026110:1 ～7

8 Bag B C．Nonequilibrium stochastic processes:time dependence of entropy flux and entropy production．Physical Review E，2002，66，026122:1～12

9 Bag B C．Upper bound for the time derivative of entropy for nonequilibrium stochastic processes．Physical Review E，2002，65，046118:1 ～6

10 Goswami G，Mukherjee B，Bag B C．Coloured thermal noise－driven dynamical system:upper bound of time derivative of information entropy．Journal of Physics A:Mathematical and Genernal，2005，38:1659 ～1666

11 Goswami G，Mukherjee B，Bag B C．Colored thermal noise driven dynamical system in the presence and absence of non－equilibrium constraint:time dependence of information entropy flux and entropy production．Chemical Physics，2005，312:47 ～53

12 郭永峰，徐伟，李东喜等．准单色噪声驱动的耗散动力系统的信息熵演化．物理学报，2010，59:2235～2239(Guo Y F，Xu W，Li D X，et al．Time dependence of information entropy of a dynamical system driven by quasimonochromatic noise．Acta Physics Sinica，2010，59:2235～2239(in Chinese))

13 Xie W X，Xu W，Cai L．Time dependence of entropy flux and entropy production for a dynamical system driven by noises with coloured cross－correlation．Chinese Physics，2007，16:42 ～46

14 Xu W，Xie W X，Cai L，et al．Information entropy of a dynamical system driven by quasimonochromatic noise．Physica A，2007，384:273 ～277

15 Guo Y F，Xu W，Li D X，et al．Time dependence of entropy flux and entropy production of a dissipative dynamical system driven by non－Gaussian noise．Communications in Theoretical Physics，2008 49:1561 ～1566

16 Fuentes M A，Toral R，Wio H S．Enhancement of stochastic resonance:the role of non Gaussian noises．Physica A，2001，295:114 ～122

17 Fuentes M A，Wio H S．Toral R，Effective Markovian approximation for non－Gaussian noises:a path integral approach．Physica A，2002，303:91 ～104

18 Wio H S，Toral R．Effect of non－Gaussian noise sources in a noise－induced transition．Physica D，2004，193:161～168

19 Bouzat S，Wio H S．New aspects on current enhancement in Brownian motors driven by non－Gaussian noises．Physica A，2005，351:69～78

20 Wu D，Zhu S Q．Stochastic resonance in a bistable system with time－delayed feedback and non－Gaussian noise．Physics letters A，2007，363:202 ～212

21 Wu D，Luo X Q，Zhu S Q．Stochastic system with coupling between non－Gaussian and Gaussian noise terms．Physica A，2007，373:203 ～214

22 Kramers H A．Brownian motion in a field of force and the diffusion theory of chemical reactions．Physica，1940，7:284～304

23 Brody D，Meister B．An upper bound for entropy production．Physics Letters A，1995，204:93～98

*The project supported by the National Natural Science Foundation of China(11102132、11002110)

† Corresponding author E－mail:guoyongfeng@mail．nwpu．edu．cn

THE INFORMATION ENTROPY OF A DISSIPATIVE DYNAMICAL SYSTEM DRIVEN BY NON-GAUSSIAN NOISE*

Guo Yongfeng1†Zhao Xiaoshan2Tan Jianguo1
(1．School of Science，Tianjin Polytechnic University，Tianjin300387，China)(2．School of Science，Tianjin University of Technology and Education，Tianjin300222，China)

Entropy plays an important role in describing the evolution，instability，disorder or confusion and information transmission of stochastic systems．This paper investigated the time derivative of entropy for a dissipative dynamical system driven by non－Gaussian noise．The dimension of Fokker－Planck equation was reduced by the way of linear transformation．Based on the definition of Shannon＇s information entropy，the exact time dependence of the entropy was calculated．The relationship between the properties of non－Gaussian noise and dissipative parameters and their effect on the information entropy were also discussed．

information entropy， non－gaussian noise， dissipative dynamical system， Fokker－Planck equation

30 January 2013，

2 July 2013．

10．6052/1672－6553－2013－084

2013－01－30 收到第 1 稿，2013－07－02 收到修改稿．

*国家自然科学基金资助项目(11102132、11002110)

E－mail:guoyongfeng@mail．nwpu．edu．cn