自适应多尺度熵在脑死亡诊断中的应用*

倪力 曹建庭 王如彬†

(1．华东理工大学认知神经动力研究所，上海 200237)(2．日本琦玉工业大学大学院工学研究科，日本琦玉县深谷市 396－0293)(3．日本理化研究所脑科学研究中心，日本琦玉县和光市 351－0198)

自适应多尺度熵在脑死亡诊断中的应用*

倪力1曹建庭2，3王如彬1†

(1．华东理工大学认知神经动力研究所，上海 200237)(2．日本琦玉工业大学大学院工学研究科，日本琦玉县深谷市 396－0293)(3．日本理化研究所脑科学研究中心，日本琦玉县和光市 351－0198)

本文引入自适应多尺度熵的方法，并结合当前常用的经验模型分解的方法，使得数据尺度能自适应的被获取．通过从原数据中不断移除低频或高频成分，自适应多尺度熵能够在“从粗糙到精细”或是“从精细到粗糙”的尺度下用样本熵估计求得．模拟结果用来确认了其有效性，同时我们将其应用到脑死亡诊断中，用来区分脑死亡病人和昏迷病人在脑电信号上的不同．

脑电信号， 脑死亡诊断， 自适应多尺度熵， 样本熵

引言

脑死亡的定义是完全的、不可逆和永久的脑和脑干功能丧失，但即便是在这样定义下，由于一些临床的因素，我们很难对于脑死亡的判定精确实施．传统的临床测试在一些场合下代价昂贵、花费时间过长，甚至会引起危险(如自主呼吸测试)．为了避免这样的缺点，我们提出了脑电预检测流程，并将其安插在自主呼吸之前，这将会使整个脑死亡测试更为简单有效并降低风险，如此还能帮助医生判断是否有继续进行脑死亡测试的必要［1］．为了确认伪脑死状态，我们将采用脑电图仪这种为人们所熟知的临床工具来观测脑信号，而事实上，已经有许多国家已经采用了这样的方法来评估脑皮层的功能缺失［1］，［2］．我们的研究目的就是提供一个基于脑电分析的数学计算方法来为脑死亡诊断提供一个清晰的标准，同时帮助临床医生来具体实施．

非线性生理系统的复杂度已在世界范围内在健康和病态的区别中被广泛研究．一个生理时间序列所携含的复杂度信息往往直接反映了生理系统的状态［3］．近似熵和样本熵在复杂度分析中是切实有效的，给予我们一个更好的视角来理解生物系统．Pincus首先引入了近似熵(Approximate Entropy，ApEn)的方法，并且在分析心电和其他一些时间序列中表现出色［4］．Richman和Moorman在此基础上开发了样本熵(Sample Entropy，SampEn)算法，相比之下，解决了近似熵会因计算过程中的“自我比较”引起偏差的问题［5］．Costa引入了多尺度的计算方法，同时将之结合样本熵计算—将多尺度特性也纳入了考虑［6］．多尺度的方法在对于原数据进行线性平滑的过程中不可避免的丢失了重要信息，此外在尺度提取方面不能很好地适应非线性和非平稳的信号．

为了解决上述问题，我们提出了自适应多尺度熵的方法来分析数据．不同于标准的多尺度方法，我们通过经验模型分解(Empirical Mode Decomposition，EMD)从数据中分离出本征模态函数(Intrinsic Mode Function，IMF)来确定计算所使用的尺度;经验模型分解是一个完全由数据驱动的时频技术，用来自适应地将一个信号分解成数个调制成分—本征模态函数．本征模态函数代表着一种单一的振荡形式，并具有良好的性质．于是我们可以不断从原数据中移除低频或是高频成分，并定义“从粗糙到精细”或是“从精细到粗糙”这两个过程来通过样本熵的方法来计算其数据的复杂度的变化［7］［8］．我们希望通过此方法来探究昏迷病人和脑死亡病人在脑电分析中的复杂度和能量不同，并希望能够进一步将实验数据与计算神经科学结合来完善这方面的工作［9～11］．

此文中，我们首先介绍样本熵的计算方法和经验模型分解的计算流程;然后结合并运用上述两种方法，提出了我们的自适应多尺度熵的方法，并用来计算所采集的脑电数据．最后是结论和讨论．

1 脑电数据分析方法

1．1 样本熵

对于样本熵的的计算方法中，对于一个有限的长度为N的时间序列U=［u1，u2，…，uN］，按顺序构造出m维矢量Xi=［ui，ui+1，…，ui+m－1］和Xj=［uj，uj+2，…，uj+m－1］，其中i，j≤N－m+1．计算出Xi和Xj的距离．

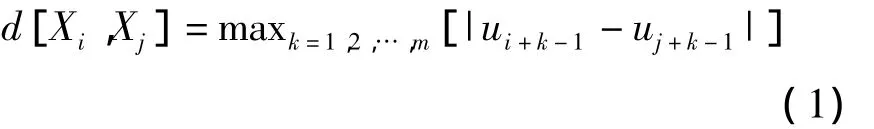
令表示为Xi和Xj距离在r以内的数目乘上(N－m)－1，其中1≤j≤N－m+1，i≠j．

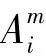
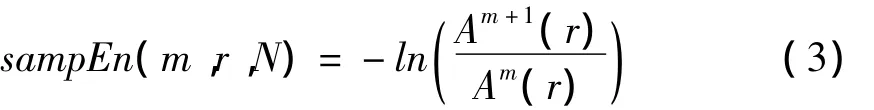
1．2 多尺度分析

用多尺度样本熵(Multiscale entropy，MSE)的手段来分析脑电信号内固有的复杂度变化是十分有必要的，而这种思想也首先由 Costa提出［6］．我们认为在不同尺度下的动力学系统的复杂度会揭示出其结构的不同，而此类特征可以帮助我们很好的解决问题．

给定一个长度为N的一维的离散时间序列U=［u1，u2，…，uN］，将其分成长度为 epsilon 的不重叠的时间窗口，并将时间窗口内的数据取平均值，由此，我们可以得到一个“粗糙化”的新时间序列

通过将维数增加到m+1，重复式(1)(2)中的步骤，我们可以得到Am+1．样本熵的表达式为

式中1≤j≤N/∈．对于重构的尺度为∈的新时间序列，计算出其相应的样本熵的值并且绘制出样本熵关于尺度的函数．经过这样的处理，所得数据便是原数据的1/epsilon了，当然当∈=1时，数据长度保持不变．

1．3 经验模型分解

经验模型分解是完全由数据驱动的方法，它将一个时间序列分解成一系列基于尺度独立的本征模态函数集，从而表征了数据的内在振荡形式．

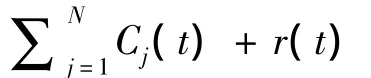
1．4 自适应多尺度熵

我们提出的自适应多尺度熵(Adaptive Multiscale Entropy，AME)主要包含了两个步骤:1)通过经验模型分解在各个尺度上将数据分解成一系列本征模态函数;2)在所选定的尺度上，计算其样本熵的值．而每个尺度是由不断移除低频或高频成分的过程决定的．此过程定义了“从粗糙到精细(c2f)”或是“从精细到粗糙(f2c)”这两个算法(高通或是低通)．

算法1:“从精细到粗糙”自适应多尺度熵

1)通过经验模型分解获得本征模态函数．

2)从原数据中从第一个本征模态函数开始开始连续移除高频的本征模态函数，

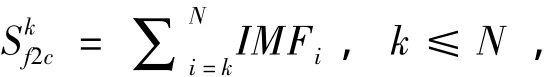
3)自适应多尺度熵是在每一个尺度上计算其样本熵的值来获取每一个独立尺度上的熵，

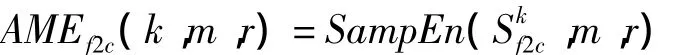
算法2:“从粗糙到精细”自适应多尺度熵

1)通过经验模型分解获得本征模态函数．

2)从原数据中从第一个本征模态函数开始开始连续移除低频的本征模态函数，

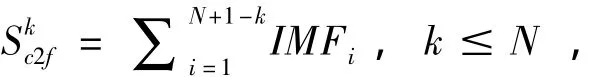
3)自适应多尺度熵是在每一个尺度上计算其样本熵的值来获取每一个独立尺度上的熵，

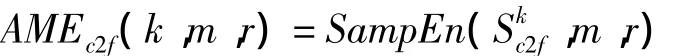
2 实验结果

2．1 实验环境

在我们目前的研究中，脑电实验是在医院的重症监护室中进行的．在脑电数据记录中，我们将7个电极放置在病人的前额．其中6个通道与之相对应电极(Fp1，Fp2，F3，F4，F7，F8)连接;另一通道GND接地，其采样频率均为1000赫兹．

2．2 样本熵的结果

首先让我们来关注一下下面的表格，其中分别记录了昏迷病人(C)脑死病人(D)的近似熵和样本熵在不同阈值和通道的实验结果．通常我们采样100－5000个数据点，置m=2，阈值为r×SD．

表1 令 r=0．15×SD，在这个阈值下计算每一个通道间的差值d=0．97Table 1 Set r=0．15 ×SD，with this threshold，calculate the average difference d=0．97

表2 各个通道在阈值r=0．15×SD下同一病人在昏迷和脑死亡状态下样本熵的差值d=1．48Table 2 Sample entropy results of a certain patient in the state of coma(C)and brain death(D)for each channel with threshold r=0．15 × SD，d=1．48

从表1中我们可以看出样本熵的值能显著的区分昏迷病人和闹死病人．此外，计算脑死病人和昏迷病人间的差值，不难发现，尤其在阈值为r=0．15×SD的样本熵案例中，相较之其他情况两状态的界线尤为清晰．总之，我们以样本熵的计算作为我们研究的首选．同时为了消除这种差异是由不同的病人引起的，我们在表2中另举一例以进一步证实我们的观点．

显然，对于同一个人的不同状态，其样本熵的值依然是有巨大差异的，这意味着样本熵的方法可以有效的帮助我们来进行脑死亡诊断．

但是，为了严谨的对待脑死亡诊断，我们需要更为可靠的数学工具来提高我们计算的可靠性．单纯使用样本熵虽然在一定程度上已经能很好的区分这两种状态，但是我们在多次计算和使用中也会发现一些不尽人意的结果．于是我们提出了自适应多尺度熵的方法来帮助我们提高计算的准确性，降低临床操作中带来的风险．

2．3 自适应多尺度熵的结果

通过经验模型分解我们对与所采集的的所有数据的任一时间段进行运算，将其分解成一系列本征模态函数．于是这样我们可以根据已经定义的两个过程，在每一个尺度上计算时间序列的样本熵的值．我们希望通过在不同的时间尺度上找到一些显著的特征来帮助我们区分昏迷病人和脑死亡病人．

如图1所示，我们对总计60段脑电数据进行多尺度计算，对于昏迷病人的脑电数据的样本熵的值，其通常能够分解6～7个成分(包括残余)，在不断移除高频成分的过程中，其样本熵的值呈单调递减的趋势，不难解释这是由于随着高频成分的减少，时间序列呈显更强的规律性和自相似性，所以复杂度降低，样本熵的值也会随之降低;相比较之下，闹死病人的脑电数据(由环境噪声构成)也呈现同样的单调递减性，但是其在前4个尺度下的样本熵的值均高于昏迷病人，这说明对于一段主要由噪声构成的脑电数据，其复杂度要远高于具有节律性的脑活动的昏迷病人，在实验中我们也发现对于脑死亡病人脑电数据通常能够分解成7～8个成分，较之昏迷病人，其成分更为复杂．

在此粗糙化的过程中，最大的差距依然发生在尺度1的地方，两种状态的差距随着尺度的增加而减小．即使是这样，我们可以确保在每一个尺度均有样本熵的数值的巨大差距来增加我们实验的准确率和可行性．

紧接着我们进行了精细化计算，即从脑电数据中不断移除低频成分，其结果如图2所示．在此过程中两种状态下的曲线均呈现出先递增后递减的形状，当我们移除前几个低频成分时，脑电数据的复杂度增加，当继续移除以至于成分越来越少时，数据复杂度自然就降低了，所以有上述的形状．同样的，几乎在每一个尺度上脑死亡病人的样本熵值均明显高于昏迷病人的．此外，两者间最明显的差距发生在尺度2，而不是原数据处．这为我们区分昏迷病人和脑死亡病人的脑电提供了宝贵的参考．

作为比较我们同样提供多尺度熵的计算结果，如图3所示．我们取了100个尺度进行粗糙话处理，在每一个尺度上计算样本熵的值．我们可以发现在低尺度上差距依然是巨大的，昏迷病人的曲线呈现出单调递增而反之脑死亡病人的却是单调递减，产生的一个问题是，随着尺度的增加，两者数值会发生翻转，这可能会对我们的判断造成困惑．

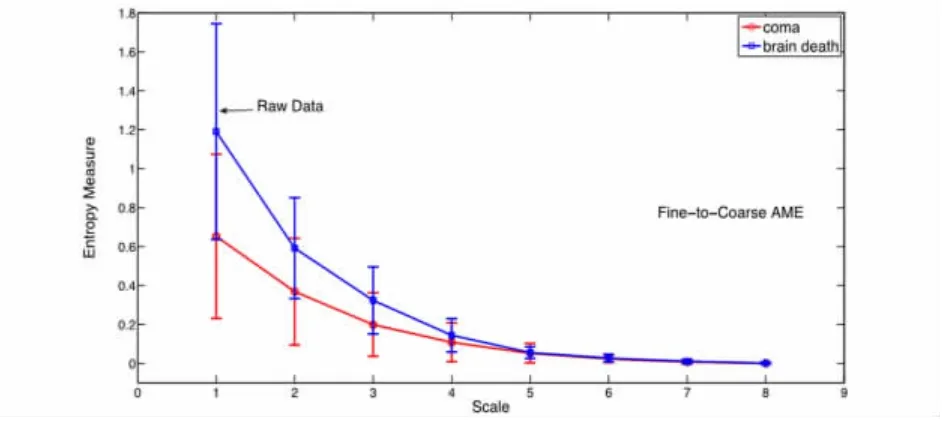
图1 对于所有样本的从精细到粗糙自适应多尺度熵的分析，比较昏迷状态(红色圆圈)与脑死亡状态(蓝色方块)．最大的差距发生在尺度1处(原数据)Fig．1 Fine－to－Coarse AME results for all samples，coma(red circle)versus brain death(blue square)．The most significant differences occur at the first scale(raw data)

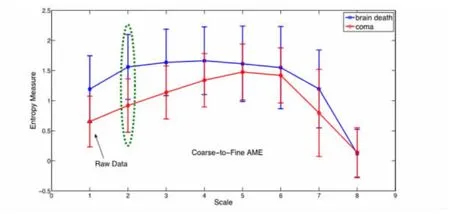
图2 对于所有样本的从粗糙到精细自适应多尺度熵的分析，比较昏迷状态(红色圆圈)与脑死亡状态(蓝色方块)．最大的差距发生在尺度2处，由绿色椭圆标注Fig．2 Coarse－to－Fine AME results for all samples，coma(red circle)versus brain death(blue square)．The most significant differences occur at the second scale marked by green ellipse

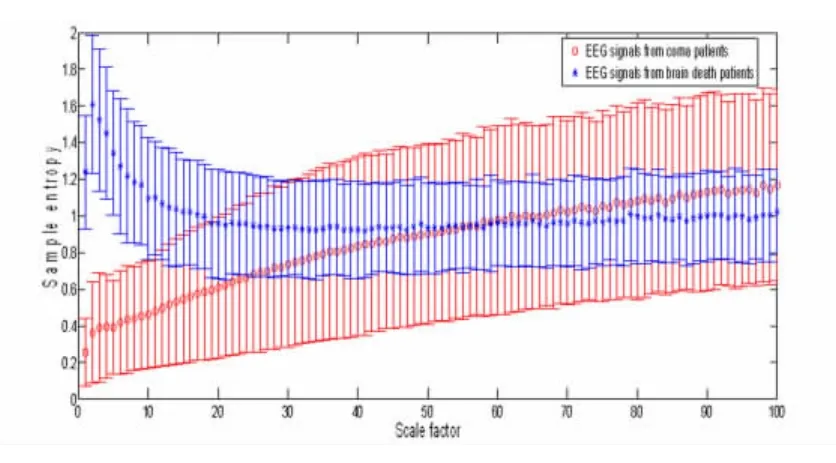
图3 对于所有样本的多尺度熵的分析，比较昏迷状态(红色圆圈)和脑死亡病人(蓝色星号)Fig．3 MSE results for all samples，coma(red circle)versus brain death(blue asterisk)

3 结论

本文提出了基于经验模型分解的自适应多尺度熵的方法，并运用样本熵在每一个尺度上计算其复杂度．将所采集的脑电数据分解成的一系列独立尺度的本征模态函数，将其从原数据中移除，从而定义了粗糙化和精细化的这两个过程，并结合脑死亡诊断，在计算数值上十分明显的区别，证明了此方法的有效性和可行性，并且能够为其他的数据比较提供思路．对于我们实验中的非线性、非平稳的脑电信号处理中，我们得到了如下结论:

(1)对于脑死亡病人的脑电数据的复杂度在每一个尺度上均高于昏迷病人的脑电数据，说明昏迷病人存在节律性脑电活动，其复杂度较低．

(2)对于两种状态的比较，在粗糙化过程中，最大差距发生在尺度1处;在精细化过程中，最大差距发生在尺度2处．尺度的选择会提高我们脑死亡诊断的准确性．

(3)两种状态的脑电数据成分数量也不同，昏迷病人的成分较之脑死亡病人会比较少，也是从一个侧面证明了其复杂度较低，具有节律性脑活动．

1 Cao J，Chen Z．Advanced EEG signal processing in brain death diagnosis．In:Signal Processing Techniques for Knowledge Extraction and Information Fusion．2008，275～297

2 Eelco F，Wijdicks M．Brain death worldwide．Neurology，2002，58:20～25

3 Taylor R M．Reexaming the definition and criteria of death．Seminars in Neurology，1997，17:265～270

4 Pincus S M．Approximate entropy as a measure of system complexity ．Proceedings of the National Academy of Sciences of the United States of America．1991，88(6):2297～2301

5 Richman J S，Moorman J R．Physiological time－series analysis using approximate entropy and sample entropy．AJP－Heart and Circulatory Physiology，2000，278(6):2039～2049

6 Costa M，Goldberger A L，Peng C －K．Multiscale entropy analysis of complex physiologic time series．Physical Review Letters，2002，89(6):68～102

7 Hu M，Liang H．Intrinsic mode entropy based on multivariate empirical mode decomposition and its application to neural data analysis．Cognitive Neurodynamics，2011，5(3):277～284

8 Hu M，Liang H．Adaptive multiscale entropy analysis of multivariate neural data．IEEE Transactions on Biomedical Engineering，2011，59(1):12 ～15

9 汪雷，刘深泉．皮层锥体神经元模型的动力学分析．动力学与控制学报，2011，9(1):49～53(Wang L，Liu S Q．Dynamical analysis of cortical pyramidal neuron model．Journal of Dynamics and Control，2011，9(1):49 ～53(in Chinese))

10 王海侠，陆启韶，郑艳红．神经元模型的复杂动力学:分岔与编码．动力学与控制学报，2009，7(4):293～296(Wang H X，Lu Q S，Zheng Y H．Complex dynamics of the neuronal model:bifurcation and encoding．Journal of Dynamics and Control，2009，7(4):293 ～ 296(in Chinese))

11 王如彬，张志康，沈恩华．大脑皮层内神经元集团的能量演变．动力学与控制学报，2008，6(1):55～60(Wang R B，Zhang Z K，Shen E H．Energy evolution of neural population in cerebral cortex．Journal of Dynamics and Control，2008，6(1):55 ～60(in Chinese))

*The project supported by the National Natural Science Foundation of China(11232005)，Research Fund for the Doctoral Program of Higher Education of China(20120074110020)

† Corresponding author E－mail:rbwang@163．com

BRAIN DEATH DIAGNOSIS BASED ON ADAPTIVE MULTI-SCALE ENTROPY ANALYSIS*

Ni Li1Cao Jianting2，3Wang Rubin1†
(1．Institute for Cognitive Neurodynamics，East China University of Science and Technology，Shanghai200237，China)(2．Saitama Institute of Technology1690Fusaiji，Fukaya-shi，Saitama369-0293，Japan)(3．Brain Science Institute，RIKEN2-1Hirosawa，Wako-shi，Saitama351-0198，Japan)

This paper introduced the adaptive multi－scale entropy(AME)measures，in which the scales are adaptively derived from the data by virtue of recently developed empirical mode decomposition．By removing the low or high frequency components from the raw data，the AME can be estimated at either coarse－to－fine or fine－tocoarse scales，over which the sample entropy is performed．Simulations illustrate its effectiveness and promising application in brain death diagnosis to discern the states of the coma and the brain death．

EEG signal， brain death diagnosis， adaptive multi－scale entropy， sample entropy

8 June 2013，

16 June 2013．

10．6052/1672－6553－2013－086

2013－06－08 收到第 1 稿，2013－06－16 收到修改稿．

*国家自然科学基金资助项目(11232005)，教育部博士点基金资助项目(20120074110020)

E－mail:rbwang@163．com