简支梁移动质量响应分析*

郭树起 孔艳平 杨绍普

(1．石家庄铁道大学工程力学系，石家庄 050043)(2．石家庄铁道大学机械学院，石家庄 050043)

简支梁移动质量响应分析*

郭树起1†孔艳平1杨绍普2

(1．石家庄铁道大学工程力学系，石家庄 050043)(2．石家庄铁道大学机械学院，石家庄 050043)

随着行车速度与交通量不断增加，荷载不断加重，桥梁的移动荷载响应越来越得到人们的重视．考虑移动车辆的惯性效应与桥梁的阻尼效应时，需要把车辆荷载简化为移动质量进行研究，这时得到的控制方程是变系数偏微分方程，在数学上通常难以精确求解．经分离变量与模态叠加后，化为变系数常微分方程组．本文利用WKB法，得到了近似的动力学响应，并与数值解、移动常力、Inglis解进行了比较．

简支梁， 移动质量， WKB法

引言

随着行车速度的不断提高，交通密度的不断增加，荷载的不断的加重，移动荷载与结构的动力相互作用问题越来越得到人们的重视．常见的移动荷载模型有移动力、移动质量和移动车辆．移动荷载与均匀的各向同性的材料及其结构的耦合动力学的研究有很长的历史和很多文献．Flyba的专著汇集了前人的工作，进行了系统的理论分析研究，对近后续学术研究产生了巨大的影响［1－2］．我国科学工作者也走在本领域的前列，著名学者有:北京交通大学的夏禾，东南大学的邓学钧和孙璐［3］，铁道科学研究院的潘家英和高芒芒［4］，同济大学李国豪院士［5］，台湾的杨永斌教授［6］．还有西北大学的宋一凡教授［7］，西南交通大学的翟婉明教授［8］，郑州的李广慧在无碴轨道轨道方面的工作［9］，湖南大学的陈政清［10］，均在在本领域做了大量的工作并有专著出版．这些专著中引用了大量的文献，评述了本领域学术发展概况．

文献中对于移动常力的情况进行了详尽的研究，但对于移动质量、移动车辆等更复杂的情形，由于问题的复杂性，通常采用数值仿真的方法．本文则利用改进的WKB［11－12］法，得出了此问题的近似解，并与移动常力解、Inglis解、数值仿真进行了比较．分析计算表明，本文得到的解析解具有更高的精度，精度明显高于Inglis解、移动常力解．

1 控制方程

当有移动质量存在时，欧拉-伯努利梁的控制方程为

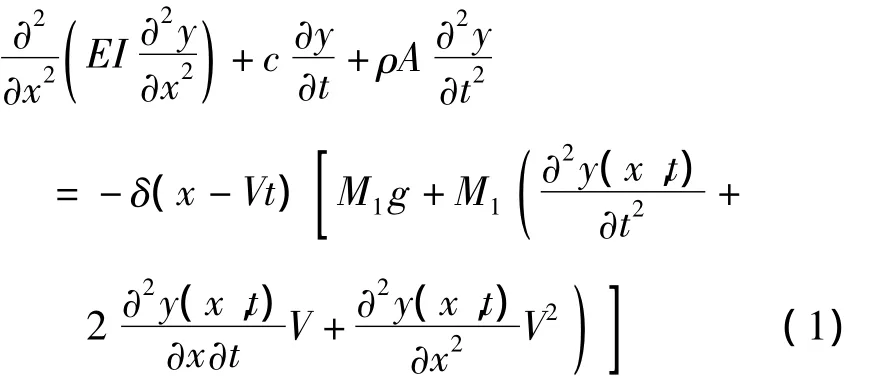
其中移动质量M1以匀速V在梁上通过，式中圆括号内第一项表示车辆所在位置桥梁振动的竖向加速度，后面两项对桥梁的阻尼与刚度有所影响，一般可以忽略不计［12］．因此考虑移动荷载的质量的简支梁动力平衡方程简化为

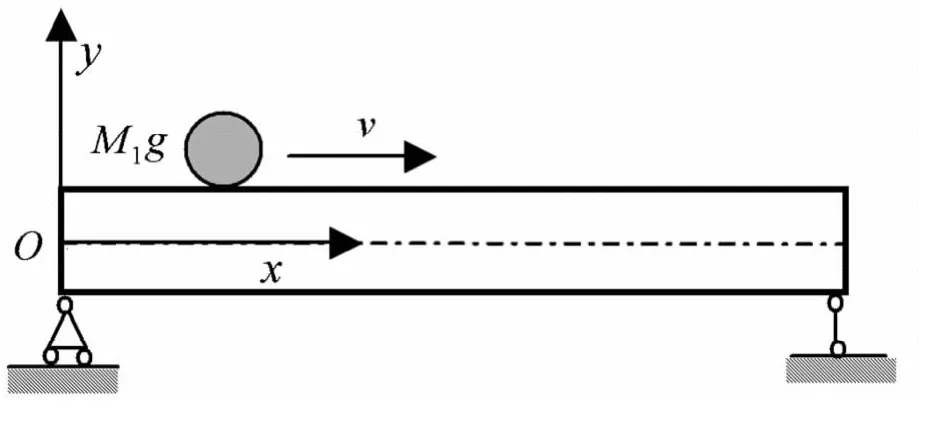
图1 简支梁上移动质量示意图Fig．1 The schematic diagram of simple supported beam under the moving mass

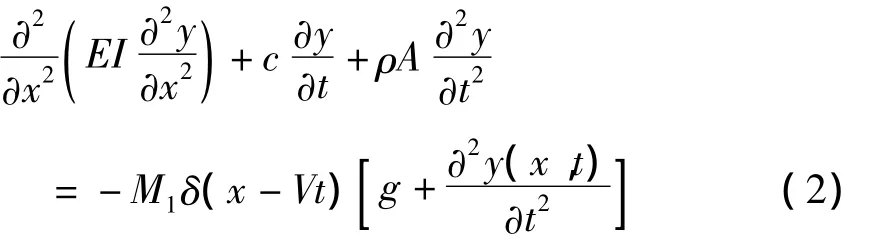
对简支梁按照振型分解，即

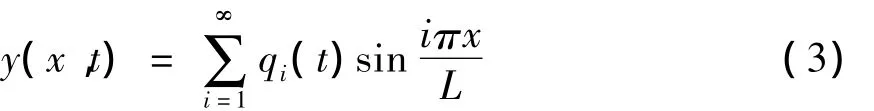
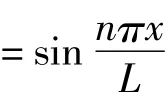
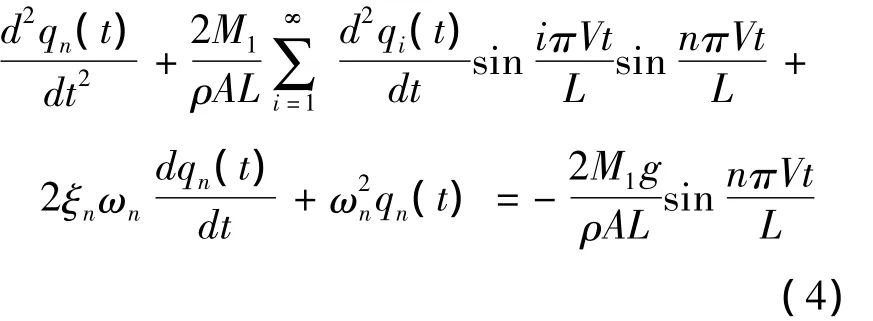
由于有无穷个变量，而且互不独立，难于解析求解．在此采用改进的WKB法［12－13］求解此方程的近似解．由于式(4)各个模态之间耦合．难以求得解析解．因此转而求近似解．略去除耦合项，即略去质量矩阵的非主对角线元素，此时式(4)变为

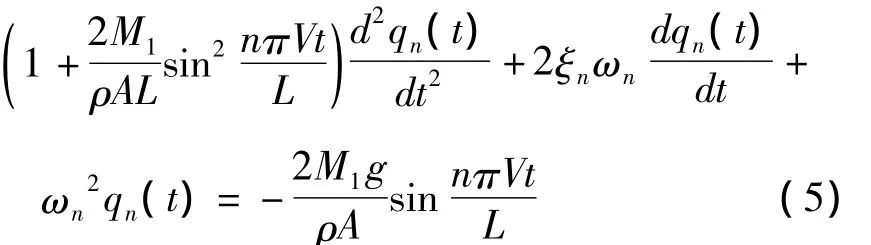
一般来说，考虑第一阶模态就有很好的精度，即使对于移动常力的情况，通常也只取第一阶模态．这时不存在模态耦合问题，式(4)与式(5)相同．

首先无量纲化，令

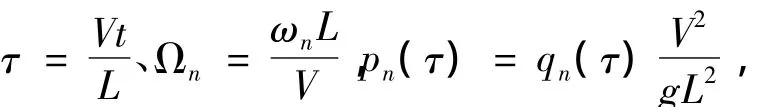
则式(5)变为

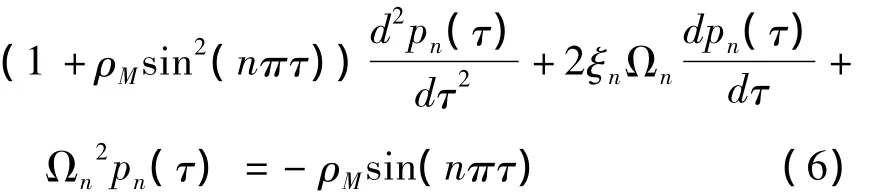
我们首先考虑无阻尼的情形．

2 无阻尼情形

若阻尼等于零，即ξ=0，控制方程化为

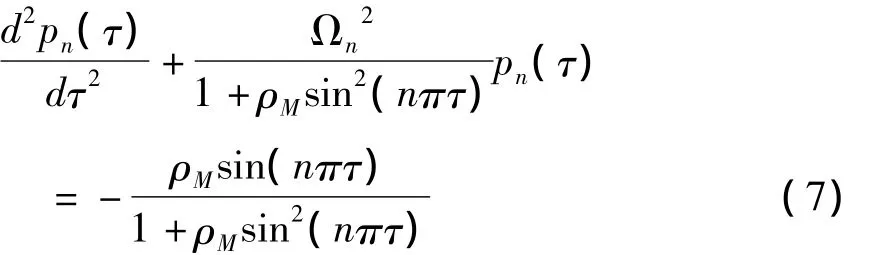
根据改进的WKB法，取其次方程的一阶近似解

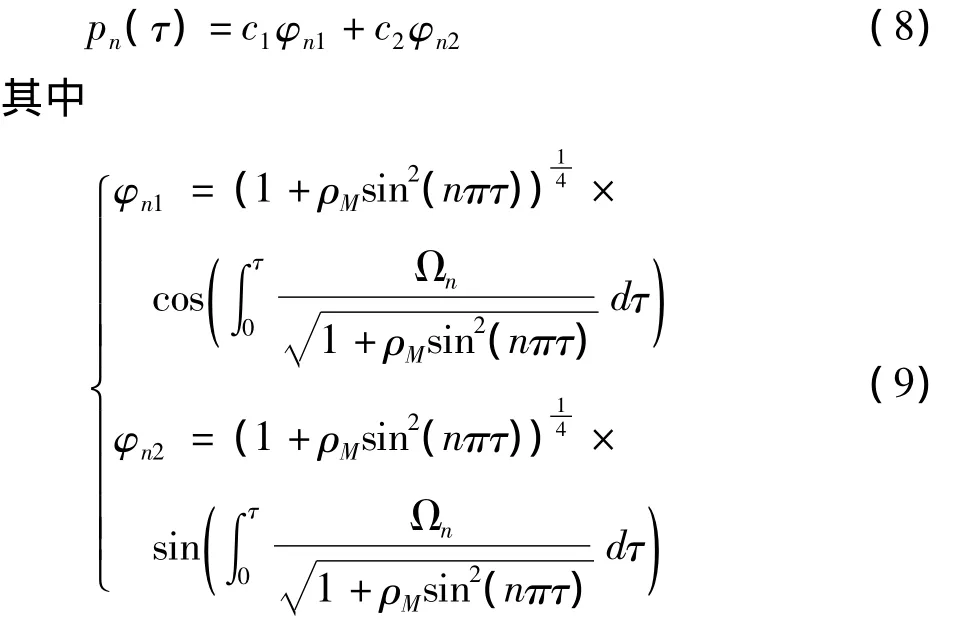
则根据常数变易法可以得到自由振动解为

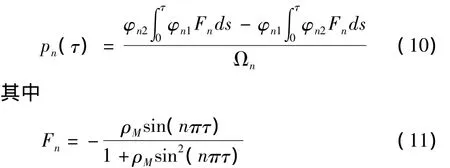
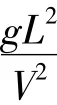
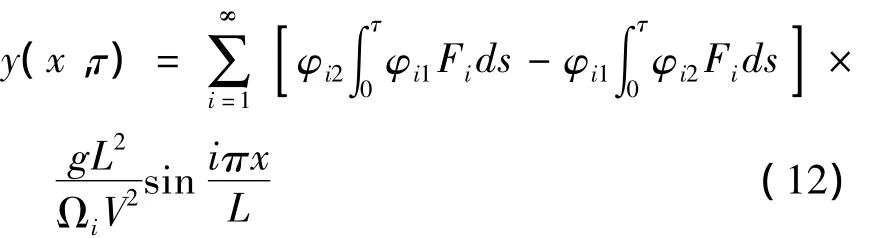
其中φi1与φi2如式(9)所示．实际中一般取一阶模态，即

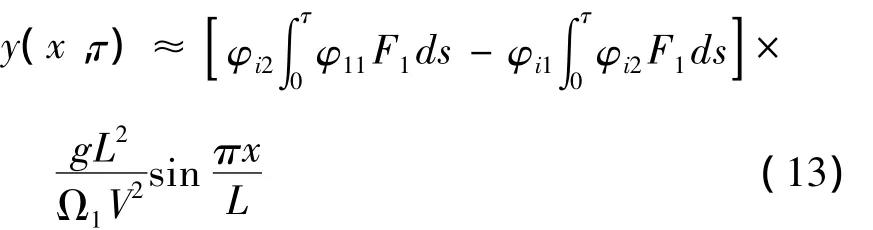
可见随着ρM的增加，挠度也跟着增加．随着无量纲Ω值的减弱，挠度也迅速增加．从Ω的定义可以知道，移动质量的行走速度增加可以减弱Ω的值，对于式(13)，仍难以写为简单函数的表达式．对于ρM＜1的情形，我们可以式(10，12)中的积分进行对ρM泰勒展开为收敛级数．当ρM＞1时，泰勒展开的级数收敛性难以判定．注意到

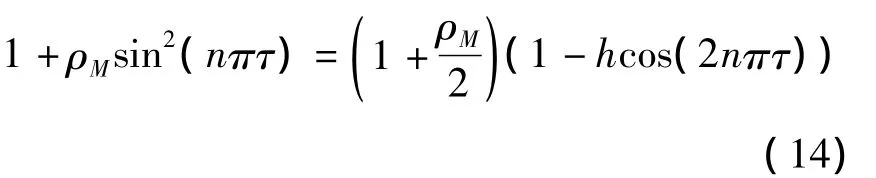
其中h是新的常数，定义为

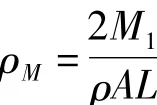
参数h表示了移动质量与系统总质量的比值，其范围在0与1之间变化．φn1、φn2、Fn与pn均可用此参数展开．但是由于系统的解与ρM成正比，因此Fn分子上的ρM不必用h展开．这样可以假设pn(τ)的形势如下

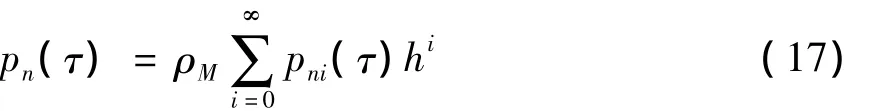
通常只需要计算第一阶模态所对应的p1(τ)

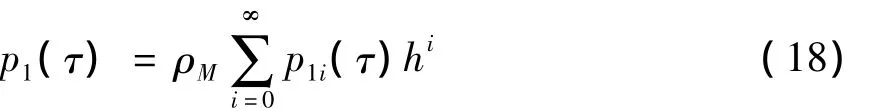
随着阶数的增高，pni的表达式变得复杂．数值解表明，计算前第一阶振型的前3项即可．经过计算得到式(17)中的pn0(τ)、pn1(τ)与pn2(τ)计算结果如下

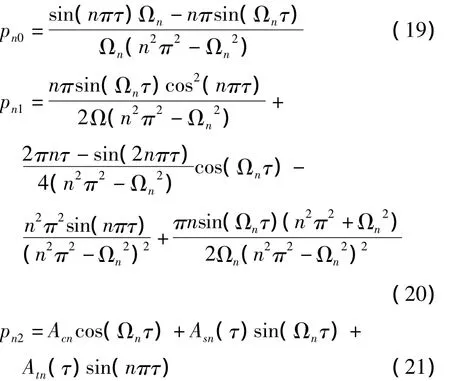
其中Acn、Asn与Atn如式(22 ～24)所示

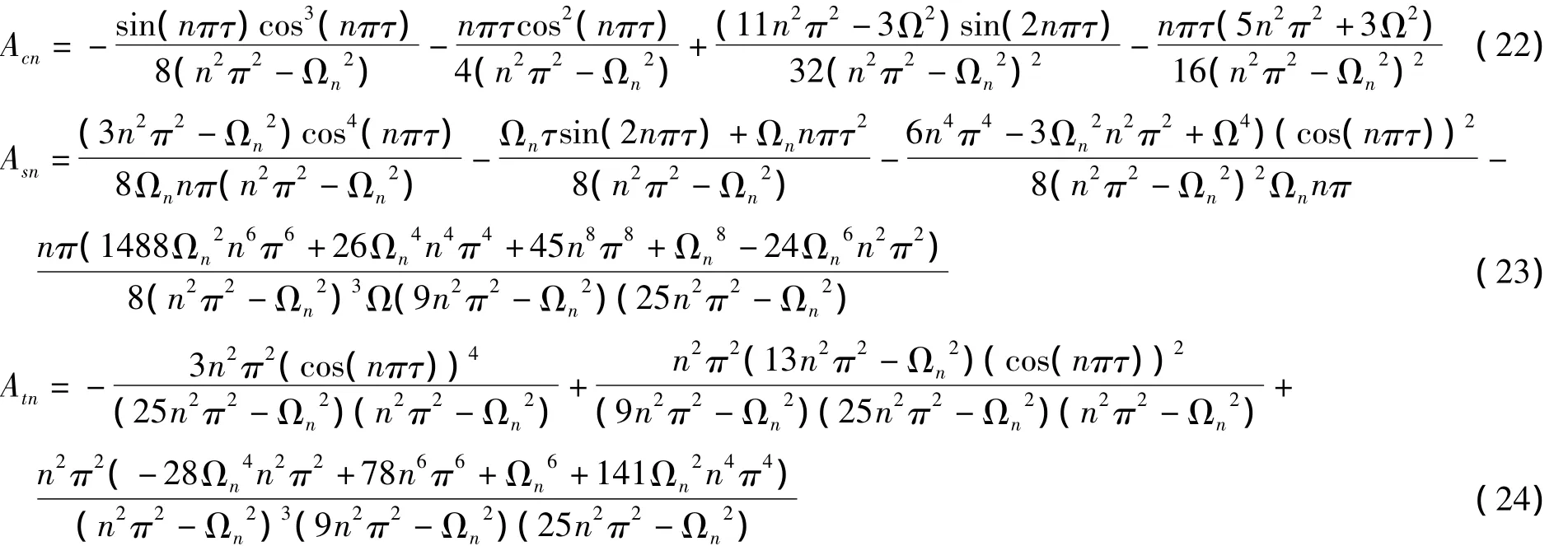
当n=1时化为式(18)中的系数．显然当h为0，则上述解化为移动常力的解．取式(18)中取前三项，简支梁的移动质量响应可以近似表达为

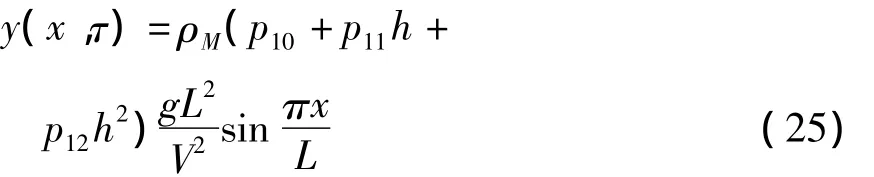
3 WKB解、移动常力解、Inglis解与数值解比较

将h=0带入式(31)得到移动常力的第一阶振动表达式

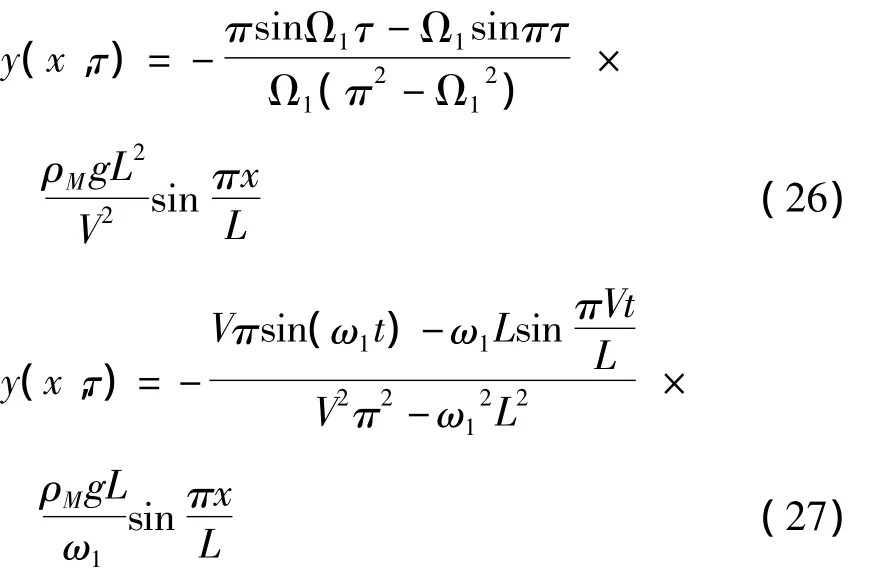
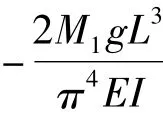
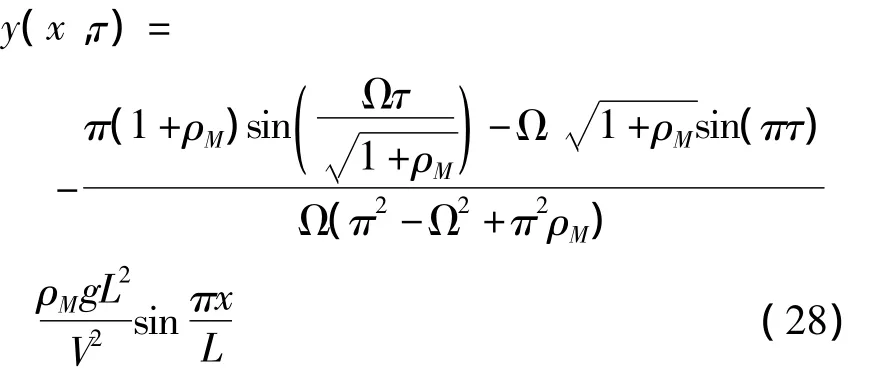
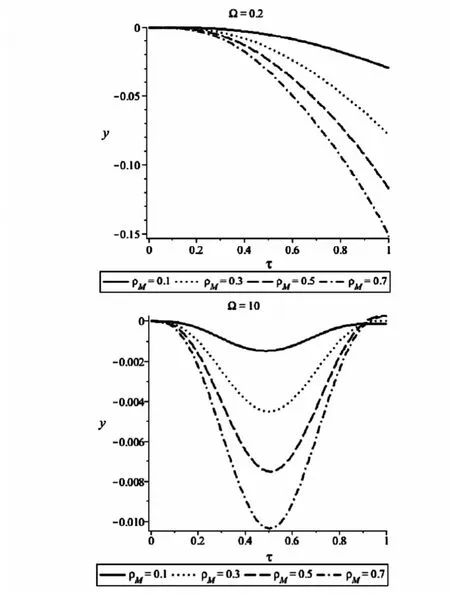
图2 不同ρ值的简支梁跨中挠度曲线Fig．2 The deflection curve of simple supported beam at midspan with different value of ρ

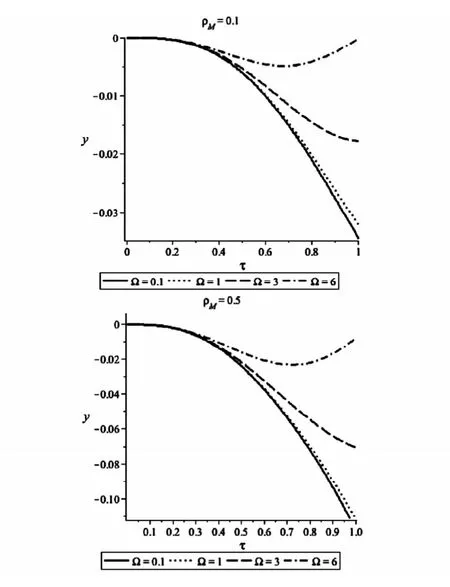
图3 不同Ω值的简支梁跨中挠度曲线Fig．3 The deflection curve of simple supported beam at midspan with different value of Ω

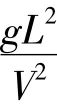
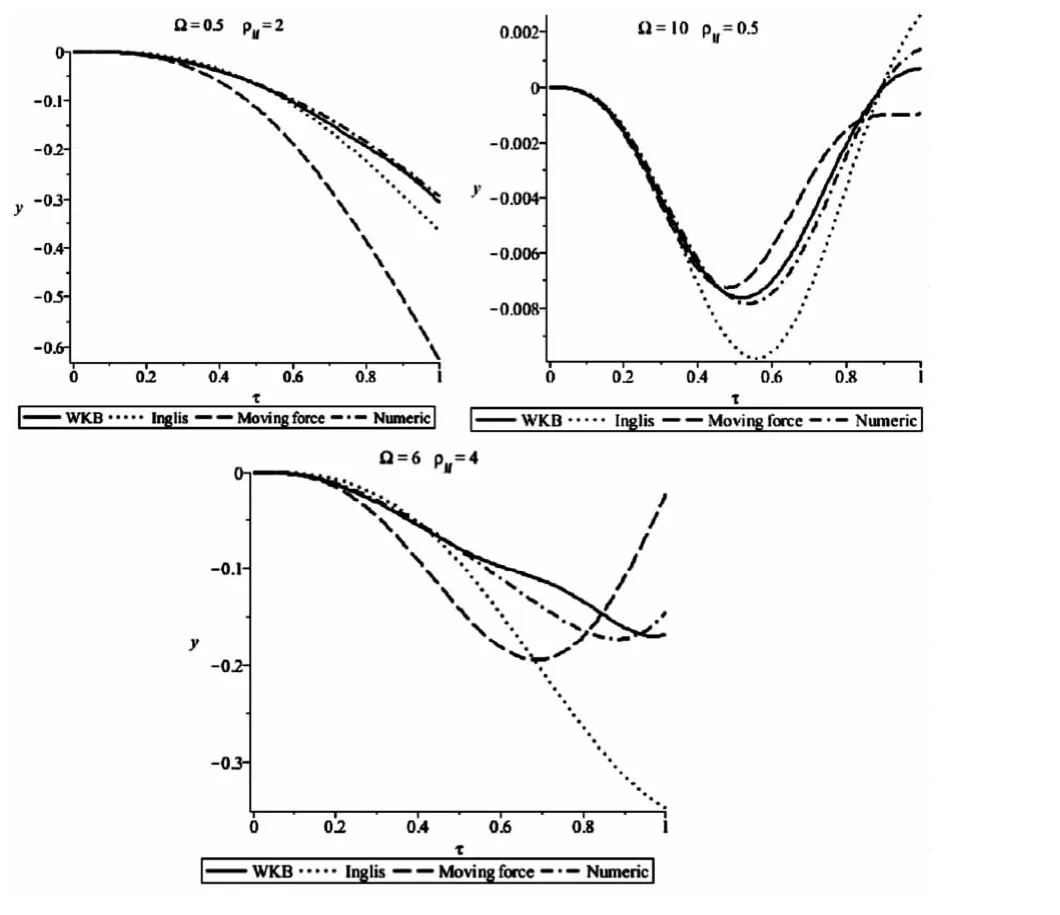
图4 WKB解、Inglis解、移动常力解与数值解比较Fig．4 The deflection curve of simple supported beam at midspan for four solutions

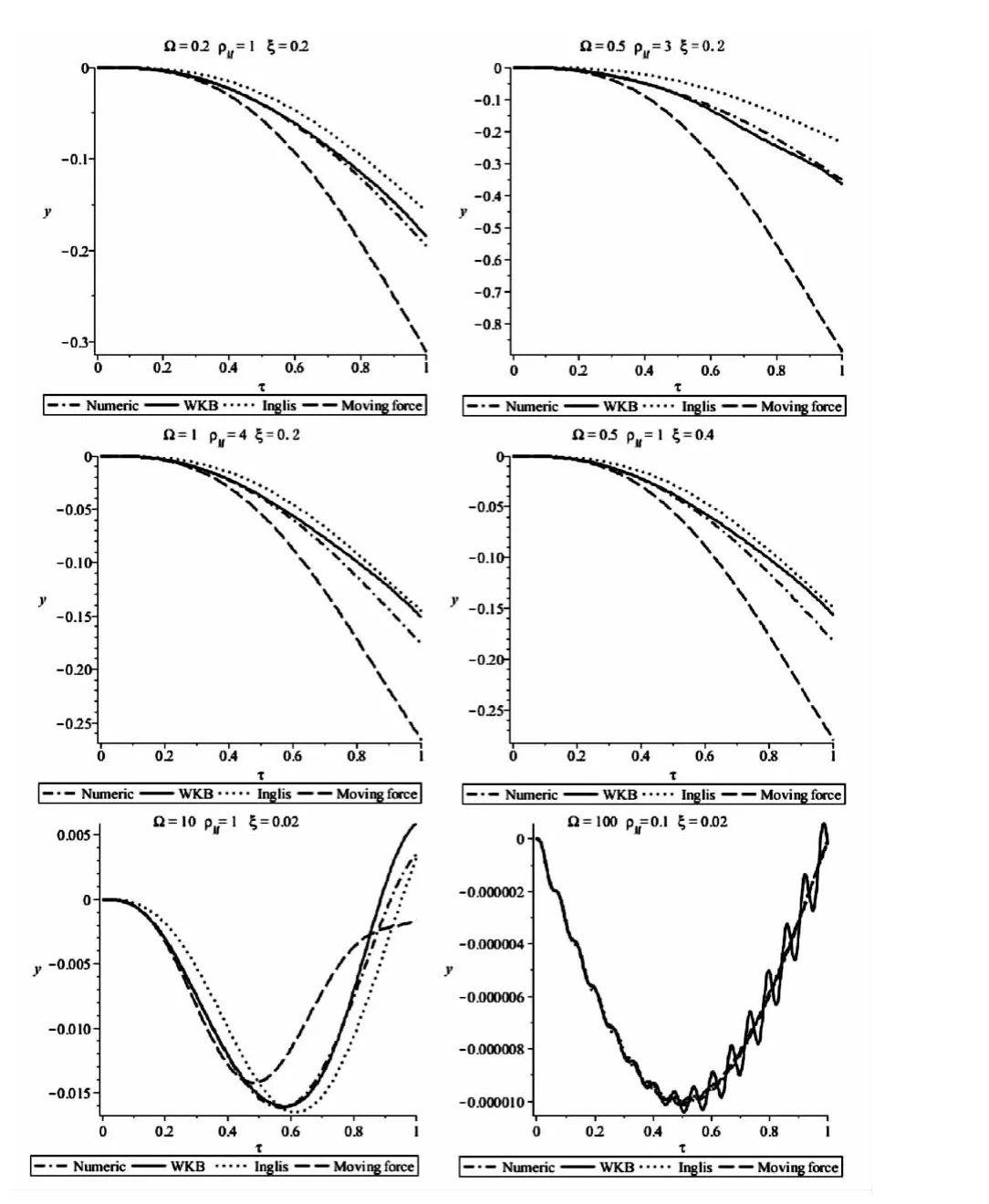
图5 阻尼存在时WKB解、Inglis解、移动常力解与数值解比较Fig．5 The deflection curve of simple supported beam at midspan for four solutions with damping

4 有阻尼时的情形

此时这样pn(τ)就在无阻尼解的基础上再加上阻尼的影响．设不考虑移动物体的惯性影响时，相应的解为 ρMDn(ξn，τ)，且容易求出．计算表明，当阻尼为零时，ρMDn(ξn，τ)化为移动常力的解．那么在上两节解的基础上叠加ρMDn(ξn，τ)可以得到有阻尼时的近似解．即此时有第n阶pn(τ)的一般表达式可以假设设为

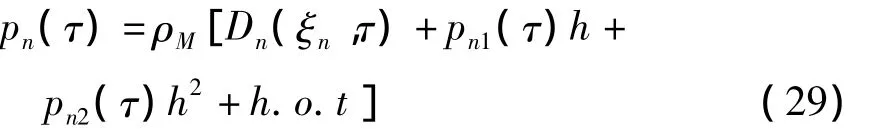
通常只需要计算第一阶模态p1(τ)，其形式表述为

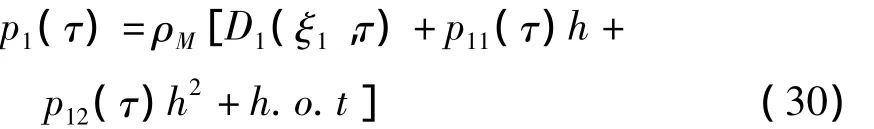
随着阶数的增高，pn的表达式变得非常冗长．若在pni(τ)中计入阻尼的影响，可以增加精度，但表达式过于繁琐．复杂计算与数值仿真表明，若要在高阶项中考虑阻尼的影响，需考虑其他方法．

经过计算得到式(35)中的的系数表达式，再令n=1，立即得到第一阶振型的表达式．pn1、pn2表达式已经在前面给出．本节则给出Dn(ξn，τ)的表达式．对于弱阻尼0 ＜ξn＜1，有:

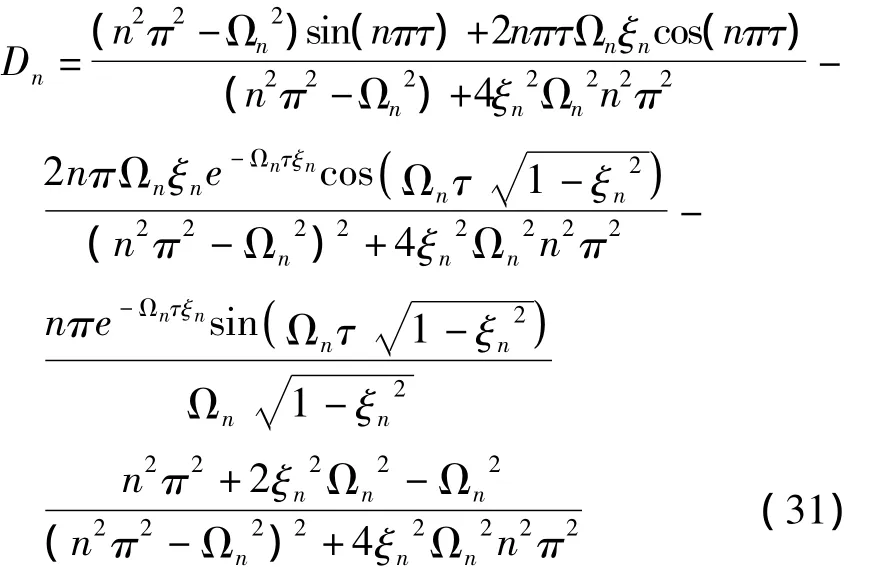
再令n=1，即得D1(ξ1，τ)表达式．数值仿真与本节解析解的比较如图5、6所示，可以看出，在在较小阻尼与Ω时，WKB解具有很好的精度．

5 结论

采用WKB法，得到了简支梁移动质量响应的解析解．通过与数值解、Inglis解的比较，得出以下结论．

1)当简支梁阻尼可以忽略时，即使移动荷载的质量是简支梁的数倍，WKB解仍然与数值解符合的很好，通常优于Inglis解与移动常力解．

2)当考虑简支梁的弱阻尼时，WKB解与数值解符合的较好，尤其是在无量纲频率小于1时．

3)简支梁移动质量的位移响应随着的增加而增加，随着无量纲频率的增加而降低．大量数值仿真表明，当阻尼、移动质量与无量纲频率 过大时，WKB法精度稍有降低．

1 Fryba L．Vibrations of solids and structures under moving loads．Academia，Prague，Noordhoff International Publishing，Groninggen，1972

2 Fryba L．Dynamics of railway bridges，Publisher:Thomas Telford，1996

3 邓学钧，孙璐．车辆－地面结构系统动力学．北京:人民交通出版社，1998(Deng X J，Sun L．Vehicle－ground structure system dynamics，Beijing:People Jiaotong Press，1998(in chinese))

4 潘家英，高芒芒．铁路车－线－桥系统动力分析．北京:中国铁道出版社，2008(Pan J Y，Gao M M．Railway vehicle－line－bridge system dynamics．Beijing:China Railway Press，2008(in Chinese))

5 李国豪．桥梁结构稳定与振动(第二版)．北京:中国铁道出版社，2003年 (Li G H．The stability and vibrations of bridges(The second edition)．Beijing:China Railway Press，2003(in Chinese))

6 Yang Y B，Yau J D，Wu Y S．Vehicle－bridge interaction dynamics with application to high－speed railways．Singapore:World Scientific Publishing，2004

7 宋一凡．公路桥梁动力学．北京:人民交通出版社，2000(Song Y F．Highway bridge dynamics．Beijing:Jiaotong Press，2000(in Chinese))

8 翟婉明．车辆－轨道耦合动力学(第三版)．北京:中国铁道出版社，2007(Zhai W M．Vehicle－rail coupling dynamics(Third edition)．Beijing:China Railway Press，2007(in chinese))

9 李广慧．车辆－无碴轨道－桥梁系统振动特性及其应用．郑州:黄河水利出版社，2007(Li G H．The vibrational properties and it applications of Vehicle－ballastless－trackbridge systems．Zhengzhou:Yellow River Water Conservancy Press，2007(in Chinese))

10 陈政清，华旭刚．人行桥的振动与动力设计．北京:人民交通出版社，2009(Chen Z Q，Hua X G．Vibration and dynamical design of pedestrian bridges．Beijing:People＇s Jiaotong Press，2009(in Chiness))

11 Guo S Q，Yang S P．Free longitudinal vibrations of non－uniform Rods．Science China Technological Sciences，2011，54(10):2735～2745

12 Guo S Q，Yang S P．Wave Motions in nonuniform one Dimensional Waveguides．Journal of Vibration and Control，2012，18(1):192～100

*The project supported by the National Natural Science Foundation of China(11072157，11272219，11227201，10932006)and the National Basic Research Program of China 973 program(2012CB723301)

† Corresponding author E－mail:guoshuqi@stdu．edu．cn

ANALYSIS OF THE DYNAMIC RESPONSE OF A SIMPLE SUPPORTED BEAM UNDER A MOVING MASS*

Guo Shuqi1†Kong Yanping1Yang Shaopu2
(1．Shijiazhuang Tiedao University，Engineering Mechanics Department，Shijiazhuang050043，China)(2．Shijiazhuang Tiedao University，Mechanical School，Shijiazhuang050043，China)

With increasing vehicle speed，traffic volume and axle load，the dynamic response of bridges under moving loads have attracted more and more attentions．In this paper，the vehicle load is simplified as moving mass，i．e．considering the inertia of the vehicle．Then the governing equation is partial differential equations with variable coefficients，which difficult to deal with in math．Using the method of separation of variables and mode superposition，the equations are reduced as ordinary differential equations with variable coefficients．By the modified WKB method，the approximate dynamical response is obtained．

simple supported beam， moving mass， WKB method

24 June 2012，

28 November 2012．

10．6052/1672－6553－2013－052

2012－06－24 收到第 1 稿，2012－11－28 收到修改稿．

*国家自然科学基金(11072157，1272219，1227201，10932006)，国家重点基础研究发展计划973项目(2012CB723301)资助项目

E－mail:guoshuqi@stdu．edu．cn