三阶剪切变形板的振动特性研究*
2014-09-17陈丽华孙玥张伟
陈丽华 孙玥 张伟
(北京工业大学机电学院,北京 100124)
三阶剪切变形板的振动特性研究*
陈丽华 孙玥 张伟†
(北京工业大学机电学院,北京 100124)
对于中厚板或层合板而言,横向剪切变形的影响是显著的,采用三阶剪切变形理论比采用经典薄板理论和一阶剪切变形理论能更好的满足精度的要求,而且能更好地描述板的剪切变形和剪应力沿厚度方向的分布情况.本文用解析的方法研究了简支、自由和固定三种边界条件的任意组合下三阶剪切变形板的自由振动问题.首先应用哈密顿原理建立自由振动方程,再通过引入中间变量使得原来耦合的自由振动方程得到解耦和简化,基于分离变量法,利用边界条件得到基函数的表达式,利用Rayleigh-Ritz法,求得三阶剪切变形板在任意边界条件下的固有频率和振型.本文得到的结果可以为厚板在工程中的应用提供理论依据,具有较高的工程实际应用价值.
板, 三阶剪切变形理论, 固有频率, 振型, Rayleigh-Ritz法
引言
在关于板振动问题的研究中,主要是基于经典薄板理论[1]、一阶剪切变形理论[2]和三阶剪切变形理论[3]这几种理论进行研究.对于厚板和层合板,采用三阶剪切变形理论比采用克希霍夫的经典薄板理论和一阶剪切变形理论能更好的满足精度的要求,而且能更好地描述板的剪切变形和剪应力沿厚度方向的分布情况.通常不同的板理论适用于不同厚度的板,一般来说,经典薄板理论适用于薄板,一阶剪切变形理论适用于中厚板,而三阶剪切变形理论适用于厚板和层合板.
对于经典薄板理论,以往许多文献研究的都是两对边简支薄板的自由振动问题.但是Leissa[4]给出了任何边界条件组合下薄板振动的精确解析解.对于中厚板,横向剪切变形和转动惯量的影响不能忽略,许多学者[5-7]基于一阶剪切变形理论用能量法[8-12]来研究板的振动问题.最近,Akhavan et al.[13]用这种方法研究了钟阳[14]等人基于此理论将中厚板自由振动问题导入哈密顿体系,然后利用辛几何中的分离变量和本征函数展开的方法求出了对边简支板自由振动的精确解.在弹性地基上受面内载荷作用的矩形Mindlin板.然而一阶剪切变形理论里的剪切修正因子的选取不仅与板的几何参数有关,还与边界条件和载荷有关.
对于三阶剪切变形理论,Reddy和 Phan[15]基于此理论给出了四边简支各向同性、各向异性和层合矩形板自由振动和屈曲问题的精确解.Dong[16]基于三阶剪切变形理论运用了平均应力法简支矩形板的振动问题.Hanna和Leissa[17]又用此理论研究了完全自由的矩形板振动问题.Matsunaga[18]基于三阶剪切变形理论通过哈密顿原理和Navier方法研究了简支矩形板的稳定性和自由振动问题.但是到目前为止,对于任意边界条件下基于三阶剪切理论的板振动问题的解析方法还没有人研究.
本文介绍了一种基于三阶剪切变形理论来研究厚板横向振动问题的解析方法,给出了求解不同边界条件下的固有频率和振型函数的过程.
1 建立自由振动方程
基于三阶剪切变形理论,位移函数的表达式可以写成:

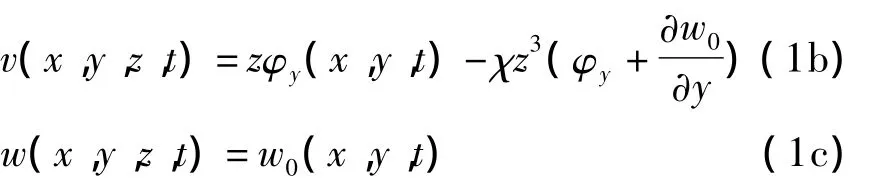
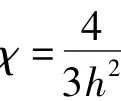
(1)式中w0为板中面内任意点(x,y)的横向位移,φx,φy分别为板中面的法线绕y轴和x轴的转角.
对曲率和应变进行以下定义:

则得到广义内力Mx,My,Mxy,Qx,Qy,Px,Py,Pxy,Rx,Ry和转动惯量Ii(i=0,3,5,7)的表达式:

E,G,h分别为板的弹性模量,剪切模量和厚度.
运用Hamilton原理,得到自由振动的方程:
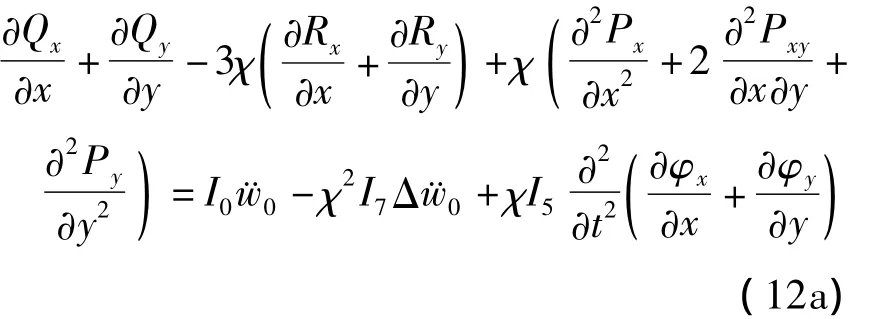

边界条件包括位移边界条件和力的边界条件两类:
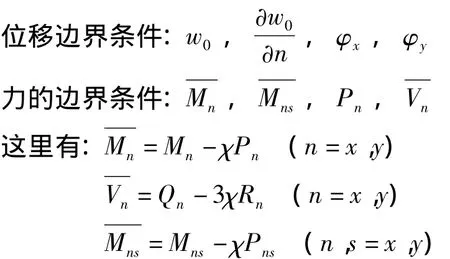
可以看出每个边上有四个边界条件,任意边界条件是指位移和力边界条件的任意组合,工程上常用的是固定、简支和自由三种情况的任意组合.
2 自由振动方程的求解
通过得到的三阶剪切变形板自由振动方程(12)式可以看出:这是3个变量w0,φx和 φy相互耦合的偏微分方程组.对于四边简支的情况,已有文献[14]直接给出了其振型函数的表达式.但是,对于任意边界条件,三阶剪切变形板自由振动解的形式不能通过分离变量的方法直接求得,因此本文通过引入中间变量,经过一系列的推导,使得原来耦合的振动方程得到解耦和简化,然后精确给出理论解的表达式.首先为了进行解耦,这里引入一个中间变量fxy,令

则(12a)式可以写为:

其中
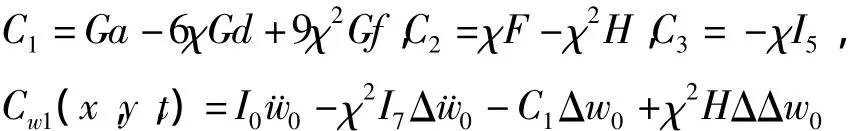
拉普拉斯算子Δ的表达式为:
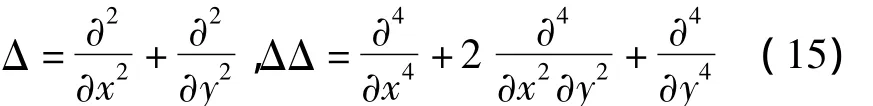
由方程(12b-c)和(13)式,方程(12a)还可以改写成下面的形式:
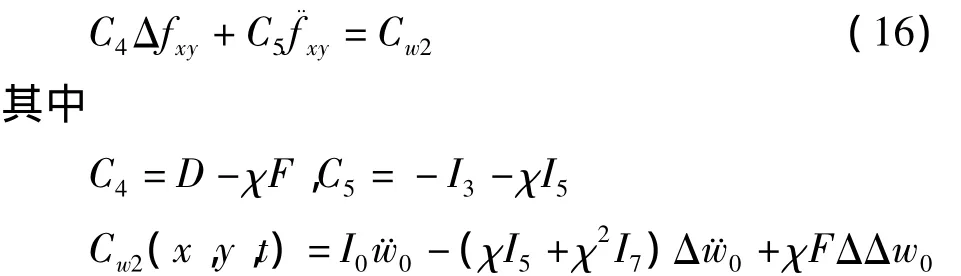
联立(14)和(16)两个方程,通过变换消去中间变量fxy,则可以得到只含挠度w0的方程:
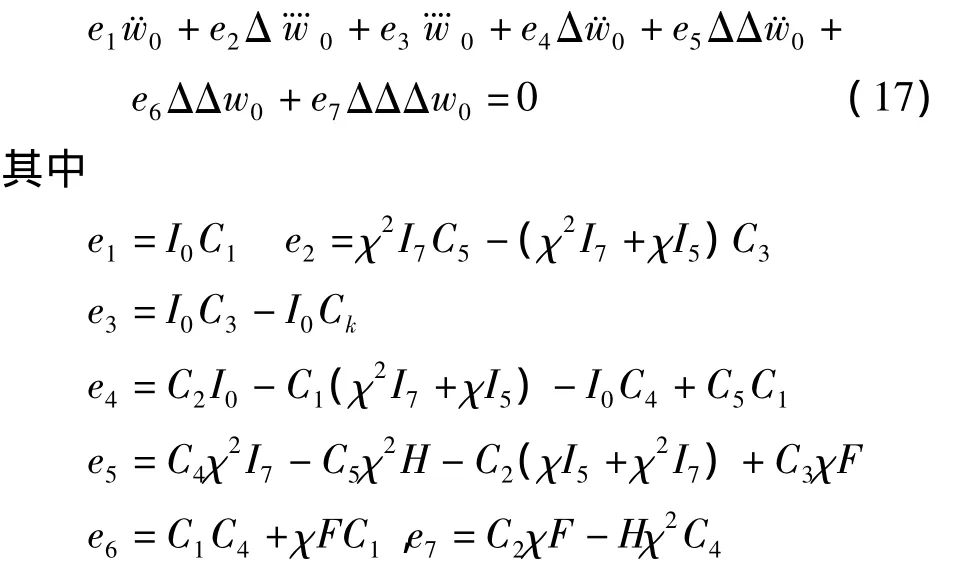
下面我们就对解耦后的方程(17)进行求解.首先将挠度w0(x,y,t)中的空间和时间变量分离,则得到解的表达式为:
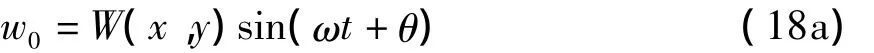
同样对于另外两个变量φx,φy有
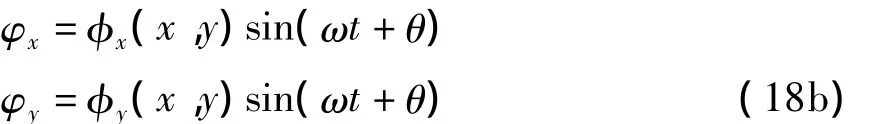
W(x,y),φx(x,y),φy(x,y)是振型函数,ω 是振动的固有频率,其中这些振型函数可以由x和y方向一系列基函数的组合来表示:
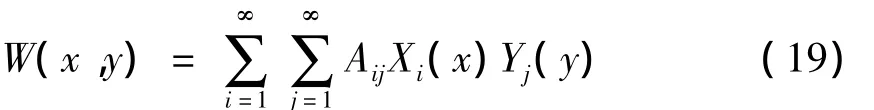
为了得到振型函数,我们需要分别求解基函数Xi(x)和Yj(y).本文将x和y方向分开考虑,以y方向为例,假设板在x方向上无限长,所有变量只与y有关,(17)式则化为

假设上式解的形式为Y(y)=esy,将其代入,于是得到一个关于s的特征方程

±s1,±s2,±s3是特征方程的根,且它们是与固有频率ω相关的.则基函数的表达式可以得到:
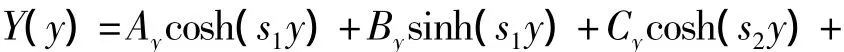
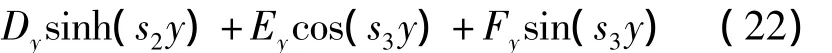
其中Ay,By,Cy,Dy,Ey,Fy是待定系数.将上式代入y方向相应的边界条件中
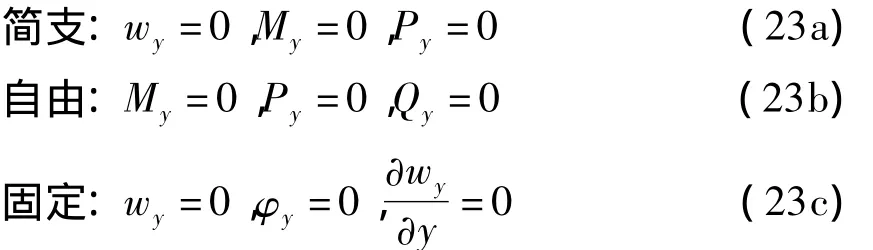
在y=0和y=b处,任取上述两个边界条件,就构成了由6个边界条件方程得到6个关于系数Ay,By,Cy,Dy,Ey,Fy的线性代数方程组,由方程组有非零解的条件,即这6个方程的系数行列式为零,从而求出各阶固有频率ωi的值.把求得的各阶固有频率代入到边界条件方程中,就求得待定系数Ayi,Byi,Cyi,Dyi,Eyi,Fyi,从而得到y方向基函数Yi(y).
对于x方向,基函数X(x)的形式与y方向相同,有
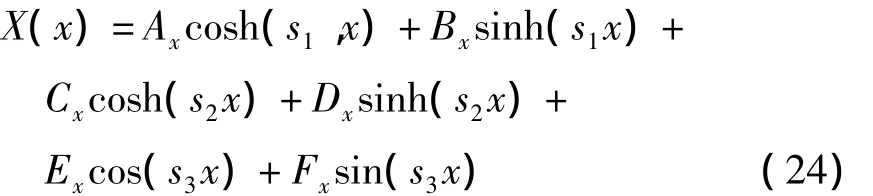
同样,x方向的边界条件有

同样方法可以得到x方向各阶基函数的表达式Xi(x).
通过解耦,并利用边界条件,挠度w0的振型函数W(x,y)就可以由求得的x和y方向基函数代入(19)式得到.下面我们开始推导转角φx和φy的振型函数.
首先求出y方向的转角基函数Φy(y)和挠度基函数Y(y)的关系.运用单向厚板的表达式,在(14)式中只考虑y方向(假设板在x方向无限长),所有变量只与y有关,可以得到:

其中
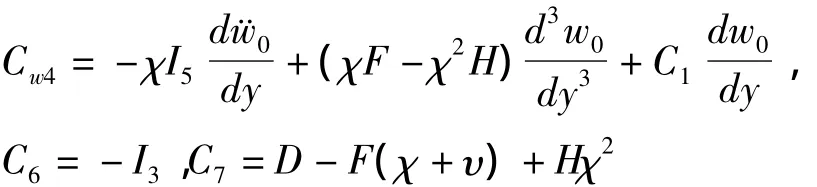
为了得到Φy(y)与Y(y)的关系,对(26)式和(27)式做了如下一系列变换和推导:
令(26)式对y求积分并移项得:

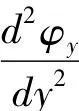
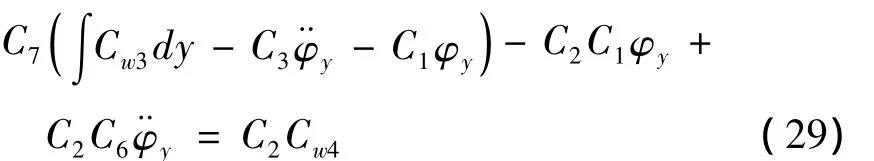
将表达式 φy(y,t)=Φy(y)·sin(ωt+θ)和w0(y,t)=Y(y)·sin(ωt+θ)代入(29)式,就可以得到Y(y)和Φy(y)的关系式:
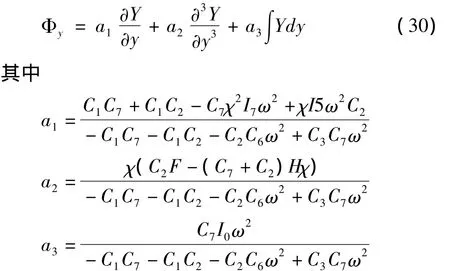
把前面得到的y方向各阶基函数Yi(y)的表达式代入到(30)式,就得到各阶y方向转角的基函数Φyi(y).同样方法可以得到X(x)和Φx(x)的关系式:

3 Rayleigh-Ritz法求固有频率和模态
对于三阶剪切变形板的自由振动问题,势能和动能的表达式可以写成:
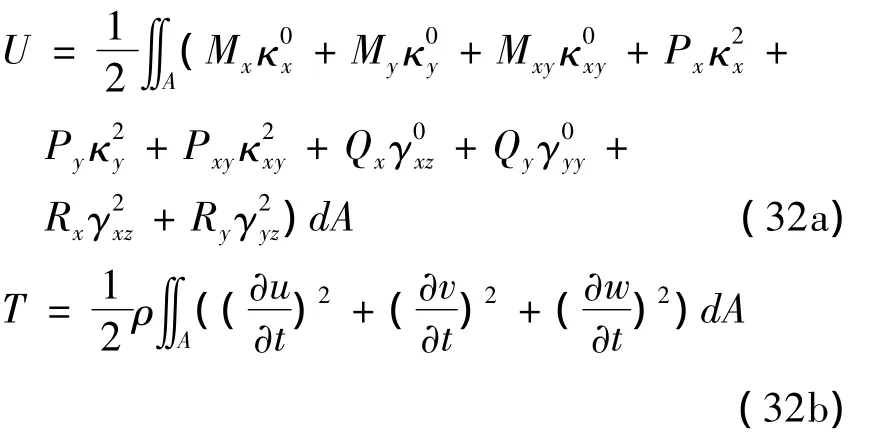
位能函数

Rayleigh-Ritz法中的试函数可以选择满足边界条件的振型函数表达式:
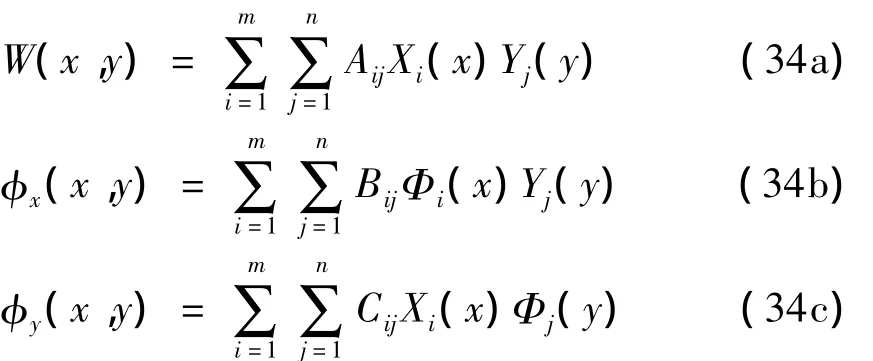
其中基函数表达式Xi(x)和Yj(y)由(22)和(24)式得到.Aij,Bij和Cij为待定系数.把(18)式代入动能的表达式(32b)式中,得到最大动能表达式
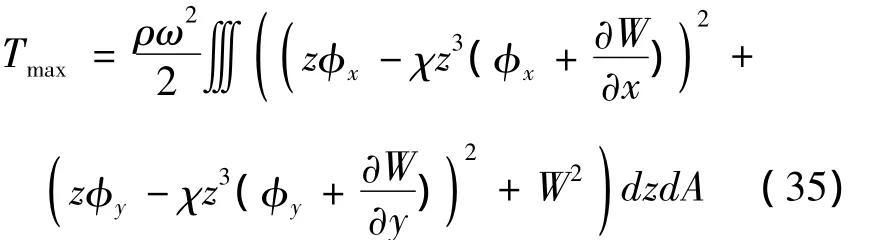
把曲率和应变的表达式(2-5)式,以及广义内力的表达式(6-8)式以及(18)式代入到势能的表达式(32a)中,得到最大势能的表达式为:
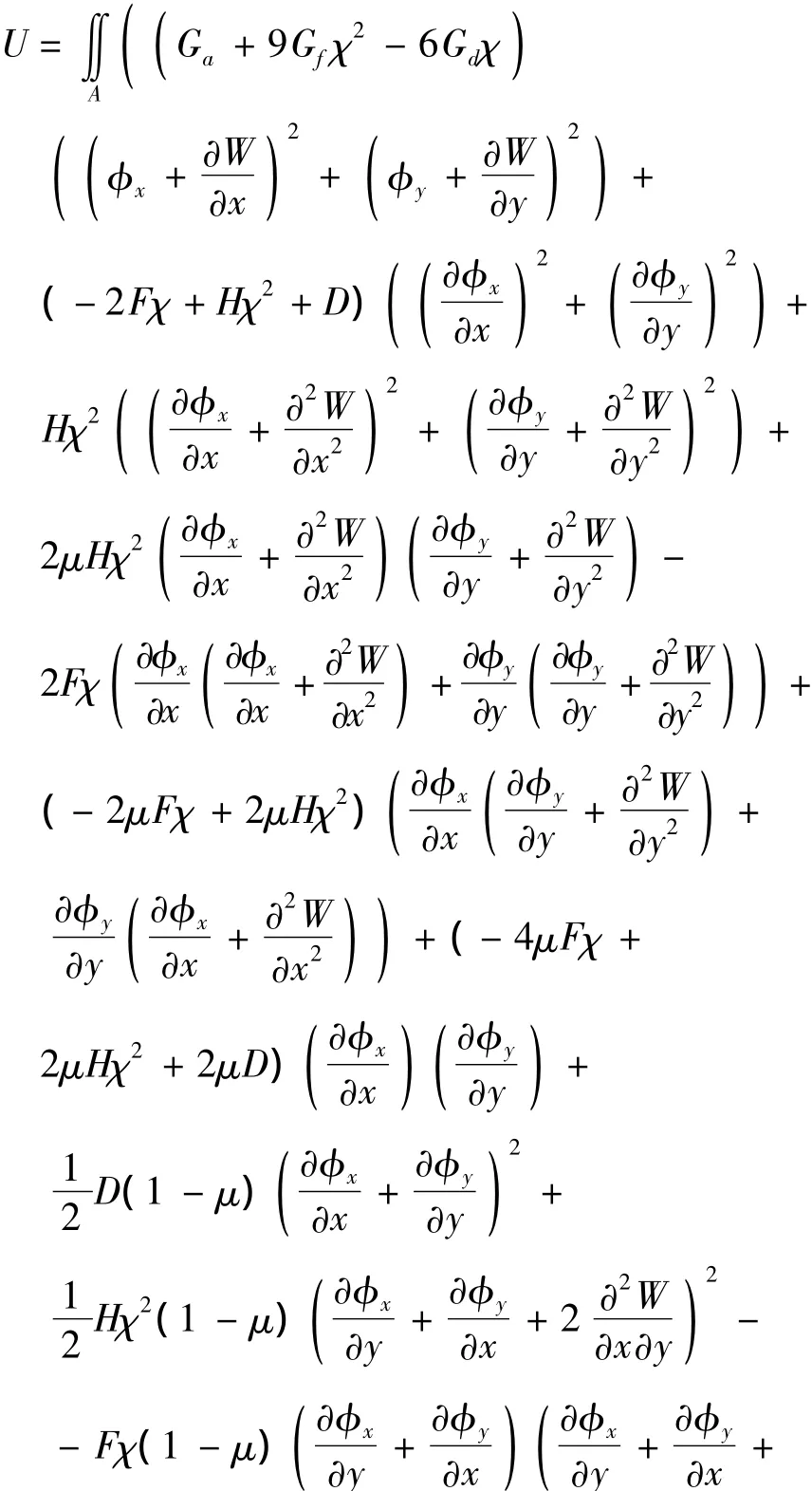

由最小位能原理,得:

由于待定系数Aij,Bij和Cij相当于独立的广义坐标,所以变分式可以简化为多元函数的极值条件:
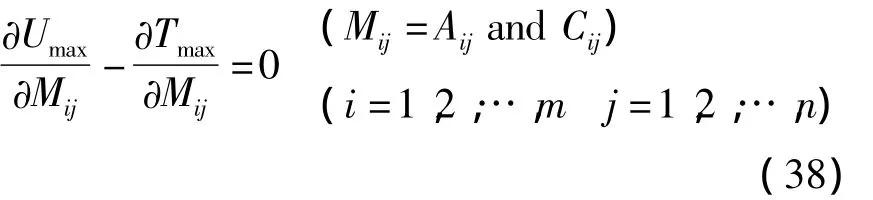
将最大动能(35)式和最大势能(36)式代入到上式中,就得到一个关于待定系数Aij,Bij和Cij的代数方程组,一共3×m×n个.由方程组有非零解的条件,令其系数行列式为零则可以求得板振动的各阶固有频率,将求得的相应各阶固有频率数值带回原方程组(37)式中,就可以求得相应各阶的模态函数.
经过验证发现,当(1)式中χ=0时,自由振动方程(12a-c)中没有与 χ有关的项,即由基于Reddy板理论所推导得到结果退化为基于Mindlin板理论推导得到的结果.此时(22)和(24)式中的s1=0,且所得到的基函数解的形式和边界条件与曹志远[18]基于Mindlin板理论研究板自由振动问题所得到的结果一致,因此可以验证本文所述的方法和推导过程的正确性.
4 结论
本文对于在不同边界条件下矩形厚板的自由振动问题给出了精确的解析解.基于三阶剪切变形理论,建立了自由振动方程,通过引入中间变量和分离变量法将三个偏微分方程转化成只含一个变量的常微分方程.将所求振型函数写成一系列x和y方向基函数的组合,再由边界条件得到基函数的表达式,代入Rayleigh-Ritz法中,得到了三阶剪切变形板在不同边界条件下固有频率和振型函数的解析表达式.
由推导的过程和结果可以得出以下结论:
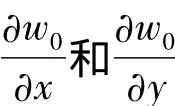
2)由所求得的挠度基函数Y(y)(或X(x))与转角基函数Φy(y)(或Φx(x))之间的关系可以看出,Φy(y)(或Φx(x))的表达式中包含一个Y(y)(或X(x))的积分形式,这也是区别于经典薄板理论和Mindlin板理论所得出的结果.
综上,本文提出的基于三阶剪切变形理论研究厚板自由振动的方法和结果,可以为强迫振动或非线性振动的研究提供理论基础,也为厚板的实际工程应用提供理论指导.
1 Timoshenko S,Woinowsky-Krieger S.Theory of plates and shells,second ed.New York:McGraw-Hill Book Company,1959
2 Mindlin R D.Influence of rotary inertia and shear on flexural motions of isotropic elastic plates.Journal of Applied Mechanics-transactions of the ASME,1951,18:31 ~38
3 Reddy J N.A simple higher-order theory for laminated composite plates.Journal of Applied Mechanics-Transactions of the ASME,1984,51:745 ~752
4 Leissa A W.The free vibration of rectangular plates.Journal of Sound and Vibration,1973,31:257 ~293
5 Leissa A W.Vibration of Plates,NASA SP-160,Office of Technology Utilization,NASA,Washington DC,1969
6 Liew K M,Xiang Y,Kitipornchai S.Research on thick plate vibration:a literature survey.Journal of Sound and Vibration,1995,180:163 ~176
7 Liew K M,Wang C M,Xiang Y,Kitipornchai S.Vibration of Mindlin Plates,Elsevier,Amsterdam,1998
8 Dawe D J,Roufaeil O L.Rayliegh-Ritz vibration analysis of Mindlin plates.Journal of Sound and Vibration,1980,69:345~359
9 Liew K M,Xiang Y,Kitipornchai S.Transverse vibration of thick rectangular plates- I.Comprehensive sets of boundary conditions.Computers and Structures,1993,49:1 ~29
10 Liew K M,Hung K C,Lim M K.Vibration of Mindlin plates using boundary characteristic orthogonal polynomials.Journal of Sound and Vibration,1995,182:77 ~90
11 Cheung Y K,Zhou D.Vibrations of moderately thick rec-tangular plates in terms of a set of static Timoshenko beam functions.Computers and Structures,2000,78:757 ~768
12 Cheung Y K,Zhou D.Vibration of tapered Mindlin plates in terms of static Timoshenko beam functions.Journal of Sound and Vibration,2003,260:693 ~709
13 Akhavan H,Sh.Hosseini Hashemi,H.Rokni Damavandi Taher,A.Alibeigloo,Sh.Vahabi,Exact solutions for rectangular Mindlin plates under in-plane loads resting on Pasternak elastic foundation.Part II:Frequency analysis,Computation Materials Science,2009,44:951 ~961
14 Reddy J N,Phan N D.Stability and vibration of isotropic,orthotropic and laminated plates according to a higher-order shear deformation theory.Journal of Sound and Vibration,1985,98:157 ~170
15 Doong J L.Vibration and stability of an initially stressed thick plate according to a higher order deformation theory.Journal of Sound and Vibration1987,113:425 ~440
16 Hanna N F,Leissa A W.A higher order shear deformation theory for the vibration of thick plates.Journal of Sound and Vibration,1994,170:545 ~555
17 Matsunaga H.Free vibration and stability of thick elastic plates subjected to in-plane forces.International Journal of Solids and Structures,1994,31:3113~3124
18 曹志远,杨昇田.厚板动力学理论及其应用.科学出版社,1983:81~120(Cao Z Y.Plate dynamics theory and applications.Beijing:Science Press,1983:81 ~ 120(in Chinese ))
*The project supported by the National Natural Science Foundation of China(11172011)
† Corresponding author E-mail:sandyzhang0@yahoo.com
STUDY ON VIBRATION CHARACTERISTIC OF THIRD ORDER SHEAR DEFORMATION THEORY OF PLATE*
Chen Lihua Sun Yue Zhang Wei†
(College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology,Beijing100124,China)
The effect of the transverse shear deformation for Reddy plates or laminated plates is significant.In this case,it can meet the requirements for calculate precision better to use the third order shear deformable theory than to use the classical thin plate theory and the first order shear deformation theory.And it is better to describe the distribution of the plate shear deformation and shear stress varying through the thickness when using the third order shear deformation theory.In this paper,an analytical method is presented for studying the free vibration characteristic of plate using the third order shear deformation theory on different boundary conditions,which are the any combinations of simply supported,free and clamped.Hamilton principle is used to formulate the free vibration equations.Then,by introducing the intermediate variable the original coupling free vibration equations are decoupled and simplified.The fundamental function expressions are obtained basing on the method of separation of variables and the boundary conditions.And the natural frequencies and modal functions are obtained by using the Rayleigh-Ritz method.The method in this paper has a good generality for solving the vibration problems of thick plates under different boundary conditions.The result obtained in this paper can provide a theoretical basis for thick plate's application in engineering,and it has relatively high application value.
plates, third order shear deformable theory, natural frequency, modal function, Rayleigh-Ritz method
14 June 2012.
10.6052/1672-6553-2013-059
2012-06-14 收到第1 稿.
*国家自然科学基金资助项目(11172011)
E-mail:sandyzhang0@yahoo.com
