Q235B钢Johnson-Cook模型参数的确定

林 莉，支旭东，范 锋，孟上九，苏俊杰

(1.哈尔滨工业大学 土木工程学院，哈尔滨 150090;2.哈尔滨理工大学 建筑工程学院土木工程系，哈尔滨 150080)

近年来，由于军用和民用领域的推动，特别是在911事件之后，冲击爆炸问题越来越受到关注。对冲击爆炸问题的研究，早期主要依赖于实验。目前，随着有限元等数值方法的发展和计算机能力的提高，基于计算机代码和数值计算软件的数值模拟方法在工程设计中扮演了越来越重要的角色［1］。然而，数值模拟的精确性和实用性极大地受到本构关系，断裂准则等材料性能表征的限制［2］。从大量的公开文献可以了解到，对材料性能好的理解和表征是获得令人满意的仿真结果的重要前提，对冲击爆炸等高度非线性问题更是如此。

如Clausen等［3］所述，在数值仿真中通常用两类模型来表征材料行为，一类表征塑性流动，另一类表征材料的断裂和失效。相比较其它模型，Johnson等［4］和Zerilli等［5-6］本构关系在冲击和爆炸领域受到了更多的关注。至于断裂准则方面，金属的延性和失效长期以来就是许多研究者关注的焦点，实验和理论方面的研究 都 有，例 如 Cockroft 等［7］，Rice 等［8］，Hancock等［9］，Mackenzie 等［10］，Johnson 等［11］。塑性变形引起的延性断裂极大地依赖于应力三轴度［9，11］，同时应变率和温度也对材料的延性断裂有不可忽略的影响。另外，最近的一些研究展示了断裂应变可能也依赖于Lode参数［12］，但其与断裂准则的关系还在进一步的研究之中。在涉及到材料动态断裂的计算领域，J-C断裂准则［11］应用的最为广泛，并且可以找到许多成功预测的案例，例如 Teng 等［14］，Gupta 等［15］。

本文研究Q235B钢在不同应变率，温度和应力三轴度下的力学性能，并建立强度和延性与各因素之间的关系。为此，开展了准静态下从20℃到950℃光滑圆棒试样拉伸试验，室温下不同应变率的光滑圆棒拉伸试验，缺口试样拉伸试验，圆柱压缩试验，光滑圆棒试样的扭转试验以及霍普金森杆拉伸试验。结合数值仿真标定J-C 强度模型［4］和 J-C 失效模型［11］的参数。为了更精确地拟合实验数据，对J-C强度和失效模型进行了适当的修改。最后通过Taylor试验验证了所获取参数的有效性。

1 本构关系和断裂准则

1.1 Johnson-Cook本构关系及参数获取方法

J-C本构关系表达式如下:

其中:A、B、n、C 和 m 为模型参数;σeq为等效应力;εeq为等效应变;为无量纲化等效塑性应变率，为参考应变率;T*=(T-Tr)/(Tm-Tr)为无量纲化温度，其中，Tr，Tm分别为参考温度和材料的熔点，T为当前温度。方程(1)右边三项分别代表等效塑性应变，应变率和温度对流动应力的影响。

参数A，B和n可以通过参考应变率和参考温度下光滑圆棒拉伸试验获得(当然，通过薄壁圆管的扭转试验也可以得到)。在参考应变率和参考温度下，方程(1)可写为，在初始屈服点，也就是 εeq=0时，σeq=σy=A，这里σy是屈服应力。A通常取为单向拉伸试验屈服时的工程应力，B和n通过拟合等效应力应变数据获得。

应变率敏感参数C和温度软化参数m可以通过标定不同应变率和不同温度下单向拉伸试验数据获得。通过方程(1)，参考应变率下屈服应力和温度的关系可写为σeq=A(1－T*m);同样，在室温下屈服应力和应变率的关系可写为)。温度软化参数m可以通过研究在不同温度下的屈服应力获得;同样地，应变率敏感参数C可以通过标定材料在不同应变率下的屈服应力获得。

此外，还应该考虑高应变率造成的温度升高。假设加载过程为绝热的，材料温度的升高可以用塑性功的消耗来表示，即，其中，ρ是材料密度，Cp是比热容，χ是塑性功转热经验系数，通常取χ=0.9［16］。

1.2 Johnson-Cook断裂准则及参数获取方法

累计损伤准则认为当损伤参量D超过单位1时，材料失效。累计损伤参量D定义为，式中 Δεeq是一个积分循环的等效塑性应变增量，εf是当前时间步下的有效断裂应变。在J-C断裂准则［11］中，有效断裂应变εf写为如下形式:

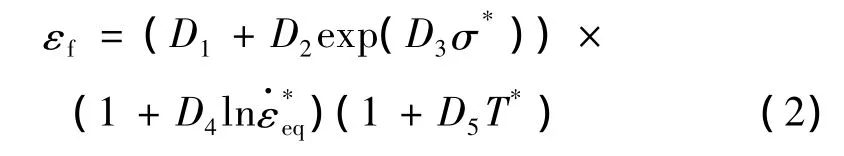
其中:D1～D5是材料常数，σ*=σH/σeq是应力三轴度，σH是平均应力。

根据方程(2)，在参考应变和参考温度下，断裂应变与应力三轴度的关系变为 εf=(D1+D2exp(D3σ*))。因此D1～D3可以通过执行参考应变率和参考温度下不同应力三轴度实验来获得。不同的应力三轴度通过压缩、剪切和缺口试件拉伸试验实现。单向压缩试验σ*=-1/3，纯剪切试验σ*=0，单向拉伸试验 σ*=1/3。对缺口拉伸试验，通过 Bridgman［17］的研究，初始应力三轴度可以通过下式计算:σ*0=1/3+ln［1+a/(2R)］，其中，a和R分别是试件当前横截面的半径和缺口处的曲率半径。

应变率影响常数D4能通过参考温度下不同应变率拉伸试验获得，同样温度影响常数D5能通过参考应变率下不同温度拉伸试验获得。通过方程(2)，在参考温度下，断裂应变与应变率的关系为 εf=(D1+，通过执行一系列同样温度和同样应力三轴度下不同应变率试验，获得断裂应变，在D1～D3已知的前提下，拟合断裂应变-应变率实验数据可以得到应变率影响参数D4。在参考应变率下和同样的应力三轴度下，断裂应变和温度的关系变为εf=(D1+D2exp(D3σ*))(1+D5T*)，同样地，执行一系列同样应力三轴度和参考应变率下不同温度的实验，获得断裂应变，在D1～D3已知的前提下，拟合断裂应变-温度实验数据可以得到温度影响参数D5。

2 材料性能实验

本文研究的Q235B低碳钢是一种在我国广泛使用的工程结构用钢。所有实验试件来自同一根15 mm直径的Q235B钢棒。表1给出了Q235B钢的材料组成成分。基于前面的分析，为了标定本构关系(方程1)和断裂准则(方程(2))，开展了四个系列的材料性能测试。表2给出了这几种材料性能测试与获取相关参数的关系。图1给出了各种试件几何形状及尺寸。

压缩试验、缺口拉伸试验、高温拉伸试验以及室温下圆棒试样较低应变率(10-4～10-1)下拉伸试验在Inston 5569万能实验机上进行。高应变率下拉伸试验在SHTP设备上进行。设备详情可以参考文献［18］。

通过文献［19］，Q235B钢的杨氏模量 E=200 GPa，泊松比 v=0.3，比热容 Cp=469 Wm-1K-1，密度 ρ=7 800 g/m3，熔化温度Tm=1795 K。

图1 试件的形状和尺寸Fig.1 Geometry and dimensions of specimens(in mm)

室温下光滑圆棒试样准静态拉伸试验名义应变率8.33×10-4s-1。在实验中，用标距长度10 mm的夹式引伸计记录试件的伸长量，获得的载荷-位移曲线。

开展了从150～950℃光滑圆棒试样参考应变率下拉伸试验。图2给出了所有试验的载荷-位移曲线(包括室温时的)，除室温以外，其它的拉伸位移均来自试验机的横梁位移。可以明显的看出，在室温，150℃，350℃时，载荷位移曲线有明显的屈服平台，但在更高的其它三个温度下却没有。

为了获得屈服应力和断裂应变与应变率的关系，开展了室温下不同应变率的拉伸试验。低应变率(10-1s-1以下)时采用万能试验机不同速度的拉伸试验，高应变率采用SHTB动态拉伸试验。在万能试验机拉伸试验中，采用10 mm标距的引伸计测量拉伸位移。图3和图4给出了获得的应力应变曲线，从图中可以看出，大部分的试验结果都存在明显的屈服过程。

表1 Q235钢的组成成分Tab.1 Components of Q235 steel(wt.%)

表2 总的试验分类Tab.2 Survey of experimental program

为了获得较宽的应力三轴度范围，缺口拉伸试验选用了三种试件，即缺口半径R分别为2 mm，3 mm和9 mm。在试验中为了监控缺口区域的延伸量，缺口半径为2 mm和3 mm的试件采用10 mm标距的引伸计，而缺口为9 mm的试件采用20 mm标距的引伸计。图5给出了不同缺口试件的拉伸试验载荷位移曲线。可以看出，延性随着缺口半径的增大而增长了。

为了考察材料延性在负的应力三轴度下特性，开展了圆柱压缩试验。不够理想的是，六个压缩试验都没能将圆柱试件压裂。图6给出了压缩试验的载荷位移曲线，这里位移指的是试验机的横梁位移。

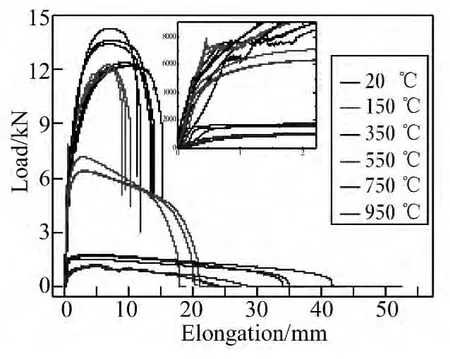
图2 不同温度下Q235B拉伸试验载荷位移曲线Fig.2 Load-elongation curves of Q235B steel at different temperatures

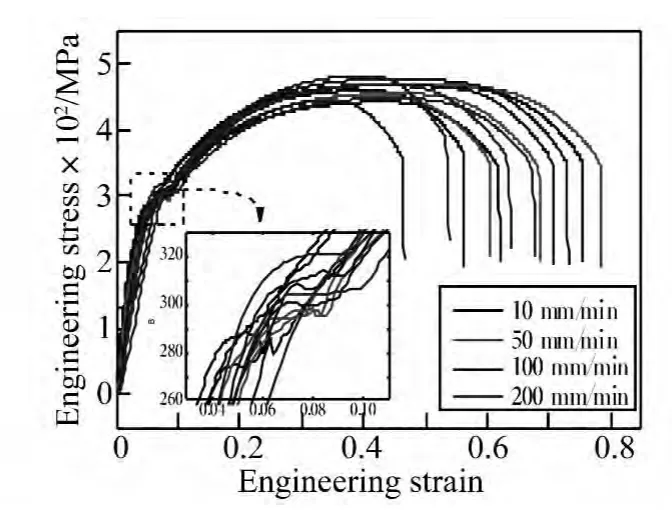
图3 单向拉伸试验不同拉伸速度下的载荷位移曲线Fig.3 Stress-strain curves obtained by using the universal testing machinein different loading velocities

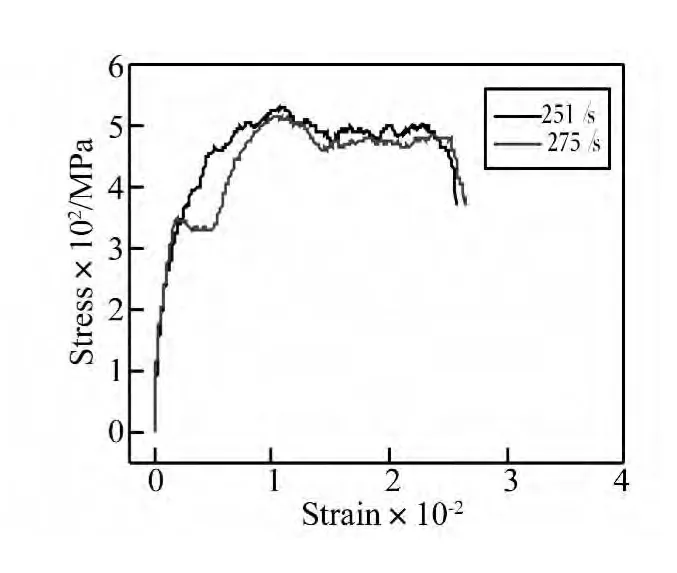
图4 霍普金森拉杆动态拉伸试验获得的应力应变曲线Fig.4 Stress-strain curves obtained by using the Split Hopkinson Tension bar

图5 不同缺口试样拉伸载荷位移曲线Fig.5 Load-elongation curves of differently pre-notched cylinder specimens

图6 圆柱压缩试验载荷位移曲线Fig.6 Load-displacement in the upsetting tests

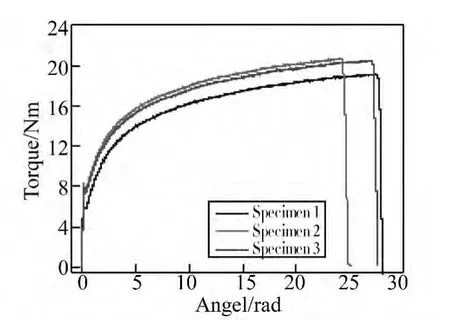
图7 扭转试验获得的扭矩转角曲线Fig.7 Torque-angle curves in the torsion tests

为了获得σ*=0时的断裂应变，开展了光滑圆棒扭转试验。在扭转试验机上，光滑圆棒试样一端固定，另一端施加扭矩，但是不约束其轴向位移。图7展示了获得的扭矩-转角曲线，这里转角指的是施加扭矩的一端试件转动的角度。从图中可以看出扭转试验中明显的屈服过程。三个扭转试样扭断后断口表面都非常平齐，这暗示了Q235B钢是延性非常好的材料。

图8给出了各种拉伸试样断裂后的典型形式。

图9 单向拉伸试验颈缩前流动行为的曲线拟合Fig.9 Curve fitting result of the flow behavior of a uniaxial tensile test before necking

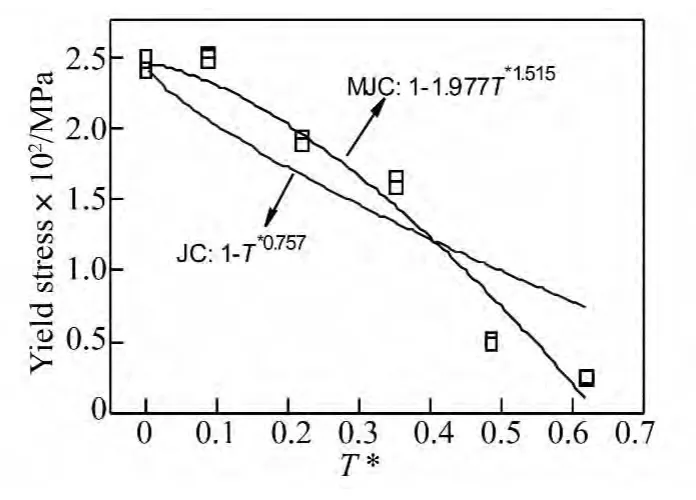
图10 不同温度下的屈服应力Fig.10 Yield stress at different temperatures

图11 不同应变率下的屈服应力Fig.11 Yield stress at various strain rates

3 强度模型和断裂准则的标定

3.1 标定强度模型

3.1.1 确定参数A，B 和n

处理单向拉伸试验数据得到平均屈服应力σy=244.8 MPa，也就是说 A=244.8 MPa。通常，应该在更大的应变范围内来标定B和n，但是由于在颈缩点之后的真应力应变需要颈缩位置直径变化信息，而这在我们目前的试验条件下无法获得，因此仅仅采用颈缩点之前的塑性流动曲线来标定B和n。由于材料本身延性非常好，颈缩之前试件变形已经非常大了。拟合实验数据得到B=899.7 MPa和 n=0.940，图9给出了拟合结果。

3.1.2 确定参数m

图10总结了在相同名义应变率下不同温度对应的屈服应力。使用方程1原始的J-C本构关系拟合得到m=0.757。然而，图10清楚的展示了原始J-C模型中的温度项形式不能合理的描述Q235B的温度软化行为。为了提高模型的预测能力，将J-C模型中原始的温度项(1-T*m)改为(1-FT*m)，其中F和m是温度软化参数。此时修改的J-C本构关系表达为

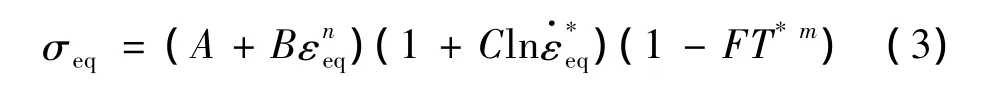
这样，原始的J-C本构变成了方程(3)的一个特例，即F=1时代表原始的J-C本构。用修改了的JC 本构拟合实验数据得到 F=1.989，m=0.151 5。很明显，如图10所示，修改后的J-C本构模型相对于原始J-C本构模型能对不同温度下单向拉伸的屈服应力给出更好的拟合。

3.1.3 确定参数C

图11总结了图3和图4中室温(20℃)下不同应变率拉伸试验各应变率对应的屈服应力。用方程1拟合实验数据得到C=0.039 1。在改变的J-C本构模型，即方程3中，C值与原始J-C模型一致。

3.2 断裂准则的标定

3.2.1 参数 D1，D2和 D3的确定

拉伸试验，包括光滑圆棒单向拉伸试验和缺口拉伸试验，断裂应变可以按式εf=ln(A0/Af)计算，其中，A0是原始的横截面积，Af断裂时断口区域横截面积。从图8中可以看出，Q235B钢光滑圆棒单向拉伸和缺口拉伸试验后试样典型的断口形式是“杯锥口状”的。

σ*=0时对应的断裂应变不能通过光滑圆棒扭转试样直接获得。对于这种情形，公开的文献通常借助于有限元计算来弥补，例如文献［21］。使用ABAQUS/STANDARD建立扭转试验的二维轴对称有限元模型，如图12所示。加载方式与试验相同，将真应力应变关系输入有限元软件，并监控参考点的扭矩和转角，得到的扭矩-转角曲线与试验比较，一旦仿真得到的扭矩-转角曲线与试验比较接近，就可以从仿真中精确获得断裂应变。

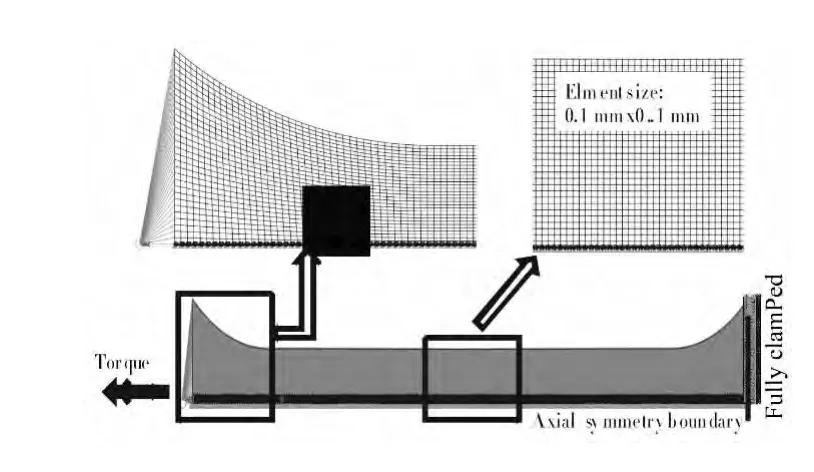
图12 扭转试验的有限元模型Fig.12 Finite element model of the torsion test

最初，把通过光滑圆棒单向拉伸试验获得的参数，也就是 A=244.8 MPa，B=899.7 MPa，n=0.940 作为真应力应变关系输入软件进行试算，发现得到的屈服之后的扭矩-转角曲线与试验结果不是非常一致。为了得到更接近的扭矩转角曲线，对参数B和n进行了适当的调整，最后发现，当 A=244.8 MPa，B=400.0 MPa，n=0.360时，仿真和试验结果一致性比较好，如图13所示。假设数值计算在断裂点预测到了和试验相同的变形角度，可以得到断裂应变为1.175。

在公开文献［4，21］中发现，材料在单向拉伸和扭转下的流动行为通常是不完全相同的，因此，本文的处理方法应该是比较合理的。

图14总结了通过光滑圆棒单向拉伸试验，缺口拉伸试验和扭转试验的应力三轴度对应的断裂应变，拟合得到 D1=-43.408，D2=44.608 ，D3=-0.016。

3.2.2 参数 D5的确定

计算出参考应变率下不同温度光滑圆棒单向拉伸试验对应的断裂应变。图15总结了断裂应变数据并用原始J-C断裂准则进行了拟合，可以看出，原始J-C断裂模型中线性形式的温度项不能很好地拟合试验结果。为了改善拟合效果，将J-C断裂模型中的温度项修改为1+D5exp(D6T*)，修改后的J-C断裂准则变为

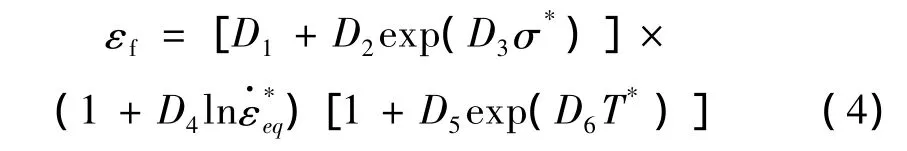
修改后断裂准则的拟合结果也展示在了图15中，拟合得到 D5=0.046，D6=7.776。可以看出，修改形式的断裂准则能对试验结果给出更好的拟合。

3.2.3 确定参数 D4

由于SHTB装置能提供的拉伸载荷有限，试验中没有得到拉断的试件，因此，仅采用万能试验机上得到的不同应变率拉伸试验的数据进行拟合，得到参数D4=0.014 5。图16总结了不同应变率下的试验数据并给出了曲线拟合结果。

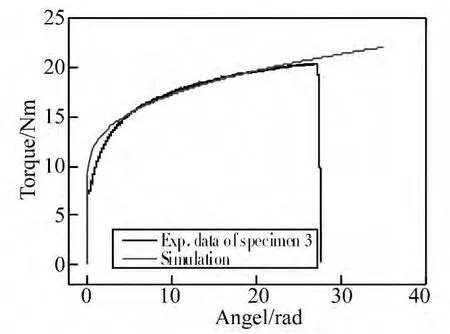
图13 扭矩-转角曲线仿真与试验比较Fig.13 Comparison of the torque-angle curves obtained by finite element simulation and experiment

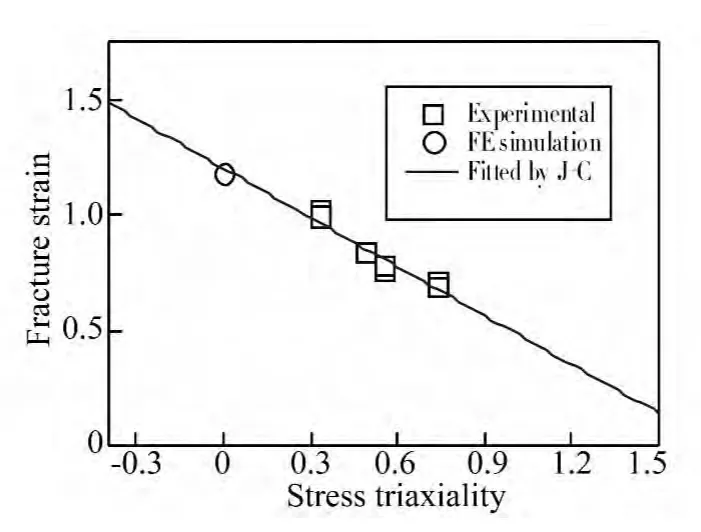
图14 断裂应变与应力三轴度关系Fig.14 Fracture strain versus stress triaxiality

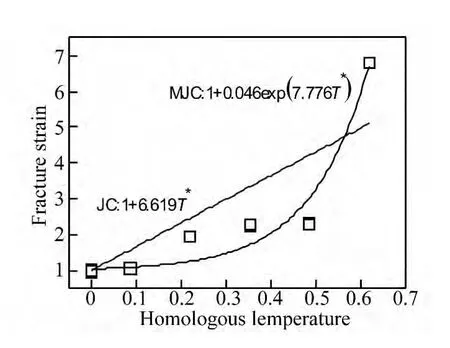
图15 拉伸断裂应变与温度的关系Fig.15 Fracture strain of specimens under tension vs temperature

4 模型参数验证

轻微修改形式的J-C模型参数都已经得到，为了验证模型参数的有效性，开展了一组Taylor试验。弹体为和前文同一根钢棒上取下的Q235B平头弹，靶板为高强装甲钢靶。使用ABAQUS软件进行与试验对应的数值模拟，建模方法及靶板材料模型和参数来自文献［21］。图17给出了数值仿真结果和试验结果的比较，可以看出，模拟结果和试验结果吻合很好，这验证了本文所获取模型参数的有效性。

图16 室温下拉伸断裂应变与应变率的关系Fig.16 Fracture strain of specimens under tension at the reference temperature vs strain rate

图17 数值仿真和Taylor试验结果比较Fig.17 Comparison of numerical simulation and Taylor test results

5 结论

本文展示了Q235B钢在不同应变率、温度和应力三轴度下的实验数据。获取了轻微修改J-C本构和失效模型的所有模型参数，并对得到的模型参数有效性进行了验证。

重要结果如下:

(1)随着温度升高，Q235B钢强度变小，延性增加。温度增加到950℃时，屈服应力仅有约25MPa，不到室温时的1/10。

(2)Q235B钢随应变率的增加，强度增加，延性减小。

(3)随着应力三轴度的增加，Q235B钢延性减小。

(4)总的来说，Q235B钢强度和延性属性可以以原始的J-C本构和失效模型为特征。然而，屈服强度的温度软化和延性的非线性温度软化效应不能得到合适的描述。本文对这两项进行了轻微的的修改，获得了很好的效果。

［1］Kane A，Børvik T，Hopperstad O S，et al.Finite element analysis of plugging failure in steel plates struck by blunt projectiles［J］.J Appl Mech，2009，76(5):051302-1-11.

［2］Zukas J A，Nicholas T，Swift H F，et al.Impact Dynamics［M］.New York:Wiley，1982.

［3］Clausen A H，Børvik T，Hopperstad O S，et al.Flow and fracture characteristics of aluminium alloy AA5083-H116 as function of strain rate，temperature and triaxiality［J］.Mater Sci and Eng A，2004，364:260-272.

［4］Johnson G R，Cook W H.A constitutive model and data for metals subjected to large strains，high strain rates and high temperatures［M］.In:Seventh International Symposium on Ballistics.The Netherlands:The Hague，1983:1-7.

［5］Zerilli F J，Armstrong R W.Dislocation-mechanics-based constitutive relations for material dynamics calculations［J］.J Appl Phys，1987，61:1816-1825.

［6］Zerilli F J，Armstrong R W.Dislocation mechanics based analysis of material dynamics behavior:enhanced ductility，deformation twinning，shock deformation，shear instability，dynamic recovery.J Phys IV Colloq［J］.C3 Suppl J Phys III 1997，7:637-642.

［7］Cockroft M G，Latham D J.Ductility and the workability of metals［J］.J Inst Metals，1968，96:33-39.

［8］Rice J R，Tracey D M.On the ductile enlargement of voids in triaxial stress fields［J］.J Mech Phys Solids 1969，17:210-217.

［9］Hancock J W，Mackenzie A C.On the mechanisms of ductile failure in high strength steels subjected to multi-axial stressstates［J］.J Mech Phys Solids，1976，24:147-169.

［10］Mackenzie A C，Hancock J W，Brown D K.On the influence of state of stress on ductile failure initiation in high strength steels［J］.Engng Fracture Mech，1977，9:167-188.

［11］Johnson G R，Cook W H.Fracture characteristics of three metals subjected to various strains，strain rates，temperatures and pressures［J］.Eng Fract Mech，1985，21:31-48.

［12］Wierzbicki T，Bao Y，Lee Y W，et al.Calibration and evaluation of seven fracture models［J］.Int J Mech Sci，2005，47:719-743.

［13］Bai Y，Wierzbicki T.A new model of metal plasticity and fracture with pressure and Lode dependence［J］.Int J Plast，2008，24:1071-1096.

［14］Teng X，Wierzbicki T， Hiermaier S， et al.Numerical prediction of fracture in the Taylor test［J］.Int J Solids Struct，2005，42:2929-2948.

［15］Gupta N K，Iqbal M A，Sekhon G S.Effect of projectile nose shape，impact velocity and target thickness on the deformation behavior of layered plates［J］.Int J Impact Eng，2008，35:37-60.

［16］Bai Y，Dodd B.Adiabatic shear localization:occurrence，theories and applications［M］. New York:Pergamon Press，1992.

［17］Bridgman P W.Studies in large plastic flow and fracture［M］.New York:McGraw-Hill，1952.

［18］Lin M，Pang B，Zhang W.Dynamic tensile behavior of Al-6Mg alloy with three treatment states［M］.DYMAT 2009，2009:1125-1131.

［19］Chen X W，Chen G，Zhang F J.Deformation and failure modes of soft steel projectiles impacting harder steel targets at increasing velocity［J］.Exp Mech，2008，48:335-354.

［20］Mae H，Teng X，Bai Y，et al.Calibration of ductile fracture properties of a cast aluminum alloy［J］.Mater Sci and Eng A，2007，459:156-166.

［21］肖新科.双层金属靶的抗侵彻性能和Taylor杆的变形与断裂［D］.哈尔滨:哈尔滨工业大学，2010.