一种大振幅超声变幅杆设计
2014-09-05潘巧生刘永斌贺良国潘成亮邓知森
潘巧生,刘永斌,2,贺良国,潘成亮,3,邓知森
(1.中国科学技术大学 精密机械与精密仪器系,合肥 230027;2.安徽大学 机械工程系,合肥 230039;3.香港中文大学 深圳研究院,广东 深圳 518057)
超声变幅杆是功率超声设备中的关键部件,主要用于实现能量传输和聚能的作用。在高声强超声如超声加工、超声焊接等应用中,辐射面一般需要几十到几百μm的振动幅度,通常在换能器上连接超声变幅杆以实现其振幅的要求,因此对于变幅杆振幅放大的研究尤为重要[1]。
按照振动类型,超声变幅杆可以分为纵振、扭振、弯振和复合振动四类,其中,在功率超声加工和处理中,纵振型应用最为普遍。按照母线形状分类,常见的变幅杆有阶梯[2-3],指数[4],圆锥[5],悬链线[6]等类型,常见变幅杆的性能特点如表1所示。其中,阶梯型变幅杆放大系数最大,但由于应力分布集中,工作安全性较差。为了综合考虑放大系数和变幅杆上的最大应力,利用ANSYS优化设计,以变幅杆放大系数为目标函数,以发生在杆的最大应力和工作频率为状态变量,可获得新型变幅杆。例如Wang等[7]设计了一种贝兹尔曲线截面的变幅杆,在相同的面积系数下,这种形状变幅杆比悬链线形变幅杆振幅增加了71%,而最大应力减小了58%。

表1 常见的几种变幅杆优缺点比较
在实际应用中,超声变幅杆的性能最常见的参数有工作频率,放大系数M,形状因数φ。以往对提高变幅杆振幅的设计都是以增大放大系数M为目标,而本文则以提高变幅杆形状因数φ为目标。
本文研究变幅杆工作时振动状况,基于变截面杆波动方程,研究一种确定频率的大振幅变幅杆。同时通过对比不同形状变幅杆振动情况,验证理论设计的准确性。
1 大振幅变幅杆设计理论
1.1 变幅杆形状的设计
图1所示为一种由郎之万振子与变幅杆构成的压电换能器,工作频率为55.7 kHz。其中振子由压电陶瓷环堆,前、后盖板,预紧螺栓等组成。振子后盖板上的法兰位于系统振动节点处,用于固定。通过合理地设计变幅杆的形状,当受到振子的激励时,变幅杆处于一阶纵向振动模态,并实现振动振幅的放大,其位移曲线示意图如图1所示。

图1 郎之万振子与变幅杆示意图
为了获得大振幅变幅杆,首先分析一段细长等截面杆在受到纵向激励下的一阶共振状态。图2(a)所示为一等截面细长杆,当等截面杆达到一阶纵振模态时,在其中间节点处的位移始终为零,而应力最大。等截面杆的振幅取决于节点后1/4波长段的最大拉伸长度,而这又受变幅杆材料所能承受应力的限制[7],即发生在节点处的最大应力不能超过材料的疲劳极限。设想如果有一种变幅杆如图2(b)所示,发生在变幅杆上的最大应力不仅位于节点处,而且在节点后持续很长一段长度l2,理论上l2不超过1/4波长。当空载时,变幅杆末端应力理论上为0,为了实现这种过渡,在变截面后段加一段长为l3等截面杆作为过输出端,那么这种形状的变幅杆就能获得相同材料变幅杆的理论最大值。为了获得等应力变幅杆,根据变截面杆波动方程(1),计算节点后应力均匀分布段杆的轮廓曲线,然后利用ANSYS有限元仿真,使得应力最大值发生在应力均匀分布处。

图2 (a)等截面杆及应力分布 (b)等应力杆及应力分布
细长变截面杆的纵向振动波动方程如下:
(1)
其中:x为沿杆长度质点坐标值,ξ(x)为质点位移函数,S(x)为杆的横截面积函数,k为圆波数。
要使得杆上每一处应力大小分布均匀,则应变与x值无关,此时位移分布函数可以表示如下:
(2)
令:
(3)
其中:ξl为x=l处质点振动位移的大小,ω为圆频率。将式(2)、(3)代入式(1),可解得:
(4)
(5)
(6)
其中:R(x)为轮廓半径函数,R0为节点处半径。由式(4)、(5)、(6)可知,S(x)、R(x)、l2和l3不仅取决于变幅杆始端和末端截面面积,还与变幅杆的材料有关。变幅杆始端半径主要取决于振子连接处,本文取R0=3.18 mm,末端面积取决于工具头,本文取Rl=0.5 mm。表2所示三种不同材料等应力变幅杆的几何参数,其中x为杆长。
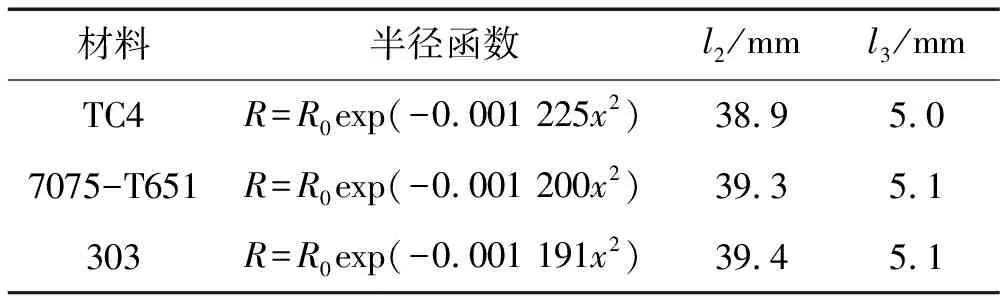
表2 三种材料等应力变幅杆几何参数
1.2 变幅杆材料的选择
变幅杆对材料的要求主要有:①在其工作的频率范围内材料的耗损小,②材料的疲劳强度高,而声阻抗率小,③易于机械加工[8]。适合以上要求的材料主要有铝合金,钛合金等。由图2可知,l2≫l3,所以可以近似认为l2段拉伸长度为变幅杆的振幅而忽略l3的拉伸长度。由胡克定律:
(7)
其中:σmax为发生在变幅杆上的最大应力,E为材料的杨氏模量,l2为等应力段长度(如表2所示),计算结果如表3所示。表3所示为303不锈钢,7075-T651铝、TC4钛合金三种材料的抗疲劳强度[σ]和变幅杆所能达到的极限振幅Dmax。
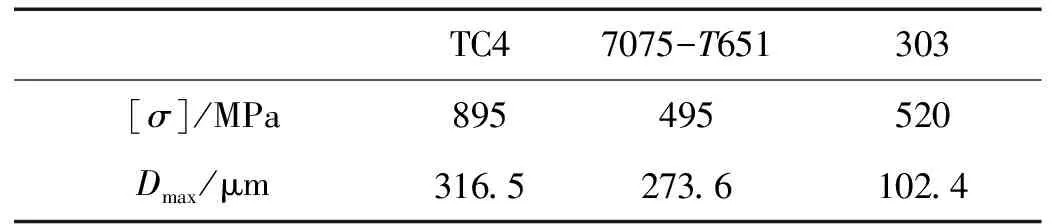
表3 三种材料的疲劳强度及对应理论最大振幅
2 仿真设计
为了使上述设计的变幅杆应力最大值发生在应力分布均匀处,采用ANSYS软件分析换能器系统的振动模态,调节变幅杆l1的长度,使换能器系统一阶共振频率为振子的工作频率,即55.7 kHz附近,再利用ANSYS谐响应分析,确认变幅杆的最大应力发生在所设计的等应力处,从而确定变幅杆的形状参数。
2.1 模型的建立与模态分析
在三维设计软件Unigraphics NX 7.5(UG NX7.5)中建立郎之万振子与等应力变幅杆装配体三维模型及其各部分尺寸如图3(a)所示,将模型导入到ANSYS软件,并进行网格划分如图3(b)所示,网格划分采用自由划分方式,网格划分中压电陶瓷环片的单元类型选用六面体20节点单元的solid226,其他各个部分都选用三维20节点结构单元的solid95。其中,前后盖板的材料分别为303不锈钢和7075-T651铝,压电陶瓷堆是由四片沿z方向极化的PZT4压电陶瓷环组成,相邻两片陶瓷片的极化方向相反,预紧螺栓和变幅杆的材料都为TC4钛合金,各材料参数如表4所示。
由前述变幅杆设计理论可知,换能器的固有频率和节点位置可以通过改变l1的值来调节。以l1为变量,以超声换能器系统工作频率为55.7 kHz为目标,优化l1长度,可得l1长度与固有频率之间的关系表5所示。当l1=21 mm时,系统的固有频率为55.735 kHz,系统位移云图如图3(c)所示。
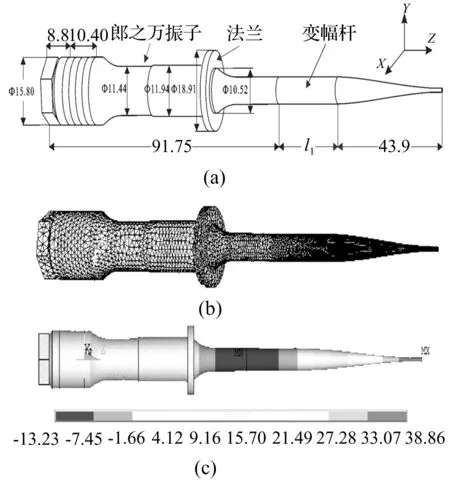
图3 (a)装配体示意图(b)三维有限元网格划分(c)ANSYS模态分析位移云图

表4 压电陶瓷(PZT4),7075-T651铝,303不锈钢,和TC4材料参数
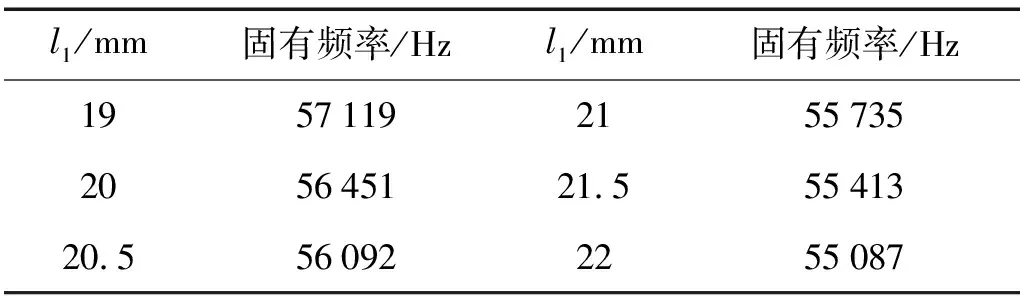
表5 l1长度与固有频率的关系
2.2 谐响应分析
谐响应分析是用于确定线性结构在承受随时间按正弦规律变化的载荷时的稳态响应的一种技术。利用ANSYS谐响应技术可以分析和计算当变幅杆受到一定频率激励时,其应力分布状况和大小。
在ANSYS谐响应分析中,施加在压电陶瓷上激励电压峰峰值为1V,频率为模态分析所获得的频率,即55 735 Hz。分析后,后处理观察沿杆等效应力分布云图如图4(a)所示,由图可知,变幅杆应力沿节点后的位置分布均匀,同时也是整个变幅杆应力分布最大处。图4(b)所示为变幅杆应力分布曲线。
为了比较所设计的等应力变幅杆与其他常见形状变幅杆能获得最大振幅的关系,同时设计了固有频率和面积因数都与等应力杆相等的阶梯形和圆锥形变幅杆,以及固有频率与之相同的等截面变幅杆。图5所示为四种不同形状变幅杆轮廓曲线。

图4 (a)应力云图 (b)变幅杆应力分布曲线

图5 四种形状变幅杆轮廓曲线
对于相同材料和相同固有频率的变幅杆,形状因数φ是衡量其能达到最大振幅的标准,其表达式如下:
(8)
其中:ξmax为变幅杆输出端的速度,σmax为发生在变幅杆上的最大应力,ρC为变幅杆的材料机械阻抗,它仅与材料有关。为了计算方便,本文引入了一个参数τ,其与φ满足如下关系:
φ=2πfρC·τ
(9)

对于同一材料的变幅杆,τ值与变幅杆的形状因数成正比,单位为m/Pa。它的物理意义是:变幅杆上的最大应力每增加1 Pa,变幅杆振幅所增加的量。通过比较τ值来衡量不同形状变幅杆能达到最大振幅,只需要δmax和σmax两个量,这两个量在ANSYS谐响应分析中都可以获得。值得注意的是,ANSYS谐响应分析时,输入的阻尼值会对δmax和σmax两个量计算结果有很大影响,但是对其比值即τ值没有影响,因此可以设置阻尼为一个经验值(如α=113.087,β=9.19×10-10)。表6所示为四种变幅杆ANSYS谐响应分析计算后所得的各个参数值。
由表6可知,在同一电压激励下(1Vp-p),虽然阶梯形变幅杆振幅最大,但是应力也远远大于其他三种变幅杆,所以当激励电压增加时,它会最先断裂。等应力变幅杆的τ值最大,为0.371×10-12m/Pa,高于圆锥形变幅杆(τ为0.257×10-12m/Pa)44.4%,所以当激励电压不断增大,它能获得的振幅最大而最后断裂。等截面变幅杆由于对振子输出端振幅没有放大作用,所以在相同大小的激励电压下,它的振幅最小,但是随着电压的增大,当发生断裂时,它能达到的振幅却约为阶梯形变幅杆的2倍。

表6 不同形状变幅杆谐响应分析结果
3 实验测试
在数值模拟的基础上,加工了用前述方法设计的等应力变幅杆,图6所示为包括郎之万振子和等应力变幅杆的换能器装配实物图。

图6 超声换能器系统
在小信号(1Vp-p)激励下,用LCR-8081精密阻抗仪测量获得了换能器振动系统的导纳和相位曲线(分析频率范围为50~60 kHz)如图7所示。其谐振频率为56.083 kHz,这与ANSYS数值计算所得结果(55.735 kHz)相差0.61%。在分析频率范围内只有一个谐振峰,这也有利于抑制系统其它振型对所需振型的干扰。
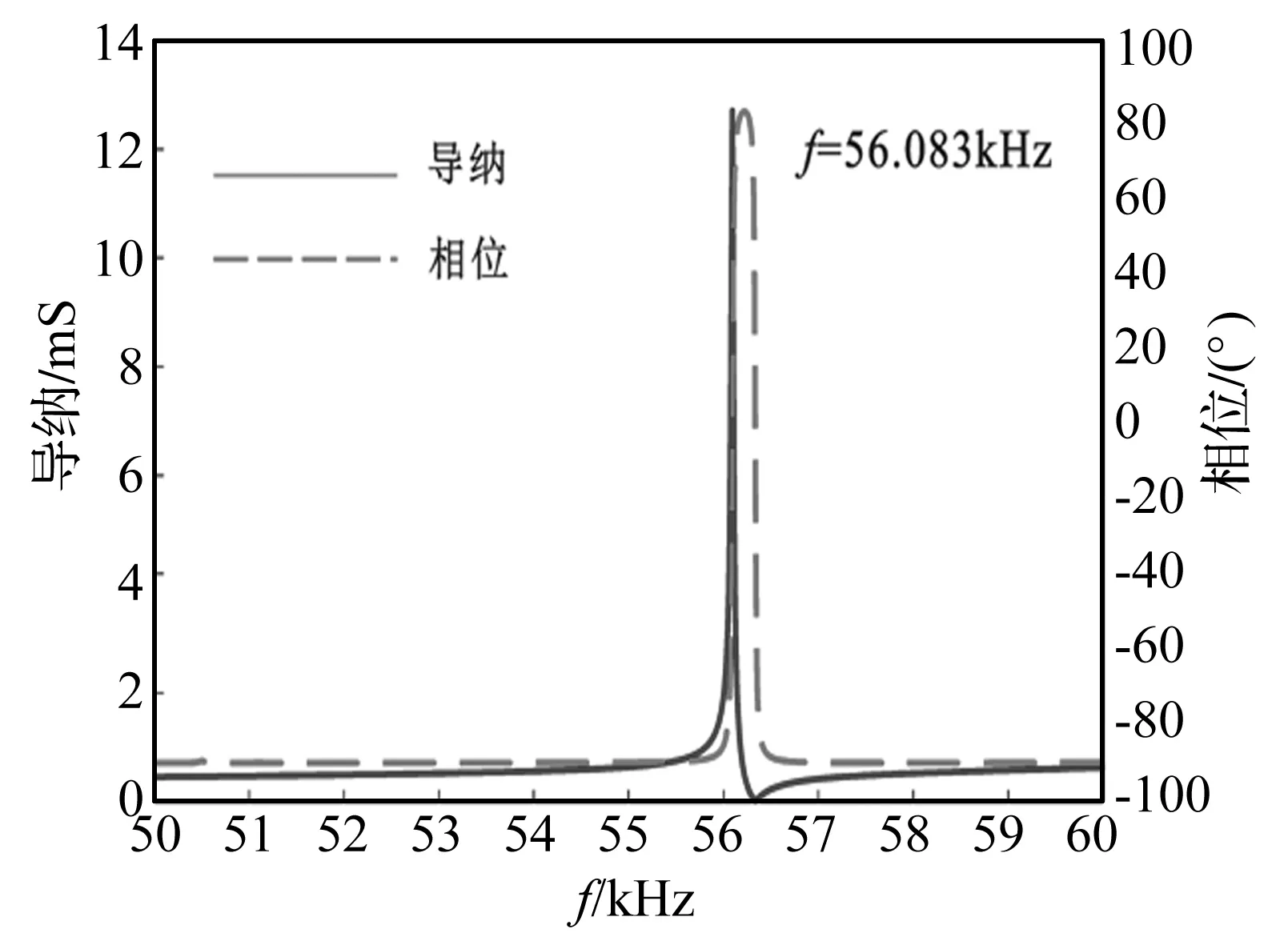
图7 导纳和相位曲线
由于振幅超过10 μm,可以用长焦距显微镜在振动端面上直接观测振幅,测量装置示意图如图8。信号发生器(RIGOL DG1022)输出正弦信号经功率放大器(LM3886)接入振子,调节信号频率并利用数字示波器(Rigol DS 5022)观察输入振子电压信号,使超声换能器工作在共振状态。通过显微镜数码摄像机(DCM136)将变幅杆输出端的振动图像传输到电脑。经软件(ScopePhoto3.0)标定变幅杆上一点并测量振幅大小如图9所示,由图可知,变幅杆的振幅都随着电压的增大而增大。相同激励电压下,等应力变幅杆振幅约为等截面形状杆的5.23倍。当电压为198Vp-p时,振幅峰峰值达到148 μm,此时超声变幅杆的响应频率为55.9 kHz。试验中,随着电压的增大和工作时间的持续,变幅杆振幅的增大速度会变小且响应频率也会变小。通过分析,这种现象是由于随着激励电压的增大和工作时间的持续会引起材料发热,温度的升高导致材料特性变化而引起的。
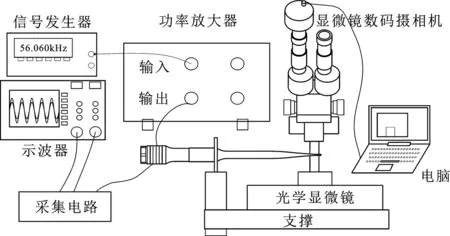
图8 变幅杆振幅测试装置
图10所示为激励电压分别为80、90和100Vp-p时所测变幅杆频率响应曲线。由图可知,响应频率随着电压的增大而减小。在实际工作中,随着负载的变化,变幅杆的响应频率也会发生一定的变化,可利用锁相环技术跟踪频率解决这个问题。

图9 振幅-电压关系
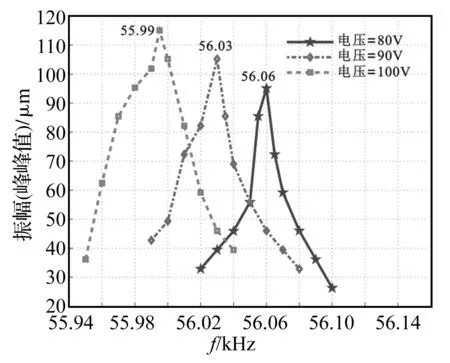
图10 三种激励电压变幅杆频率响应曲线
4 结 论
在深入研究超声变幅杆振动的基础上,从提高变幅杆形状因数的角度,通过理论计算和ANSYS软件仿真结合的方法,设计了应力沿杆均匀分布的超声变幅杆。这种形状的变幅杆在同一材料和同一频率的条件下,理论上能获得最大的振动幅值。这种变幅杆的形状有两个特点:第一,发生在杆上最后1/4波长大部分长度上的应力相等;第二,应力分布均匀处的应力也是变幅杆上应力最大值处。
加工和测试了郎之万振子和等应力变幅杆,实测频率与理论计算频率十分接近。通过对所设计的超声变幅杆实验测试可知,当激励电压为198Vp-p时,变幅杆的振幅峰峰值可达到148 μm。远大于现有的同频率下变幅杆的振幅。研究结果将在超声焊接、超声马达和超声液体泵等领域中具有广泛的应用。但是本系统在实际应用中还存在一些不足,尚需改进:随着激励电压的提高和工作时间的增加,材料性质非线性越来越显著,变幅杆的发热问题也越来越突出,这不利于工作的稳定性和安全性。所以还需要设计散热系统等,以抑制温度提高引起的一系列问题。
[1]谢欣平,田阿利,王自力,等.考虑负载影响的阶梯形超声变幅杆动力特性[J].振动与冲击,2006,25(1):82-86.
XIE Xin-ping,TIAN A-li,WANG Zi-li,et al.Dynamic performance of ultrasinic stepped horn with consideration of loading effect[J].Journal of Vibration and Shock,2006,25(1):82-86.
[2]Bangviwat A,Ponnekanti H K,Finch R D.Optimizing the performance of piezoelectric drivers that use stepped horns[J].The Journal of the Acoustical Society of America,1991,90: 1223.
[3]Sindayihebura D,Bolle L,Cornet A,et al.Theoretical and experimental study of transducers aimed at low-frequency ultrasonic atomization of liquids[J].The Journal of the Acoustical Society of America,1998,103: 1442.
[4]Eisner E.Design of sonic amplitude transformers for high magnification[J].The Journal of the Acoustical Society of America,1963,35: 1367.
[5]Crouch D D,Dolash W E.Dual-window high-power conical horn antennaa[P].U.S.Patent 6211837.2001-4-3.
[6]Graff K F.Wave motion in elastic solids[M].Courier Dover Publications,1975:116.
[7]Wang D A,Chuang W Y,Hsu K,et al.Design of a Bézier-profile horn for high displacement amplification[J].Ultrasonics,2011,51(2): 1 48-156.
[8]林仲茂.超声变幅杆的原理与设计[M].北京:科学出版社,1987:241.
