关于箱型梁结构提高舰船抗舱内爆炸可靠性水平的研究

于海洋，张世联，武少波，乔 迟

(上海交通大学 船舶海洋与建筑工程学院，上海 200240)

在现代海战中，各种半穿甲反舰导弹能够轻易地击穿舷侧板架，侵入舰船内部，在舱内爆炸，对舰船造成致命打击[2]。舰船在舱内爆炸载荷下的结构可靠性是评价舰船生命力的重要指标，如何提高舰船在舱内爆炸载荷下的可靠性是一个值得深入研究的课题。

研究表明，在舰船强力甲板上设置纵向箱型梁结构，能有效提高舰船在舱内爆炸冲击载荷下的防护能力[1]。不过目前的研究主要是确定性分析，而实际上舰船在内部爆炸载荷作用下的变形和破损过程中，许多参数通常都是不确定量，因此，还应该考虑破坏概率，即结构可靠性的问题。

在不确定性分析方面，国内学者就水下爆炸载荷下多层板壳的破坏概率[4]、战斗部撞击下加筋板架破坏概率[5]和水下爆炸载荷下舰船舷侧防护结构可靠性[6]等问题进行了研究。但完整舰船舱段结构在内部爆炸载荷作用下的破坏概率研究尚未见报道。

本文针对设置箱型梁结构舰船和普通结构舰船的完整舱段，选取钢材弹性模量，钢材极限强度和TNT装药密度以及炸点位置作为随机变量，分别计算结构在舱内爆炸载荷作用下的破坏概率，通过比较分析，进而评估箱型梁结构提高舰船抗舱内爆炸可靠性的水平。结构可靠性分析采用Monte-Carlo方法，选取稳定后的01甲板变形和等效塑性应变作为评价指标，根据最大熵法编写程序拟合结果概率分布。结构在舱内爆炸载荷作用下的响应非常复杂，而且需要考虑流固耦合的影响，因此借助FEM法进行数值计算。本文所使用的数值分析软件是MSC-Dytran。

1 随机变量的选取

同时，考虑到装药在舱内爆炸位置的随机性，选取炸点位置Z作为随机变量。为了控制样本数量，对该变量进行了适当简化，将炸点位置限制在01甲板和1甲板之间，且位于船体中横剖面的对称轴上，仅Z向坐标变化。根据实际情况，认为Z符合均匀分布。在本文计算模型中，Z～U(10 500,12 100)，单位为mm。

表1 各正态分布随机变量的均值和方差

以上各组随机变量(E,R,ρ,Z)直接采用Matlab中的随机数生成函数得到，共100组。

2 舱段有限元模型

2.1 计算模型的选取

选取在01甲板设置箱型梁结构的某型舰的三个完整舱段进行计算，中间舱段为舱室内部爆炸处理数值仿真的目标舱段，模型两端使用多点约束。该处理方法能够更准确的模拟舱段之间的支撑关系，减小以往单舱段模型两端约束过强对仿真计算带来的影响。为了对箱型梁结构提高舰船抗爆可靠性水平进行评估，另外设置一个普通结构舱段模型作比较。普通舱段01甲板未设置箱型梁结构，代之以甲板纵桁，其余部分与箱型梁结构舱段基本相同。两种结构的横剖面比较如图1所示。

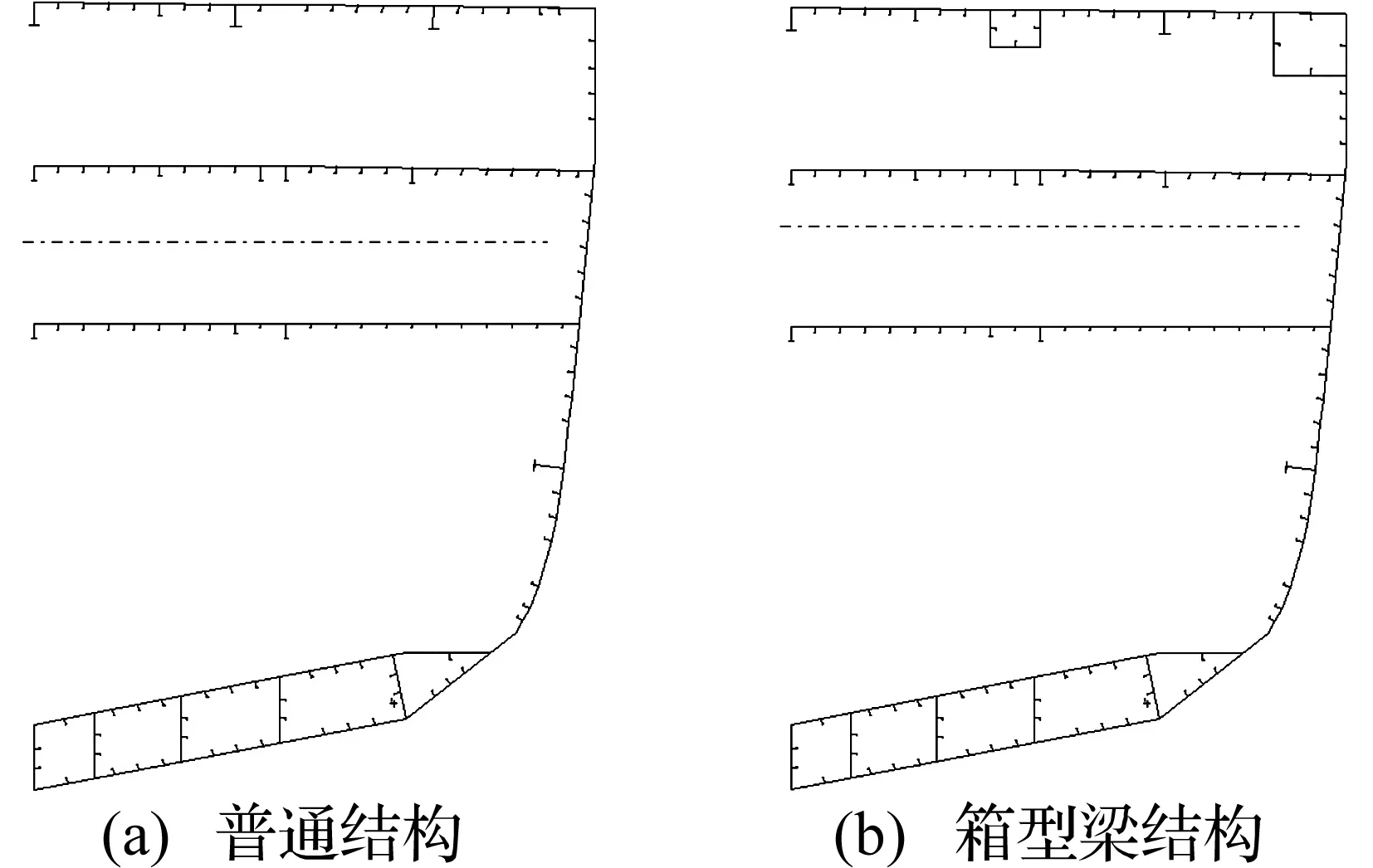
图1 舱段横剖面示意图

考虑到设置箱型梁所带来的重量增加，为了能够比较，文中在常规结构模型的基础上对01甲板、1甲板以及它们之间的舷侧结构进行了适当的加强，加强后横剖面特征参数与箱型梁结构型式基本一致，称为普通结构。两种结构的剖面特性如表2所示。

对两种结构形式的舱段分别进行有限元建模，模型如图2所示。

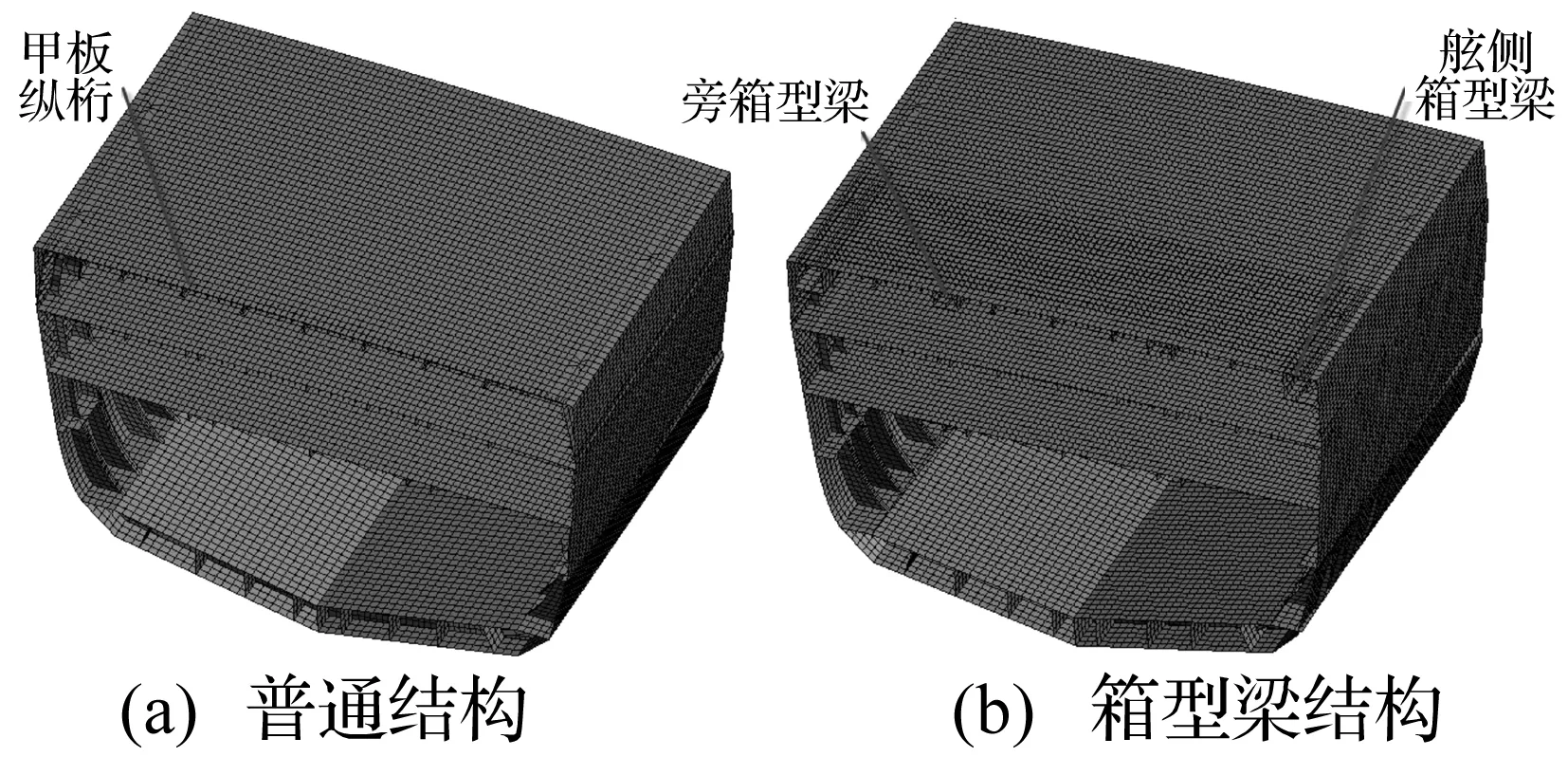
图2 舱段有限元计算模型

表2 舱段结构剖面特性表

在所选舱段的01甲板上布置测点，测点布置情况见表3和图3，其中测点1位于甲板正中。计算结构在舱内爆炸载荷下的响应。当测点的塑性应变大于某个值时，则认为结构失效。

表3 01甲板上的测点位置数据

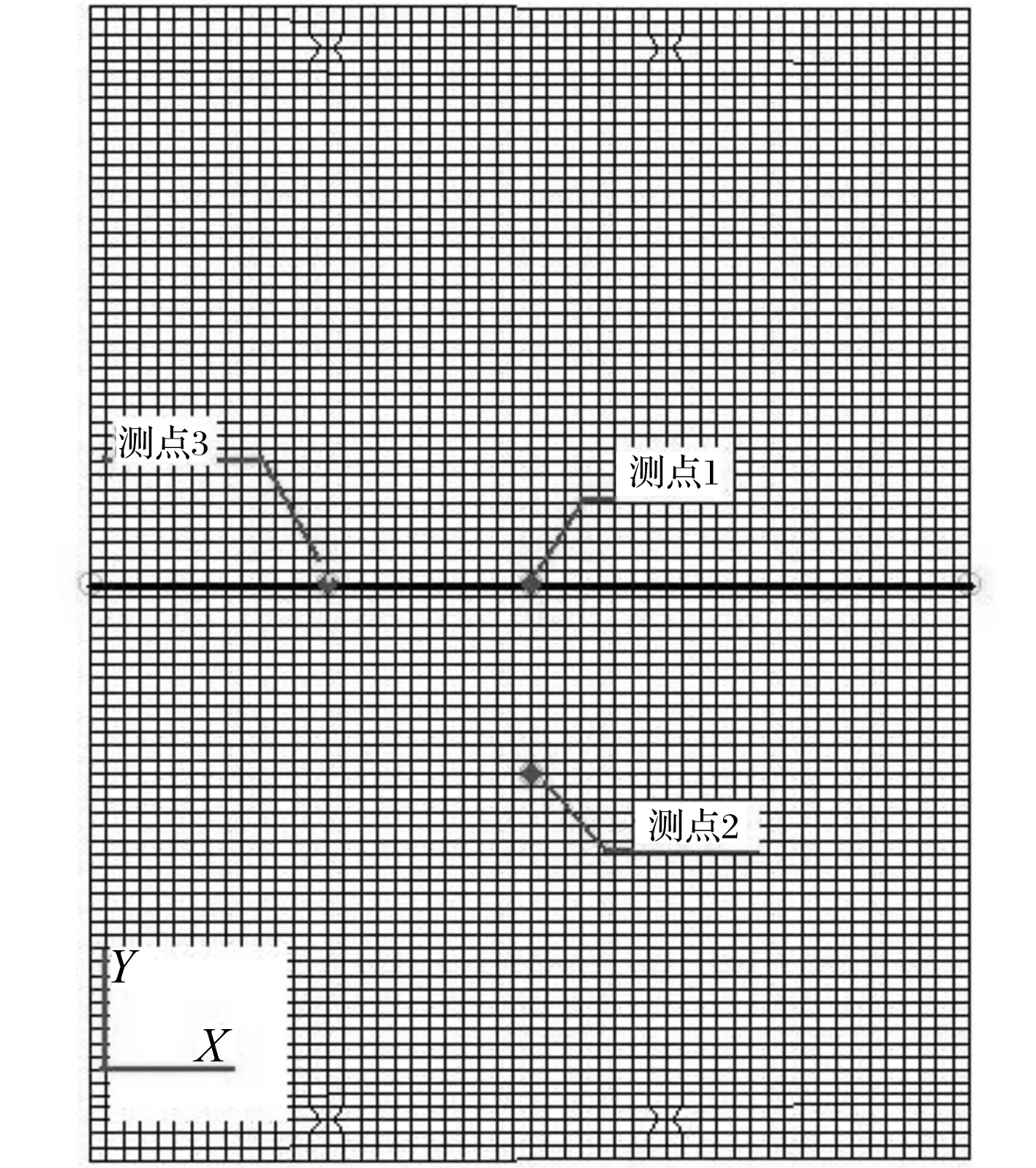
图3 01甲板测点布置示意图

2.2 本构关系和状态方程

对随机生成的100个样本，本文利用MSC-Dytran软件中的流固耦合算法来逐一模拟装药对舰船舱段结构的破坏作用，采用能够考虑耦合面破坏的快速耦合算法与Euler求解器求解。

材料采用能考虑动态应变率效应的Cowper-Symonds模型描述[3]，其本构方程

(1)

同时，应力-应变关系近似的模拟为双线性弹塑性材料，从而考虑了应变强化效应，如下式所示：

(2)

式中:σy为屈服应力；σ0为初始屈服极限，E为弹性模量，这两个值取为正态分布随机变量，均值分别为440 Mpa和2.07×105Mpa；Eh为硬化模量，取为4 Gpa；Εh为等效塑性应变，本文中最大等效塑性应变取为0.18；泊松比取为0.3。

舱室内外空气采用理想气体状态方程描述，即Gamma方程

p=(γ-1)·ρ·e

(3)

式中:比热比γ=1.4、空气密度ρ=1.25 kg/m3、空气比内能e=2.1×105J/kg。

TNT炸药用高能高压的空气来模拟，同样采用Gamma方程，其中炸药密度取为正态分布随机变量，均值为ρd=1 630 kg/m3，炸药比内能ed=4.2×106J/kg。本文采用球形装药，炸药半径取为0.280 m，故装药量的均值约为150 kg TNT。

2.3 典型工况下结构响应数据

本文生成100组随机变量(E,R,ρ,Z)，对每组变量所对应的工况，分别对设置箱型梁结构和普通结构进行了数值仿真计算。现取一个工况，给出该工况下箱型梁结构01甲板的典型响应数据。

所取的工况为，E=2.01×105MPa，R=441 Mpa，ρ=1 585.07 kg/m3，Z=11 629 mm。在此工况下各测点的响应值如表4所示，01甲板的变形情况如图4所示。

表4 典型工况下箱型梁结构的01甲板响应值

表中d和e分别代表塑性变形与等效塑性应变，下标表示测点编号。

图4 典型工况下箱型梁结构的01甲板变形云图

从表4中可知，三个测点都产生了明显变形，测点1的等效塑性应变较大，而测点2、3的等效塑性应变很小，其它工况也具有类似的规律。下文着重对测点1处的等效塑性应变和测点2、3处的变形(节点位移)进行了讨论。

3 舱段在内部爆炸载荷下的破坏概率

对于仿真计算结果，首先采用D’Agostino检验方法来检验结果是否服从正态分布[8]。D’Agostino检验方法要求的样本个数为50～1000，故本文的样本个数100适用于该检验。对于给定的置信度α=0.05和样本容量n=100，从所定义统计量的α=0.05分位表中查得Za/2=Z0.25=-2.54，Z1-a/2=Z0.975=1.31；本文基于Matlab软件编写了用D’Agostino方法检验正态分布的程序。

若数值计算得到的结果经过D’Agostino检验不符合正态分布，则采用最大熵法拟合结果概率密度函数[5][7]，进而求得破坏概率。本文基于Matlab软件编写了最大熵法计算程序，对数值计算得到的结果数据，取前四阶矩，可以得到结果样本的概率密度函数。

本文着重考察了01甲板的响应。

3.1 结构在测点1的等效塑性应变

利用MSC-Dytran计算得到测点1处的等效塑性应变，作出频率分布直方图，如图5所示，进而算得其均值和标准差的估计值如下:

μ1eff1=0.053 9σ1eff1=0.060 2

μ2eff1=0.047 9σ2eff1=0.059 6

其中:μ1eff1、σ1eff1和μ2eff1、σ2eff1分别表示设置箱型梁结构和普通结构在测点1处等效塑性应变的均值与标准差。

经D’Agostino检验方法检验，认为对于置信度α=0.05，两组结果均不符合正态分布，故采用最大熵法对结果数据进行拟合。最大熵法计算得到的概率密度曲线如图6所示。

对于等效塑性应变γeff，本文中认为当γeff≥0.18时01甲板将产生破口，当γeff≥0.14时01甲板区域将产生大的塑性变形。由此可得，对于设置箱型梁舱段结构，内部爆炸载荷下01甲板产生破口的概率为

01甲板中部(炸点正上方)产生大的塑性变形的概率为

对于普通结构舱段，内部爆炸载荷下01甲板产生破口的概率为

01甲板中部(炸点正上方)产生大的塑性变形的概率为

由此可见，与普通结构相比，箱型梁结构未能减小内部爆炸载荷下01甲板产生破口的概率，对于减小炸点正上方区域发生塑性大变形的概率的作用也并不明显。但是应该注意到，为了实现重量与设置箱型梁结构舱段大致相等，对普通结构舱段的01甲板进行了约2 mm的加厚处理，这说明设置箱型梁结构舱段在01甲板板厚明显较小的条件下达到了类似的抗爆性能，这也是设置箱型梁结构01甲板产生破口概率略大于普通结构的原因。

另外，通过对比图5和图6可以看出，采用最大熵法得到的概率密度曲线能够很好地模拟计算结果的频率分布情况，因此认为通过该方法算得的损伤概率具有较高的参考价值。

图5 测点1处等效塑性应变(eff1)的频率分布直方图

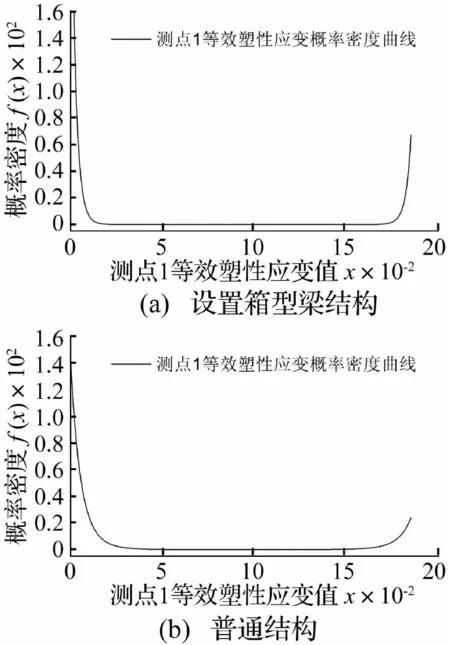
图6 最大熵法算得测点1等效塑性应变的概率密度曲线

图7 测点2处节点位移(dis2)的频率分布直方图

3.2 结构在测点2的变形

利用MSC-Dytran计算得到测点2处的节点位移(变形)，作出频率分布直方图，如图7所示，进而算得其均值和标准差的估计值如下:

μ1dis2=462.325σ1dis2=24.210

μ2dis2=559.683σ2dis2=16.535

其中:μ1dis2、σ1dis2和μ2dis2、σ2dis2分别表示设置箱型梁结构和普通结构在测点2处节点位移的均值与标准差，位移单位为mm。

经D’Agostino检验方法检验，认为对于置信度α=0.05，两组结果均符合正态分布。直接按照正态分布进行计算得到，对设置箱型梁结构舱段，测点2处的变形大于550 mm的概率为

对普通结构舱段，测点2处的变形大于550 mm的概率为

由此可见，箱型梁结构可以明显减小内部爆炸载荷下01甲板发生横向大变形的概率。这是因为旁箱型梁对01甲板区域起到了有效的支持作用，从而限制了横向变形的扩散。

3.3 结构在测点3的变形

利用MSC-Dytran计算得到测点3处的节点位移(变形)，作出频率分布直方图，如图8所示，进而算得其均值和标准差的估计值如下:

μ1dis3=392.143σ1dis3=21.217

μ2dis3=444.695σ2dis3=14.740

其中:μ1dis3、σ1dis3和μ2dis3、σ2dis3分别表示设置箱型梁结构和等重量普通结构在测点3处节点位移的均值与标准差，位移单位为mm。

经D’Agostino检验方法检验，认为对于置信度α=0.05，设置箱型梁结构的计算结果符合正态分布，而普通结构的计算结果则不符合正态分布。故对于设置箱型梁结构舱段，可以直接按照正态分布进行计算得到，测点3处的变形大于450 mm的概率为

而对普通结构舱段，则需要通过最大熵法拟合计算结果后才能算得相应概率。

最大熵法计算得到的概率密度函数曲线如图9所示。

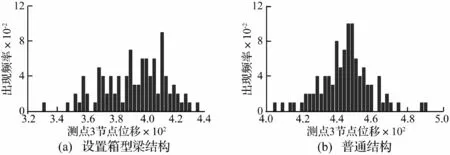
图8 测点3处节点位移(dis3)的频率分布直方图

图9 最大熵法算得普通结构测点3处节点位移的概率密度曲线

对普通结构舱段，测点3处的变形大于450 mm的概率为

由此可见，箱型梁结构可以明显减小内部爆炸载荷下01甲板发生纵向大变形的概率。这是因为旁箱型梁及舷侧箱型梁结构将甲板结构分隔为较窄的区段，并能在区段边缘提供有力的支持和约束，从而有效减小了01甲板的纵向动态响应。

本章从不确定性分析的角度定量地评价了箱型梁结构对提高舰船抗舱内爆炸可靠度的贡献。分析发现其对降低炸点正上方区域产生塑性大变形的概率有一定作用，对抑制变形区域的扩散有显著效果，这使01甲板结构在承受舱内爆炸载荷作用后拥有比普通结构更大的有效承载区域，从而大幅度提高舰船生命力。值得注意的是，这些优势是在结构重量和横剖面特性没有显著增加的情况下得到。这些结论与传统确定性分析所得到的结果有相似之处，这在一定程度上证明了本文可靠性分析结果的参考价值。

4 结 论

本文基于MSC.Dytran分析软件，模拟两种结构舰船舱段在舱内爆炸载荷下的响应，并应用可靠性理论对结构破损概率进行分析和比较，得到了关于箱型梁结构提高舰船抗舱内爆炸可靠性水平的一些结论，现归纳如下：

(1)与普通结构相比，箱型梁结构对于减小内部爆炸载荷下01甲板产生破口的概率和炸点正上方区域发生塑性大变形的概率作用并不明显。

(2)应该注意到，设置箱型梁结构舱段的01甲板厚度比普通结构的01甲板厚度要小2 mm左右，这说明在炸点附近区域，设置箱型梁结构舱段在01甲板板厚较小的条件下达到了类似普通结构的抗爆性能。

(3)在不显著增加横剖面特性和结构重量的情况下，设置箱型梁结构可以明显减小舱内爆炸载荷下01甲板产生横向和纵向大变形的概率，从而使其具有更大的有效承载面积，这对于提高舰船的剩余极限强度有着重要意义。因此箱型梁结构可以有效提高舰船在舱内爆炸下的生存能力。

本文的参数分布和取值都是估计得出的，可能与实际情况有出入；进行结果数据拟合的最大熵法虽然已经在工程中广泛运用，但我们目前仍无法从数学原理上了解最大熵法的可靠度计算精度，这些都是未来需要解决的问题。另外，研究表明，箱型梁结构对舰船抗爆能力的提升，在很大程度上还表现在其对舰船遭遇舱内爆炸后剩余极限强度的提升上，这一问题有待进一步研究。

[1]王佳颖，张世联，彭大炜.非接触爆炸下纵向箱型梁舰船的极限承载能力研究[J].中国舰船研究，2011，6(1): 22-29.

WANG Jia-ying，ZHANG Shi-lian，PENG Da-wei.Ultimate bearing capacity analysis of longitudinal box girder of warship under non-contact explosion[J].Chinese Journal of Ship Research，2011，6(1): 22-29.

[2]魏继锋，戴文喜，徐豫新，等.反舰导弹对舰船侵彻及内爆毁伤研究[J].振动与冲击,2012,31(20):162-165.

WEI Ji-feng，DAI Wen-xi，XU Yu-xin，et al.Anti-warship missile penetrating to a warship and ship's inner-explosion damage[J].Journal of Vibration and Shock，2012，31(20): 162-165.

[3]李聪，张世联，刘慧泉，等.迎爆加强筋耦合程度及简化建模方式的研究[J].振动与冲击，2012,31(23): 12-15.

LI Cong，ZHANG Shi-lian，LIU Hui-quan，et al.Coupling level of stiffeners facing blast load and its simplified modeling methods[J].Journal of Vibration and Shock，2012，31(23): 12-15.

[4]施兴华，张婧，王善.水下接触爆炸载荷作用下多层板壳破坏概率分析[J].弹道学报，2009，21(1): 1-4.

SHI Xing-hua，ZHANG Jing，WANG Shan.Destroy probability of multilayer plate-shell structure subjected to underwater contact explosions[J].Journal of Ballistics，2009，21(1)，1-4.

[5]何建，欧阳志为，王善，等.冲击载荷作用下加筋板架破坏概率分析[J].应用力学学报，2006，23(4): 583-586.

HE Jian，OUYANG Zhi-wei，WANG Shan，et al.Destroy probability analysis of stiffened plate under impact load[J].Journal of Applied Mechanics，2006，23(4): 583-586.

[6]Zhang J，Shi X H，Xu D H，et al.Destroy probability of ship defensive structure subjected to underwater contact explosions[J].Advanced Materials Research，2008，44-46:297-302.

[7]韦征，叶继红，沈世钊.最大熵法可靠度理论在工程中的应用[J].振动与冲击，2007，26(6): 146-151.

WEI Zheng，YE Ji-hong，SHEN Shi-zhao.The application of maximum entropy reliability theory in engineering[J].Journal of Vibration and Shock，2007，26(6): 146-151.

[8]何建，金波.爆炸作用下单层板失效概率[J].低温建筑技术，2008，5(2): 49-50.

HE Jian，JIN Bo.Destroy probability of single plate under explosion[J].Low Temperature Architecture Technology，2008，5(2): 49-50.

[9]谢政，李建平，陈挚.非线性最优化理论与方法[M].北京：高等教育出版社，2010.