食饵具有阶段结构的时滞捕食系统的Hopf分支控制

刘 娟， 孙礼俊

(蚌埠学院 数学与物理系,安徽 蚌埠 233030)

0 引言

捕食系统在种群动力学建模中非常重要,多年来受到国内外许多学者的关注[1-3]．但是,在传统的捕食系统模型中,都假设食饵对捕食者的威胁具有相同的抵御能力．这种假设对于许多动物种群来说是很不现实的．因此,近年来具有阶段结构的捕食系统模型受到学者的关注[4-9]．文献[6]研究了一类食饵具有阶段结构的时滞捕食系统模型

(1)

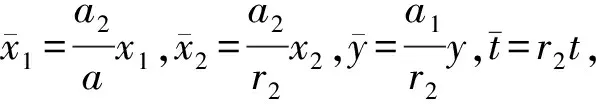
(2)

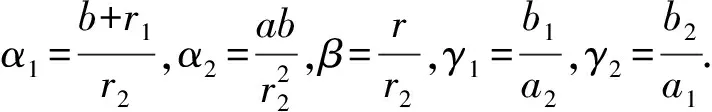
文献[6]研究了系统(2)的Hopf分支问题,得到了系统(2)产生Hopf分支的充分条件．Hopf分支是一种重要的非线性现象,而这种现象的发生可能对动力系统造成难以估计的有害影响．基于此,本文针对系统(2),利用状态反馈和参数扰动设计Hopf分支控制器,研究受控系统的Hopf分支,其模型如下：

(3)

其中α′和β′是对系统Hopf分支进行控制的参数．

1 受控系统的Hopf分支存在性

显然,系统(3)和(2)具有相同的平衡点．由文献[6]知,如果系统(3)满足条件

H1)α2-(1+βγ1)α1>0,

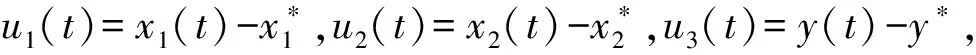
(4)

系统(4)的特征方程为

λ3+A2λ2+A1λ+A0+(B2λ2+B1λ+B0)e-λτ+(C1λ+C0)e-2λτ=0,

(5)

其中

A0=(a12a21-a11a22)a33,A1=a11a22-a12a21+(a11+a22)a33,A2=-(a11+a22+a33),

B0=a11(a23b32-a33b22)+b33(a12a21-a11a22),B1=b22(a11+a33)+b33(a11+a22)-a23b32,

B2=-(b22+b33),C1=b22b33,C0=a11b22b33.

方程(5)两边同时乘以eλτ,得到

B2λ2+B1λ+B0+(λ3+A2λ2+A1λ+A0)eλτ+(C1λ+C0)e-λτ=0,

(6)

当τ=0时,方程(6)变为

λ3+(A2+B2)λ2+(A1+B1+C1)λ+A0+B0+C0=0.

(7)

根据赫尔维茨定理,如果

H2)A2+B2>0,且(A2+B2)(A1+B1+C1)>A0+B0+C0,

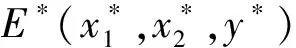
当τ>0时,令λ=iω(ω>0)为特征方程(6)的根,代入(6)并分离实虚部得

(8)

从而,有

(9)

其中

n5=B2,n3=A2B1-A1B2-B2C1-B0,n1=A1B0+B0C1-A0B1-B1C0,

n4=B1-A2B2,n2=(A0-C0)B2+(C1-A1)B1+A2B0,n0=B0(C0-A0),

进而,得到

ω12+e5ω10+e4ω8+e3ω6+e2ω4+e1ω2+e0=0,

(10)

其中

令ω2=v,方程(10)变为

v6+e5v5+e4v4+e3v3+e2v2+e1v+e0=0.

(11)

下面给出如下假设:

H3) 方程(11)存在6个正根,分别表示为v1,v2,v3,v4,v5和v6,

对于每个特定的ωk,根据(9),可以得到

方程(6)的两端分别对τ进行求导,得到

因此

其中

显然,如果

H4)PRQR+PIQI≠0,

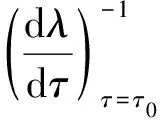
根据文献[9]中的Hopf分支定理,得到下列结果．

定理1对于受控系统(3),如果H1)～H4)成立,则

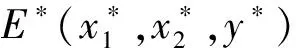
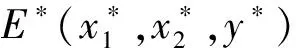
2 数值模拟

对受控系统(3)进行数值模拟,系统参数选取如下:

α1=0.5,α2=2,β=1,γ1=0.25,γ2=0.5,α′=0.2,β′=0.4.

得到受控系统

(12)

图1 当τ=4.5<τ0=4.6375时,系统(12)渐近稳定

图2 当τ=4.75>τ0=4.6375时,系统(12)不稳定并发生Hopf分支

3 结论

Hopf分支控制是通过对给定的非线性动力系统设计一个控制器,用来延迟或者消除Hopf分支的产生，从而去掉系统中的有害动力学性质．本文针对一类食饵具有阶段结构的时滞捕食系统,设计了一类Hopf分支控制器，并通过分析受控系统特征方程根的分布,给出受控系统Hopf分支存在的充分性条件．最后,利用仿真实例,验证了所设计的控制器的有效性．

参考文献:

[1] 郑重武,张凤琴.一类捕食者有病的捕食-被捕食的SIS模型[J].徐州师范大学学报:自然科学版,2008,26(2):132.

[2] 韩二东,郑唯唯,罗立贵.一类两种群均有收获率捕食系统的细焦点与极限环[J].生物数学学报,2008,27(3):447.

[3] 姜乐,吴强,吕小光.一类依赖比率的Holling-Tanner捕食模型的定性分析[J].徐州师范大学学报:自然科学版,2007,25(3):19.

[4] 刘娟.具有时滞和阶段结构的捕食系统的分支分析[J].北华大学学报:自然科学版,2014,15(2):149.

[5] 刘娟,张子振.具有阶段结构的时滞Crowley-Martin功能反应型捕食者-食饵系统的Hopf分支[J].应用数学,2014,27(1):88.

[6] Wang Lingshu,Xu Rui,Feng Guanghui.A stage-structured predator-prey system with time delay[J].J Appl Math Comput,2010,33(1):267.

[7] Kar T K,Janna Soovoojeet.Stability and bifurcation analysis of a stage structured predator prey model with time delay[J].Appl Math Comput,2012,219(8):3779.

[8] Xu Rui.Global dynamics of a predator-prey model with time delay and stage structure for the prey[J].Nonlinear Anal RWA,2011,12(4):2151.

[9] Sun Xiaoke,Huo Haifeng,Xiang Hong.Bifurcation and stability analysis in predator prey model with a stage-structure for predator[J].Nonlinear Dyn,2009,58(3):497.

[10] Hassard B D,Kazarinoff N D.Theory and applications of Hopf bifurcation[M].Cambridge:Camb Univ Press,1981.