Klein-Gordon-Schrödinger耦合方程的线性化紧致差分格式

孙启航, 徐尚巧

(鲁东大学 信息与电气工程学院,山东 烟台 264025)

0 引言

在量子场论中,非线性Klein-Gordon-Schrödinger(KGS)耦合方程刻画了守恒复中子场和中性介子场Yukawa相互作用的经典模型[1-2]．许多作者从解的性质、类型以及数值解法等方面研究了这类方程[1-6]．文献[5,7-8]中给出了KGS耦合方程的孤立波解、平面波解以及周期解．在数值方面,Xiang[9-10]利用谱方法对此方程进行了研究,并给出了该方法的误差估计．Wang等[11]利用样条配置方法给出了该方程的数值解．Bao等[12]将时间分裂谱离散的方法作用于KGS方程,也得到了较好的数值结果．张鲁明等[13-15]构造了关于KGS方程的守恒差分格式,其收敛阶为O(τ2+h2).本文介绍一个新的紧致差分格式,该格式是线性化的并且解耦的,其收敛阶为O(τ2+h4),并通过理论以及数值试验证明格式的正确性．

考虑如下KGS耦合方程的周期边值问题:

(1)

utt-uxx+u-|φ|2=0,

(2)

φ(x,0)=φ0(x),u(x,0)=u0(x),ut(x,0)=u1(x),

(3)

φ(x,t)=φ(x+L,t),u(x,t)=u(x+L,t), 0≤t≤T,

(4)

其中φ和φ(x,t)是未知的复值函数,u和u(x,t)是未知的实值函数,常数L为方程的周期．

1 预备知识

1.1 符号的定义

为了更方便地解决KGS耦合方程的周期边值问题,定义如下记号:

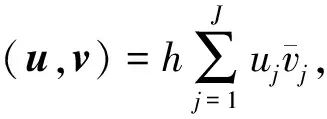
对于所研究的非线性KGS耦合方程的周期边值问题(1)～(4)的精确解,假设

max{‖un‖,‖δxun‖,‖un‖∞}≤C, max{‖φn‖,‖δxφn‖,‖φn‖∞}≤C,

经过简单计算可知,此周期边值问题满足如下守恒性质:

Q(t)=‖φ‖2=Q(0),

(5)

(6)

1.2 几个引理

引理1[16]对任意的网格函数u,v∈Vh,且满足uj=uj+J,vj=vj+J,则有

引理2[16](Gronwall不等式) 假设网格函数{wn|n=0,1,2,…,N;Nτ=T}满足不等式

其中A和Bl(l=0,1,2,…,N)是非负常数,则

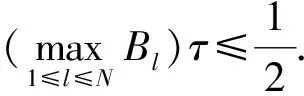
引理3[16]假设网格函数{wn|n=0,1,2,…,N;Nτ=T}满足不等式

wn-wn-1≤Aτwn+Bτwn-1+Cnτ,

其中A,B和Cn(n=0,1,2,…,N)是非负常数,则

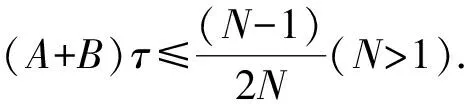
引理4[16]对于序列w={w0,w1,…,wn-1,wn}和g={g0,g1,…,gn-1,gn},有

引理5[16]对任一实值对称正定矩阵HJ×J,un∈Vh,则

其中RJ×J是一个对H进行Cholesky分解得到的上三角实值矩阵,即H=RTR．

引理6[16]对任一实值对称矩阵HJ×J,un∈Vh,则存在两个常数C0和C1,使得

C0‖un‖2≤(Hun,un)≤C1‖un‖2.

引理7[17]对任意的网格函数v∈Vh,有

‖v‖p≤C(‖δxv‖α‖v‖1-α+‖v‖),

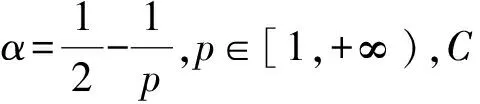
2 KGS耦合方程的线性化紧致差分格式

2.1 格式构造以及离散守恒律

2.1.1 差分格式的构造

对定解问题(1)～(4)提出如下差分格式:

(7)

(8)

(9)

(10)

记

因为M是一个实值对称正定矩阵,因此存在另外一个实值对称正定矩阵H,使得H=M-1,从而格式(7)～(10)可写成如下的向量形式:

(11)

(12)

(13)

(14)

从(11)，(12)式可以得到

(15)

格式(11)是3层的,因此不能自启动．对此可采取其它格式来求解φ1,显然格式(11),(12)是完全解耦的,因此可对φn和Un并行计算,即若已知{φn,Un},可运用格式(11),(12)分别对φn+1,Un+1同时求解,与其它格式相比大大提高了计算速度．

2.1.2 离散守恒律

与(5),(6)对应,所构造的格式具有如下两个离散守恒律:

定理1假设u0∈H1,u1∈L2,φ0∈H1∩L4,格式(11),(12)关于离散质量和离散能量具有如下形式的守恒律:

(16)

=En-1=…=E0.

(17)

证将(11)与φn+1+φn-1作向量内积,然后取虚部得

Ⅰ+Ⅱ+Ⅲ=0

其中

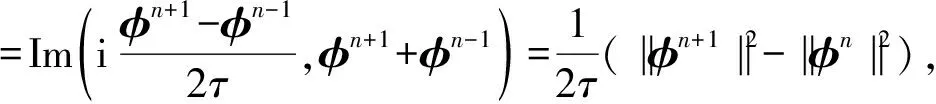
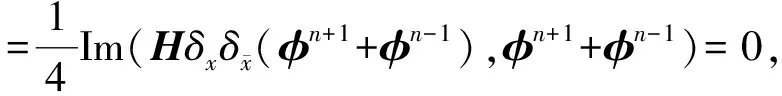
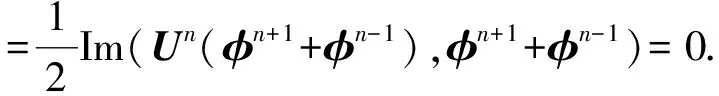
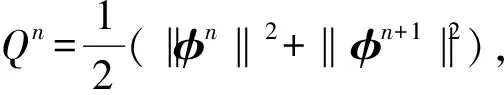
将(11)与φn+1-φn-1作向量内积,然后取实部，再根据引理5，有

(18)

将(12)与Un+1-Un-1作向量内积,再根据引理5,得

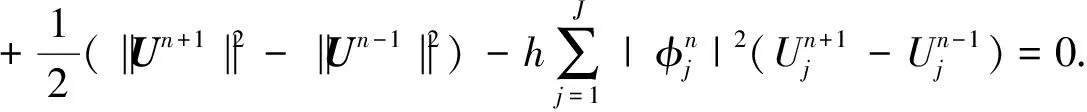
(19)

假设En如(17)所示，则En=En-1=…=E0.

2.2 格式的依最大模范数的收敛性分析

首先,考虑差分格式(11),(12)的截断误差:

(20)

(21)

由(16)式及引理1,6,7,易得如下的先验估计:

引理8(先验估计) 假设u0∈H1,u1∈L2,φ0∈H1∩L4,则格式(11),(12)的差分解满足

‖φn‖∞≤C, ‖Un‖∞≤C.

下面将根据以上结论来证明所构造的差分格式的收敛性.

证令en=φn-φn,ηn=un-Un,0≤n≤N,则有如下误差方程:

(22)

(23)

(24)

(25)

(26)

其中

由引理7,有

将(24)与η1作内积得

‖η1‖∞≤C(τ2+h4).

(27)

将(22)与en+1+en-1作内积,然后取虚部，再根据Cauchy-Schwardz不等式得

钢混凝土叠合梁主梁间桥面板支架通常使用M20型号的弯钩螺杆进行固定，其长度则根据实际测量数据决定，在螺杆上还要再安装双螺母构件。当螺杆的高度基本确定后，要将其与主梁的翼板进行固定焊接，其中纵桥之间的距离控制在1m左右。当这些焊接工作完成后，再需要结合设计图纸的标准，对螺母高度细微调节。

将(23)与δtηn+δtηn-1作内积,利用引理6和Cauchy-Schwardz不等式可得

因此有

≤‖σn‖2+C(‖en‖+‖δtηn‖2+‖δtηn-1‖2).

(28)

由以上可得

≤τ(‖rn‖2+‖σn‖2)+Cτ(‖en+1‖2+‖en-1‖2+‖en‖2+‖δtηn‖2+‖δtηn-1‖2+‖ηn‖2).

(29)

令

(30)

则由(29)得Bn-Bn-1≤τ(‖rn‖2+‖σn‖2)+Cτ(Bn+Bn-1).由引理3,当τ足够小时,有

(31)

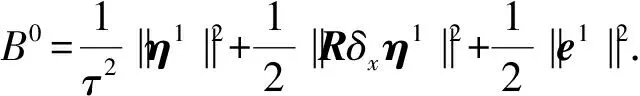
可采取其它具有4阶精度的格式来计算出φ1,则e1也具有4阶精度,故B0≤C(τ2+h4).由引理9,可得

‖en‖≤C(τ2+h4), ‖δtηn‖≤C(τ2+h4), ‖δxηn‖≤C(τ2+h4),

因此得‖ηn‖∞≤C(τ2+h4).

(32)

将(23)与en+1-en-1作内积，然后取实部得

(33)

利用Cauchy-Schwardz不等式可得

≤C(‖en-1‖2+‖en+1‖2+‖ηn‖2+‖Rδxen-1‖2+‖Rδxen+1‖2),

将以上所得代入(33),得

‖Rδxen+1‖2-‖Rδxen-1‖2≤Cτ(‖Rδxen-1‖2+‖Rδxen+1‖2)+Cτ(τ2+h4)2

+τRe(rn,en+1-en)+Cτ(‖en‖2+‖en+1‖2+‖ηn‖2).

对于n,从0连加到k,然后再用n替换k,得

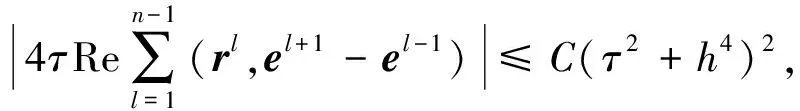
3 数值实验

在数值实验中,当初始条件都有|x|→∞时,|φ0(x)|,u0(x),u1(x)→0,KGS耦合方程有如下的孤立波解[7-8]:

(34)

(35)

这里v是已知的传播速度,x0是初始常数．

取(34)和(35)中的v=0.8,x0=0,h为空间步长．为了验证该格式的收敛阶为O(τ2+h4),选择时间步长τ=h2,x∈[-10,10]以及T=1.格式的误差估计以及收敛阶见表1．可以看出,格式的计算精度接近4阶,此结果也证实了理论分析．

数值方法中最重要的目的之一就是验证问题所满足的守恒律．取h=0.2,τ=0.04,x∈[-10,10]以及T=20. 从图1中可以看出该格式是完全守恒的．图2和图3分别表示孤立波的数值解|φ|,U及精确解φ,u．由此也能看出该格式所求得的数值解和精确解几乎一致,从而也证明了该数值方法的有用性．

表1 差分格式的误差估计和收敛阶

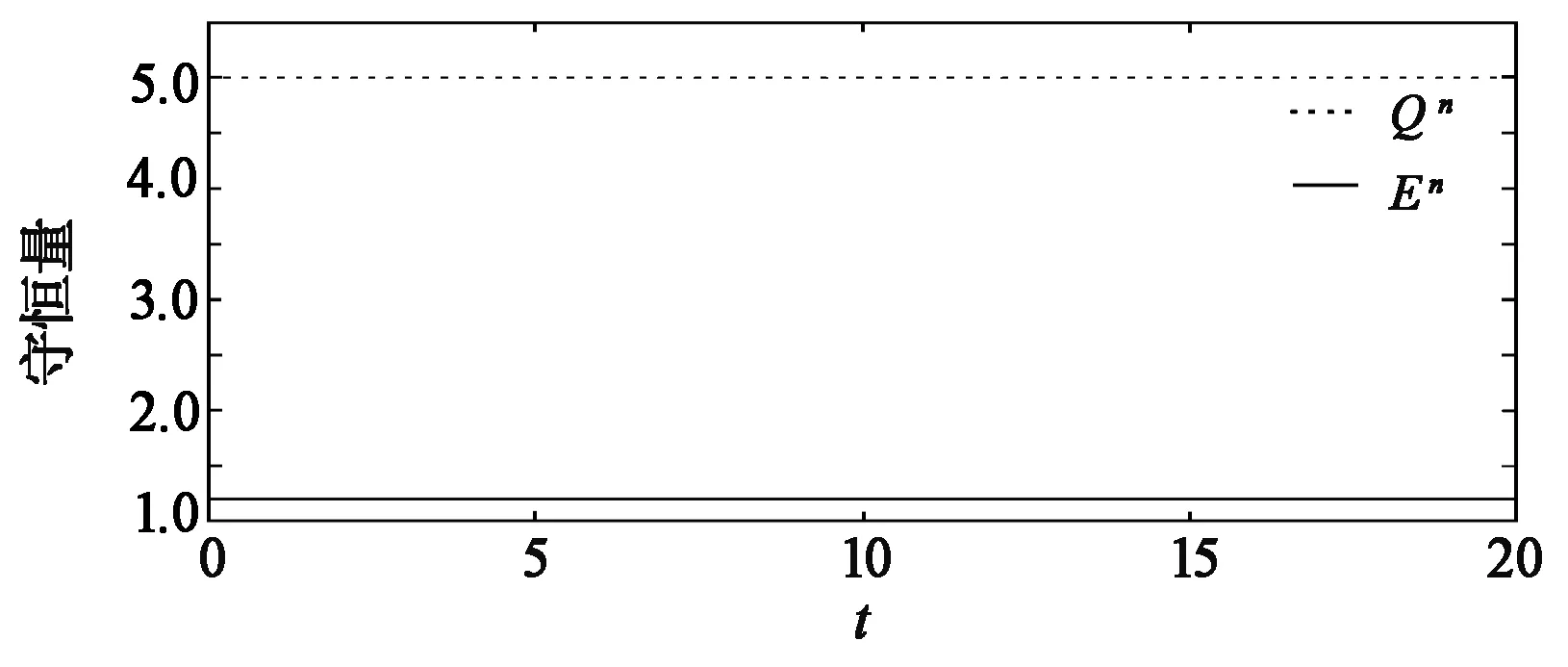
图1 质量和能量守恒量

图2 数值解|φ|与精确解φ的比较

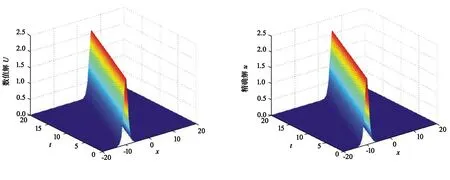
图3 数值解U与精确解u的比较

参考文献:

[1] Makhankov V G.Dynamics of classical solitons(in non-integrable systems)[J].Phys Lett C,1978,35(1):1.

[2] Fukuda I,Tsutsumi M.On coupled Klein-Gordon-Schrödinger equations Ⅱ[J].J Math Anal Appl,1978,66(2):358.

[3] 郭柏灵.复Schrödinger场和实Klein-Gordon场相互作用下一类方程组某些定解问题的整体解[J].中国科学：A辑,1982,2(1):97.

[4] 郭柏灵,苗长兴.Klein-Gordon-Schrödinger 方程解的整体存在性及其渐进性[J].中国科学:A辑,1995,25(7):705.

[5] 夏静娜,韩淑霞,王明亮.Klein-Gordon-Schrödinger方程组的精确孤立波解[J].应用数学和力学,2002,23(1):52.

[6] Ozawa T,Tsutsumi Y.Asymptotic behaviour of solutions for the coupled Klein-Gordon-Schrödinger equations[J].Adv Stud Pure Math，1994,23(1):295.

[7] Xia J,Wang M.Exact solitary solution of coupled Klein-Gordon-Schrödinger equations[J].Appl Math Mech，2002,23(1):58.

[8] Kong Linghua,Liu Ruxun,Xu Zhenli.Numerical simulation of interaction between Schrödinger field and Klein-Gordon field by multisymplectic method[J].Appl Math Comput，2006,181(1):342.

[9] Xiang Xinming.Numerical analysis for a class of equation system in interaction of complex Schrödinger field and real Klein-Gordon field[J].Num Math J Chin Univer,1987,9(1):245.

[10] Xiang Xinming.Spectral method for solving the system of equations of Schrödinger-Klein-Gordon fields[J].J Comput Appl Math,1988,21(2)：161.

[11] Wang Shanshan,Zhang Luming.A class of conservative orthogonal spline collocation schemes for solving coupled Klein-Gordon-Schrödinger equations[J].Appl Math Comput，2008,203(1):799.

[12] Bao Weizhu,Yang Li.Efficient and accurate numerical methods for the Klein-Gordon-Schrödinger equations[J].J Comput Phys，2007,225(2):1863.

[13] 张鲁明,常谦顺.复Schrödinger 场和实 Klein-Gordon 场相互作用下一类方程组守恒差分格式的收敛性和稳定性[J].高等学校计算数学学报,2000,22(1):362.

[14] Zhang Luming.Convergence of a conservative difference schemes for a class of Klein-Gordon-Schrödinger equations in one space dimension[J].Appl Math Comput，2005,163(1):343.

[15] 王廷春,张鲁明,陈芳启,等.求解 Klein-Gordon-Schrödinger方程组的一个新型守恒差分算法的收敛性分析[J].高等应用数学学报,2008,23(1):41.

[16] 王廷春,郭柏灵.一维非线性Schrödinger 方程的两个无条件收敛的守恒紧致差分格式[J].中国科学:A辑,2011,41(3):207.

[17] Sun Zhizhong,Zhu Qiding.On Tsertsvadze’s difference scheme for the Kuramoto-Tsuzuki equation[J].J Comput Appl Math,1998,98(2):289.