压下量对钢筋矫直系统力学性能的影响分析

，

(沈阳建筑大学交通与机械工程学院，辽宁 沈阳 110168)

压下量对钢筋矫直系统力学性能的影响分析

郑夕健，朱禹霏

(沈阳建筑大学交通与机械工程学院，辽宁 沈阳 110168)

0 引言

钢筋在建筑行业的工程应用非常普遍。钢筋在轧制、冷却、运输过程中由于散热不均、残余应力和外力冲击等因素影响，会出现不同程度的弯曲，所以钢筋在加工使用之前必须对其进行矫直[1]。在矫直钢筋过程中，压下量直接决定矫直质量的好坏，又影响矫直效率，因此，压下量对矫直质量的影响一直是人们重点研究的课题[2]。

钢筋矫直过程中的弯曲变形具有压下量小、弹塑性变形显著和载荷分布多样化等特点，压下量对矫直变形的影响一般除矫直力可以被测量外，变形区的应力、应变大小则很难通过实验或计算得到，造成了认识矫直机理、正确掌握矫直变形规律的困难。

1 矫直系统基本参数的设定

1.1 压下量的设定

随着矫直工作的进行，钢筋将与矫直辊逐个接触，钢筋会受到矫直辊作用，改变钢筋原始弯曲曲率，直至残余曲率符合平直度的要求为止。上排各矫直辊压下量将直接影响矫直过程中与矫直后钢筋内部的应力、应变的变化规律及分布情况，最终影响矫直后钢筋的质量。GT6-12型号矫直机的计算压下量值和实测压下量值如表1所示。其中，l=60时为理论值，l=85时为实测值[3]。

表1 上辊压下量 mm

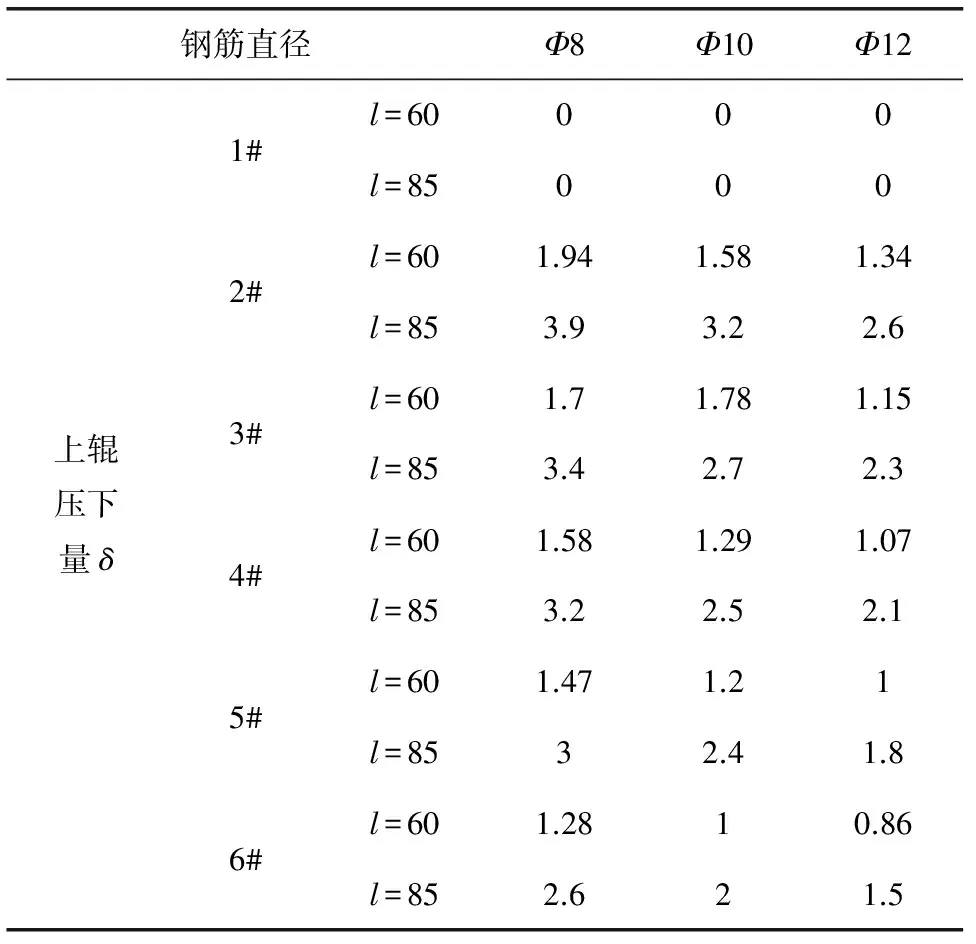
钢筋直径Φ8Φ10Φ12上辊压下量δ1#l=60000l=850002#l=601．941．581．34l=853．93．22．63#l=601．71．781．15l=853．42．72．34#l=601．581．291．07l=853．22．52．15#l=601．471．21l=8532．41．86#l=601．2810．86l=852．621．5

1.2 矫直系统基本参数及钢筋材料属性

矫直辊按照上、下平行交错方式进行配置，在矫直钢筋时，通过上辊下压对钢筋进行重复塑性弯曲以达到矫直目的。选用直径为8 mm、10mm、12mm、长度为1m、牌号为HRB335，即屈服强度为335 MPa的钢筋进行仿真。矫直系统基本参数及钢筋材料属性如表2所示。

表2 基本数据及材料属性

名称参数单位辊径100mm辊数(上6下5)11个辊距60，85mm矫直速度2．88mm/s弹性模量2．03e11Pa钢筋屈服极限3．35e8Pa钢筋直径8～12mm泊松比0．3

2 有限元模型的建立

矫直辊与钢筋均采用8节点solid164单元，该单元是一种8节点实体单元，不需定义实常数，只用在动力显示分析中，支持所有许可的非线性特性[4]。solid164单元有2种算法：一是单点积分法，该方法对大变形问题非常有效，但缺点是有沙漏问题；二是完全积分法，该方法无沙漏问题，但求解慢，若泊松比比较大时要谨慎使用。

因此，选择单点积分法，以便节省时间，只是需要控制沙漏问题[5]。由于矫直辊工作时几乎不变形，所以在有限元建模时把矫直辊设为刚性体，这样可以大大减少显示分析的计算时间，因为无论定义了多少个节点，刚性体都只有6个自由度，刚性体内所有节点的自由度都会自动耦合到刚性体的质心上[6]。钢筋为变形体，选用双向性随动强化材料模型，该模型可以使用2种斜率(弹性和塑性)来表示材料的应力应变行为。

由于矫直辊辊型比较复杂，因此，采用自由网格划分的方式。因为研究对象是钢筋，所以钢筋的网格划分尽量密一些，矫直辊的可以稀疏一些。划分完成后，每个矫直辊单元数为16 000个，Φ8 mm、Φ10mm、Φ12mm钢筋单元数分别为19 456,21952和25 434。

模型中，矫直辊绕中心轴转动，所以除了绕中心轴转动的约束释放外，其余自由度全部约束。由于钢筋矫直时与矫直辊辊槽有接触，接触时矫直力会使钢筋表面有微小变形，使钢筋表面与辊槽面面接触，所以接触类型选择面面接触，选择此类型中的自动接触类型，需定义Contact面和Target面[7]。矫直过程中钢筋会发生弹塑性变形，将其定义为Target面，将矫直辊定义为Contact面，辊子与钢筋之间的静摩擦系数取0.3，动摩擦系数取0.2[8]。

创建原始曲率为零的钢筋进行模拟仿真，计算结束后，在ANSYS后处理器中直接查看钢筋在矫直过程中和矫后的应力、应变特征。

3 有限元仿真分析

3.1 压下量对钢筋应力分布的影响

根据表2设置的矫直参数进行仿真，得到矫直过程中和矫直后的应力等值线图。其中Φ8钢筋的应力等值线如图1,图2所示。

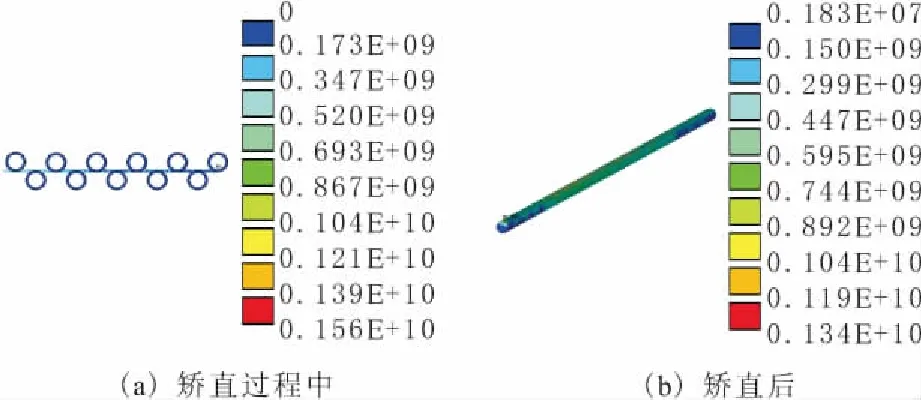
图1 l=60时Φ8钢筋的应力等值线

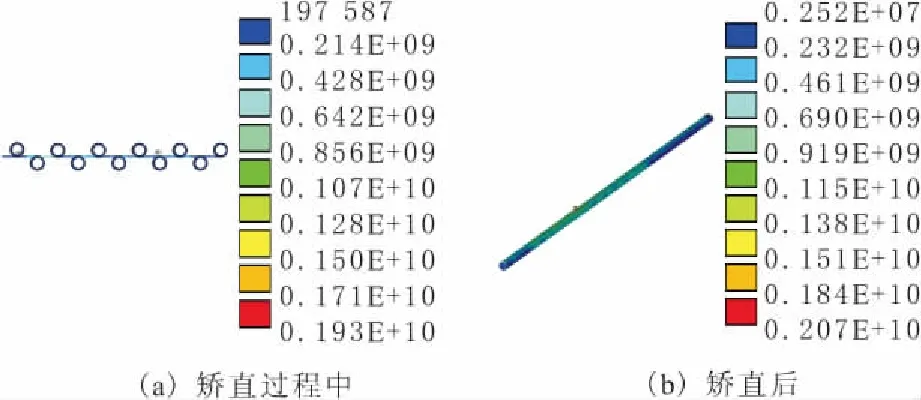
图2 l=85时Φ8钢筋的应力等值线

由图1，图2可以看出，钢筋在l=60的压下量下矫直时，应力主要分布在173～693MPa之间，矫直后应力主要分布在150～595 MPa之间；钢筋在l=85的压下量下矫直时，应力主要分布在214～856 MPa之间，矫直后应力主要分布在232～919 MPa之间。在l=60的压下量下矫直后，钢筋的应力值要小于矫直时的应力值，而在l=85的情况下恰好相反。同时，还发现无论在矫直时还是在矫直后，l=60时的应力值都小于l=85时的应力值，应力分布也比较均匀。

为了研究不同直径钢筋的应力变化情况，列出了Φ10,Φ12钢筋的应力等值线，如图3～图6所示。

图3 l=60时Φ10钢筋的应力等值线

图4 l=85时Φ10钢筋的应力等值线

图5 l=60时Φ12钢筋的应力等值线

图6 l=85时Φ12钢筋的应力等值线

从图3～图6可以明显的看到，粗钢筋矫直后应力值明显低于细钢筋的。同一直径的钢筋在l=60的压下量下矫直时，应力值比l=85时的应力小，且在l=60时矫直后的应力值比矫直过程中的应力值有所减小，这一点对钢筋的仓储、运输及后期的使用有重要意义，可以有效避免钢筋放置后由于内部应力不平衡而再次变形。通过观察矫后等值线图还发现，同一直径钢筋在l=60时，应力值明显低于l=85的应力值，且分布比较均匀，说明理论压下量的矫直方案更加合理。

3.2 压下量与弹塑性应变的关系

为研究压下量与弹塑性应变的关系，以l=60时的压下量，对3种直径钢筋两端面各选取靠近中心的一节点和应力最大处的节点进行弹塑性变化分析。图7,图8为Φ8钢筋应变随时间变化的曲线。

图7 l=60时Φ8钢筋所选节点的弹性应变随时间变化曲线

由图7～图8可以看出，钢筋在矫直过程中，所选端面节点的弹塑性应变很小，可以忽略不计，即中性轴处既不发生弹性应变也不发生塑性应变，说明钢筋矫直时中心轴位置不发生变形，与中性层不变形理论具有一致性，说明应用ANSYS/LS-DYNA软件对钢筋矫直进行模拟是可行的。

图8 l=60时Φ8钢筋所选节点的塑性应变随时间变化曲线

由应变线图还可以看出，塑性应变随时间变化呈现梯形递增趋势，这是因为矫直时，钢筋发生塑性变化后，还会在矫直辊的作用下继续被加载及卸载后又重新加载，屈服极限发生了变化，出现冷作硬化现象，以新的强度进入下一矫直区，进而发生新的塑性变形，直至钢筋走出矫直区。钢筋矫直时最大应变位置靠近表层金属，过大的塑性变形会被释放，所以在l=60时的压下量下矫直时，能够有效防止钢筋表面开裂现象发生。

4 结束语

通过对矫直系统有限元模型的仿真分析，可以得到如下结论：

a.应用ANSYS/LS-DYNA软件对钢筋矫直进行有限元动力学分析，该方法可以直观地对比分析在矫直时和矫直后钢筋内部应力应变的分布情况及变化规律。通过分析发现，矫直时应力主要分布在钢筋表层位置；弹性应变无变化规律，但塑性应变随着钢筋前进而呈现梯形递增趋势，且弹性应变远小于塑性应变；矫直时，钢筋越粗，其应力值越小，说明粗钢筋矫直时所用矫直力越小，更容易被矫直。

b.Φ8钢筋在理论压下量下矫直时，应力主要分布分别在173～693MPa之间，矫直后应力主要分布在150～595 MPa之间；在实测的压下量下矫直时，应力主要分布分别在214～856 MPa之间，矫直后应力主要分布在232～919 MPa之间，在理论压下量下矫直后，钢筋的应力值要小于矫直时的应力值，而实测压下量的情况下恰好相反，观察Φ10、Φ12钢筋的应力等值线图也符合此现象。无论在矫直时还是在矫直后，理论压下量下矫直的钢筋应力值比较小，分布也更加均匀，说明理论压下量下的矫直方案更加合理。

c.在中性轴附近，弹塑性应变在0～4×10-3之间变化，应变值很小，可以认为中性轴应变为零，即中性轴不发生变形；在应力最大结点处，其塑性应变远大于弹性应变，观察不同直径钢筋塑性应变曲线发现，无论钢筋粗细，矫直时最大塑性应变出现在靠近表层位置，过大的塑性变形会被释放，在理论压下量下矫直时，可以有效防止钢筋表面发生开裂现象，能够满足对钢筋表面质量的要求。

[1] 崔 甫.矫直原理与矫直机械[M].北京：冶金工业出版社，2005.

[2] Zhao Binli，Yang Baolai，Zhang Banhua.Reduction of the I-beam straightening the quality of finite element analysis [J].Machinery Design and Manufacture, 2010(6):6-7.

[3] Zheng Xijian,Ma Lei,Zhu Yufei.Analysis of influence of the roller number and rolling schedule to straighten quality of the project steel bar [C]//Applied Mechanics and Materials，2013.

[4] 刘 念.辊式矫直机矫直过程有限元仿真[D].武汉：武汉科技大学，2008.

[5] 杨宝来.型钢矫直机理的数值模拟及实验研究[D]. 秦皇岛:燕山大学，2010.

[6] 孟欣佳,张立香. 钢筋弯曲过程的有限元模拟[J].河北工程大学学报(自然科学版)，2011，28(2)：30-32,37.

[7] 周存龙,王国栋,刘相华,等.压弯量对轧件矫直变形影响的有限元分析[J]．塑性工程学报，2006(1)：78-81.

[8] 尚晓江,苏建宁.ANSYS/LS-DYNA动力分析方法与工程实例[M]．北京：中国水利水电出版社，2006.

Analysis of the Influence of Rolling Schedule on Mechanical Characteristicsof Straightening System of Steel Bars

ZHENGXijian,ZHUYufei

(School of Transportation and Mechanical Engineering, Shenyang Jianzhu University, Shenyang 110168，China)

以十一辊平行辊矫直机为原型，运用有限元分析软件ANSYS/LS-DYNA建立了钢筋矫直系统有限元模型；在理论压下量和实测压下量下，分别对3种不同直径的钢筋进行了动力学仿真分析，得到了钢筋在矫直过程中与矫直后的应力大小及分布情况；分析并比较了在理论压下量和实测压下量下，端面中心节点处与应力最大点处的弹塑性应变变化规律，找到了相对合理的压下量方案。该研究结果对掌握钢筋矫直过程的力学特性变化和提高矫直质量具有一定的参考价值和实际意义。

钢筋矫直；压下量；应力；应变

Taking eleven-roll parallel roll straightening machine as a prototype, the authorsestablished a FEM of straightening system of steel bars by ANSYS/LS-DYNA； under theoretical and measured rolling reduction, the authors simulated the process for straightening steel bars of three different kinds of diameter and did kinetic analysis, as a result, the authors obtained stress and its distribution in the process of straightening and after straightening； through analyzing and comparing the change rules of elastic and plastic strain at the center node of each face and at the biggest stress point under theoretical and measured rolling reduction, the authors found a comparatively reasonable rolling schedule. The study provides certain references for mastering mechanical characteristics of straightening process and improving the quality of straightening and it has practical significance.

straightening steel bars； rolling reduction； stress； strain

2014-05-07

“十二五”国家科技支撑计划资助项目(2011BAJ02B03-3)

TH12

A

1001-2257(2014)09-0015-04

郑夕健(1963-)，男，山东容城人，教授，研究方向为建筑机械设计理论、钢结构稳定理论、建筑结构动力学分析、有限元结构分析和建筑机械产品开发等；朱禹霏(1990-)，女，辽宁沈阳人，硕士研究生，研究方向为工程机械现代设计方法。