基于滚轮导轨接触模型的高速重载运动机构振动与疲劳分析

，，

(哈尔滨工业大学机器人技术与系统国家重点实验室，黑龙江 哈尔滨 150001)

基于滚轮导轨接触模型的高速重载运动机构振动与疲劳分析

王锐，刘延杰，杨立冬

(哈尔滨工业大学机器人技术与系统国家重点实验室，黑龙江 哈尔滨 150001)

通过赫兹接触理论对滚轮导轨系统建立接触力学模型，推导接触刚度、强度的计算公式，并分析滚轮、轴承的总接触刚度。根据接触刚度模型、应用拉格朗日方程建立高速重载运动机构动力学模型，得到机构的自由振动微分方程，从而计算出机构的各阶固有频率。

滚轮导轨；接触力学；拉格朗日方程

0 引言

高速重载运动机构是Z箍缩驱动的混合堆快速换靶机构的重要环节，其作用是当运输小车运动到靶室正上方时，带动RTL组件，将其送入靶室。机构做竖直方向的一维运动，行程达15 m，机构与负载总重约为25 t，由于换靶频率要保证0.1Hz，机构运动速度也非常高，最高速度将达到15 m/s。在高速重载工况下，滑动导轨摩擦力大，发热大故无法适应连续、精度要求高的工作条件。而在滚动导轨中，以滚轮导轨的承载能力最为出众，因此，选择许用速度达15 m/s的滚轮导轨作为导向结构。针对滚轮导轨这一导向部件，需要满足高速重载运动机构的强度与动态性能要求，作出以下分析。

1 建立接触模型

由于导轨和滚轮的相互接触是诱发系统振动和导轨疲劳破坏的根源，因此，建立简单有效的导轨一滚轮接触模型是分析系统振动的基础。假定导轨与滚轮间只考虑法向力，采用经典的赫兹弹性接触理论进行计算。

当圆柱体受到单位长度上的压力为p时，圆柱体间就会发生接触变形。在接触长度为L，宽度为 2a的接触区[1-3]，根据Hertz接触理论可得：

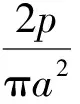
(1)

最大压力为：

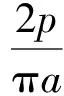
(2)

对于圆柱体与平面接触，可以看作是曲率半径为R和曲率半径为无穷大的2个轴线平行圆柱之间的接触。

当圆柱为有限长时，圆柱与平面的趋近量不适合用Hertz理论求解。工程应用时，由于受力情况复杂，主要采用Palmgren通过实验得出的经验公式[4]，对于钢材料的接触，弹性模量E=206 GPa，泊松比u=0.3，即

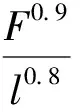
(3)

F为法向力；l为接触长度。因此，可以得到法向力与趋近量的关系为：

F=a·δ10/9

(4)

a为与l有关的参数。可见，法向力与趋近量之间呈现非线性关系，然而非线性程度并不高，在趋近量小的时候是可以用线性关系近似的。

对于滚轮导轨副，当导轨、滚轮位移都比较小，滚轮上作用有预加力，滚轮产生的预加变形为δ0时，并且预加位移相比导轨、滚轮的位移较大，式(4)可以用泰勒级数展开，得到：

(5)

用f0表示上式中第1项，并以Kg表示第2项系数，则式(5)中接触力计算公式可以写为：

f=f0+Kgdδ

(6)

f0为预加力；Kg为近似线性化接触刚度，dδ为滚轮和导轨间的相对位移。公式转化为线性化的接触力表达式。预紧量为0.1mm时，预紧力f0=1.73×104N，径向刚度Kg=1.92×105N/mm。

滚轮为V型结构，夹角为90°。当径向力F作用于滚轮时，滚轮与导轨之间产生的径向位移为dx，那么对于接触面上产生的趋近量则为：

dδ=dxsinφ

(7)

由此可得，滚轮与导轨间单个接触表面间增加的法向接触力和接触力在dx方向上的分量为：

fx=Kgdδsinφ=Kgdxsin2φ

(8)

由力平衡关系可得：

F=2fx=Kgdx

(9)

同理可以得到，滚轮导轨的径向刚度和轴向刚度均为Kg。滚轮接触模型如图1所示。

滚轮与导轨的接触可以认为是线接触，而对于滚轮轴承来说，其中的钢珠与轴承框架则为点接触，根据Hertz接触理论，当2个接触的外凸形状的固体相互挤压时，接触点扩展为1个区域，在接触区域内会产生应力和变形。接触斑的大小取决于接触体的力学属性和外部载荷。

图1 滚轮接触模型

对于弹性圆球点接触，接触半径和接触应力分布可由下式给出[1，5-7]，即

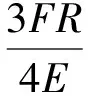
(10)

最大压力为：

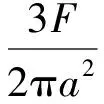
(11)

由于接触部位附近的变形，接触体将会相互趋近。Hertz接触载荷与趋近量的关系为：

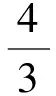
(12)

工程实际应用中常保持预紧量为60μm，当变形量较小时，F-δ关系近似为线性关系，钢珠直径为12mm，复合弹性模E=1.03×1011Pa，线性拟合后近似线性刚度为KB=1.51×105N/mm，经线性拟合的F-δ关系和原曲线如图2所示。从图2可以看出，线性拟合刚度和实际刚度的差别很小，最大误差为3.65%。

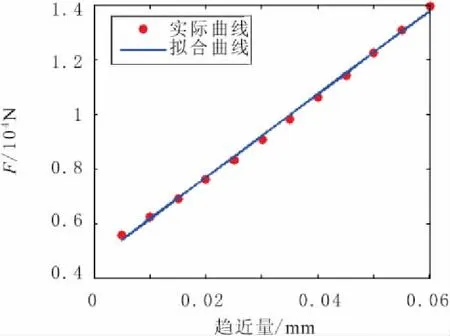
图2 滚珠刚度线性拟合曲线

如此滚珠接触等效为弹簧，当滚珠两端同时有接触力作用时，就是一对弹簧的串联问题。若每根弹簧的刚度为KB，则每个接触面的刚度为KB/2。轴承内圈固定，当外圈受轴向力F时，竖直下降位移为δ。接触点由A点移动到A1点，D点移动到D1点。轴承接触模型如图3所示。

图3 轴承接触模型

从图3可知，AC接触对之间的接触变形改变量δAC=AA1。因此，接触变形量为：

δAC=δsinα，δBD=-δsinα

(13)

对轴承外圈进行受力分析得：

F/Z=FACsinα-FBDsinα=Kbδ

(14)

Z为钢珠数量，轴承共两排钢珠，每排12个，共24个，所以轴承的轴向刚度为Kba=24Kb=18.12×105N/mm。

当轴承受到径向力F作用时，受力情况如图4所示。因预紧作用，各钢珠均受力，而受力情况各不相同，越靠近受力点的钢珠接触力越大。各钢柱法向接触力为Fj。由受力分析得：

(15)

当产生位移量δ时，每个滚珠的接触变形变量为δj，δj=δcosαcosβj，法向接触力FAC=FBD=Kb(δ0+δjcosα)，因此，有：

Fj=FAC+FBD=2KB(δ0+δcos2αcosβj)

(16)

由此可得：

(17)

所以轴承径向刚度Kbr=9.06×105N/mm。

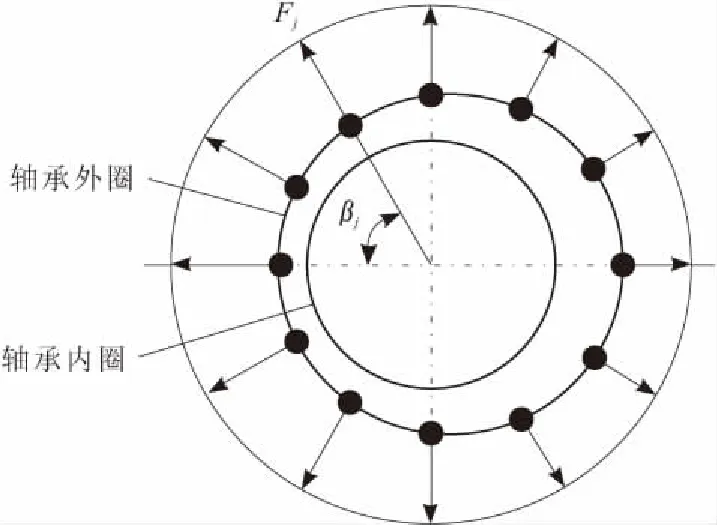
图4 轴承径向受力分布

2 振动特性分析

机构做竖直方向的一维运动，两边各有2组导轨，每组导轨有4对滚轮。据上述计算结果简化模型[8-10]，将接触作用等效为弹簧单元，滚轮所在位置的滚轮-导轨接触和轴承接触可以等效为2个弹簧单元串联之后的结果。坐标系建立方式如图5所示。设x轴方向弹簧刚度为kx，y方向弹簧刚度为ky。

(18)

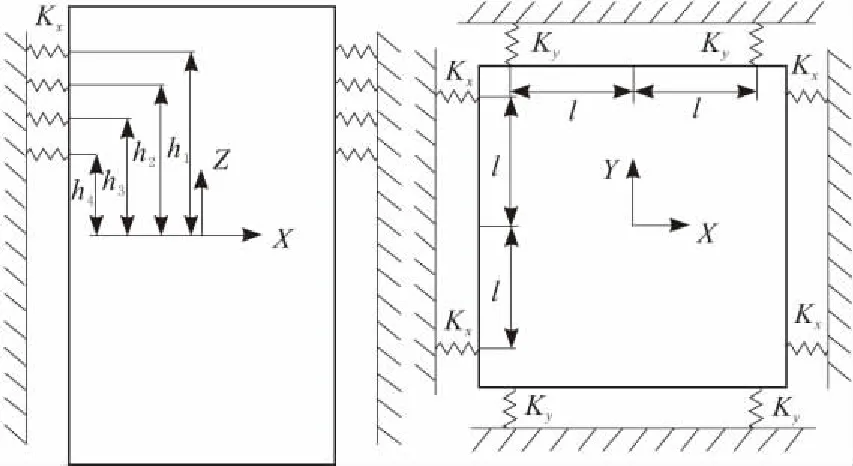
图5 动力学模型

采用拉格朗日法建立动力学方程[10-11]，设系统绕x轴，y轴，z轴的坐标分别为φ，θ，Φ，则系统沿x轴，y轴和绕x轴，y轴，z轴的振动方程可表示为：

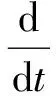
(19)

qi为系统的广义坐标；T为系统动能；V为系统势能。系统动能为：

(20)

m为机构运动部分总质量；Jx，Jy，Jz分别为机构绕x轴，y轴，z轴的转动惯量。由系统的动能可以得到惯性力方程为：

(21)

系统的势能为：

(22)

Kx为x方向弹簧刚度；Ky为y方向弹簧刚度；Δxi，Δyi分别为x方向，y方向第i个弹簧的伸长量。由系统势能可以得到弹性力方程为：

(23)

根据惯性力方程、弹性力方程得到系统的无阻尼振动方程，方程改成矩阵形式为：

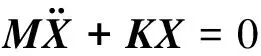
(24)

X为系统的坐标位移矩阵，即

X=[x，y，φ，θ，φ]T

(25)

M为系统质量矩阵；K为刚度矩阵。

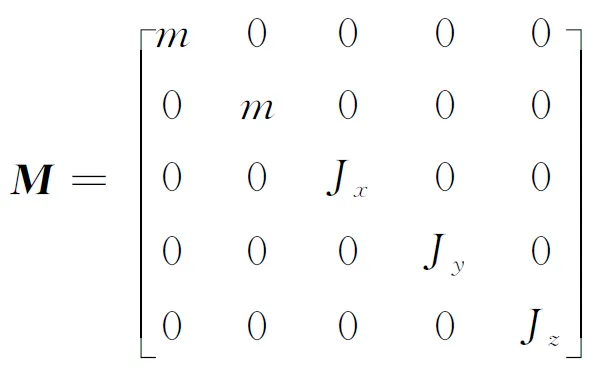
(26)

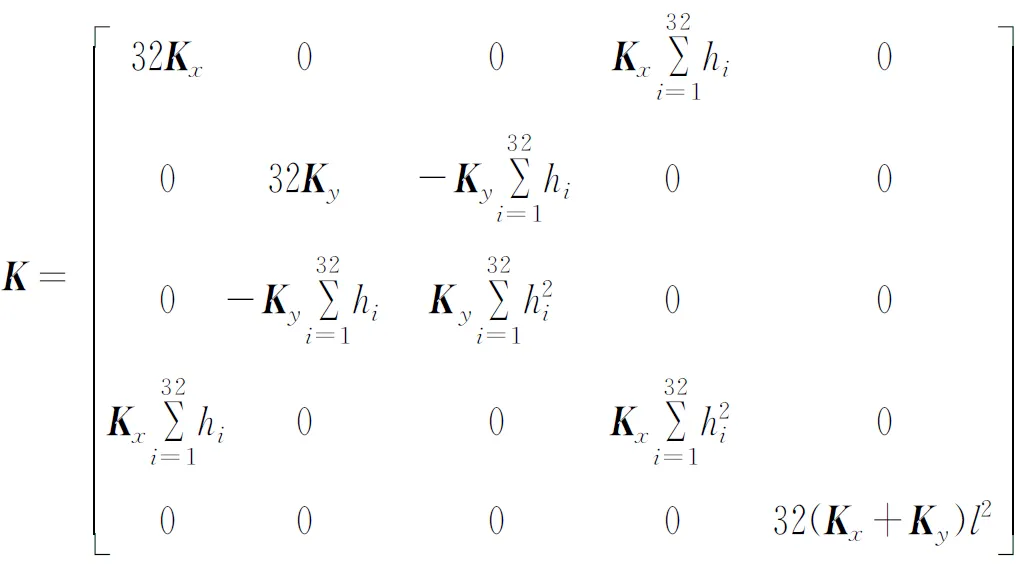
(27)

求解系统特征方程可得系统固有频率。对比ANSYS仿真结果发现，计算误差相差无几。系统基频超过了10Hz，满足工作需要。结果如表1所示。

表1 固有频率计算结果 Hz

3 疲劳特性分析

因高速重载运动机构的尺寸很大，难免产生偏心距。设质心偏离几何中心线距离为ε，取向右方向为正方向，力矩顺时针为正。根据运动轨迹，计算倾覆力矩。下降阶段重力产生的倾覆力矩始终为(m1+m2)gε，上升过程为m1gε，其中，m1为滑块等组件质量，m2为RTL组件质量。过程中惯性力产生的倾覆力矩为(m1+m2)aε，上升过程电机作用力产生的倾覆力矩为(m1)aε。根据运动轨迹可计算出倾覆力矩循环，如图6所示。

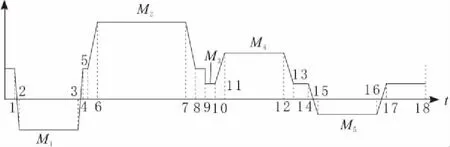
图6 倾覆力矩循环

机构倾覆力矩将由导轨支持力平衡，这样将对滚轮导轨产生压力，根据平衡条件可计算滚轮所受压力，最外侧的一组滚轮受力最大为：

(28)

Li为第i组滚轮距离滚轮组对称轴的距离，i=1，2，3，4。由Hertz理论可知，滚轮中轮径小处的接触力大于轮径大处的接触力，所以只需计算轮径最小处在工作过程中的应力-时间数据。

滚轮采用GCr15材料，疲劳极限250MPa，屈服极限518 MPa，构件承受的应力幅水平与发生疲劳破断时所经历的应力循环次数之间的关系，多用如幂函数的形式表示[12-13]，即

(29)

S为应力幅；m，C为与材料有关的常数。循环次数N=1时，S为屈服强度Sq，对于金属材料，疲劳极限Sh所对应的寿命一般为N=107次，这样已知Sq和Sh的情况下，就可以联立求解出常数m=22.12和C=1.13×1060，从而近似得到材料的S-N曲线，如图7所示。

由Hertz接触理论可以计算滚轮所受的接触力-时间数据，对应力谱的处理采用雨流计数法，这样就可以得到各级应力的均值与幅值。

图7 导轨材料S-N曲线

由于应力均值对疲劳累积损伤的影响，必须对雨流计数的结果进行应力均值修正，将非零应力均值的应力范围转化为零应力均值的应力范围[14-17]。利用Sederberg直线将变幅疲劳应力修正为平均应力为零(即应力比为-1)的疲劳应力谱，即对称循环载荷谱。

Sederberg直线的表达式为：

Si=Sai/(1-Sni/SJ)

(30)

Si为第i级应力循环的等效应力；Sai为第i级应力循环的应力幅值；Sni为第i级应力循环的应力均值；SJ为材料的屈服强度。将雨流计数法得到的Sai和Sai代入即可求得对称循环应力。

图8为用雨流计数法计算得到的等效应力，经计算各级应力均远小于疲劳极限，其中最大级应力为S=94.19 MPa。也即各级应力对疲劳寿命没有影响，可认为滚轮工作循环数为107。

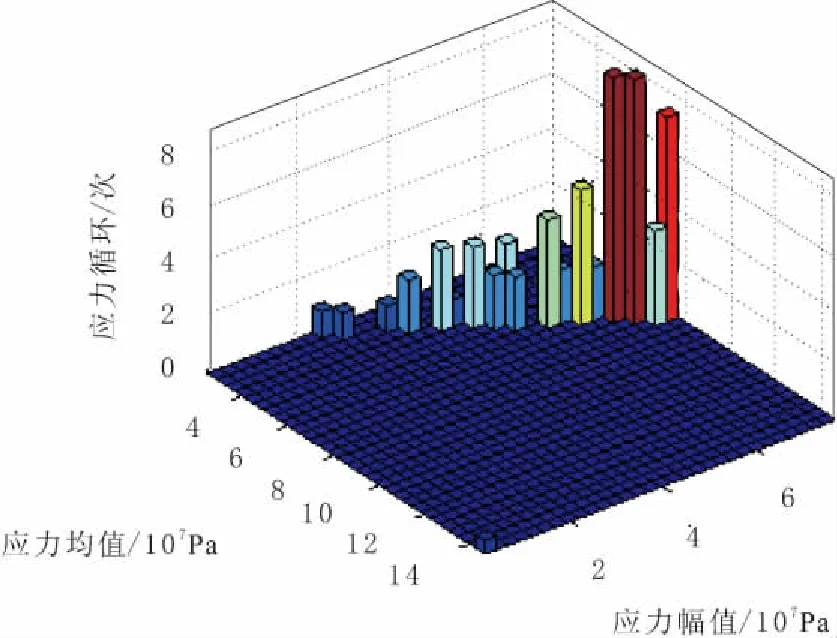
图8 接触力分布

4 结束语

基于赫兹接触理论对滚轮导轨系统建立了接触力学模型，得到滚轮、轴承的总接触刚度。根据接触刚度模型、拉格朗日方程法建立了高速重载运动机构动力学模型，得到机构的自由振动微分方程，从而计算出机构的各阶固有频率，其一阶固有频率为13.4Hz。借助有限元分析软件ANSYS对机构进行模态分析，与理论计算结果进行对比，验证了方法的正确性。对滚轮导轨进行了接触疲劳强度分析。采用雨流计数法和Sederberg直线处理接触应力载荷谱，计算出滚轮导轨的最大级循环应力为95 MPa。

[1] Johnson K L. 接触力学[Z].剑桥大学出版社，1985.

[2] 刘曙光. 滚柱直线导轨副的力学性能分析[D]. 武汉：华中科技大学，2011.

[3] Chen J L，Wijaya M T. The control of long-range single-axis nanometer positioning system[C]//International Design Engineering TechnicalConferences & Computers and Information in Engineering Conference,New York，2008.

[4] Wu J S，Chang J，Hung J. The effect of contact interface on dynamic characteristics of composite structures[J]. Mathematics and Computers in Simulation,2007,74(6):454-467.

[5] Ohta H，Kitajima Y，Kato S，et al. Effects of ball groupings on ball passage vibrations of alinear guideway type ball bearing(pitching and yawing ballpassage vibrations)[J]. Journal of Tribology，2007，129(1): 188-193.

[6] Zhang Xueliang．Mechanical joint surface dynamic characteristics and application[M]．Beijing：China Science and Technology Publishing House，2002．

[7] Fujiwara H. Logarithmic profiles of rollers in roller bearings and optimization of the profiles[Z]. Kawase T，2007.

[8] 李丹达. 电梯轮轨耦合振动建模及分析[D].上海： 同济大学，2006.

[9] Sun W，Wang B，Wen B C. Dynamics characteristics testing and parameter identification for joints of linear rolling guide way[J]. Journal of Northeastern University，2011，32(5): 716-719.

[10] Liu Yanjie，Song Lei，Liu Niuniu. Modeling and parameter identification of the cross roller guide way[C]//Proceedings of the IEEE/ICMA International Conference on Mechatronics and Automation，2012:692-696.

[11] Zhou Chuanrong. Structural dynamic design[J]. Journal of Vibration Measurement and Diagnosis，2001，21(1):1-7.

[12] Xie Jilong. Dynamic response and fatigue strength of depressed center flat frame[J]. Journal of Mechanical Engneering，2010,46(16):16-22.

[13] Howell L J．Power spectral density analysis of vehicle vibration using the NASTRAN computer program[J]．SAE Tramns,1974,83(2)：1415-1424．

[14] Pen Zunsong.Vehicle system dynamics[M]．Beijing：China Railway Publishing House，2007．

[15] 谢基龙，张 燕，谢云叶. 铁路凹底平车凹底架动态响应及其疲劳强度[J].机械工程学报，2010，46 (16):16-22.

[16] British Standards Institution．BS EN 1993·l·9 2005 Euroeode 3.Design of steel structures．Fatigue[S]．London：British Standards Institution，2005．

[17] 辛天佐. 轻量化 LNG 罐车的强度分析与疲劳研究[D].南京：南京理工大学，2012.

Vibration and Fatigue Analysis of High-speed Heavy Mechanism Basedon Roller Contact Model

WANGRui，LIUYanjie，YANGLidong

(State Key Laboratory of Robotics and System，Harbin Institude of Technology，Harbin 150001，China)

Established the mechanism’s roller guide contact mechanics model by Hertz contact theory，derived contact stiffness，strength calculation and analyze the total contact stiffness of the wheels and the bearing. According to the contact stiffness model of high-speed heavy motion mechanism，established dynamic mode by using Lagrange equations of motion mechanism，Thus，established freedom vibration differential equation to calculate the natural frequencies of mechanism.

roller guide；contact mechanics；Lagrange equation

2014-05-05

黑龙江省科研机构创新能力提升专项计划项目(YC13D004);国家高技术研究发展计划(八六三)资助项目(2013AA040901)

TH112

A

1001-2257(2014)09-0047-05

王锐(1989-)，男，黑龙江佳木斯人，硕士研究生，研究方向为机械电子工程；刘延杰(1975-)，男，黑龙江哈尔滨人，教授，研究方向为机器人技术。