动力稳定车旁承动态特性研究

, ,

(1.河南省机械设计研究院有限公司，河南 郑州 450002; 2.郑州宇通重工有限公司，河南 郑州 451482)

动力稳定车旁承动态特性研究

李胜军1,刘光伟2,李晓鹏1

(1.河南省机械设计研究院有限公司，河南 郑州 450002; 2.郑州宇通重工有限公司，河南 郑州 451482)

在研究动力稳定车整体性能中，旁承动态特性是其关键因素之一。在确定了旁承橡胶弹簧的本构参数下，建立了旁承的有限元模型，并基于动态特性分析研究了其垂向的动态特性。研究结果表明，不同载荷和频率组合下，旁承橡胶弹簧常数及内部阻尼动态特性呈现非线性变化，为旁承优化设计提供了理论依据。

旁承；有限元分析; 动态特性

0 引言

橡胶材料在国民经济生活中占有重要地位，具有广泛用途[1]。橡胶材料显著的高弹性和非线性运用到车辆设计中，可以很好地满足车辆的需要[2]。国内外对此进行了研究[3-5]。但在铁路车辆应用橡胶弹簧研究其非线性特性还不够深入。因此，以旁承弹簧为研究对象，通过实验确定其本构参数，运用非线性分析研究其动态特性，为后续优化提供依据。

1 旁承弹簧本构参数的确定

在橡胶材料的模型中，Moony-Rivlin模型以及Ogden Model使用较为广泛[6]。因此，以Moony-Rivlin模型建立旁承弹簧的模型。通过计算公式可得其变形能量密度参数[7]，即

(1)

(2)

2 有限元模型的建立

旁承橡胶弹簧在弹簧座内工作，其上装有止推盘和尼龙摩擦板。当弹簧顶盖受压向下运动时，可看作是一较柔的刚度特性；当向下压缩到一定程度时，弹簧胶体和弹簧座内壁开始接触，可看作一较硬的刚度特性。旁承结构如图1所示。

图1 旁承结构

鉴于旁承橡胶弹簧的受力对称性。选取1/2进行简化，简化后旁承模型如图2所示。其参数为：

ρ=1155 kg/m3；泊松比μ=0.499；C10=1MPa；C01=1.65 MPa。其余ρ=7 850kg/m3；E=2.1×e11Pa ，泊松比μ=0.3。

有限元网格如图3所示。弹簧底面完全约束，并在接触的地方建立接触对。

图2 简化后旁承模型

图3 旁承有限元网格

3 旁承动态特性研究

3.1 旁承动态特性研究方法

橡胶减震器研究与传动振动隔离运动不同，其阻尼力与振动速度不完全成正比，而具有滞后性质。所以，采用复刚度K*表示[8]，即

K*=K′+jK″=K′(1+jη)

(3)

K*为复刚度；K′为存储弹簧常数；K〃为损耗弹簧常数；η为损耗系数；η=K〃/K′。复刚度的模又称为绝对弹簧常数，其值为：

(4)

采用非谐振法研究其动态特性得其系统模型如图4所示[9]。其运动方程为：

(5)

图4 系统物理模型

F(t)分解为X同相的Fa和异相Fb1，则：

(K′-Mω2)X+jK″X=Fa+jFb

(6)

由式(6)可得：

(7)

当力F和位移X间的相位角为φ时，有

(8)

将式(8)代入式(7)得：

(9)

F为正弦激励动力幅；X为位移响应幅值；φ为同一时间内载荷超前位移的相位角。从载荷超前位移响应的时间差Δt求得φ=360°Δt/T，T为激励力周期；ω为激励频率；M=5.76 kg为系统当量质量。

3.2 旁承动态特性分析

用动态非线性分析方法来研究旁承动态特性。在模型中加入正弦激励。分2种工况研究：

a.频率为定值40Hz，动力幅值不断变化，变化范围为1000～10000N，增量为1000N。

b.动力幅为定值10000N，频率不断变化，变化范围为40～80Hz，增量为5 Hz。

由图5，图6可以看出，在频率不变，动力幅值变化的情况下，存储弹簧常数K′呈现增长趋势，损耗弹簧常数K″、相位角φ呈现下降趋势，而绝对弹簧常数|K*|呈现增长趋势。当动力幅值不变时，频率变化时，由图7、图8可以看出，存储弹簧常数K′、损耗弹簧常数K″、相位角φ以及绝对弹簧常数|K*|都呈现增长趋势，并都具有明显的非线性特性。

图5 相同频率作用下K′和K″ 随动力幅变化曲线

图6 相同频率作用下φ和|K*|随动力幅变化曲线

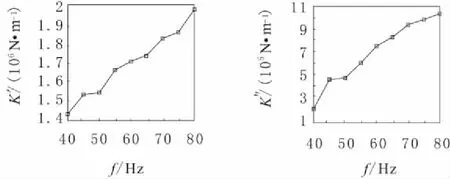
图7 相同动力幅作用下K′和K″ 随频率变化曲线

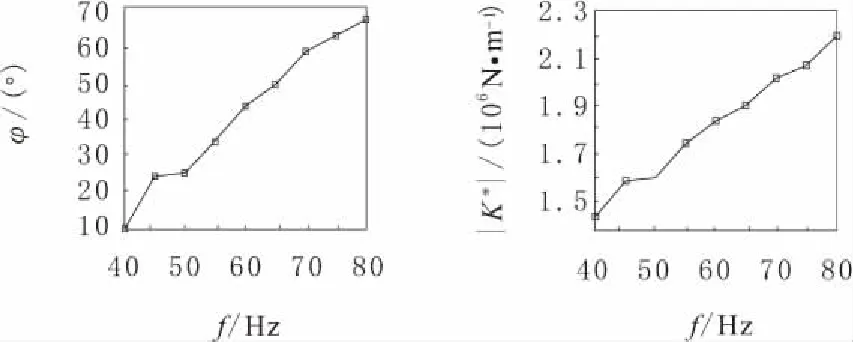
图8 相同动力幅作用下φ和|K*|随频率变化曲线

4 结束语

分析结果可以得出，2类工况下，绝对弹簧常数|K*|的变化具有相似的过程，它表明旁承内部阻尼特性随频率和动力幅值而变化的本质关系；一方面是存储弹簧常数K′、损耗弹簧常数K″的变化；另一方面是相位角φ的变化，不同的载荷、频率组合下，发生变化的值不同。

[1] 秦怀德,武冠英.合成橡胶[M],北京:化学工业出版社,1988.

[2] 牟传文,詹雯生.防振橡胶及其应用[M].北京:中国铁道出版社,1982.

[3] Berg M.A non linear rubber spring model for rail vehicle dynamic analysis[J]. Vehicle System Dynamics,1998, 30(3):197-212.

[4] Sjoberg M, Karl L. Non-linear behavior of a rubber isolator system using fractiona1derivatives[J]. Vehicle System Dynamics,2002,7(3):217-236 .

[5] 姜洪源,郝德刚,敖宏瑞.环形金属橡胶隔振器系统建模与实验研究[J]. 湖南科技大学学报, 2005, 20(1):13-16.

[6] 何 涛,杨 竞.ANSYS10.0/LS-DYNA非线性有限元分析实例指导教程[M].北京:机械工业出版社,2007.

[7] 李方泽,刘馥清,王 正.工程振动测试与分析[M].北京:高等教育出版社,1992.

Research on the Dynamic Characteristics of the Dynamic Track Stabilizer Side Searing

LIShengjun1,LIUGuangwei2,LIXiaopeng1

(1.Henan Machinery Design and Research Institute Co., Ltd., Zhengzhou 450002，China; 2.Zhengzhou Yutong Group Co., Ltd.,Zhengzhou 451482,China)

In the overall performance of the dynamic stability of the car,the side bearing dynamic characteristics is one of the key factors. This paper determined the constitutive parameters of side bearing rubber spring and establish the finite element model, the side bearing,dynamic characteristic and dynamic characteristic analysis was based on the vertical.According to the results, different load and frequency combinations of side bearing rubber spring constants and internal damping characteristic of nonlinear change.The conclusion can provide a theoretical basis to the optimal design of side searing.

side bearing; finite element analysis；dynamic characteristic

2014-04-17

TH113

A

1001-2257(2014)09-0042-03

李胜军(1984-) ，男，河南开封人，工学硕士，研究方向为机械设计与制造。