基于混沌不变量和关联向量机的人体行为识别*

戴志强，董坚峰

(吉首大学旅游与管理工程学院，湖南 张家界 427000)

基于混沌不变量和关联向量机的人体行为识别*

戴志强，董坚峰

(吉首大学旅游与管理工程学院，湖南 张家界 427000)

提出了一种基于混沌不变量特征和关联向量机(RVM)的人体行为识别方法.提取人体关节点运动产生的轨迹代表人体动作行为的非线性系统，利用 C￣C方法估计时延并且得到由每条运动轨迹重构的相空间维数，并从重构的相空间提取代表人体行为的混沌不变量，利用RVM算法识别人体行为.在KTH，Weizmann及ballet 数据库中进行测试，实验结果表明，使用该方法平均正确率达92.1%.

混沌系统；行为识别；混沌不变量；RVM

人体行为识别是计算机视觉领域一个重要的方面，它应用于诸如视频监督、娱乐、用户接口、运动、视频理解以及病人监护系统等领域.当前，基于静态图片或者视频序列的人体行为识别已经取得了很多研究成果：基于动作片段的行为识别方法[1-2]，基于时序动态模型[3-4]的行为识别方法，以及基于关键点[5-7]的行为识别方法等等.文献[8]中提出了一种利用混沌系统的理论来识别人体行为的框架，它通过交互信息和假最近邻算法对每一条时间序列在相空间中进行嵌入，从而获得每条时间序列的混沌结构.但是，交互信息的方法计算十分繁琐且需要大的数据集，并且时延和嵌入维数彼此是不相关联的，另外最大李雅普诺夫指数是由定义计算出来的，其结果对于小数据集来说不太可靠，而且相对较难以实现.

为了克服上述方法的缺点，笔者提出了一种使用混沌系统理论的新的行为识别方法.提取人体关节点运动的轨迹来表示一个确定的人体行为的非线性动态系统，而这个非线性动态系统可以通过混沌的理论进行分析.利用C￣C方法来估算重构的相空间的时延和嵌入维数，同时，使用一个实用的方法从小数据集中计算出最大李雅普诺夫指数.最后，使用RVM识别人体行为.新方法容易实现，而且对小数据集很有用，计算比较简单.

1 人体动作的相空间重构

1.1人体动作的表示

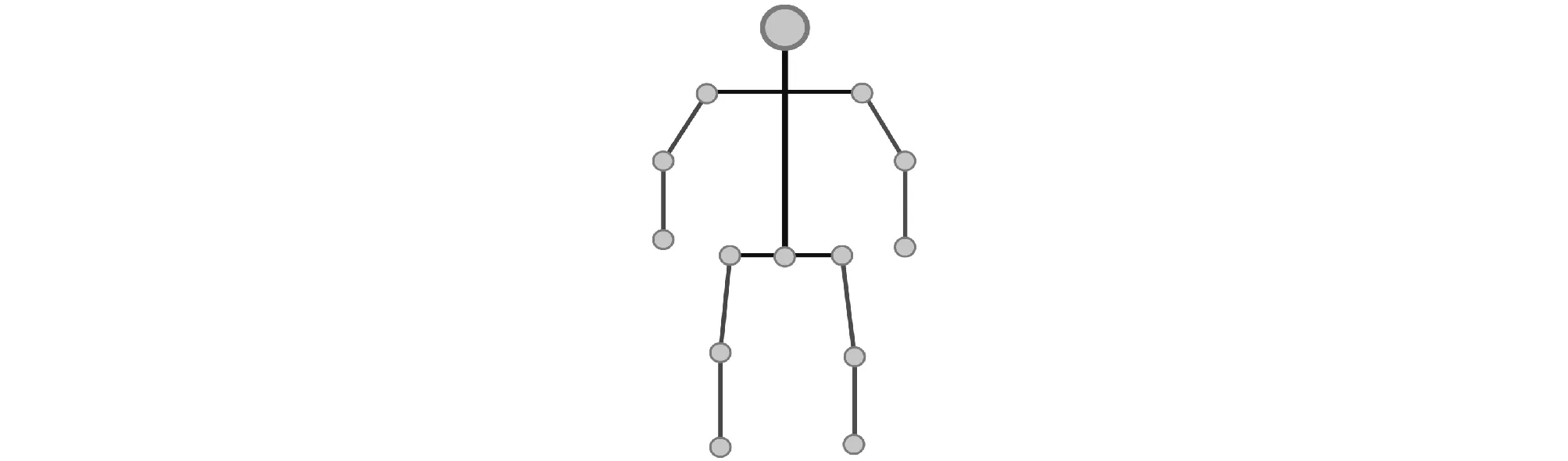
图1 人体3D模型

人的身体可以用12个刚性部分来建模：臀部、肢体、肩膀、脖子、2条大腿、2条小腿和2只手臂以及2只前臂[9].这些部分由是个内部结点连接起来，如图1所示.

图2 左手臂结点的定位

为了得到人体关键点运动的轨迹，选择10个具有代表性的关键点，例如头、2只手臂、2只手、2条大腿、2只脚以及肚子部分，这些点可以为大部分的行为动作提供足够的信息.而这些被选的关键点可以通过在3D空间[10]定位所获得，每个结点随着时间的推移通过3D轨迹估计[11]的方法追溯每个结点的运动轨迹.身体关键点的运动轨迹组成了一个确定的、非线性的人体行为动态系统.图2表示在3D空间中所定位的人的手臂结点.图3表示从图2所示左手臂结点运动中提取的时间序列.

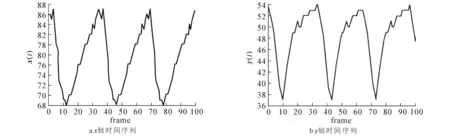
图3 由图2中左手臂结点运动中提取的时间序列

通常情况下，动态系统可以由状态空间模型表示，其状态空间变量X(t)=(x1(t),x2(t),…,xn(t))∈Rn表示在确定的时间t系统的状态，状态变量空间通常被称为相空间.系统状态根据一个确定的演变函数以及随着时间的推移系统状态变化生成的轨迹发生变化.图4表示由人体10个关键点运动所产生的运功轨迹.人体行为的相空间可以用这些运动轨迹重构，从而可以获得一些表示人体动作行为的混沌不变量.

图4 由一些动作所产生的轨迹例子集

1.2人体动作行为的相空间重构

为了从时间序列中提取更多有用的信息，Packard N H等[12]提出用时间序列重构相空间的2种方法，即导数重构法和坐标延迟重构法.

使用文献[8]中介绍的利用互信息重构相空间过程中，选择吸引子时延τ有很多缺点，如不一致性、计算时间较长且需要大数据等问题.所以，对于时延窗口τw=(d-1)τ，使用C￣C方法[13]笔者选择时延以确保xi分量的独立，并得到嵌入的维数d.

为研究非线性依赖性以及消除虚假的时间相关性，时间序列{x(i)}(i=1,2,…,N)被分成t个不相交的时间序列，每个时间序列的长度NS=N/t，其中t表示相空间重构的时延，x1={x1,xt+1，…，xN-t+1},x2={x2,xt+2,…，xN-t+2},…,xt={xt,x2t，…，xN}.

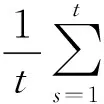
其中：S(d,N,r,t)=C(d,N,r)-Cd(1,N,r)；C(d,N,r)表示相关积分；N表示数据集的大小；d表示嵌入的维数.当N→∞,

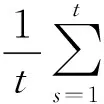
选择rj的几个代表值，定义ΔS(d,t)，

ΔS(d,t)=max{S(d,rj,t)}-min{S(d,rj,t)}.

(1)

(1)式衡量了S(d,r,t)随着r的变化而产生的变化量.局部最优时间t是S(d,r,t)的过零点和ΔS(d,t)的最小值的时间.S(d,r,t)过零点对所有的维数d和r应该大致相同，而ΔS(d,t)的最小值对所有维数d也应该大致相同.时延τd对应于第1个得到的局部最优时间.

通过上述方法得到维数d和时延τd以后就可以重构人体行为动作的相空间了.C￣C方法很容易实现，更适用于小数据集，计算量较小.维数d的估计值与第1个互信息的局部最小值一致.

2 人体行为的不变量特征

人体行为可以通过下文介绍的相空间重构方法重构相空间从而得到相空间不变量.其中，相空间不变量特征包括相关积分、最大李雅普诺夫指数和kolmogorov￣sinai熵.

2.1相关积分

嵌入时间序列相关积分[14]定义如下：

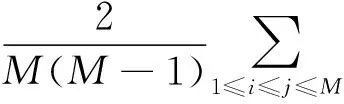
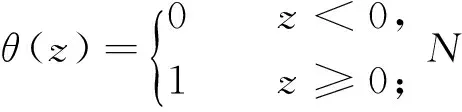
2.2最大李雅普诺夫指数

李雅普诺夫指数是用以度量相空间中2条相邻轨迹随时间按指数律分离的程度，是一个统计平均量[15].因为用文献[8]中方法计算最大李雅普诺夫指数对于小数据集不太可靠，而使用文献[16]中一个有效的方法可以从小数据集中计算出最大李雅普诺夫指数，这种方法快速，容易实现并且同时对于大数据集同样适用.其算法步骤如下：

(1)计算时延τ，嵌入维数d和平均周期p.

(2)重建相空间Xi= (xi,xi+τ,…,xi+(d-1)τ)∈Rd(i=1,2,…,M).

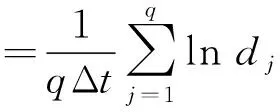
(5)通过对平均直线y(i)的最小二乘法可以简单且准确地计算出最大李雅普诺夫指数λ1.

2.3Kolmogorov￣Sinai熵

与文献[8]中的关联维数相比，Kolmogorov￣Sinai熵是动态系统的一个重要特点，发映了更多混沌系统的属性特点，所以，选用它作为分析动态人体行为的一个特征.K￣S熵(HKS)是在单位时间趋向∞并且盒子大小趋向0的条件限制下的平均熵，即

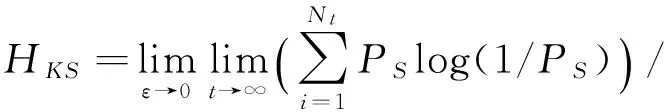
综上所述，人体行为的每条轨迹可以用一个融合了上述这些不变量的3维特征向量(C,λ1,HKS)表示，每个参考关节点可以由一个9维的特征向量表示，每个动作可以用一个90维的特征向量表示.

3 基于RVM的行为识别

相关向量机(Relevance Vector Machine,RVM)[17]是TIPPING M E于2001年在贝叶斯框架的基础上提出的，它有与支持向量机(Support Vector Machine,SVM)一样的函数形式，与SVM一样基于核函数映射将低维空间非线性问题转化为高维空间的线性问题.

为了在L类分类问题中用到RVM，需要训练一些(L)RVMs，每个都能从一些其他人体行为中将某一类行文分离出来.给定数据样本X，给每个(L)RVMs一个X属于每个L类的概率，从而数据样本被划分到具有最大概率的某一类.

给定一个有N个输入目标对的训练数据集{Xn,ln}(1 ≤n≤N)，RVM学习权值w={w1,…,wn}，条件概率P(l|w,X)用于预测一个数据样本X的标签l，学习的过程采用最大后验概率估计方法，具体过程如下：(1)条件概率P(l|w,F)相应进行建模；(2)先验概率P(w|a)确保权值向量w是稀疏的.

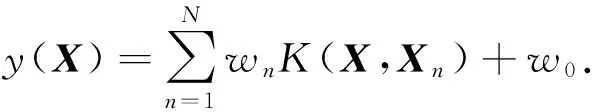
P(l|w,X)=f{y(X)}l(1-f{y(X)})1-l，

在2类问题的分类过程中，通过使条件概率P(l|X)最大，样本X被分到类l∈ [0,1].为了在多类问题中使用RVM分类器，对每个类训练一个分类器，即L个不同的类就训练L个不同的分类器，于是给定的样本X被分类到条件概率Pi(l|X)( 1 ≤i≤L)最大的某一个类为Class(X)=arg max(Pi(l|X)).

4 实验

实验分别采用3个数据集：KTH人体行为数据集、Weizmann人体行为数据集和ballet数据集.

KTH人体行为数据集里含有6种人体动作(走、慢跑、快跑、拳击、挥舞手以及鼓掌)，这6种动作分别由25个主体在4种不同场景中做出相应动作几次组成，其中4种场景包含室外场景、具有规模变化的室外场景、不同穿着的室外场景以及室内场景.这些数据集的代表帧如图5a)所示.初始化输入是10个参考点轨迹的形式以及所有在文中第1部分涉及的数量级的时间序列，所以每个参考结点用3个时间序列(x,y,z)表示,每个动作用30个时间序列表示.每条时间序列通过嵌入重构相空间最后计算得出最大李雅普诺夫指数、相关积分和Kolmogorov￣Sinai熵，从而融合这3种特征后得到一个90维的特征向量.当使用RVM分类器，用新方法对KTH数据集的识别结果如表1所示，整个数据集的平均正确率相比文献[8]中89.7%的平均正确率，此次达到91.2%.

图5表示每个数据集的行为分别代表KTH数据集、Weizmann数据集、ballet数据集，而ballet数据集中动作分别为从左到右打开手、从右到左打开手、站立着打开手、摆动腿、跳跃、转弯、单脚跳、静立.

图5 数据集的逐帧采样

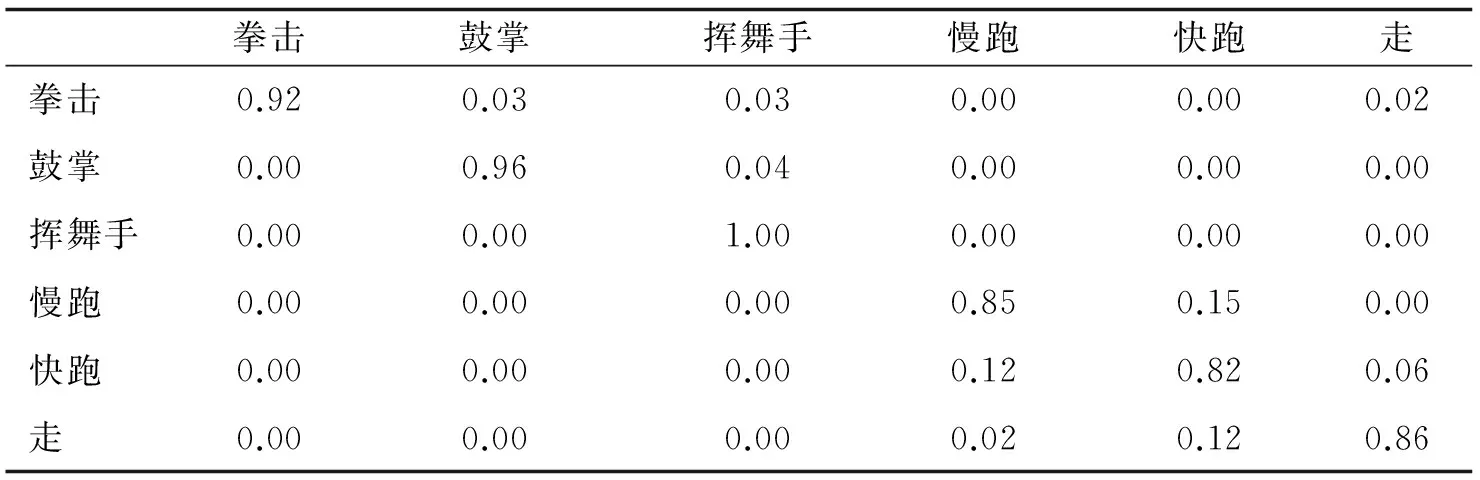
表1 对于KTH数据集的混合矩阵

Weizmann人体行为数据集包含9个不同的人展示9种不同的动作组成的83个视频序列.9种不同的动作包括跑、走路、跳跃、两腿向前跳、两腿原地向上跳、侧面急速前行、双手挥舞、单手挥舞以及弯腰.文中的数据使用背景相减法对数据集追踪和定位而得到.一些样本帧如图5b所示.通过新方法分类得到的结果如表2所示，相比文献[8]中算法得到的平均正确率90.6%，使用新方法对整个测试数据集可以达到93.3%.

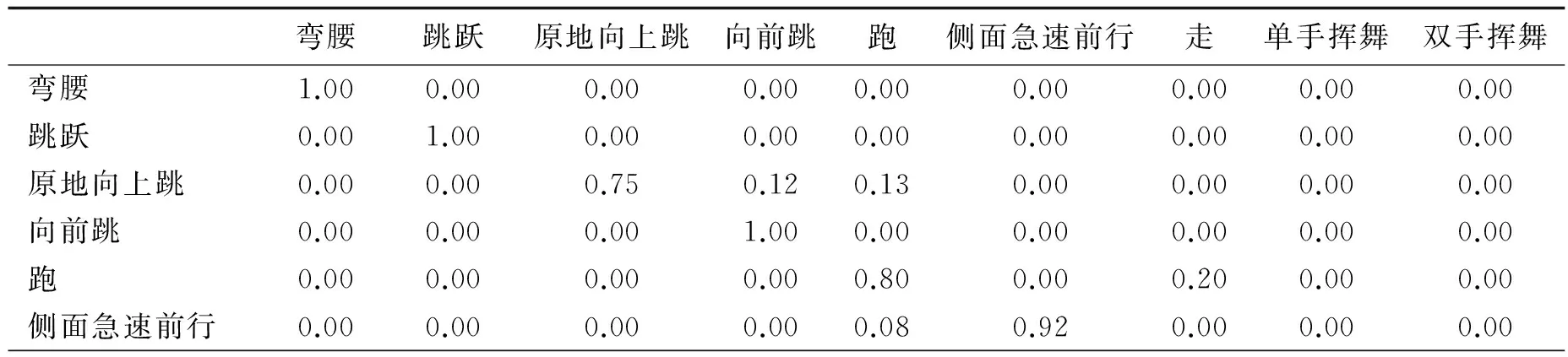
表2 对于Weizmann数据集的混合矩阵

续表

最后，对从芭蕾教学DVD视频中收集的ballet数据集用新方法进行测试.这个数据集在文献[18]中使用.图5c)示出一些样本帧，表3示出使用新方法得到的分类结果.对ballet数据集每一帧比较，用文献[18]的方法得到数据集准确率达51%，而用新方法可以达到91.8%.由于文献[18]中实验采用同样的实验设置，因此结果相对比较公平.

表3 对于ballet数据集的混合矩阵

实验结果表明，新方法与文献[8，18]中所用方法相比，更有明显的优点，能够得到更加满意的平均准确率.新方法能够从小数据集准确地计算出最大李雅普诺夫指数，而且使用Kolmogorov￣Sinai熵能更好地反映更多的动态系统的混沌特性.

5 结语

(1)提出了一种人体行为的非线性动力学系统特征化的方法，动力学系统的奇异吸引子的混沌不变量特征被提取出来，如最大李雅普诺夫指数、相关积分和Kolmogorov￣Sinai熵.

(2)行为识别使用RVM算法和混沌不变量特征.文中用于行为识别的方法经过KTH和Weizmann人体行为数据集测试，证明有明显的可行性和潜在优点.

(3)实验结果表明，新方法比较真实有效，平均正确率在KTH、Weizmann及ballet数据集上分别达到了91.2%，93.3%和91.8%，明显比文献[8]中的89.7%，90.6%和51%更高；同时，使用新方法对整个数据集的平均正确率与文献[18]中方法相比可以达到92.1%.

[1] JHUANG.H,SERRE T,WOLF L,et al.Biologically Inspired System for Action Recognition[C].Proceedings of IEEE 11th International Conference.Taichung,Taiwan:ICCV,2007:342-346.

[2] SCHINDLER K,VAN G L.Action Snippets:How Many Frames Does Action Recognition Require?[C].Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Anchorage,Alaska,USA:CVPR,2008:1 121-1 127.

[3] IKIZLER N,FORSYTH D.Searching Video for Complex Activities with Finite State Models[C].Proceedings of IEEE Conf. Computer Vision and Pattern Recognition.Minneapolis,MN,USA:CVPR,2007:489-496.

[4] LAXTON B,LIM J,KRIEEGMAN L D.Temporal Contextual and Ordering Constraints for Recognizing Complex Activities in Video[C].Proceedings of IEEE Conf. Computer Vision and Pattern Recognition.Minneapolis,MN USA:CVPR,2007:298-306.

[5] LAPTV I,LINDEBER T.Space￣Time Interest Points[C].Proceedings of Ninth IEEE International Conf. on Computer Vision.Nice,France:ICCV,2003:432-439.

[6] LIU Jingen,MUBARAK SHAH.Learning Human Actions via Information Maximization[C].Proceedings of IEEE Conf. on Computer Vision and Pattern Recognition.Anchorage,AK,USA:CVPR,2008:812-819.

[7] NIEBLES J C,LI Feifei.A Hierarchical Model of Shape and Appearance for Human Action Classification[C].Proceedings of IEEE Conf. on Computer Vision and Pattern Recognition Minneapolis.MN USA:CVPR,2007:65-73.

[8] ALE S,BASHARAT A,SHAH M.Chaotic Invariants for Human Action Recognition[C].Proceedings of IEEE Computer Vision and Pattern Recognition.Rio de Janeiro,Brazil:ICCV,2007:290-298.

[9] GONG Wenjuan,ANDREW D,BAGDANOV F,et al.Automatic Key Pose Selection for 3D Human Action Recognition[J].Computer Science,2010,61(6):290-299.

[10] REN Haibing,XU Guangyou.Articulated￣Model Based Upper￣Limb Pose Estimation[C].Proceedings of IEEE International Symposium on Computational Intelligence in Robotics and Automation.Aanff,Alberta,Canada:CIRA,2001:450-454.

[11] XU Feng,KIN M L,DAI Qinghai.Video￣Object Segmentation and 3D￣Trajectory Estimation for Monocular Video Sequences[J].Image and Vision Computing,2011,29(1):190-205.

[12] PACKAR N H,CRUTCHFIELD J P,FARMER J D,et al.Geometry from a Time Series[J].Phys. Rev. Lett.,1980,45(9):712-716.

[13] KIM H S,EYKHOLT R,SALAS J D.Nonlinear Dynamics,Delay Times,and Embedding Windows[J].Physica D:Nonlinear Phenomena,1999,127(1):48-60.

[14] GRASSBERGER P.Grassberger￣Procaccia Algorithm[J].Scholarpedia,2007,2(5):3 043-3 044.

[15] LI Xibing,WANG Qisheng,YAO Jinrui,et al.Time Series Prediction for Surrounding Rock’s Deformation of Mine Lanes in Soft Rock[J].Journal of Central South University of Technology,2008,15(2):224-229.

[16] ROSENSTEIN M T,COLLINS J J,LUCA D C J.A Practical Method for Calculating Largest Lyapunov Exponents from Small Data Sets[J].Physica D,1993,65(1):117-134.

[17] TIPPING M E.Sparse Bayesian Learning and the Relevance Vector Machine[J].Journal of Machine Learning Research,2001,1(6):211-244.

[18] FATHI A,GREG MORI.Action Recognition by Learning Mid￣Level Motion Features[C].Proceedings of IEEE CS Conf. Computer Vision and Pattern Recognition.Anchorage,AK,USA:CVPR,2008:311-317.

(责任编辑 向阳洁)

RecognitionofHumanBehaviorBasedonChaosInvariantandRelevanceVectorMachine

DAI Zhiqiang,DONG Jianfeng

(College of Tourism and Management Engineering,Jishou University,Zhangjiajie 427000,Hunan China)

An algorithm is put forward for the recognition of human behavior based on chaos invariant characteristics and relevance vector machine(RVM).First,the motion track generated by the joints of human is extracted to represent the nonlinear system of human movement behavior and C￣C method is used to estimate the delay to obtain the dimension of phase space reconstituted by every motion track.Furthermore,the chaos invariant which represents human behavior is extracted from the phase space and RVM algorithm is used to recognize human behavior.Finally KTH,Weizmann human behavior database and ballet database are applied to test the effect of the algorithm,and the result proves that this method has the better recognition effect than others.

chaos system;behavior recognition;chaos invariant;RVM

1007-2985(2014)03-0037-07

2014-03-20

吉首大学校级科研课题(13JD031)

戴志强(1981-)，男，湖南邵阳人，吉首大学旅游与管理工程学院讲师，中南大学硕士，主要从事计算机应用技术研究.

A

10.3969/j.issn.1007-2985.2014.03.009